



摘" 要:金融市场预测通常被认为是数据挖掘中最具挑战性的任务之一。最近Transformer模型在提高金融时序预测(Financial Time-Series Forecasting, FTSF)的精度方面取得了成功,但由于作为隐含的复杂信息,且可用的标记数据较少,当前基准在该领域的泛化能力较差。为缓解干净数据不足导致的过拟合问题,提出一种Transformer结合对抗域适应的深度迁移学习框架TADA-FTSF,用于金融领域TSF任务,以提高深度预测模型的可靠性与准确性。
关键词:金融时序预测;Transformer模型;域适应;迁移学习
中图分类号:TP183;TP39" 文献标识码:A" 文章编号:2096-4706(2024)24-0140-07
A Transfer Learning Method Based on Transformer and Its Application in Financial Time-Series Forecasting
WANG Yang
(China UnionPay Big Data Division, Shanghai" 201201, China)
Abstract: Financial market forecasting is generally considered to be one of the most challenging tasks in data mining. Transformer model has recently been successful in improving the accuracy of Financial Time-Series Forecasting (FTSF). However, due to the complex information as implicit and the small amount of labeled data available, current benchmarks have poor generalization ability in this field. In order to alleviate the overfitting problem caused by the lack of clean data, a deep Transfer Learning framework named TADA-FTSF which combines with Transformer and adversarial domain adaptation is proposed for TSF tasks in the financial field, to improve the reliability and accuracy of the deep forecasting model.
Keywords: Financial Time-Series Forecasting; Transformer model; domain adaptation; Transfer Learning
0" 引" 言
时序预测的目的是使用一个模型,根据描述历史序列变量的变化Xi={x1,x2,…,xt}来预测未来的变化,其中Xi表示第i个变量,t表示时间观测的长度。金融时序预测是一个高度相关的研究领域,在管理风险、正确决策和实现金融目标方面起到至关重要的作用。
金融时序预测具有较强的非线性,并且数据规模较大。因此,传统的时序预测方法(例如自回归(AR)[1]、自回归综合移动平均(ARIMA)[2]和指数平滑(ETS)[3])受限于其线性预测特点,难以完成用于金融时序预测任务。
近年来,深度学习在多个计算机领域里表现出了极具竞争力的性能[4]。许多深度学习模型,如长短期记忆网络(LSTM)[5]、门控循环单元(GRU)[6]和时间卷积网络(TCN)[7],已经被应用于时间序列预测任务[8-9]。与传统方法相比,深度学习模型的非线性拟合能力更适用于大规模的金融时序预测任务。
相比于常规的时序数据,金融时序序列采样时间固定并且持续性长。同时,其数值波动受多种因素影响,从而导致对金融数据的建模需要同时考虑长程性与鲁棒性[10]。为了解决这一问题本文基于RSA-Transformer,提出了一种基于迁移学习的金融时序预测方法,称为TADA-FTSF。针对金融数据建模的长程性,RSA-Transformer有效地克服了长程建模中的大计算量与参数量,并利用残差结构保证了长时建模过程中的梯度传递;针对金融数据建模的鲁棒性,TADA-FTSF基于源域数据集指导目标域数据,完成金融时序预测。一方面能够减少数据不足给模型训练带来的负面影响。另一方面,跨域学习能够减少噪声对模型的干扰,从而提升预测结果的鲁棒性。
本文对提出的TADA-FTSF架构进行大量实验,实验结果证明了本文提出框架的有效性与鲁棒性。
1" 相关研究工作
1.1" 金融TSF的深度学习模型
预测整个金融市场通常被视为时间序列预测任务,可分为传统线性预测技术和非线性预测技术。由于统计学原理的局限性,引入深度神经网络等智能模型。深度学习模型在机器学习领域取得了突出表现,包括时间序列预测。将LSTM、GRU、TCN等应用于TSF任务,展现了优秀的非平稳建模能力。例如,Zhang利用LSTM进行股票指数预测,取得了良好结果[11]。Li和Wang提出了ST-GRU模型,提高了能源期货价格的预测精度[12]。Lei结合TCN和百度搜索索引进行波动预测[13]。尽管深度学习模型在捕获金融时间序列中的非线性模式方面表现出色,但由于样本效率低,容易出现过拟合。因此,为了增强金融时间序列的可预测性,迁移学习是必要的。
1.2" 金融TSF的迁移学习
迁移学习是机器学习的一个重要分支,致力于将已学知识应用于新领域,以提高解决新问题的能力和速度。在时间序列挖掘任务中,迁移学习展现出良好泛化性能[14]。例如,Ye和Dai提出了RATL算法,用于汇率预测,分为表示关系对齐和回归关系对齐两个阶段[15]。Nguyen和Yoon提出了DTRSI框架,通过对LSTM进行预训练和微调,优化股价预测性能[16]。He等人提出了基于两个源数据集的迁移学习训练策略,使用DTW衡量时间序列相似性以选择源域[17]。这些方法在金融时间序列预测中取得成功,克服了单源迁移学习的限制。虽然这些方法推动了时间序列分析领域的发展,但与ADA-FTSF框架存在显著差异。ADA-FTSF在预训练阶段使用域适应来减少源域和目标域的分布和特征差异,仅使用单源迁移学习取得良好性能,且是模型无关的,无须指定应用场景。
2" TADA-FTSF框架
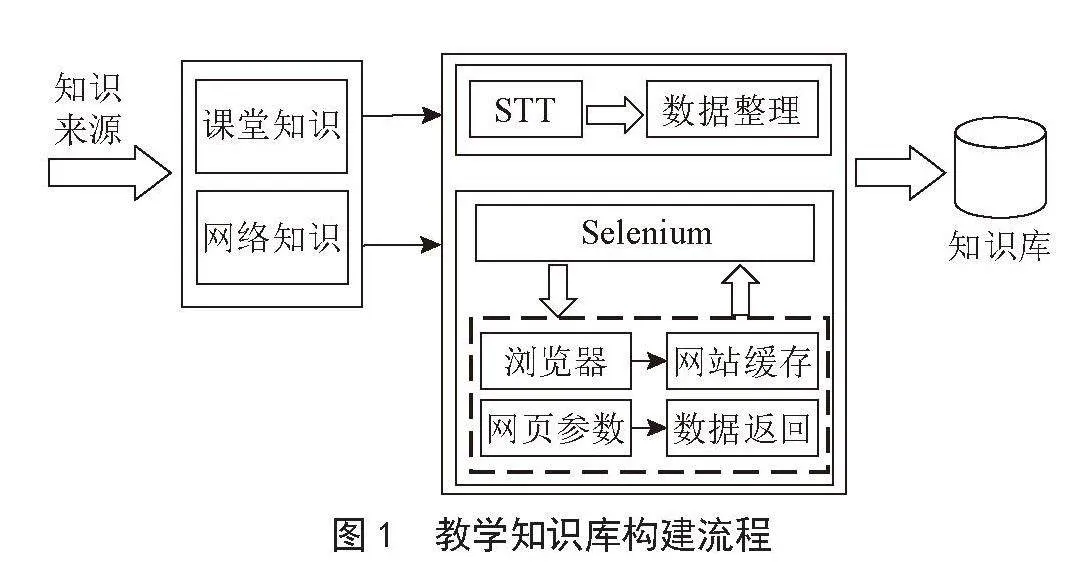
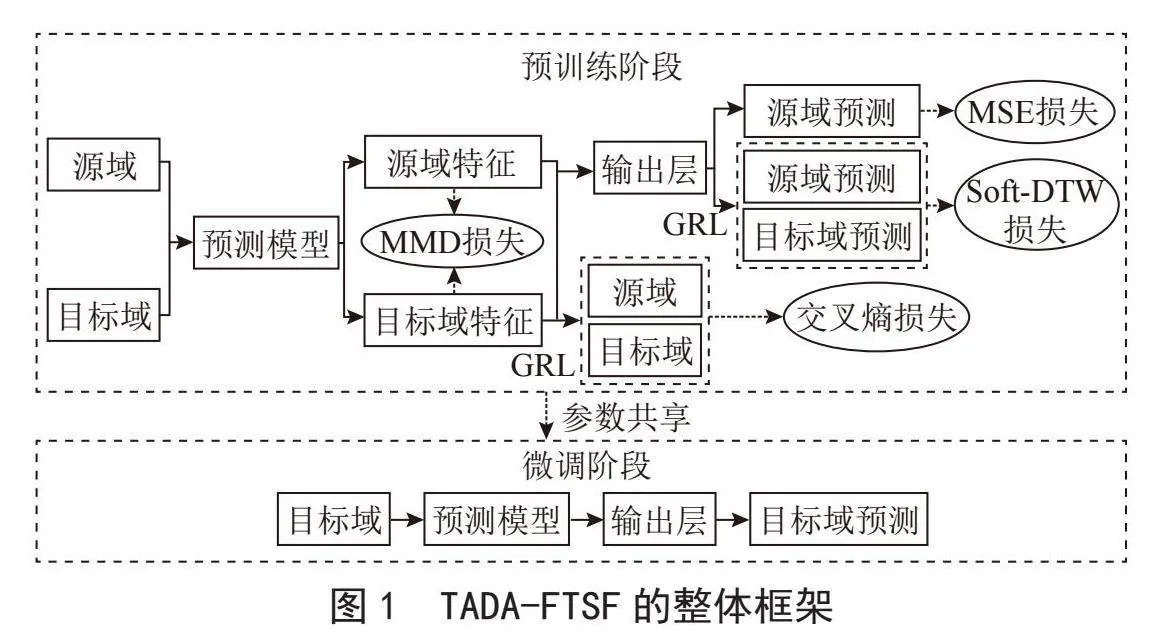
在本节中,对我们提出的框架进行合理的介绍,其训练流程如图1所示。本节首先提供了一个选择源数据集的新视角。然后,详细描述了TADA-FTSF框架包含的组件以及训练损失函数。
2.1" 面向潜在源域选择的时序因果关系发现
在迁移学习任务中,源数据集的选择在很大程度上影响了知识的迁移效果,传统方法通常依赖于耗时的人工选择或者训练大量数据集得到多种预训练模型。为了解决这一问题,本节提出了一种新的时序因果发现方法,为FTSF迁移学习任务中的源域选择提供了新的视角。
因果关系在自然界中普遍存在,因果关系的发现是交叉学科的主要命题之一。时序因果发现可以阐述发现时间序列之间的因果关系,是统计学中时间序列分析的一个经典问题,在各种领域中具有重要的应用价值。传递熵(Transfer Entropy, TE)是衡量因果关系的常用度量之一,它测量了从一个变量传递到另一个变量的信息量,具有模型不可知和不假设数据分布的优点[18]。两个序列间的TE计算方式如下:
(1)
其中,Xi,Yi,i = 1,2,…,T与Y i=(Y1,…,YT)为两个不同的时间序列。Ma提出了Copula熵的概念,并且证明了它等价于信息论中的互信息[19]。设x为随机变量,其边缘分布为u,Copula密度为c(u)。x的Copula熵计算如下:
(2)
Copula熵是独立性的度量,而TE是条件独立性的度量。文献[20]介绍了存在一个基本的理论关联。传递熵可以只能用Copula熵表示,如下所示:
(3)
在本文方法中,根据式(3)来通过Copula熵计算从源数据集的每个变量到目标数据集的目标变量的平均TE。选择具有最大TE的源数据集作为源域。
2.2" TADA-FTSF组件分析
2.2.1" RSA-Transformer模型
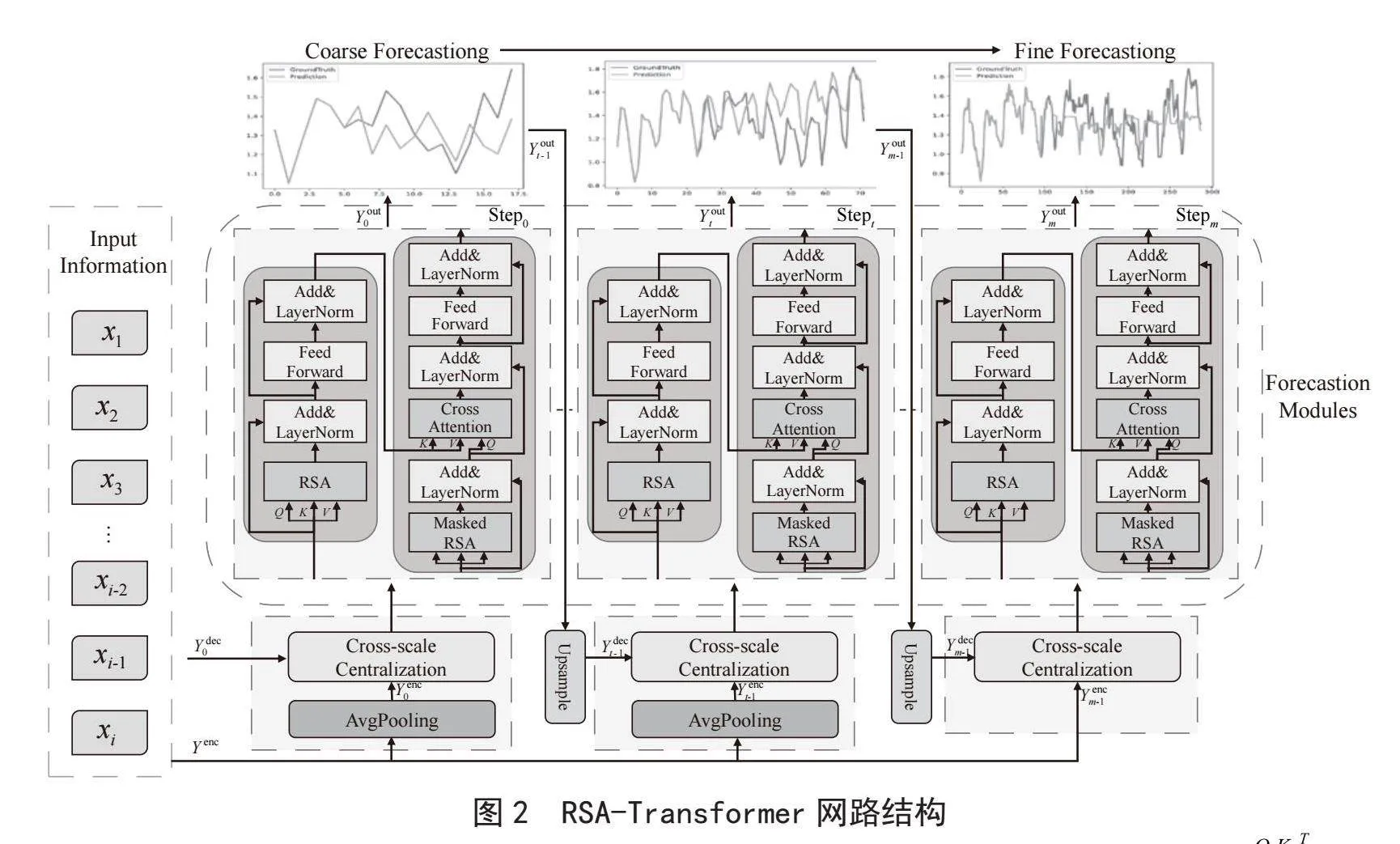
由于良好的长程依赖性和交互建模能力,Transformer已被用于解决长序列时间序列预测问题。然而,标准的自注意力机制具有压倒性的二次计算复杂性和高内存使用问题。此外,不相关和冗余信息也会对预测的有效性产生影响。单尺度预测使得模型缺乏在不同时间尺度上提取序列时间模式的能力。为应对这些挑战,RSA-Transformer以一种基于多尺度的高效框架来处理FTSF任务。网络结构如图2所示。
标准的Transformer由键(Key)向量k,值(Value)向量v和查询(Querry)向量q组成,通过计算q和k之间的相似度,并随后根据相似度的大小为v分配不同的权重,流程可以表达为:
(4)
其中,Q,K,V分别为由向量q,k,v构成的数组。sim()为Q与K之间的相似性度量,其在标准自注意力机制中的尺度点积运算为:
(5)
其中,,,,d为输入维度。与神经网络的自回归方法不同,自注意力机制的每个计算不依赖于前一个的结果,从而导致高度并行。基于注意力矩阵的稀疏性准则,利用文献[21]提出的查询稀疏性度量,将第i个Q对第j个K的关注度定义为概率P(KjQi)。主导点积对使得响应Q的关注度概率分布偏离均匀分布M(KjQi)=1/LK。如果P(KjQi)接近均匀分布,则可以认为注意力区域是无关信息,可以直接忽略。我们用K-L散度来衡量两个概率分布P和M之间的差异:
(6)
忽略lnLK常数项,第i个查询的稀疏度指标可以定义为:
(7)
其中第1项是第i个查询和所有键的对数和展开运算,而第2项是它们的算术平均值。然而,这样的计算仍然需要消耗O(L2)内存,而且对数和展开运算还有潜在的数字稳定性问题。当很大时,会溢出,当都很小时,接近于0,则ln的计算也会引起数值问题。因此,我们采用一个近似的查询稀疏性度量表示如下:
(8)
基于此,本文的稀疏注意力机制可以表示为:
(9)
其残差结构为:
(10)
RSA-Transformer的原始输入序列在嵌入层经过一系列编码后,通过编码器-解码器框架进行处理。利用RSA机制降低计算复杂度,优化模型预测性能。
2.2.2" 构造混合损失函数
在TADA-FTSF框架中,本文为预训练阶段设计了一种混合损失函数,由4部分组成用于对齐源域和目标域分布,具体阐述如下:
(11)
L1表示在原数据上的MSE损失,计算如下:
(12)
其中,Ns表示带标签的源域,f(xi)为特征提取网络,本文中采用的是RSA-Transformer。
L2为最大均值差异(Maximum Mean Discrepancy, MMD)损失[22],MMD是基于分布的域适应中最常用的特征距离度量,它试图探索两个给定样本是否属于相同的分布,并定义两个样本分布之间的距离和均值嵌入特征之间的距离。具体计算如下:
(13)
L3为对抗损失。学习域不变特征的假设是,在一个训练好的域分类器中,不同域上的特征是不可区分的。为了实现这一目标,负信号Rλ用于表示梯度反转层(Gradient Reversal Layers, GRL)。网络训练前后的目标是达到对抗训练的效果,使特征提取层提取到更鲁棒的特征,从而使预测层能够预测目标域。本质上,域判别器的准确性描述了两个数据域的边缘分布的差异,然后,特征生成器的目标是尝试使用域鉴别器,从而减少边缘分布的差异。L3具体计算如下:
(14)
L4为soft-DTW损失。为使预测结果更好地匹配实际情况。DTW[23]利用动态编程在时间轴上进行局部缩放,使不同两个序列的形态一致成为可能。然而,作为一个独立函数,由于最小操作的不可微性,DTW对于其输入是不可微的。文献[24]提出了一种可微扩展,用soft-min代替min过程。因此,soft-DTW依赖于控制结果度量的平滑性的超参数γ。在本文迁移学习过程中,为了使预训练集源域的预测误差在预训练期间更小,添加GRL以产生上述的对抗性效应。L4随后降低了神经网络调优的负担,导致形状知识[25]的迁移,具体计算如下:
(15)
深度神经网络的训练过程主要包括前向传播和后向传播。在反向传播过程中,需要求解网络参数的梯度。然后,利用梯度下降法找到最优网络参数;采用AdamW算法来解决优化问题[25]。
3" 实验结果
3.1" 实验数据集
本文实验是聚集采用从国际知名金融网站(https://www.investing.com/)上收集的金融指数序列数据,包括上证综合指数(SHI)、深证成指(SZI)、道琼斯工业平均指数(DJI)、标准普尔500指数(SP)、香港恒生指数(HSI)和纳斯达克综合指数(NCI)。
数据从2010年1月5日至2023年12月31日,日粒度收集。由于交易周期不同,数据规模未对齐。在迁移学习中,本文不能泄露未来信息,因此对所有时间序列进行了数据扩展和线性插值填充,以实现数据尺度对齐。每个目标数据集按时间分为80%训练和20%测试。本文选择四个变量,如开盘价、最高价等,利用向量自回归模型(VAR),根据BIC准则选择滞后周期,并将其转换为适合监督学习问题的输入。
3.2" 实验设置
在实验中,为了说明本文迁移学习框架以及RSA-Transformer模型的有效性,本文选择了一些有竞争力的基准方法作为对比,包括原始LSTM、原始TCN、原始GRU、支持向量回归(SVR)和随机森林(RF)。同时,为了更好地评估所提出框架的性能,本文还将提出的迁移学习框架分别应用于TCN、LSTM和GRU,即ADA-TCN、ADA-LSTM和ADA-GRU。在这些模型的详细设计中,ADA-LSTM和ADA-GRU分别堆叠了两层LSTM层和两层GRU层作为特征提取模块。而ADA-TCN堆叠了四层,被称为因果卷积块。这三个模型都包含了一个全连接层作为预测模块。
由于TADA-FTSF利用了源域到目标域的知识,为了更好地评估实验结果,使其更具可比性,在原始模型中使用了典型的迁移学习策略进行对比。该策略首先在源域上进行预训练,然后在目标域上进行微调。这些模型被简称为TL-LSTM、TL-TCN和TL-GRU。
根据大量实验结果,将ADA-LSTM、ADA-GRU和ADA-TCN的超参数设置为k1 = k2 = 1,k3 = 0.1。根据预测误差从{16,32,64}中选择每层的最佳隐层大小。在训练过程中,根据训练损失自适应调整学习率。初始学习率设置为0.1,最小学习率设置为0.000 000 1。一旦训练损失在5个Epoch内不再下降,学习率就降低到自身的四分之三。为了完全训练模型,将迭代次数设置为10 000次。此外,传统的机器学习模型如SVR和RF使用随机搜索来优化参数。
数据归一化旨在将预处理后的数据限制在一定范围内,消除单一样本数据带来的不利影响。我们采用最小-最大归一化方法调整变量的维数。同时,作为评价标准,本文计算了均方根误差(RMSE)和对称平均绝对百分比误差(sMAPE),具体计算方式如下:
(16)
(17)
3.3" 对比实验
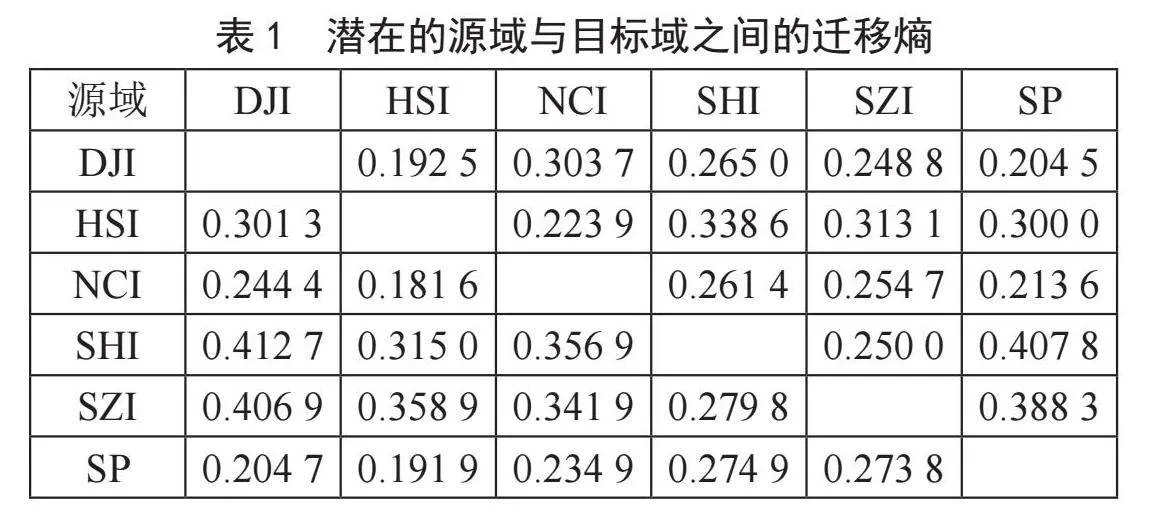
本节首先通过传递熵选择了适当的源域。将每个数据集分别视为目标域,而其余数据集则被视为潜在的源域。根据计算出的基于转移熵的因果关系,我们在表1中用粗体表示了传递熵最大的数据集,并选择其作为源域。通过分析表1,我们得知对应的源域为NCI、SHI、SHI、DJI、DJI和SHI。
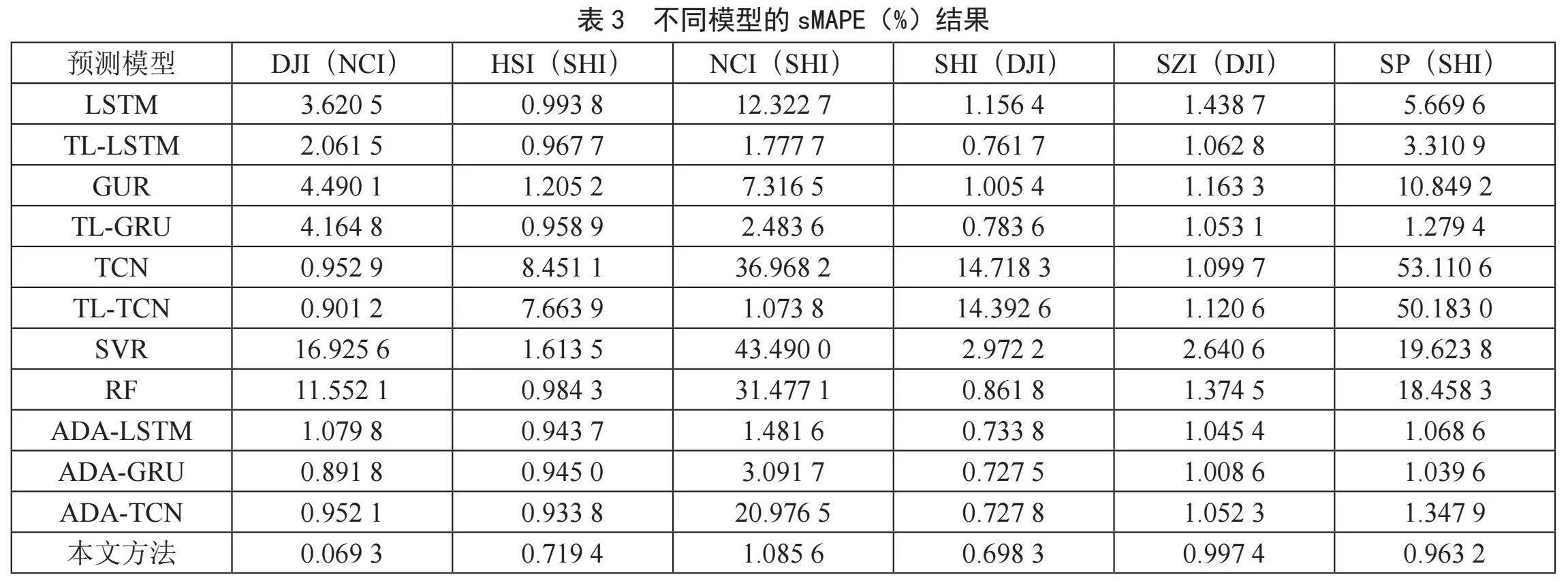
本节还统计了预测财务指标数据集的RMSE和sMAPE值,如表2和表3所示。值得注意的是,最低的RMSE和sMAPE值用粗体标记,而加下划线表示所提出的框架提高了原始模型的性能。通过对表2和表3的分析,我们发现本文的相比于ADA-的方法,本文的TADA-FTSF取得了最佳的性能,这说明了本文采用的RSA-Transformer模型对金融数据的适应性更好。
同时,通过观察可以发现,ADA-的方法在绝大多数情况下都取得了比原始方法以及基于微调的TL-方法,这说明了本文提出的迁移学习框架的有效性。
还有一些细节需要注意。ADA-TCN的性能非常不稳定,可能是由于其复杂的结构导致网络训练困难。然而,我们使用的数据集相对较小,TCN模型更适用于大数据。此外,我们使用的大多数时间序列数据集都不是平稳的。实验结果验证了所提框架在非平稳条件下的建模能力,展示了其端到端的特性。
3.4" 消融研究
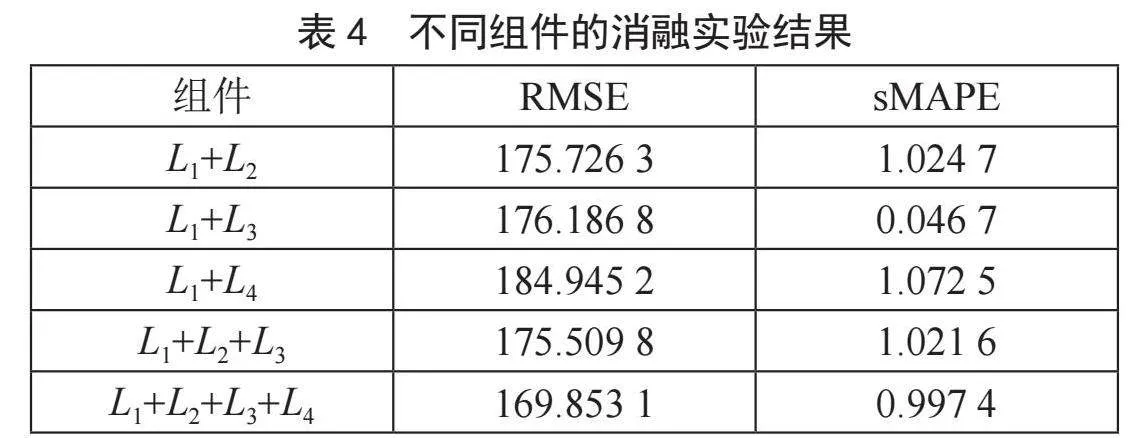
本节进行了TADA-FTSF框架的消融实验(针对4个损失函数对应的组件)以验证每个组件的有效性。由于篇幅有限,本文仅在SZI上对TADA-FTSF进行消融研究。结果表明,添加任何新的基于迁移的组件都比从头开始训练模型的性能更好。L1+L4对SZI产生了负迁移作用,可能是因为数据集的值范围发生了变化。混合损失函数显示了具有竞争力的性能,其中L4的强耦合能力提高了整体性能,负面影响相互抵消,达到更好的泛化平衡。不同组件的消融实验结果如表4所示。
3.5" DM检验结果
DM检验用于比较两个模型之间的预测效果,本质上就是t检验。在假设检验中,零假设表示两个模型的预测误差没有差异,备择假设表示两个模型的预测误差不同。假设目标模型A的预测精度与基准模型B的预测精度相等,则原假设可以表述为:
(16)
其中,与分别为模型A和B的预测误差,损失函数F为均方误差,DM statistic可以根据下述公式计算:
(17)
其中,,
并且,。γ0为gt的方差;xA,t和xB,t分别为模型A和模型B在周期t的预测。T为测试集上的观测数。
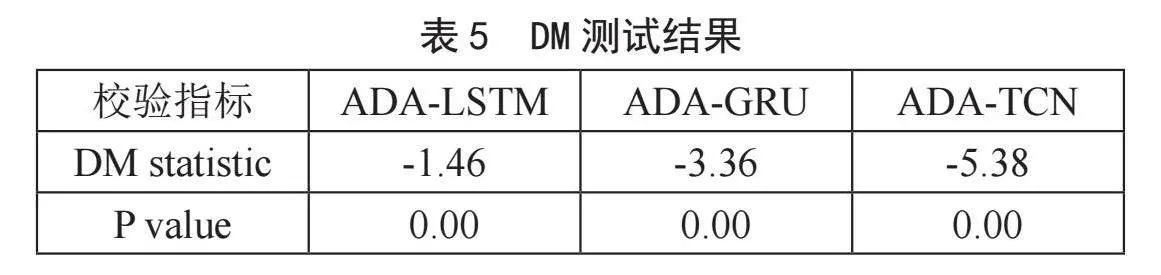
为了节省空间,本节使用DM测试对TADA-FTSF的框架进行了分析,即TL-LSTM vs ADA-LSTM、TL-GRU vs ADA-GRU、TL-TCN vs ADA-TCN。上述三个数据集的近似结果如表5所示。显然,在SZI上,这三种情况均以几乎100%的置信度通过显著性检验,表明所提出的框架的实用性与可靠性。
4" 结" 论
本文提出的TADA-FTSF框架致力于解决金融时间序列的高精度预测难题。其创新主要包括三个阶段:首先,针对金融数据的长时性,利用RSA-Transformer作为特征提取器,使特征对金融数据的拟合更好。其次,结合时序因果发现,通过计算时间序列的迁移熵选择源域,该方法不仅满足信息不泄露的要求,还比传统方法更简单可解释。最后,采用对抗域适应策略,利用soft-DTW损失函数引入形状知识,提高框架的泛化能力。实验结果显示,该框架在金融时间序列上具有良好的预测性能和泛化能力。未来的工作可以探索基于统计相似度的源域选择效果,解决多源域迁移中的错误源域选择问题,以进一步完善该框架。
参考文献:
[1] JANACEK G. Time Series Analysis Forecasting and Control [J/OL].Journal of Time Series Analysis,2010:(2010-06-08).https://doi.org/10.1111/j.1467-9892.2009.00643.x.
[2] LEE Y S ,TONG L I. Forecasting Time Series Using a Methodology based on Autoregressive Integrated Moving Average and Genetic Programming [J].Knowledge-Based Systems,2011,24(1):66-72.
[3] CORBERÁN-VALLET A,BERMÚDEZ J D,VERCHER E. Forecasting Correlated Time Series with Exponential Smoothing Models [J].International Journal of Forecasting,2011,27(2):252-265.
[4] LECUN Y,BENGIO Y,HINTON G. Deep Learning [J].Nature,2015,521(7553):436-444.
[5] FISCHER T ,KRAUSS C .Deep Learning with Long Short-Term Memory Networks for Financial Market Predictions [J].European Journal of Operational Research,2017,270(2):654-669.
[6] ARYAL S,NADARAJAH D,RUPASINGHE P L,et al. Comparative Analysis of Deep Learning Models for Multi-Step Prediction of Financial Time Series [J].Journal of Computer Science,2020,16(10):1401-1416.
[7] SEZER O B,GUDELEK M,UOZBAYOGLU A M. Financial Time Series Forecasting with Deep Learning: A Systematic Literature Review: 2005-2019 [J/OL].Applied Soft Computing,2020,90:106181(2020-02-25).https://doi.org/10.1016/j.asoc.2020.106181.
[8] LI A W ,BASTOS G S .Stock Market Forecasting Using Deep Learning and Technical Analysis: A Systematic Review [J].IEEE Access,2022,8:185232-185242.
[9] NIU T ,WANG J Z,LU H Y,et al. Developing a Deep Learning Framework With Two-Stage Feature Selection for Multivariate Financial Time Series Forecasting [J/OL].Expert Systems with Applications,2020,148(C):(2020-06-15).https://doi.org/10.1016/j.eswa.2020.113237.
[10] LI G,ZHANG A,ZHANG Q,et al. Pearson Correlation Coefficient-based Performance Enhancement of Broad Learning System for Stock Price Prediction [J].IEEE Trans Circ Syst II Express Briefs,2022,69(5):2413-2417.
[11] ZHANG Y,YAN B,AASMA M.A Novel Deep Learning Framework: Prediction and Analysis of Financial Time Series using CEEMD and LSTM [J/OL].Expert Systems with Applications,2023:113609(2020-11-30).https://doi.org/10.1016/j.eswa.2020.113609.
[12] LI J,WANG J. Forcasting of Energy Futures Market and Synchronization based on Stochastic Gated Recurrent Unit Model [J/OL].Energy,2023,213:118787(2020-12-15).https://doi.org/10.1016/j.energy.2020.118787.
[13] LEI B,ZHANG B,SONG Y. Volatility Forecasting for High-Frequency Financial Data Based on Web Search Index and Deep Learning Model [J/OL]. Mathematics,2023,9(4):320(2021-02-05).https://doi.org/10.3390/math9040320.
[14] LAPTEV N. Reconstruction and Regression Loss for Time-Series Transfer Learning [C]//24th ACM SIGKDD Conference on Knowledge Discovery and Data Mining.London:ACM,2018:1-8.
[15] YE R,DAI Q. A Relationship-Aligned Transfer Learning Algorithm for Time Series Forecasting [J].Information Sciences,2022,593:17–34.
[16] NGUYEN T T,YOON S. A Novel Approach to Short-Term Stock Price Movement Prediction Using Transfer Learning [J/OL].Applied Sciences,2023,9(22):4745(2019-11-07).https://doi.org/10.3390/app9224745.
[17] HE Q Q,PANG P C I,SI Y W. Transfer Learning for Financial Time Series Forecasting [C]//PRICAI 2023:Trends in Artificial Intelligence:16th Pacific Rim International Conference on Artificial Intelligence.Fiji:Springer,2023:24-36.
[18] RUNGE J,BATHIANY S,BOLLT E,et al. Inferring Causation from Time Series in Earth System Sciences [J/OL].Nature Communications,2019,10(1):2553(2019-06-14).https://www.nature.com/articles/s41467-019-10105-3.
[19] REID A T,HEADLEY D B,MILL R D,et al. Advancing Functional Connectivity Research From Association to Causation [J].Nature Neuroscience,2019,22(11):1751-1760.
[20] SACHS K,PEREZ O,PEER D,et al. Causal Protein-Signaling Networks Derived from Multiparameter Single-Cell Data [J].Science,2005,308(5721):523-529.
[21] YIN X ,ZENG J ,HOU T ,et al. RSAFormer: A Method of Polyp Segmentation with Region Self-Attention Transformer [J/OL].Computers in Biology and Medicine,2024,108268(2024-04-16).https://doi.org/10.1016/j.compbiomed.2024.108268.
[22] SMOLA A,GRETTON A,SONG L,et al. A Hilbert Space Embedding for Distributions [C]//Algorithmic Learning Theory:18th International Conference.Sendai:Springer,2007:13-31.
[23] SAKOE H,CHIBA S. Dynamic Programming Algorithm Optimization for Spoken Word Recognition [J].IEEE Trans Acoust Speech Signal Process,1978,26(1):43-49.
[24] CUTURI M,BLONDEL M. Soft-DTW: A Differentiable Loss Function for Time-Series [C]//Proceedings of the 34th International Conference on Machine Learning (ICML).JMLR,2017:894-903.
[25] LE GUEN V,THOME N. Deep Time Series Forecasting with Shape and Temporal Criteria [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2022,45(1):342–355.
作者简介:王旸(1985.09—),男,汉族,江苏镇江人,中级工程师,硕士,研究方向:大数据应用、数据安全。