基于集成学习的二次协同数据预测及优化方法

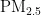
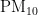
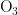
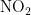
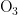
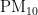
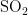
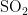
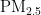
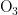
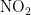
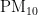
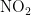
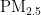
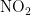
关键词：Fancyimpute库；数据插补；集成学习；BaggingRegressor模型；二次模型；协同预测模型中图分类号：TP391.4 文献标识码：A 文章编号：2096-4706（2025）07-0029-12

Abstract：The commonly used air quality prediction model has poor prediction efect on unknown conditions，and theactualmeteorologicalconditions haveasignificant impactontheconcentrationofairpollutants.Inorder toreduce the errorcausedbymeteorologicalconditionstothe model predictionof polutionconcentration，itisofgreat significance to obtain amodel with good prediction acuracy.Therefore，this paper proposes aquadraticcollaborative data prediction and optimization method basedon Ensemble Learning.Firstly，it combines the measured data with primary predicted data，and usestheFancyimpute libraryfordata interpolation for misingand deviating from the normal distribution data.Secondly，the BaggingRegressr model inEnsemble Learning is used toconstruct aquadratic model，adtheinfluence of meteorological conditions onpollutantconcentration isanalyzed fromthewhole tothe individual.Thevoting mechanism is usedtosynthesize allthe pedictionresults，andtheensemblepredictionresultsareobtained.Finally，acollborativedatapredictionmodelis constructed，andtelocationrelationshipndinddirectionfactorsareicludedforomprehensiveprediction.Theexprimetal results showthat themethodcanefectivelyimprovethepredictionaccuracyofthedataandthecolaborativepredictionmodel improves the prediction accuracy of the monitoring points.

Keywords：Fancyimpute library;data interpolation;Ensemble Learning; BaggingRegresor model;quadratic model; collaborative prediction model

0 引言

绿色环保理念日益深入人心，人类社会建设始终秉持可持续发展观念。然而，随着城市化与工业化建设进程的加快，环境空气质量受到极大冲击，日益恶化的空气已危害到人们的生活质量和生命健康[]。因此，秉持可持续发展观念，重视空气保护及污染治理

问题至关重要[2]。

空气质量指数是反映空气质量的重要指标[3]。大气污染物产生于人类活动或自然过程中，是对环境和人类具有有害影响的物质排入大气的结果。当大气污染物浓度超过环境所能允许的极限范围，空气的正常组成就会遭到破坏。这不仅破坏自然的物理、化学和生态平衡体系，还对人类健康和生态系统造成严重影响。所以，为减少大气污染危害，空气治理势在必行[46]。提高空气质量的关键在于建立空气质量预测模型，该模型能够更准确地预测未来空气质量状况，以便采取相应的控制举措[7]。

《中国统计年鉴》相关数据显示，我国空气污染物主要有二氧化硫、二氧化氮、粒径小于 1 0 μ m 的颗粒物、粒径小于 2 . 5 μm 的颗粒物、臭氧、一氧化碳这六种监测指标[8]，其化学表达式分别为 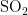、 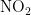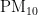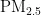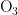， ， ， 、CO。臭氧是氧气经紫外线照射后发生光化学反应的产物，是六项污染物中唯一的二次污染物，这加大了预测臭氧浓度变化精确度方面的难度[9-14]。空气质量影响因素复杂，在建立二次模型时，采用实测数据和一次预测数据相结合的方式，能更全面地综合各影响因素的诸多特征，对提高模型预测的准确度具有重要意义。

后续章节安排如下：第1章主要归纳空气质量预测模型的原理，介绍经再建模及优化后的二次模型在空气质量预测方面的流程；第2章介绍基于集成学习的二次协同数据预测及优化方法，涵盖二次模型和协同模型的数据预测及优化内容，具体阐述空气质量分指数与首要污染物的概念、二次模型数据插补方法和气象条件分类方法、协同模型预测方法，通过综合各项预测得出最终的集成预测结果；第3章为实验与结果分析，为更直观地展现污染物浓度预测值和真实观测值之间的差异，对模型求解结果采用不同监测点数据进行对比验证；最后，对模型予以总结。

1空气质量预测二次模型

大气中的二次污染物，经过一系列化学反应和光化学反应后，生成的新污染物对环境和人体的危害通常比一次污染物更为严重，这致使一次模型在预测污染物浓度变化时，精确度降低，因此需进行二次建模[15-16]。二次预测模型将实测数据与一次预测数据相结合，以此提高预测的准确度。二次模型优化的WRF-CMAQ空气质量预测流程如图1所示，利用污染排放清单以及气象场、地形数据，通过运行WRF-CMAQ模型生成一次预报数据。实测数据是空气质量监测站点实际检测得到的数据，通常一次预报数据和实测数据相关性较低。为使预测数据更具全面性，将一次预报数据与实测数据相结合进行修正，从而让进入二次模型的数据能够捕获更多实际信息。

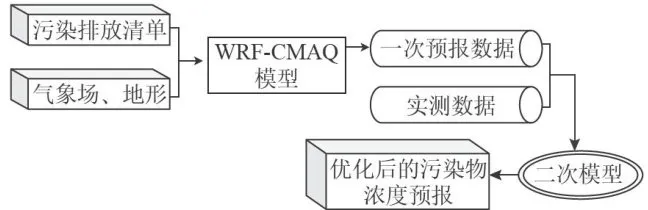图1二次模型优化的WRF-CMAQ空气质量预测过程

空气质量预测是基于气象条件和污染源排放情况，其数据通过耦合物理、化学机制的空气质量模型进行预测的过程。目前，常用的空气质量预测模型是WRF-CMAQ模型，该模型主要由WRF和CMAQ两部分组成[17]：第一部分WRF是一种中尺度数值天气预报系统，为模型提供数据支持；第二部分CMAQ充分考虑了“一个大气”理论，利用WRF提供的气象及污染源排放数据，通过物理和化学反应模拟污染物的变化过程，将复杂的污染情况视为一个整体进行综合处理，进而得出具体时间点或时间段的预测结果，是一种大气环境数值模拟工具。

WRF-CMAQ模型结构[18如图2所示。WRF结构融合静态地形和网络化初始气象场两方面数据，经数据预处理，将数据转化为该结构可处理的形式，随后针对云微物理、积云对流、长波辐射、短波辐射、近地面层、边界层以及路面过程开展参数化物理过程，以此模拟气象情况，生成气象信息。将此气象信息输入到MCIP接口模块[19]，与排放清单、ICON初始化模块、BCON边界值模块和JPROC光化学分解率模块的信息相结合，再把结合后的信息输入到CCTM化学传输模块，进而实现对污染浓度的模拟。

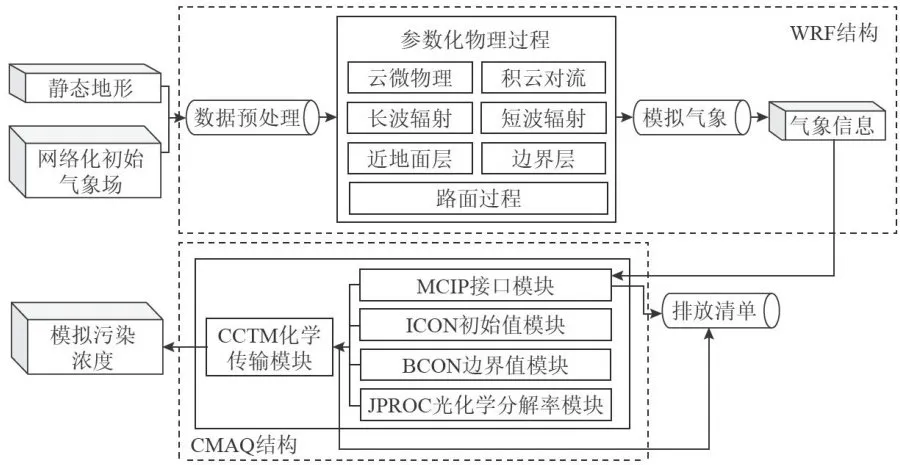图2 WRF-CMAQ模型

WRF-CMAQ模型受模拟气象场以及排放清单不确定性的限制，使得一次预报数据和实测数据相关性较低。二次模型为使预测数据更具有全面性，将一次预报数据结合实测数据进行修正，使得进入二次模型的数据能更多地捕获实际信息。

2空气质量分指数与首要污染物

空气质量指数（AQI）是污染物空气质量分指数（IAQI）的最大值[3，20-21]，是判别空气质量等级的重要指标，分指数数值最大的污染物即为首要污染物[22]。全球各国环境空气质量标准指出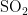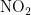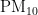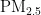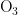， 、 ， ， ， 和CO是主要的污染物项目[23]。通过数据集中“监测点A逐日污染物浓度实测数据”，找出六项污染物的质量浓度值，依据空气质量分指数和污染物项目浓度限值，分别找出各污染物浓度限值最接近的高低位值，进而确定对应的空气质量分指数，计算每天各污染物的IAQI值，进位取整后选取分指数数值最大的作为空气质量指数，并将其对应的污染物确定为首要污染物。空气质量分指数（IAQI）及对应的污染物项目浓度限值如表1所示。

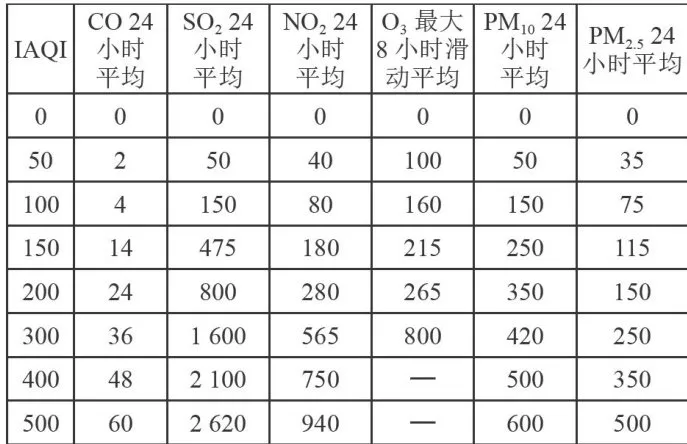表1IAQI及对应的污染物项目浓度限值

3 二次协同数据预测及优化方法

基于集成学习的二次协同数据预测及优化方法如图3所示。在该流程中，运用Fancyimpute库对实测数据与一次预测数据实施数据插补操作，随后借助BaggingRegressor模型构建二次模型以及协同数据预测模型。

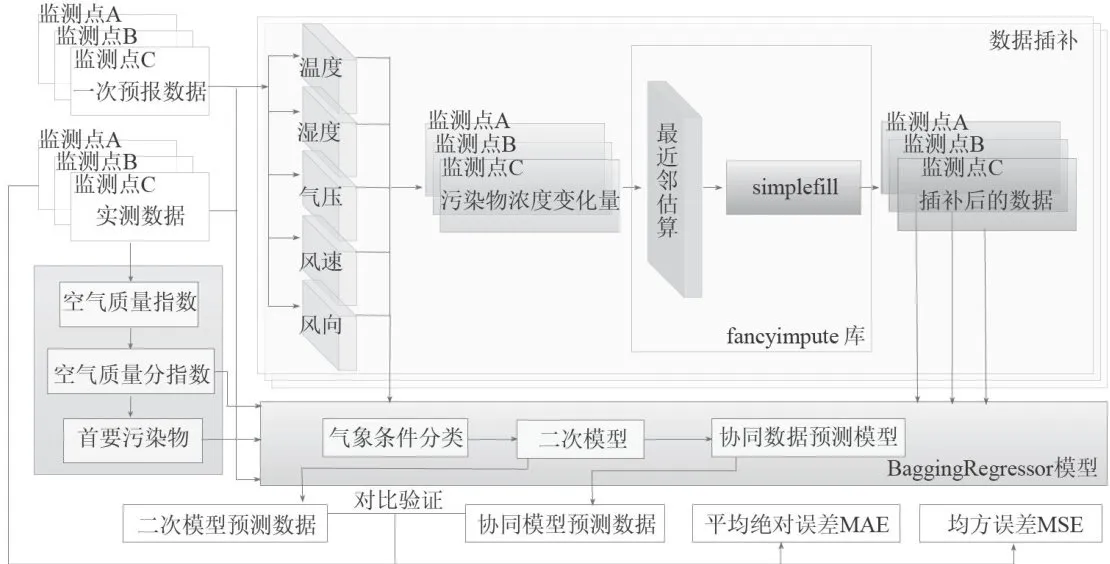图3基于集成学习的二次协同数据预测及优化方法

3.1 符号说明

本文所涉及符号说明如表2所示。

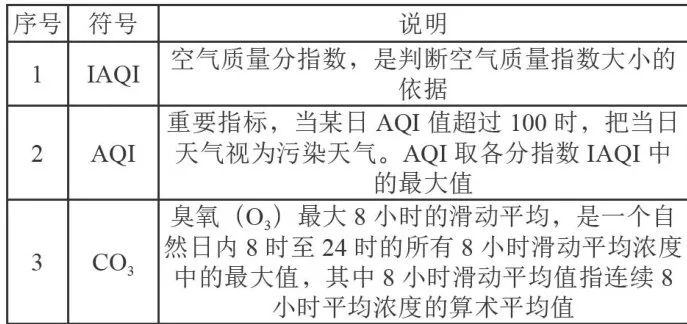表2符号说明（续表）

3.2二次模型数据预测及优化

受服务器断电、设备调试维护等情况影响，一次预报数据存在异常值和缺失值，且模型数据集数据体量庞大，这对数据分析及预测的准确性构成极大考验。因此，本文采用将实测数据与一次预测数据相结合的方法，把空气质量分指数与首要污染物信息合并，利用Fancyimpute库进行数据插补，生成预处理后的数据。接着，将预处理后的数据集成到BaggingRegressor类器中，得到气象条件分类结果。最后，对所有预测结果进行综合，得出最终的集成预测结果。

3.2.1 数据插补

本文对异常数据开展预处理，运用Fancyimpute包中的最邻近节点算法（KNN）、SimpleFill方法对缺失值和异常值实施数据插补，进而计算得出各个污染物的AQI。其中，SimpleFill利用每列的平均值或者中位数填充缺失值；KNN最近邻估算则通过采用两行均具有观测数据特征的均方差对样本进行加权，随后运用加权结果进行特征值填充。当污染物排放情况保持不变，且地区的气象条件有利于污染物扩散或沉降时，该地区的空气质量指数会发生变化。

3.2.2 气象条件分类

BaggingRegressor是一种基于集成学习的回归器，通过投票或平均的方式聚合每个弱学习器的预测结果，从而获得更准确的整体预测。在BaggingRegressor构建过程中引入随机化并对其进行集成，这一操作通常可作为减少黑盒估计器方差的方法。Bagging是一种集成学习技术，其目的是通过组合多个预测结果来得到更准确的整体预测。

本文建立一个同时适用于数据集中A、B、C三个监测点的二次模型，该模型用于预测未来三天6种常规污染物的单日浓度值，以使二次模型预测结果的AQI预报值最大相对误差尽可能小，首要污染物预测准确度尽可能高。对数据再次处理时，分别选取数据集中A、B、C三个监测点各自需预测的前三天气象一次预报数据、污染物浓度与气象实测数据，以及污染物浓度实测数据作为基础数据。在测试阶段，BaggingRegressor把每个待分类的预报数据依次输入到每个训练好的弱学习器中进行预测，将处理好的数据作为模型的输入数据。最后，借助投票机制对所有弱学习器的预测结果进行综合，得出最终的集成预测结果。

通过观察数据集中“监测点A逐小时污染物浓度与气象一次预报数据”的数据规律，发现预报数据呈现出明显的周期性，然而“监测点A逐小时污染物浓度与气象实测数据”中的实测数据，其周期性不如预报数据显著。实测数据的时间范围为2019年4月16日00：00至2021年7月13日07：00，模型运行日期范围为2020年7月23日至2021年7月13日。实测数据中最新的数据时间为2021年7月13日7：00，一次预报中最新的数据时间为2021年7月15日23：00。鉴于此，以一天的时间间隔作为一个周期，选取每天7：00的数据进行分析。

AQI的数值大小受首要污染物影响，首要污染物可能包含 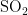、 、 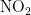、 、 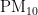、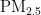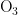CO六种。根据气象条件（温度、湿度、气压、风向、风速）的变化，可得出其对污染物浓度的影响程度，以及气象条件的变化量对每种污染物的影响程度。

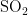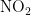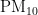
首先，转换“测点A逐小时污染物浓度与气象实测数据”中实测数据的时间格式，提取每天小时数为7的实测数据，计算出一个周期内相同时刻实测数据的气象变化量。将提取的数据按照监测气象条件（温度、湿度、气压、风向、风速的变化）进行归一化处理，使数据处于同一数量级，增强数据指标之间的可比性。其次，在污染物排放情况不变的前提下，AQI的变化反映了对污染物浓度的影响程度。将AQI纳入对气象条件的分类任务中，通过AQI数值的变化，揭示气象条件与首要污染物之间的相关性。具体而言，当地区的气象条件有利于污染物扩散时，污染物浓度会下降，使得该地区的AQI降低；当地区的气象条件有利于污染物沉降时，污染物浓度会下降，进而该地区的AQI下降。最后，构建气象条件与AQI、污染物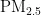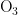（ 、 、 ， 、CO）浓度变化量的相关性矩阵。在AQI或者某一污染物的特定情况下，对气象变化量进行相关性运算。若点积值大于零或者变化量相等，则认定AQI或者某一污染物与这一气象条件相关，并生成可视化结果。

气象条件与AQI及污染物的相关性如图4所示。该图展示了AQI或者某一污染物对各个气象条件的影响程度的可视化结果。横轴表示AQI以及各个污染物 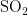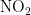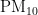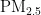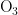（ 、 、 、 、 、CO），左纵轴表示气象条件（温度、湿度、气压、风向、风速），右小长图是左大图的图例。其中，上半部分 0 . 0 0-1 . 0 0 区间内，数值越大颜色越深，表明气象条件对AQI和各个污染物浓度的影响是促进污染物扩散，进而提高污染物的浓度；下半部分 区间内，绝对值越大颜色越深，表明气象条件对AQI和各个污染物浓度的影响是抑制污染物扩散，进而降低污染物的浓度。

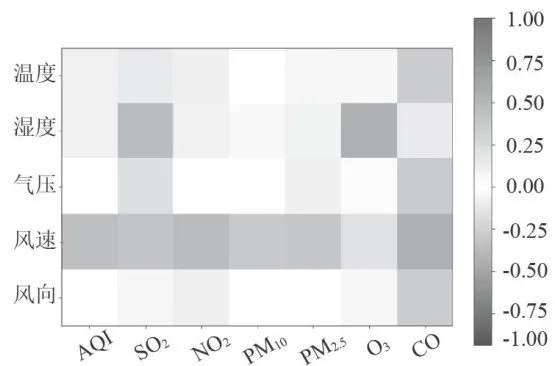图4基于集成学习的二次协同数据预测及优化方法

在污染物排放量不变的条件下，若AQI发生变化，便反映出气象条件对污染物浓度的影响程度。这里所涉及的污染物，可能是首要污染物，也可能是除首要污染物之外的其他污染物。因此，基于气象条件对污染物浓度的影响程度，在对气象条件进行分类时，需从整体到个体逐一开展分析。

各气象条件与污染物浓度变化量关系图如图5所示。其中，横轴表示选取的时间点数，纵轴表示污染物浓度的变化量，深色点代表预测数据，浅色点代表真实数据，能使两种颜色明显区分开的归为一类。从图中可知，气象条件可分为两类：深色点和浅色点能明显分开的温度和气压属于一类，而湿度、风速和风向则归为另一类。再看图4气象条件与AQI及污染物的相关性，由图可见，温度和气压能够较为均匀、直观地被分为两类。所以，从整体上看，温度和气压可归为一类，湿度、风速、风向归为另一类。

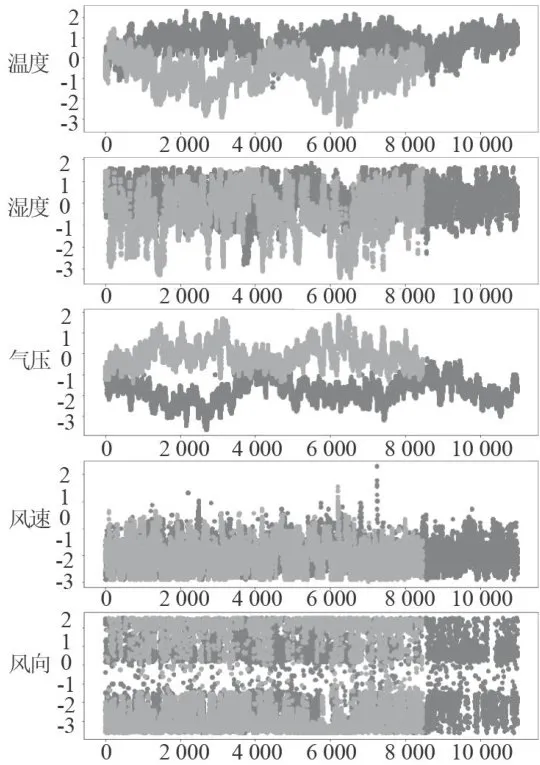图5各气象条件与污染物浓度变化量关系图

观察图4可知，湿度对空气质量指数AQI的影响程度最大，且呈正相关；其他四项（温度、气压、风速、风向）对空气质量指数AQI的影响程度为负数，呈负相关。基于正负相关性，可将对AQI的影响程度划分为两类：湿度为一类，温度、气压、风速和风向归为另一类。AQI数值的变化受首要污染物浓度的影响，而首要污染物可能是 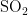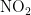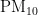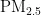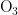， 、 ， 、 、CO这六种中的一种。结合图4对首要污染物逐一分析，不同首要污染物下气象条件的分类情况如图6所示。

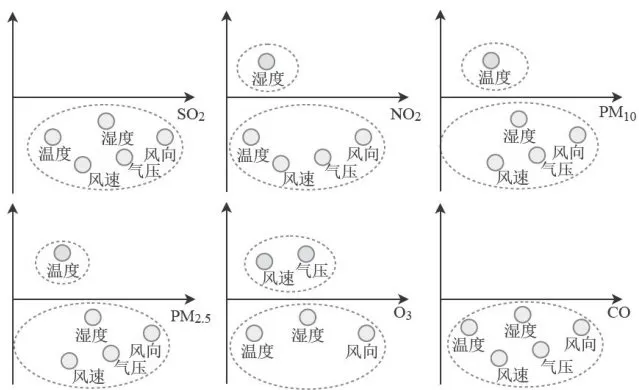图6不同首要污染物下气象条件的分类情况

1）当首要污染物为 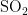时，五种气象条件对 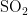浓度的影响程度较大且均呈负相关，基于对 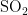浓度的影响程度，可将这五种气象条件归为一类。

2）当首要污染物为 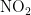时，湿度对 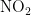浓度的影响程度较大且呈正相关，另外四种气象条件对 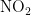浓度均呈负相关，依据对 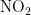浓度的影响程度，可将五种气象条件分为湿度一类，温度、气压、风速、风向一类。

3）当首要污染物为 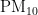时，温度对 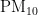浓度的影响程度较大且呈正相关，另外四种气象条件对 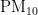浓度均呈负相关，根据对 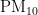浓度的影响程度，可将五种气象条件分为温度一类，湿度、气压、风速、风向一类。

4）当首要污染物为 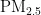时，温度对 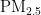浓度的影响程度较大且呈正相关，另外四种气象条件对 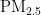浓度均呈负相关，依据对 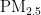浓度的影响程度，可将五种气象条件分为温度一类，湿度、气压、风速、风向一类。

5）当首要污染物为 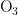时，气压和风速对 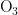浓度均呈正相关，另外三种气象条件对 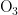浓度均呈负相关，基于对 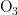浓度的影响程度，可将五种气象条件分为气压和风速一类，温度、湿度、风向一类。

6）当首要污染物为CO时，五种气象条件对CO浓度均呈负相关，根据对CO浓度的影响程度，可将

五种气象条件归为一类。

此外，臭氧属于二次污染物，NO持续转化为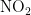 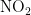， 光解促使 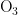逐渐积累并生成。在五种气象条件中，湿度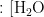（ ）与NO反应会生成 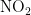，所以湿度加速了二氧化氮的形成。

3.3协同模型数据预测及优化

相邻区域污染物浓度存在一定相关性，区域协同预报或许能够提升空气质量预测的准确度。利用“监测点A空气质量预测基础数据”以及“监测点A1、A2、A3空气质量预测基础数据”，构建包含A、A1、A2、A3四个监测点的协同数据预测模型。

协同数据预测模型采用BaggingRegressor模型。在模型预测过程中，充分考量不同监测点之间的相对位置关系与风向因素，将滑动平均风向作为观测点A1、A2、A3每日平均风向，把每日平均风向与观测点A1、A2、A3和观测点A之间的夹角，作为风向影响力参数，以此提高针对监测点A的污染物浓度预测准确度。

4实验与结果分析

本章节将实验数据及结果绘制成图。为更直观地展现污染物浓度预测值与真实观测值之间的差异，把监测点六种污染物浓度的预测值和真实观测值对比折线图的纵轴，设置为不同的取值范围。

4.1 数据集

本文采用中国研究生数学建模竞赛的数据集，该数据集提供了长期预报基础数据，涵盖污染物浓度、气象一次预报数据以及污染物浓度、气象实测数据。所有一次预报数据的时间跨度为2020年7月23日至2021年7月13日，所有实测数据的时间跨度为2019年4月16日至2021年7月13日，数据总量达十万量级。该数据集每日预报时间为早上7点，预报数据范围包含当日7时前的实测数据，以及运行日期在当日及之前日期的一次预报数据 （预报时间范围截至第三日23时）。而监测时间在当日7时后的逐小时实测数据，以及运行日期在次日及以后的一次预报数据无法获取。

4.2 评价指标

本实验借助平均绝对误差、均方误差这两种评价指标，来判断模型预测及优化后的效果。

平均绝对误差（MeanAbsoluteError，MAE）用于衡量预测值与实际值之间的平均绝对差距，该差值越小，表明模型质量越优，预测准确度越高。其计算式为：

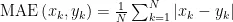
均方误差（Mean Square Error，MSE），是误差平方和的平均值，其计算式为：

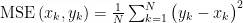
其中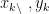， 分别为预测值的第 k 个数据和真实值的第 k 个数据， N 为数据的个数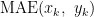， 为平均绝对误差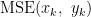， 为均方误差。

4.3二次模型数据预测及优化

4.3.1 监测点常规污染物AQI和首要污染物

通过该二次模型预测监测点A、B、C在2021年7月13日至7月15日6种常规污染物的单日浓度值，并计算出相应的AQI和首要污染物，结果分别如表3至表5所示。从表的最后一列可以看出，基于二次模型，三个预测监测点的首要污染物均为 。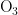

表3监测点A的日值预测结果表4监测点B的日值预测结果表5监测点C的日值预测结果

4.3.2 监测点A的数据对比

监测点A的数据对比折线图如图7、图8所示。其中，图7为监测点A六种污染物浓度的预测值与真实观测值对比折线图，图中从上至下分为6个子图，每个子图对应一种污染物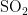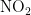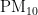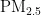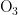（ 、 、 、 、 、CO）的浓度折线，深色折线代表污染物浓度的预测值，浅色折线代表污染物浓度的真实观测值，横轴表示天数，纵轴表示污染物的浓度值；图8是监测点A的AQI真实值与AQI预测值的对比折线图，深色折线表示AQI真实值，浅色折线表示AQI预测值，横轴表示天数，纵轴表示污染物的浓度值。

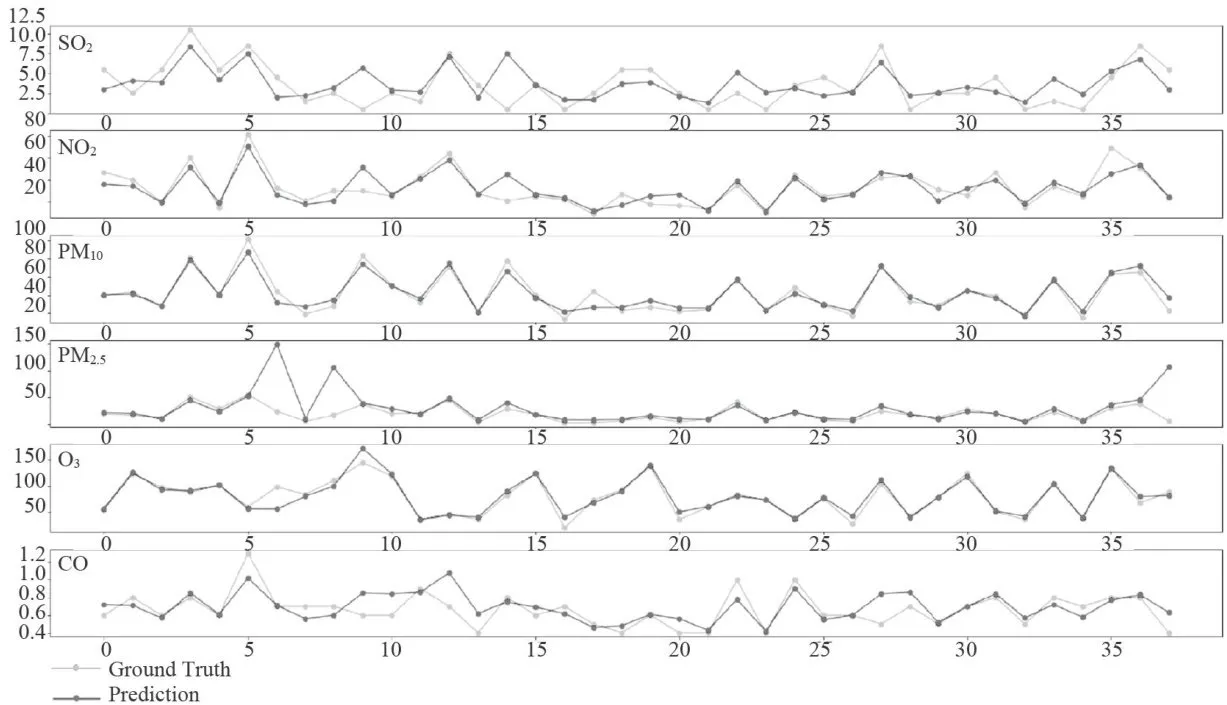图7监测点A的预测值和真实值对比图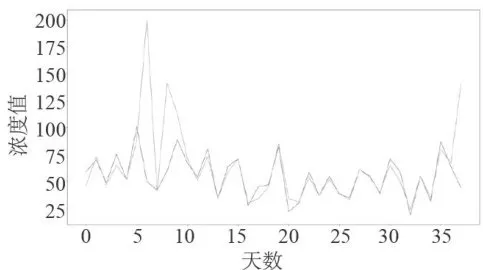图8监测点A的AQI真实值和预测值的对比图

从图7和图8可以看出，经BaggingRegressor模型预测得到的污染物浓度值曲线以及AQI值曲线，与真实观测到的污染物浓度值曲线、AQI值曲线十分接近。此外，经计算，CO污染物浓度的实测数据与预测数据之间的平均绝对误差仅为0.11，均方误差仅为0.01。

4.3.3 监测点B的数据对比

监测点B的数据对比折线图如图9、图10所示。其中，图9是监测点B六种污染物浓度的预测值和真实观测值对比折线图，图中从上到下分为6个子图，每个子图对应一种污染物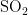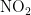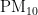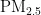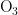（ 、 、 、 、 、CO）的浓度折线，深色折线表示污染物浓度的预测值，浅色折线表示污染物浓度的真实观测值，横轴表示天数，纵轴表示污染物的浓度值；图10是监测点B的AQI真实值和AQI预测值的对比折线图，深色折线表示AQI真实值，浅色折线表示AQI预测值，横轴表示天数，纵轴表示污染物的浓度值。

从图9和图10能够看出，经BaggingRegressor模型预测的污染物浓度值曲线以及AQI值曲线，与真实观测到的污染物浓度值曲线、AQI值曲线极为接近。而且经计算，CO污染物浓度的实测数据与预测数据之间，平均绝对误差仅为0.08，均方误差仅为0.01。

4.3.4 监测点C的数据对比

监测点C的数据对比折线图如图11、图12所示。其中，图11是监测点C六种污染物浓度的预测值和真实观测值对比折线图，图中从上到下分为6个子图，每个子图对应一种污染物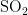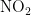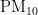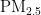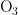（ ， ， 、 、 、CO）的浓度折线，深色折线表示污染物浓度的预测值，浅色折线表示污染物浓度的真实观测值，横轴表示天数，纵轴表示污染物的浓度值；

图12是监测点C的AQI真实值和AQI预测值的对比折线图，深色折线表示AQI真实值，浅色折线表示AQI预测值，横轴表示天数，纵轴表示污染物的浓度值。

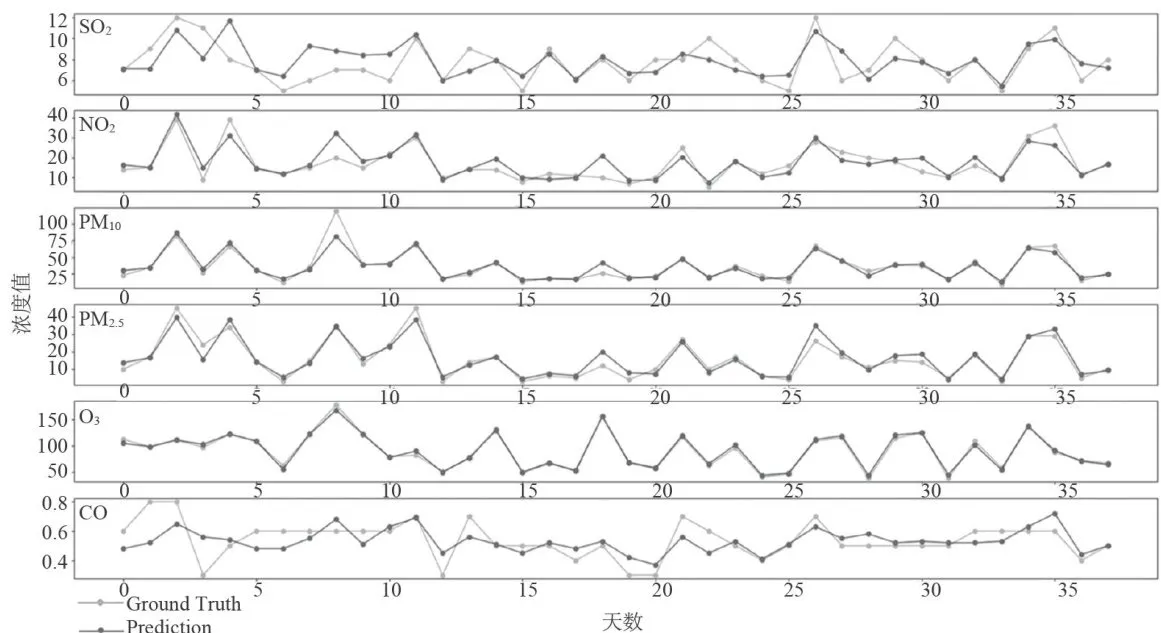图9监测点B的预测值和真实值对比图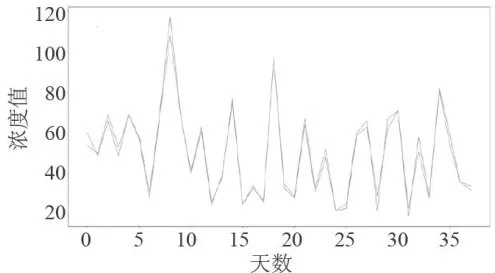图10监测点B的AQI真实值和预测值的对比图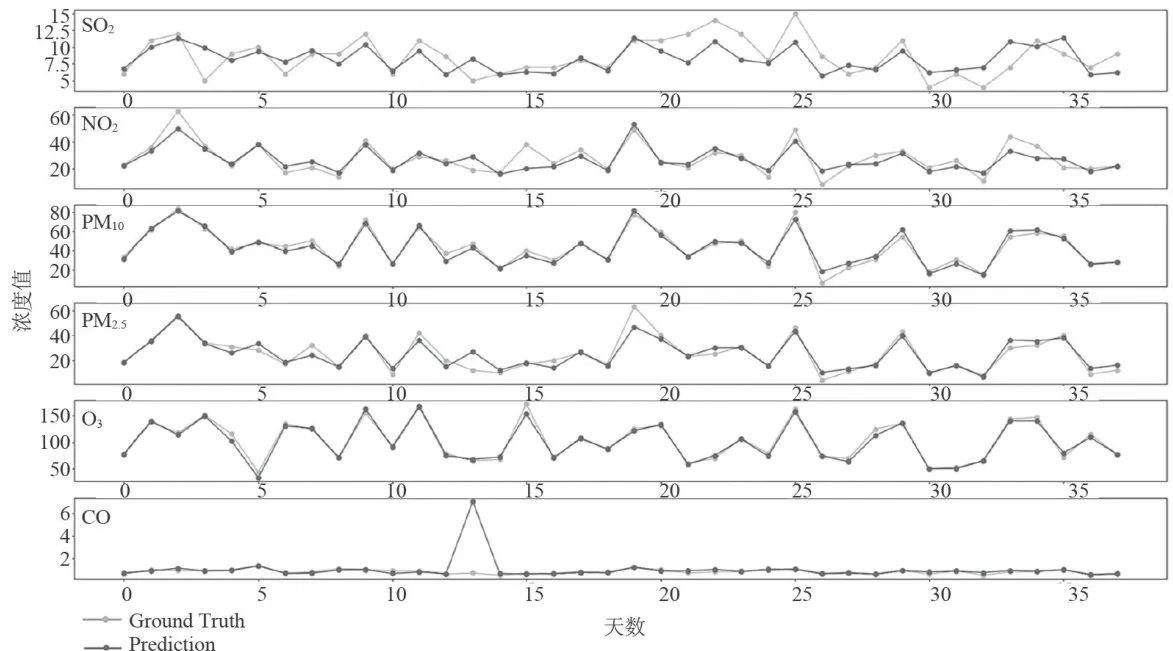图11监测点C的预测值和真实值对比图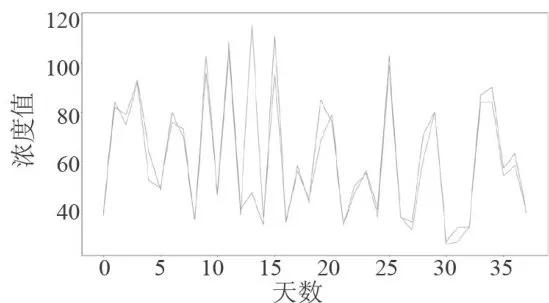图12监测点C的AQI真实值和预测值的对比图

从图11和图12可以看出，经BaggingRegressor模型预测的污染物浓度值曲线以及AQI值曲线，与真实观测到的污染物浓度值曲线、AQI值曲线十分接近。此外，经计算，CO污染物浓度的实测数据与预测数据之间，平均绝对误差仅为0.26，均方误差仅为0.07。

4.4协同模型数据预测及优化

4.4.1监测点常规污染物AQI和首要污染物

通过该协同预测模型预测监测点A、A1、A2、A3在2021年7月13日至7月15日6种常规污染物的单日浓度值，并计算出相应的AQI和首要污染物，结果分别如表6至表9所示。从表的最后一列可以看出，基于协同模型，这4个预测监测点的首要污染物均为 。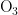

表6监测点A的日值预测结果表7监测点A1的日值预测结果表8监测点A2的日值预测结果表9监测点A3的日值预测结果

4.4.2 监测点A1的数据对比

从图13和图14可以看出监测点A1六种污染物浓度的预测值与真实观测值对比折线图的情况。经BaggingRegressor模型进行3天协同预测得到的污染物浓度值曲线以及AQI值曲线，与真实观测到的污染物浓度值曲线、AQI值曲线极为接近。相较于二次模型数据预测的曲线，其拟合程度更高。这表明考虑了监测点相对位置和风向夹角的协同预测模型，预测误差更小，模型稳定性更佳。此外，经计算，CO污染物浓度的实测数据与预测数据之间，平均绝对误差仅为0.07，均方误差仅为0.01。

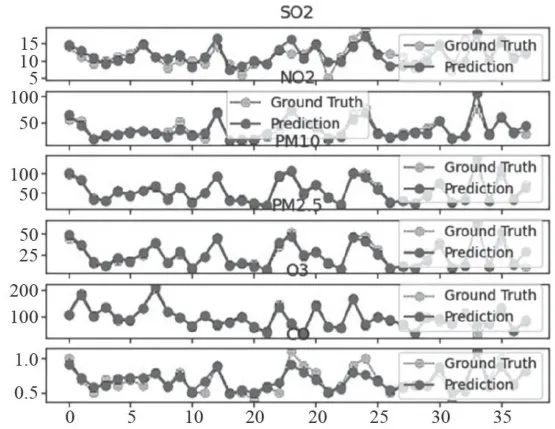图13监测点A1的预测值和真实值对比图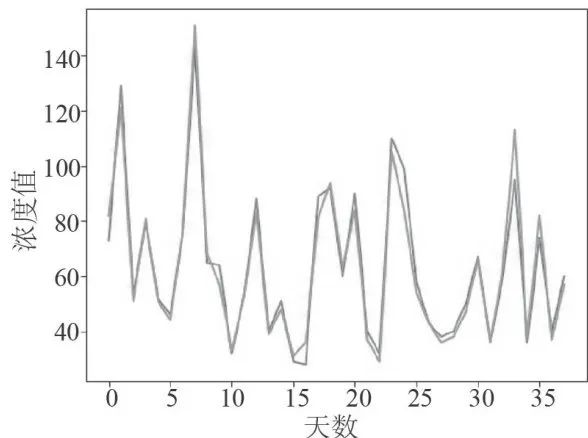图14监测点A1的AQI真实值和预测值的对比图

从图15和图16可以看出监测点A2六种污染物浓度的预测值与真实观测值对比折线图的情况。经计算，CO污染物浓度的实测数据与预测数据之间，平均绝对误差仅为0.08，均方误差仅为0.01。

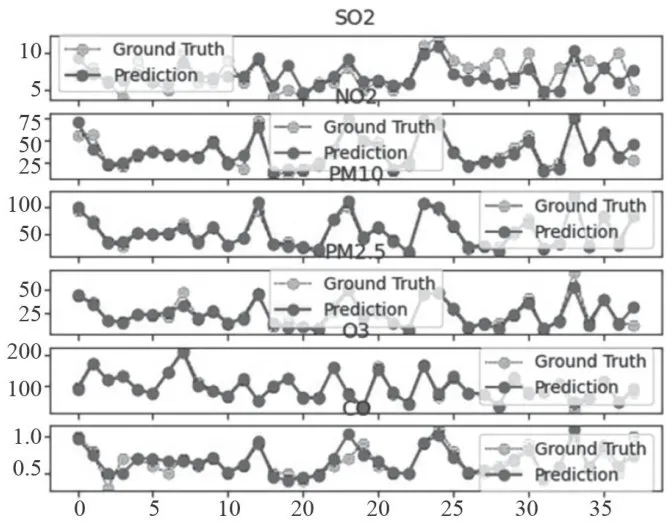图15监测点A2的预测值和真实值对比图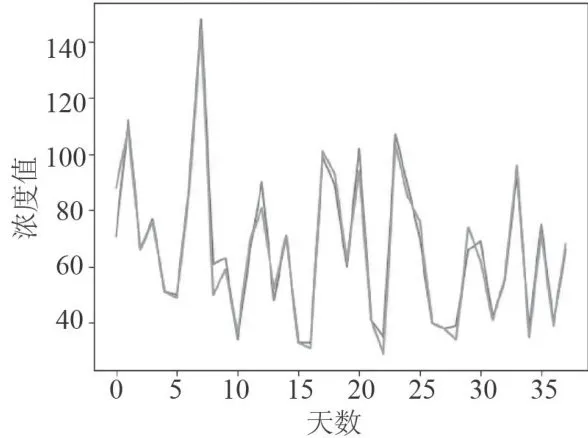图16监测点A2的AQI真实值和AQI预测值的对比图

从图17和图18可以看出监测点A3六种污染物浓度的预测值与真实观测值对比折线图的情况。经计算，CO污染物浓度的实测数据与预测数据之间，平均绝对误差（MAE）仅为0.10，均方误差（MSE）仅为0.01。

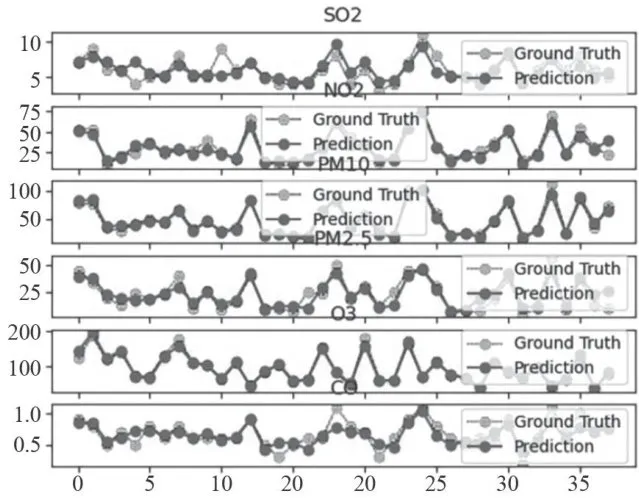图17监测点A3的预测值和真实值对比图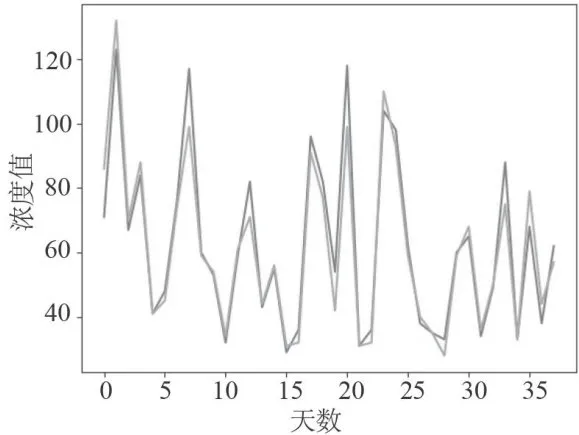图18监测点A3的AQI真实值和AQI预测值的对比图

从图19和图20可以看出监测点A六种污染物浓度的预测值与真实观测值对比折线图的情况。经计算，CO污染物浓度的实测数据与预测数据之间，平均绝对误差仅为0.10，均方误差仅为0.01。

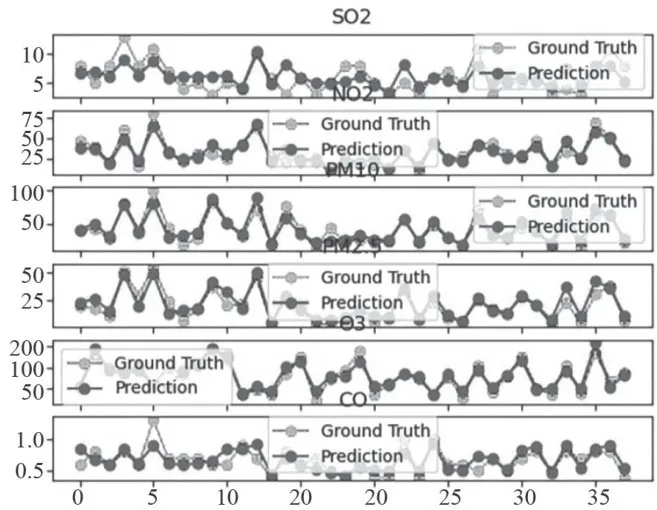图19监测点A的预测值和真实值对比图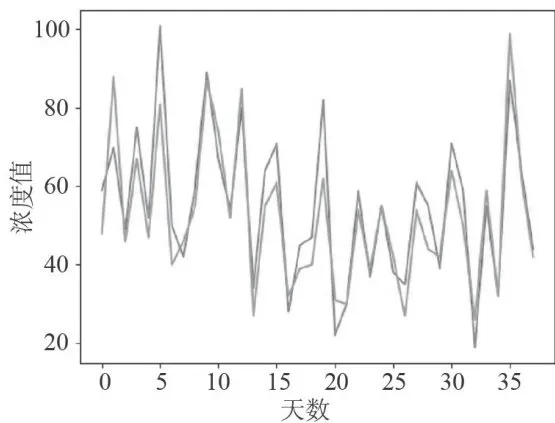图20监测点A的AQI真实值和预测值的对比图

4.5模型精度

与二次预报模型相比，协同预报模型的预训练过程包含了二次模型，且协同模型着重考虑了风向和监测点之间相对关系的影响。协同模型的预测精度如表10所示：监测点A精度为0.78，监测点A1精度为0.84，监测点A2精度为0.87，监测点A3精度为0.89。可见，监测点A的精度低于监测点A1、A2、A3的精度，这进一步明确地显示出协同模型预测误差有所降低。

表10协同模型预测精度

5结论

本文构建了基于集成学习的二次协同数据预测及优化方法，对数据集中多个监测点的基础数据展开挖掘与分析，以此提升空气质量预测的准确性。为确保整体数据的全面性，将实测数据与一次预测数据相结合，针对缺失及偏离正常分布的数据进行数据插补。鉴于实际气象条件对空气污染物浓度影响显著，且气象条件模拟的误差会致使预测污染浓度产生误差，故而利用BaggingRegressor模型构建二次模型与协同数据预测模型。实验结果表明，该方法能够有效提高预报数据的准确性。

参考文献：

[1]杨留明，高帅鹏，黄飞，等.基于神经网络模型对城市空气质量预报方法的优化研究[J].环境监控与预警，2023，15（2）：33-39.

[2]张顺顺，卢彦希，罗崴，等.基于AQI的空气污染物预报研究[J].能源与环境，2024（1）：97-99+120.

[3]俞婧婧，唐立力，吴浩，等.空气质量指数预测方法综述[J].环保科技，2023，29（6）： 5 5 - 5 9 + 6 4

[4]王标，彭瑜，王维，等.数据挖掘在空气质量数值模拟中的应用研究进展[J].环境科学研究，2024，37（8）：1703-1713.

[5]张天娇，海涛，王钧，等.基于LPWAN和AQI指数预测的空气质量监测系统[J].科学技术与工程，2024，24（15）：6558-6566.

[6]李佳成，梁龙跃.基于机器学习方法的空气质量预测与影响因素识别[J].计算机技术与发展，2024，34（1）：164-170.

[7]王梓鉴，罗敏，朱钦权，等.基于多源数据融合的空气质量二次预报模型与计算方法[J].江西科学，2023，41（2）：405-411.

[8]王凯文，李宏滨.基于多元线性回归的空气质量指数预测模型[J].信息记录材料，2024，25（2）：1-3.

[9]朱盛恺，陈劲杰.基于极限学习机模型的空气质量二次预报[J].软件工程，2022，25（8）：39-42.

[10]刘金钠，杨莉军，胡永乐.基于LSTM的空气质量二次预报方法[J].北京印刷学院学报，2023，31（6）：59-63.

[11]MENDEZM，MERAYOMG，NUNEZM.MachineLearning Algorithms to Forecast Air Quality：A Survey [J].ArtificialIntelligenceReview，2023，56（9）：10031-10066.

[12]肖宇.基于多机器学习算法耦合的空气质量数值预报订正方法研究及应用[J].环境科学研究，2022，35（12）：2693-2701.

[13]徐爱兰，朱晏民，孙强，等.基于K-means划分区域的深度学习空气质量预报[J].南通大学学报：自然科学版，2021，20（3）：49-56.

[14]李佳成，梁龙跃.基于机器学习方法的空气质量预测与影响因素识别[J].计算机技术与发展，2024，34（1）：164-170.

[15] LIUQ，CUIBY，LIU Z. Air Quality Class PredictionUsing Machine Learning Methods Based on Monitoring Data andSecondary Modeling[J/OL].Atmosphere，2024，15（5）：553[2024-10-03].https：//doi.org/10.3390/atmos15050553.

[16]李毅军，张振豪，胡健，等.基于BP神经网络的WRF-CMAQ优化方法[J].微型电脑应用，2023，39（7）：161-164.

[17] WANG J，ZHANG W，SHI W，et al.Analysis of theCauses of an O3 Pollution Event in Suqian on 18-21 June 2020Based on the WRF-CMAQModel[J/OL].Atmosphere，2024，15（7）：831[2024-08-21]. https：//doi.org/10.3390/atmos15070831.

[18]伯鑫.空气质量模型（SMOKE、WRF、CMAQ等）操作指南及案例研究[M].北京：中国环境出版集团，2019.

[19]LIJL，YUSC，CHENX，etal.Evaluationofthe WRF-CMAQ Model Performances on Air Quality in Chinawith the Impacts of the Observation Nudging on Meteorology[J/OL].Aerosol and Air Quality Research，2022，22（4）：220023[2024-09-20].https：//doi.0rg/10.4209/aaqr.220023.

[20] MEENA D PK，SINGHD V. Air Quality Monitoringand Pollution Control Technologies [J].International JournalofMultidisciplinary Research in Science，Engineering andTechnology，2024，7（2）：4409-4426.

[21] SACHDEVA S，SINGHH，BHATIA S，et al.AnIntegrated Framework for PredictingAir Quality Index UsingPollutantConcentrationandMeteorologicalData[J].MultimediaTools and Applications，2024，83（16）：46967-46996.

[22]LIUWB，LINGXB，XUEY，etal.Studyon theConcentrationofTopAirPollutantsinXuzhouCityin Winter2020 Based on the WRF-Chem and ADMS-Urban Models [J/OL].Atmosphere，2024，15（1）：129[2024-09-23].https：//doi.org/10.3390/atmos15010129.

[23]和金梅，王宗爽，郭敏，等.全球环境空气质量标准研究及未来我国标准展望[J].环境科学研究，2024，37（9）：1897-1910.

作者简介：梁丽娜（1996一），女，汉族，河北雄安人，研究实习员，硕士，研究方向：机器学习与数据挖掘；张宇（1998一），男，汉族，山东德州人，助教，硕士，研究方向：图像处理；张嘉玮（1993一），男，汉族，河北唐山人，硕士在读，研究方向：机器学习与数据挖掘。