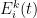
中图分类号:TP391 文献标识码:A 文章编号:2096-4706(2025)07-0133-06
Abstract:Inorder toimprove theaccuracyofpost-earthquake emergencymaterial demandforecasting,this paper proposes afeatureweightllocationmethodbasedonimprovedCase-BasedReasoning(CBR)algorithm,andconstructsapost-earthquake emergencymaterial demand forecasting modelbasedonsafetystock theory.The model isbasedonseven earthquakedisaster indicatorssuchasagntude,focaldepth,artquakeocrecetime,populationdensityumberofousecollaps,eisic fortificationintensityandseismicintensity.Itcanacuratelyforecastthedemandforvarioustypesofemergencymaterialsafter theearthquake.The experimentalresults show thatthe MeanRelative Errorof the forcast valueobtained bythe forecasting model optimized bygame theory-improved geneticalgorithm(SAGA)and Analytic Hierarchy Process (AHP)algorithmare 89 . 5 7 % and 8 7 . 5 1 % lower than that obtained by GA algorithm optimization and SAGA algorithm optimization,respectively. This showsthat the modelcan providestrong technicalsupport for theeffcientallocationofpost-earthquake emergency materials.
Keywords: post-earthquake emergency material; demand forecasting; game theory; SAGA algorithm; Case-Based Reasoning algorithm
0 引言
中国位于欧亚地震带和环太平洋地震带之间,地震灾害的频繁发生严重威胁着国家的社会建设、经济发展和人民生命安全[。虽然我们无法完全避免地震灾害所带来的影响,但通过采取积极有效的措施,可以尽量减少灾害所造成的各种损失[2]。地震灾害具有极强的破坏性,人员伤亡和人口迁移等情况不可避免,为最大程度救助伤员和保障灾民的生存,必须实现应急资源的优化配置,合理利用有限的运输力量,以最快的速度向灾区运送最紧缺的应急物资。要实现最优配置,就必须解决应急物资需求的预测问题[3。在地震灾害发生初期,政府需要利用有限的决策信息做出应急决策。如何在信息不足的情况下实现应急物资需求的精确预测,是政府梯次配置和高效调配的关键问题。
目前,国内外学者针对应急物资需求的精确预测进行了大量研究,主要集中在神经网络预测法和案例推理法两大类。前者的代表主要为BP神经网络算法[4,后者在应急需求预测方面已十分成熟[7-9]。考虑到神经网络算法受限于震后应急物资需求案例少、无法进行大量数据训练的问题,结合应急物资需求量与受灾人口数量直接相关的预测特点,本文采用案例推理法建立震后受灾人口数预测模型。鉴于传统的主观赋权法[10]缺乏客观依据,存在不确定性,因此,本文提出了一种基于博弈论-SAGA-AHP算法的主客观组合赋权的预测方法。该方法首先基于遗传算法(Genetic Algorithm,GA)[1]引入模拟退火算法(Simulated Annealing,SA)[12],形成混合的模拟退火-遗传算法 (Simulated Annealing and Genetic Algorithm,SAGA),对案例推理模型的各属性进行客观权重分配。再通过层次分析法(Analytic HierarchyProcess,AHP)借鉴专家经验知识对模型属性进行主观权重分配,并引入博弈论思想将两种属性权重进行优化融合,提高震后受灾人口数量预测模型的精度。最后,利用安全库存理论,对不同种类应急物资的需求量进行预测。仿真实验表明,与GA、SAGA赋权的预测模型相比,博弈论-SAGA-AHP算法赋权后的模型预测精度更高。
1震后受灾人口数量预测的基本理论
本文将案例推理模型、博弈论、SAGA算法与层次分析法进行了有效融合,以案例推理模型预测结果作为深入融合其他3个算法的基础条件,进而设计出基于博弈论-SAGA-AHP算法改进案例推理法,震后应急物资需求预测建模流程,并通过该流程进行特征权重分配,具体如图1所示。
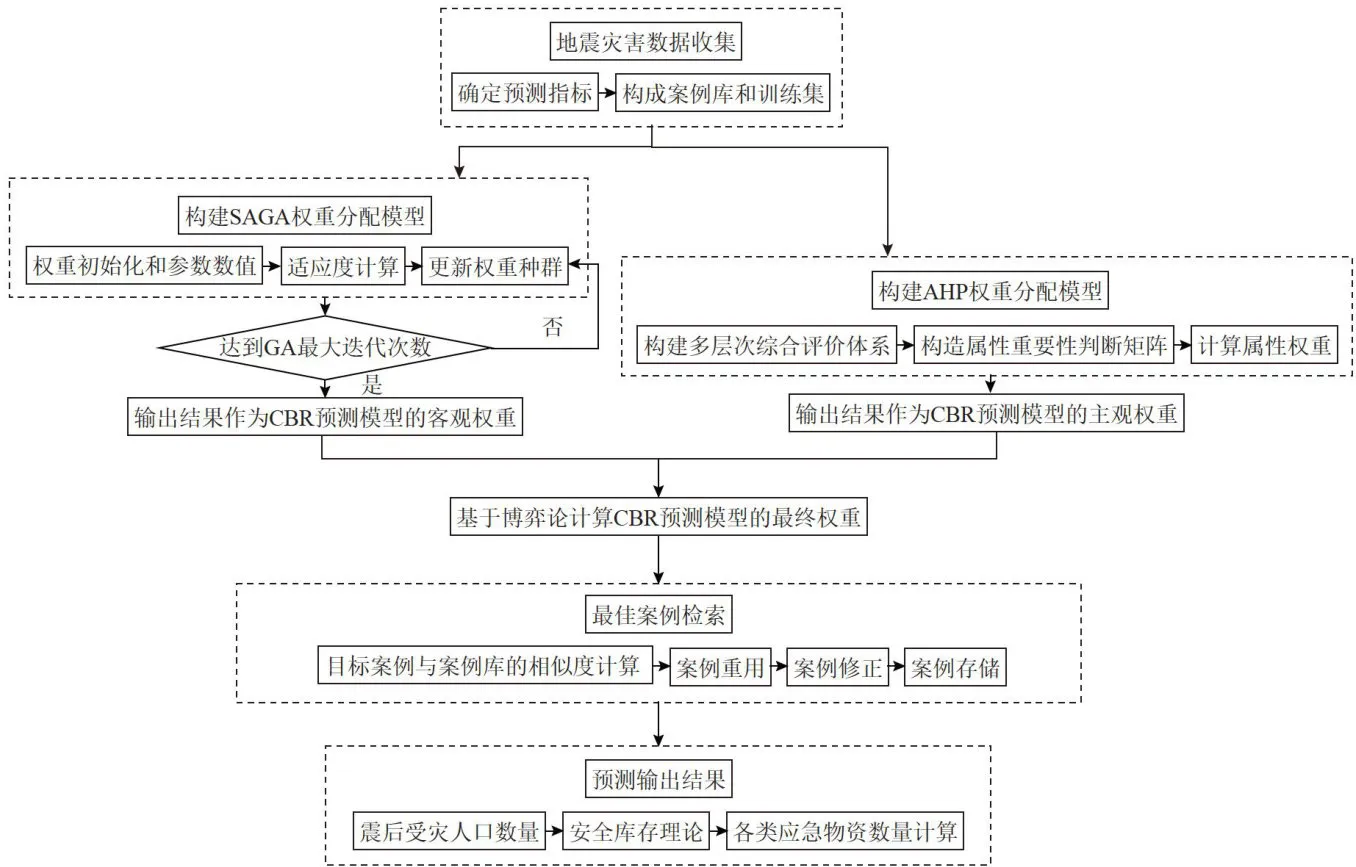 图1震后应急物资需求预测建模流程
图1震后应急物资需求预测建模流程从图1中的建模流程中可以看出,本文进行震后应急物资需求预测的步骤主要包括以下几个方面:首先,收集地震灾害原始数据,确定关键属性作为预测指标,并构建案例库;其次,分别构建基于SAGA算法和AHP的权重分配模型,并利用博弈论得到预测模型的最优权重分配结果;接着,基于CBR对目标案例进行最佳相似案例的检索、重用和修正,从而得到震后受灾人口数量;最后,根据安全库存理论对震后各类应急物资需求量进行计算。
2基于博弈论-SAGA-AHP算法的特征权重分配
2.1 SAGA算法实现
根据SA和GA原理,SAGA算法结构如图2所示。在采用SAGA算法分配权重前,需要初始化N组特征权重种群,其中每组特征权重代表一个个体。通过GA“优胜劣汰”的运算机制,经过选择、交叉、变异操作,保留适应度较强的个体,完成权重的初步优化过程,得到当前迭代的最优权重。如果未达到预设的迭代次数,采用SA算法继续寻找当前最优权重至温度最低,从而实现完整的单次权重寻优。
开始↓初始化权重种群 T 选择适应度高 的个体复制 交换操作 ↓ 否 Prandom √是否 交支批作 插操作 新解新解 否+ 降温操作结束 ↓ 更新种群 √ 新解误差率 是 ?低于旧解 达到SA最大是 否 迭代次数
下面首先介绍适应度函数的定义,然后介绍SA算法的权重寻优,最后介绍采用SA算法进行特征权重的进一步优化,从而得到最优特征权重的近似解,具体内容如下:
1)定义SAGA算法的适应度。本文将CBR预测模型的平均相对误差(MeanRelativeError,MRE)的倒数定义为SAGA算法中权重寻优的适应度函数f ,即:
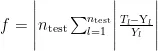
其中, 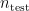 为测试集中案例数量;
为测试集中案例数量; 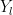 为第 l 个测试案例的实际输出值;
为第 l 个测试案例的实际输出值; 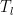 为第 l 个测试案例的预测值。
为第 l 个测试案例的预测值。
2)基于SAGA的权重优化。根据GA算法原理,基于欧式距离式为:
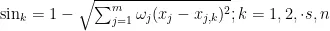
其中, 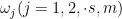 为第 j 个特征属性的权重,所有特征权重需满足:
为第 j 个特征属性的权重,所有特征权重需满足:
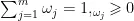
首先,进行相似度计算,并随机生成 N 组初始权重,接着依据式(1)逐一计算 N 组权重中每组权重对应的适应度 f ( Ω ( h ) ) ,然后,执行选择、交叉和变异操作,并采用轮盘赌的方法选取适应度值高的特征变量,得到新的迭代权重。
通过GA算法得到权重种群内当前最佳适应度所对应的权重和当前最佳适应度,分别记为 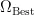 和
和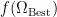 。
。
然后采用SA算法继续寻找当前最佳权重。将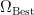 作为SA算法的初始值,在权重
作为SA算法的初始值,在权重 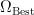 附近进行交换、逆转或插入操作产生新的权重
附近进行交换、逆转或插入操作产生新的权重 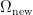 ,并计算其适应度
,并计算其适应度 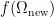 ,再根据Metropolis准则判断是否接受新权重。
,再根据Metropolis准则判断是否接受新权重。
Metropolis准则可表示为:
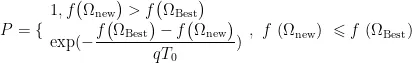
其中, 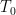 为初始温度, q 为冷却因子。若
为初始温度, q 为冷却因子。若 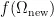
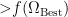 ,则无条件保留
,则无条件保留 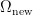 ,否则根据两者的适应度值差值概率公式
,否则根据两者的适应度值差值概率公式 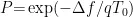 来判断是否选择该个体。
来判断是否选择该个体。
当降温次数达到最大时,表明SAGA算法一次迭代寻优结束。此时,将本次迭代得到的最优权重矩阵 ±bΩ 作为GA算法的初始权重矩阵,进入下一次迭代寻优。重复此过程,直至达到设定的迭代次数,最终得到最优权重矩阵和最优权重的近似解。
2.2 AHP算法实现
以地震危害程度指标、地区抗震指标2个影响受灾人口数量的关键因素进行划分,构建以目标层、准则层和指标层为主体的多层次综合评价体系。具体的层次结构如图3所示。
目标层: 震后受灾人口数量案例库案例匹配A1
准则层:地震危害指标B1 地区抗震指标B2√ ↓ √ 3 1 7
指标层:! 震级 震源深度2 地震烈度3 地震发生时间 设防烈度 人口密度3 房屋倒塌数量7x1x5x4
3 实验研究
为了验证基于博弈论-SAGA-AHP特征权重优化算法的CBR震后受灾人数预测模型的有效性,本文选取了7项特征属性构建震后信息案例库,分别为:f1:震级、f2:震源深度、f3:地震发生时间、f4:人口密度、f5:房屋倒塌数量、f6:设防烈度和f7:地震烈度,用于对受灾人口数量 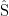 进行准确预测。通过与GA算法和SAGA算法优化特征权重的CBR震后受灾人口数量预测模型进行对比,验证模型的
进行准确预测。通过与GA算法和SAGA算法优化特征权重的CBR震后受灾人口数量预测模型进行对比,验证模型的
有效性。
3.1 数据来源
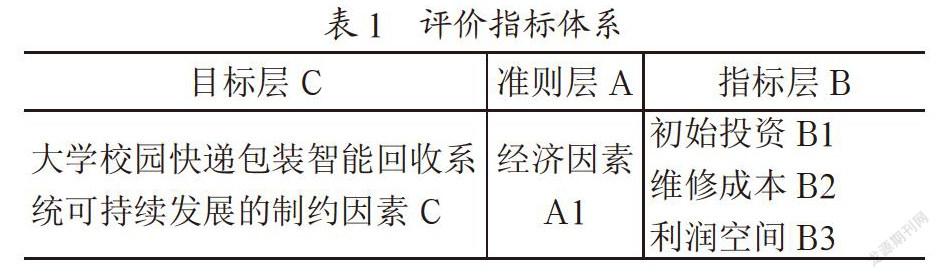
本文数据来源主要包括国家地震科学数据共享中心、地方各级人民政府、学术论文以及新闻报道。通过筛选给出了震级在6级以上的地震灾害数据30例。表1为统计的地震数据部分信息。
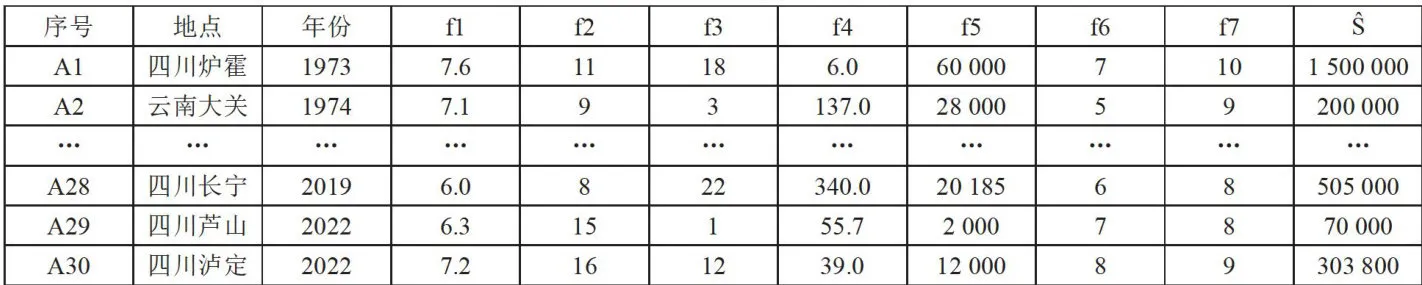 表1地震相关数据部分统计表
表1地震相关数据部分统计表3.2 仿真实验
设定CBR相关参数为:案例 1 ~ 2 5 设为案例库,案例 2 6 ~ 3 0 作为测试集;设定GA相关参数为:初始种群个数为100,遗传迭代次数为600,交叉概率为0.8,变异概率为0.05;设定SA相关参数为:外循环迭代次数为300,内循环迭代次数为50,初始温度为100,冷却因子为0.99,交换操作概率为0.2,逆转操作概率为0.5,插入操作概率为0.3。经MATLAB编程计算,利用GA算法可得到客观权重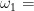 (0.28,0.01,0.03,0.10,0.30,0.04,0.24),利用SAGA算法可得到的客观权重
(0.28,0.01,0.03,0.10,0.30,0.04,0.24),利用SAGA算法可得到的客观权重 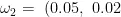 0.01,0.07,0.66,0.18,0.01)。具体优化过程如图4所示。
0.01,0.07,0.66,0.18,0.01)。具体优化过程如图4所示。
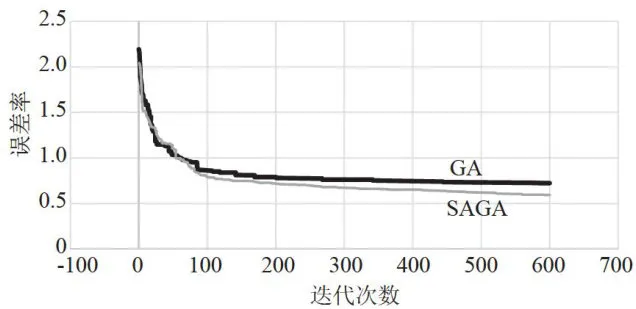 图4优化过程示意图
图4优化过程示意图从图4中可以看出,粗黑线代表GA的优化过程,灰线代表SAGA的优化过程。从曲线的变化趋势来看,灰线相较于粗黑线水平直线的情况更少更短,误差率更低,这表明SA操作起到了跳出局部最优的效果。整体而言,SAGA的表现比GA更加优秀。
基于APH算法计算的主观权重 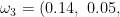 0.02,0.05,0.54,0.11,0.09),利用博弈论建立最优组合系数方程组:
0.02,0.05,0.54,0.11,0.09),利用博弈论建立最优组合系数方程组:
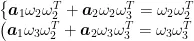
求解得 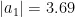 ,
, 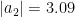 ,归一化处理后得到
,归一化处理后得到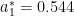 ,
, 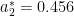 。最终可得综合指标权重 ω = (0.14,0.05,0.02,0.08,0.44,0.19,0.08)。
。最终可得综合指标权重 ω = (0.14,0.05,0.02,0.08,0.44,0.19,0.08)。
为验证模型可行性并对比算法的改进效果,对案例库分别采用GA、SAGA、博弈论-SAGA-AHP算法进行10次仿真实验验证,从预测精度MRE对比算法的优劣,结果如表2所示。
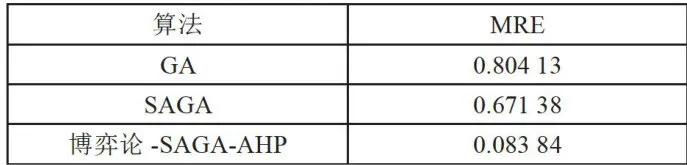 表2模型预测精度对比
表2模型预测精度对比根据表2可知,基于博弈论-SAGA-AHP算法的震后受灾人口数量预测模型在10次实验的平均相对误差MRE的平均值为0.10384,明显低于GA算法和SAGA算法各自对应的统计量的取值。图5为MRE对比图。博弈论-SAGA-AHP算法获取的受灾人口数量预测值的平均相对误差分别比GA和SAGA算法获得的平均相对误差小 8 9 . 5 7 % 和 8 7 . 5 1 % 。
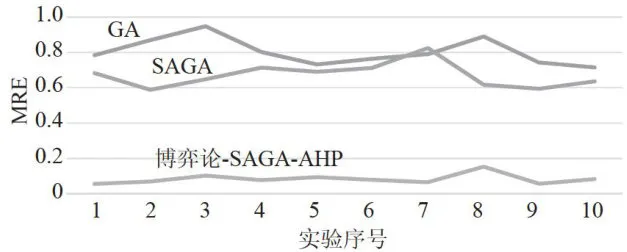 图5MRE对比图
图5MRE对比图从图5中可以看出,博弈论-SAGA-AHP算法在三种算法中不仅波动最小而且总体最稳定。由实验结果得出,博弈论-SAGA-AHP算法显著提高了受灾人口数量的预测精度。
4构建震后应急物资需求预测模型
4.1 预测问题描述
地震灾害发生后,基于灾区受灾人口数量,考虑各类应急物资供应的提前期,准确预测灾区各类应急物资的需求量。本文结合安全库存理论[13],考虑震后初期饮食类、医疗类、御寒类这三类物资直接关系受灾群众基本生存的维持,利用博弈论-SAGA-APH算法预测地震灾害发生后的受灾人口与三类物资之间的关系,建立震后应急物资需求预测模型,间接对地震灾害中的应急物资需求进行预测。
4.2 预测模型构建
设地震灾害发生后,援助灾区的初始时刻为0,以小时为单位计时,记 t ( t = 0 ,1,2,…)。地震灾害应急物资预测模型中使用的数学符号定义如下: k 为某种应急物资,如水、食物、药品等; 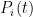 为在时间t 内的受灾人口数量;
为在时间t 内的受灾人口数量; 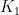 为饮食类用品,包括饮用水、食物等;
为饮食类用品,包括饮用水、食物等; 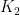 为医疗类用品,包括消炎药、防疫药物等;
为医疗类用品,包括消炎药、防疫药物等;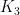 为御寒类用品,包括帐篷、衣服等; ϕ 为应急物资供应的服务水平,即物资供应对灾区人民需求的满足程度;
为御寒类用品,包括帐篷、衣服等; ϕ 为应急物资供应的服务水平,即物资供应对灾区人民需求的满足程度; 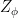 为在服务水平 ϕ 的基础上,对应的服务水平系数; T 为提前期,即连续向灾区供应物资的间隔期;
为在服务水平 ϕ 的基础上,对应的服务水平系数; T 为提前期,即连续向灾区供应物资的间隔期; 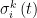 为受灾区域 i 在时刻 t 对应应急物资 k 的单位时间平均需求量的标准差;
为受灾区域 i 在时刻 t 对应应急物资 k 的单位时间平均需求量的标准差; 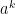 为受灾人口单位时间对应应急物资 k 的需求量;
为受灾人口单位时间对应应急物资 k 的需求量; 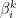 为灾区 i 内应急物资k 的存储量;
为灾区 i 内应急物资k 的存储量; 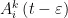 为时间段(t-ε)内物资 k 送达灾区 i 的数量;
为时间段(t-ε)内物资 k 送达灾区 i 的数量; 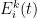 为t时刻向灾区 i 供应物资 k 的数量;
为t时刻向灾区 i 供应物资 k 的数量;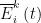 为
为 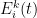 的均值[14]。因此,震后应急物资需求模型构建如下:
的均值[14]。因此,震后应急物资需求模型构建如下:
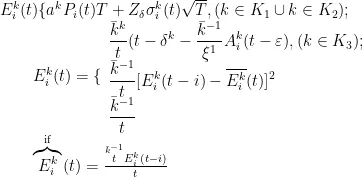
4.3 实例分析
本文采用2023年甘肃省夏州市积石山县的地震灾害数据作为实验数据,并进行此次地震各类应急物资需求量的预测。该地震灾害数据如表3所示。
 表3地震灾害数据
表3地震灾害数据结合应急物资需求估算公式,设定相关参数如表4所示。
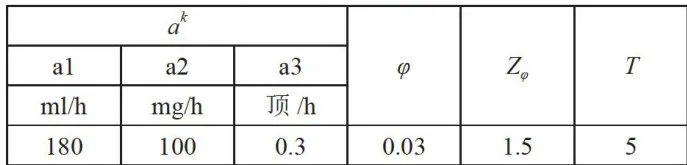 表4安全库存理论相关参数设置
表4安全库存理论相关参数设置
基于博弈论-SAGA-AHP特征权重优化算法的CBR预测受灾人口数量,经式(1)和MATLAB编程计算得到目标案例与历史案例的全局相似度,选取相似度最高的历史案例27,相似度为0.995,因此预测目标案例积石山县震后受灾人口数量为143359人,与实际受灾人数152853人相近,相对误差(MRE)为 6 . 2 1 % ;基于构建的震后应急物资需求预测模型,计算得到此次地震所需要的各类别应急物资的需求量。在震后初始时刻,即 t = 0 时, 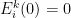 ,其第一时间段的预测结果如表5所示。
,其第一时间段的预测结果如表5所示。
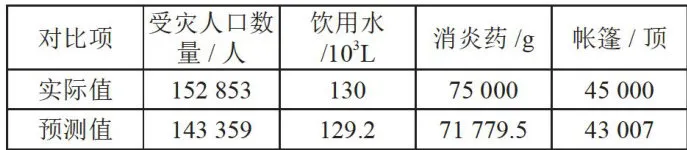 表5预测结果
表5预测结果5结论
本文提出了基于博弈论-SAGA-AHP特征权重优化算法进行案例推理法的改进,将影响震后受灾人口数量的7个关键因素设为预测模型的特征属性,提取相似度最佳的历史案例并辅以专家修正对震后受灾人口数量进行预测,并基于受灾人口数量与各类应急物资需求之间的关系,构建震后各类应急物资需求量的预测模型,应用于震后应急物资需求的预测。研究结果表明,基于博弈论-SAGA-AHP的特征权重优化算法融合了主、客观赋权的优点,解决了GA算法容易陷入局部最优的问题,与GA、SAGA算法相比,能够显著提高案例推理法的预测精度。
参考文献:
[1] ZHOUL,WUXH,XU Z S,et al.EmergencyDecision MakingforNaturalDisasters:An Overview-ScienceDirect[J].International Journal ofDisaster Risk Reduction,2018,27:567-576.
[2]ZARGHAMISA,DUMRAKJ.ASystemDynamicsModelforSocialVulnerabilitytoNaturalDisasters:DisasterRiskAssessment of an Australian City[J].International Journal ofDisasterRiskReduction,2021,60:102258.
[3] HUANG D,WANG SA,LIU ZY.A SystematicReviewof Prediction Methods forEmergency Management[J].InternationalJournalofDisasterRiskReduction,2021,62:102412.
[4]李云松,张智晟.考虑综合需求响应的Transformer-图神经网络综合能源系统多元负荷短期预测[J].电工技术学报,2024,39(19):6119-6128.
[5]亢丽君.粒子群优化BP神经网络在应急物资需求预测中的应用研究[D].兰州:兰州交通大学,2013.
[6]程琼琼.基于GA的BP神经网络的地震应急物资需求预测[D].成都:西南财经大学,2016.
[7]王庆荣,马辰坤.面向案例消耗推理的应急物资预测[J].计算机工程与应用,2021,57(22):281-287.
[8]LI R.Research on Emergency Supplies DemandForecastingModel[C]//2010 the 2nd International ConferenceonIndustrialMechatronicsandAutomation.wuhan:IEEE,2010:244-247.
[9]ZHANG HQ,XUJY.Research on Emergency MaterialDemandForecastingModel inDisasterBasedonMLR-CBR[C]//International ConferenceofLogisticsEngineeringamp;Management.[S.I],2010,387:2888-2894.
[10]ZHOUM,LIUXB,CHENYW,etal.AssignmentofAttributeWeightsWithBeliefDistributionsforMADMUnderUncertainties[J].Knowledge-Based Systems,2020,189:105110.
[11]PHANAV,NGUYENML,BUILT.FeatureWeightingand SVMParametersOptimizationBasedonGeneticAlgorithms for Classification Problems [J].Applied Intelligence,2017,46:455-469.
[12]童文林,陈德旺,黄允浒,等.结合模拟退火与规则约简的模糊系统优化方法[J].计算机工程与应用,2021,57(16):142-150.
[13] TASKINS,JREJL.ABayesianDecisionModel withHurricane Forecast Updates for Emergency Supplies InventoryManagement [J].Operational Research forEmergency PlanninginHealthcare,2016,1:330-352.
[14]SHEU JB.An emergency logistics distributionapproach for quick response to urgent reliefdemand in disasters[J].Transportation Research PartELogisticsamp; TransportationReview,2007,43(6):687-709.
作者简介:周湛赞(1995一),男,汉族,湖南岳阳人,
工程师,硕士研究生在读,研究方向:深度学习、数据处理。