基于数据挖掘的移动通信客户流失预测模型研究与应用

张驭思

（上海理工大学，上海 200093）

我国网络建设正处于快速发展阶段，通信行业信息量和业务收入均迎来指数级别的增长，通信运营商的经营重点正逐渐从产品/服务向维持客户资源转变。研究表明，通信行业发展新客户比维持现有客户的平均成本高出5倍以上，而且现有客户流失会降低企业的社会满意度和信赖度等诚信指标，严重影响企业的进一步发展。因此，与客户保持良好关系，预防客户流失，维持现有客户资源有助于进一步获得市场竞争优势。准确、高效的客户流失预测模型能够对现有客户潜在的离网行为进行合理预测，使运营商及时调整相应的营销策略进行挽留，对加强企业用户关系管理（Customer relationship management, CRM）具有十分重要的意义。

近年来，基于数据挖掘技术的CRM应用研究获得了国内外中大型企业及金融机构的广泛关注，在用户关系管理、金融欺诈检测方面获得了显著的成果。相比于传统的计算方法，数据挖掘能够从大量的实际数据中挖掘出对决策具有参考价值的隐含关系和趋势，进而为决策过程提供相应的支持。通过数据挖掘技术对客户某一时间段的行为特性进行分析，能够获取相应的行为习惯及兴趣爱好，进而给予客户针对性服务，提升企业用户黏度。从统计学的角度出发，客户流失预测模型的输出属于典型的二分类问题，即结果只有流失（用“1”表示）与非流失（用“0”表示）两种可能，目前主要存在三种预测模型：单一分类模型，如决策树、逻辑回归及关联性分析等；聚类分析模型，如K-means聚类、Two-step聚类等；多分类模型融合，如采用Bagging、Stacking方法对多类单一分类模型进行集成。Kim团队采用逻辑回归模型对韩国移动通信用户数据进行建模，通过流失客户特性分析，对现有客户忠诚度进行评分，实现对现有客户的分类化管理。贺建军对支持向量机（SVM）在预测客户流失方面的适用性进行了分析，分别从实验和理论角度验证了该模型的预测精度。曹国团队采用二元逻辑归回对某商业银行用户流失情况进行分析，建立了客户流失多维预测指标，通过模型分析和实证研究发现交易频率、客户年龄、近期交易记录等因素对客户流失有十分显著的影响。武彩霞团队基于数据挖掘提出多分类融合模型应用于通信企业用户流失管理系统，通过对客户流失数据集的训练分析，表明多模型预测准确度高于普通的单一模型。

上述研究构建的客户流失预测模型对企业的精细化运营管理具有十分积极的推动作用，降低了客户流失比例和企业运营成本，但对于用户特征分析和数据挖掘技术缺少系统的融合。本文以通信运营商对现有客户流失管理为主题，以高效预测客户流失为目的，采用Python语言为编码工具，通过对一元、多元逻辑回归和神经网络模型进行建模，并对模型预测效果进行系统对比分析，获得更适宜移动通信运营客户流失的预测模型；将统计学理论、数据挖掘技术融入金融管理理论，实现多学科交叉融合，给通信运营行业解决用户流失问题和构建个性化用户运营机制提供了一定的参考价值。

本文实验的原始数据来源于某电信部门数据库，构建模型之前，需要对原始数据进行初始选择、数据清洗、数据整合与构建，最后按照既定标准进行格式化，本文从客户信息到行为因素等多个分析维度来综合衡量各类变量特征对客户流失的影响，初步确定17项指标，如表1所示。

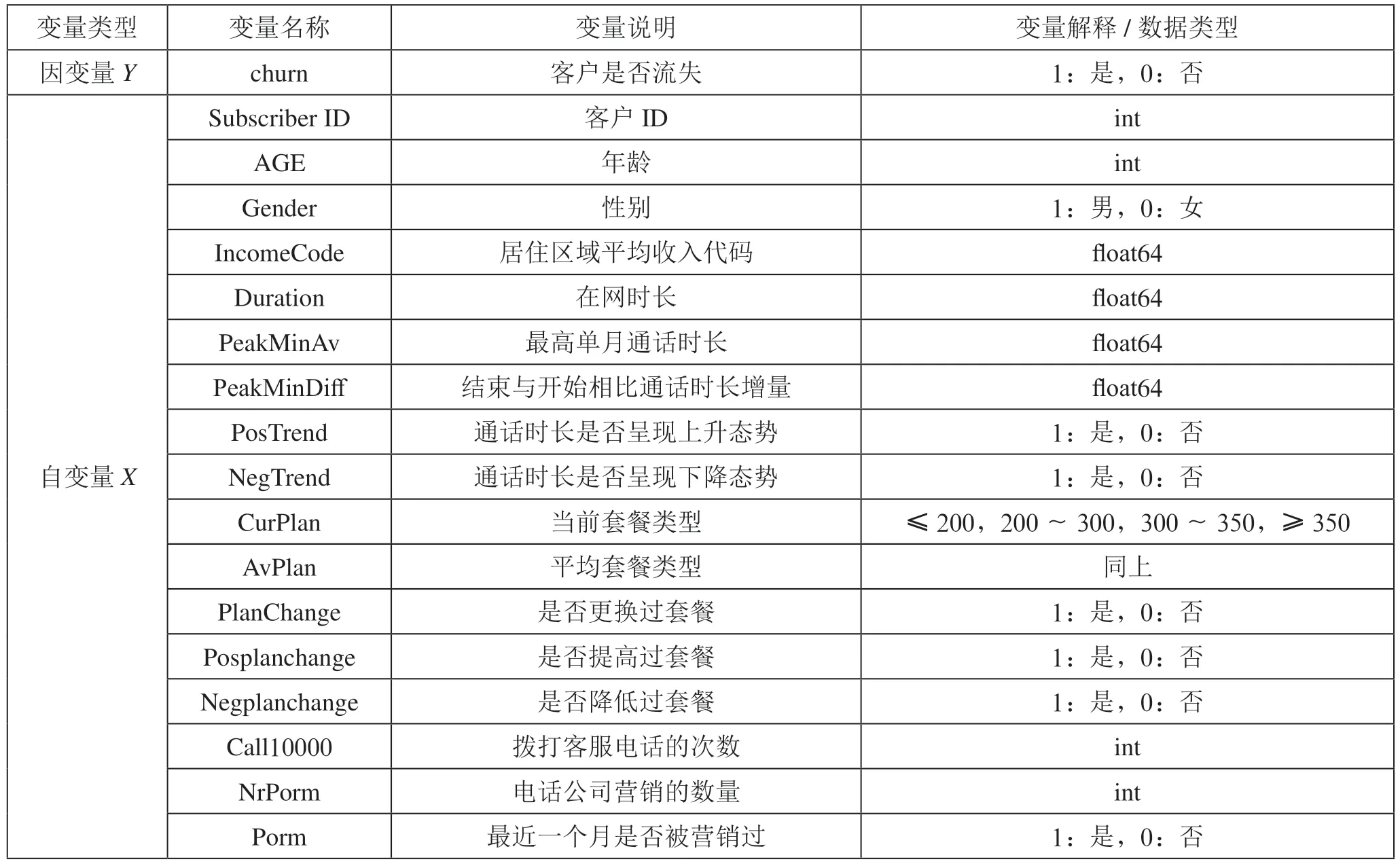
表1 通信客户流失模型变量

自变量中共有6个分类变量，采用交叉表分析和卡方检验判定这类变量与目标变量的相关性。篇幅所限，本节仅展示通话时长是否呈现下降态势（NegTrend）与客户流失（churn）的相关性分析，结果如图1所示，从交叉表可以看出，在流量使用有下降趋势时，客户流失的概率会上升，从对应的卡方检验p-value可以看出，NegTrend这一变量与的相关性非常显著（＜0.000 1），说明该变量具有分析价值，其他变量均按照上述检验流程进行。

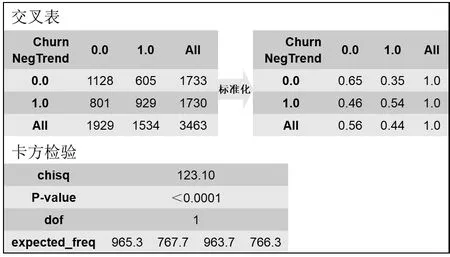
图1 交叉表/卡方检验分析

关于连续型自变量有多种相关性检验分析方法，例如分层抽样、假设检验、方差分析等，鉴于本文涉及的自变量较少（＜20），采用逻辑回归的逐步向前分析较为合理。随后采用方差膨胀因子检测的方式对自变量间多元共线性问题进行检测，将VIF值大于10的变量进行筛选，最终确定10个特征作为后续模型的自变量，如表2所示。

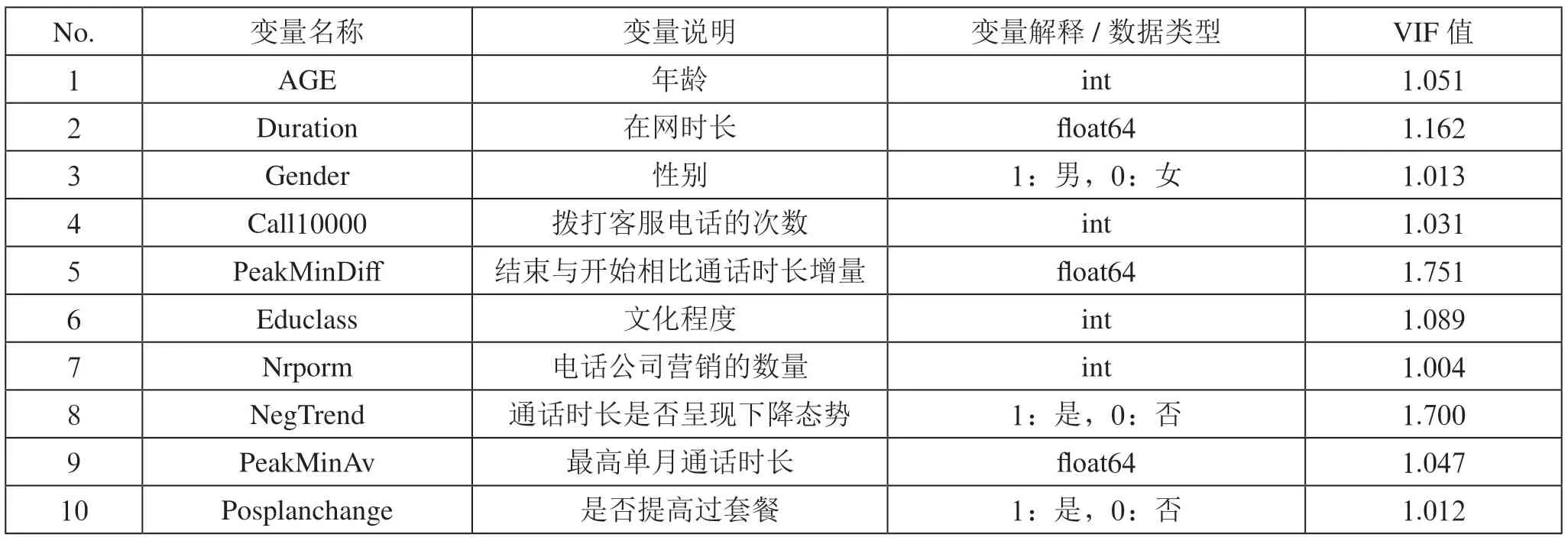
表2 筛选后的自变量

1.3.1 逻辑回归

逻辑（Logistic）回归是针对二分类问题构建的非线性归回模型，本质上属于广义多元线性回归。我们希望获得用户流失的概率，这一数值应介于0和1之间，显然线性回归难以描述与自变量间的关系，需要一个严格单调的函数（），满足在接近0和1两个端点时（）会产生敏感且显著的变化，即Logit变换：

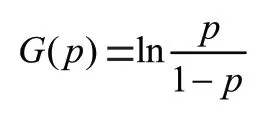
可以看出，在0～1之间变化时，对应的（）变化范围为（-∞，+∞），解决了与之间的非线性问题。值得注意的是，区别于线性回归，逻辑回归并不是通过最小二乘法来进行模型的优化，根据其变换的非线性特性选取极大似然估计方法确定回归系数更为合理。

1.3.2 人工神经网络

人工神经网络（Artificial neural network, ANN）是通过数据样本进行训练从而实现对相关信息处理功能的一类预测模型，不需要任何先验公式，具有极好的自适应、并行处理和非线性转换能力，对于正态、随机分布的数据都可以采用ANN进行分析，做出合适有效的预测。本文构造的人工神经网络结构及计算流程如图2所示。

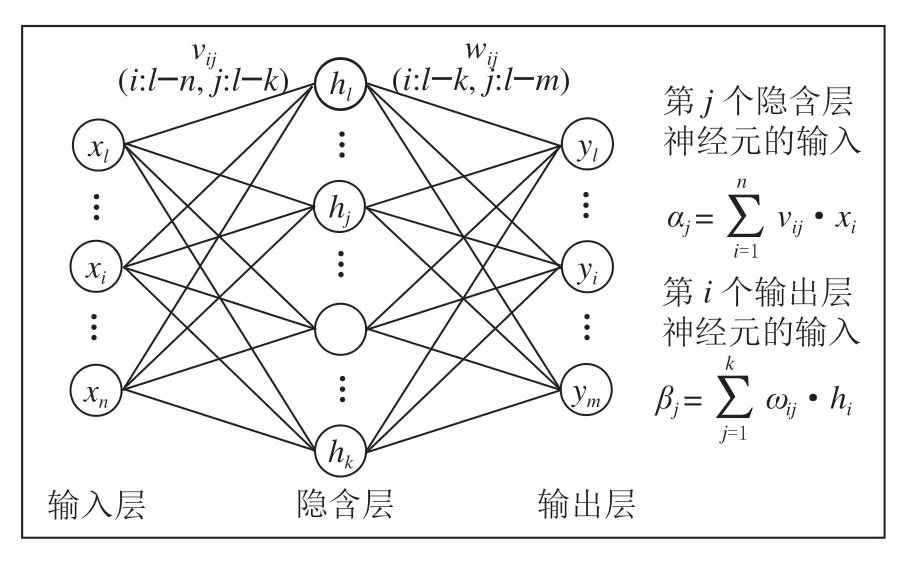
图2 ANN结构及流程图

图中每一个节点作为神经元接收并处理上层节点的信息，其中输入层中的神经元即为自变量，神经元数量和自变量数量相同；而中间隐含层的神经元接收来自每个输入层神经元信息的线性组合，并通过自身设置的激活函数对输入信息进行转换，类似于逻辑回归中→（）的处理，因此神经网络在某种意义上可以看作逻辑回归的扩展。在模型优化方面，Loss函数可以选择用最小二乘法表示，优化方式采用梯度下降，不断优化权重和，直至误差降至可接受的范围内，模型训练完成。

建模之前，需要将数据分为训练集和测试集，前者用于训练模型，后者用于评估模型的预测表现及准确性，本文将训练集和测试集的比例定为8：2。从图3可以看出因变量的数据分布并不平衡，但在可接受的范围（44%～56%）内，考虑到实验数据量不大，为保证预测模型的精确度，本文不进行数据平衡处理，从数据集中随机抽取80%（样本量：2 772）作为训练集，剩余20%（样本量：692）作为测试集。

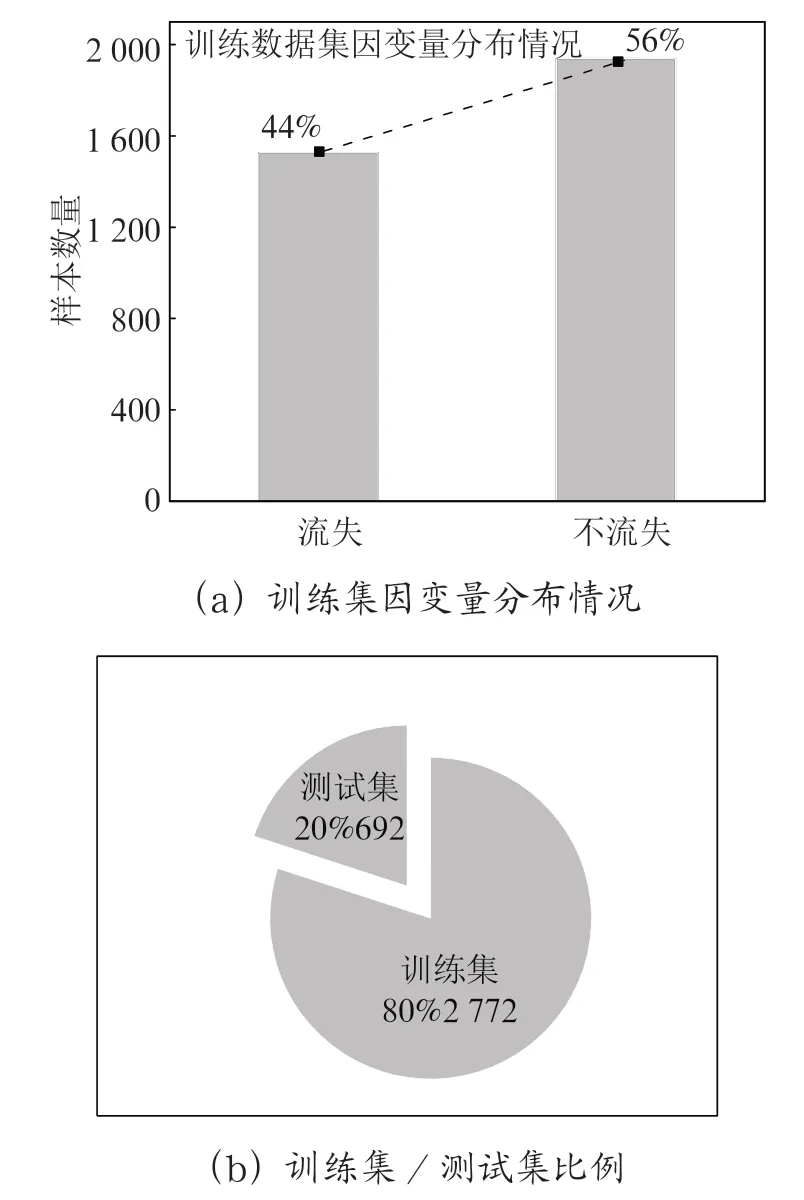
图3 数据集变量分布及训练集/测试集分布

本文实验在Windows10操作系统环境下，采用Spyder编辑器结合Python语言，并利用机器学习库Sklearn、Pytorch、statsmodels构建逻辑回归和神经网络模型，硬件条件为8核8线程3.60 GHzCPU，RAM 64 GB。

我们将相关性检验后的10个自变量（表2所示）作为特征向量，进行逻辑回归训练，获得各变量的权重估计，如表3所示。

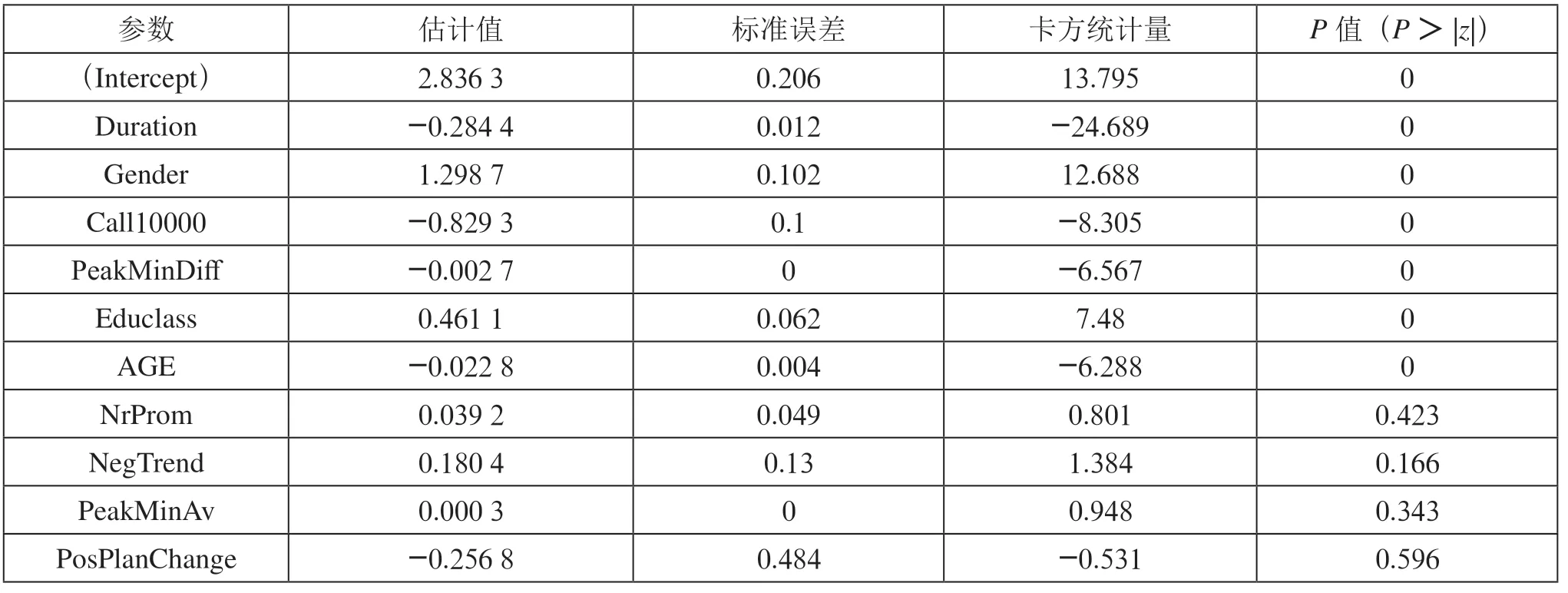
表3 逻辑回归模型权重估计

可以看出在10个因子中，用户性质（gender）、受教育程度（Edu_class）、营销频次（Nrporm）、用户通话时长变化（NegTrend）、单月最高通话时长（PeakMinAv）对客户流失具有正向影响；而在网时长（Duration）、联系客服频次（Call10000）、通话时长增加量（PeakMinDiff）、年龄（AGE）、是否提升过套餐类型（PosPlanChange）对客户流失具有反向影响，即这五项变量数值越大，用户越不容易流失，其中联系客服频次对该模型影响最大，可以认为联系客服越频繁的客户流失的概率越低。获得各变量对应的估计值后，可以建立的流失模型（LossTrend）方程为：

本文采用常规三层神经网络模型，即一个输入层、一个隐含层和一个输出层，输入层神经元个数为10个，对应10个自变量。对于二分类问题，输出层神经元个数为2个，只有隐含层神经元的数量需要进一步讨论，数量范围由以下公式得出：

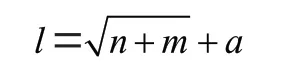
其中、、分别为隐含层、输入层和输出层神经元个数，为调节因子，取值范围[1-10]，初步确定该神经网络模型l的取值范围为[4-14]。将训练次数定为500次，获得l取不同数值对应的模型预测准确率AUC结果，如图4所示。

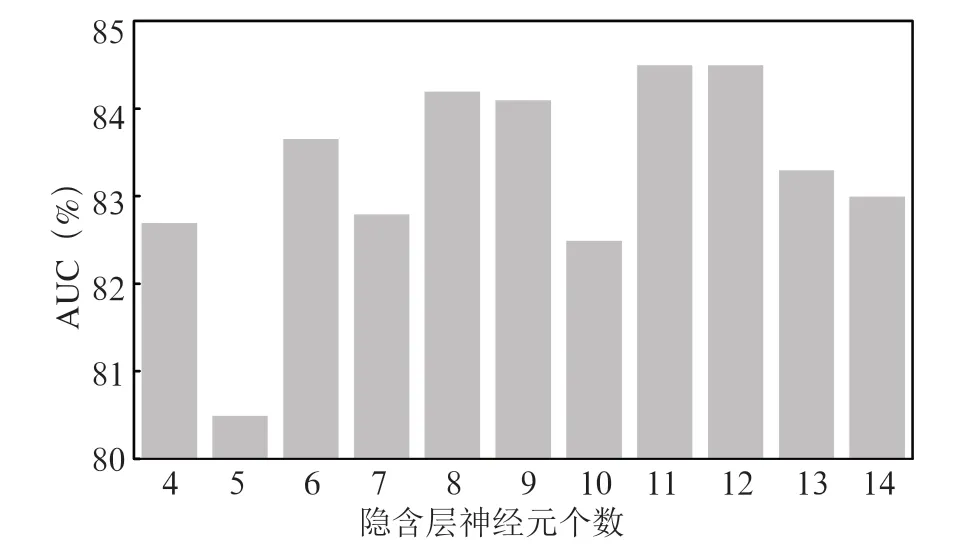
图4 预测结果随隐含层神经元数量变化情况

可以看出，隐含层神经元个数为12时，AUC值最大，此时模型预测效果更好，因此本文将隐含层单元数量确定为12个，同时将最大训练次数扩大至1 000次，激活函数选用Sigmod函数，学习率为0.001。至此，本文神经网络框架已构建完成，权重更新方式（即模型优化方法）采用比经典随机梯度下降法更为高效的Adam优化算法。

2.4.1 混淆矩阵评估

混淆矩阵是评价二分类模型最常用的手段，将预测值和真实值作比较，可以输出表4所示的矩阵。

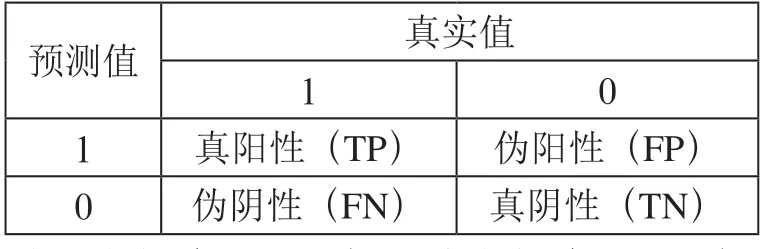
表4 混淆矩阵

通过准确率（Accuracy）、精确率（Precision）、召回率（Recall）、提升系数（Lifting）和F1系数共5项指标对预测结果的准确和稳定性进行评估。相关公式为：

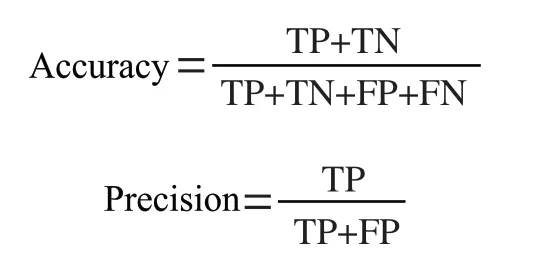
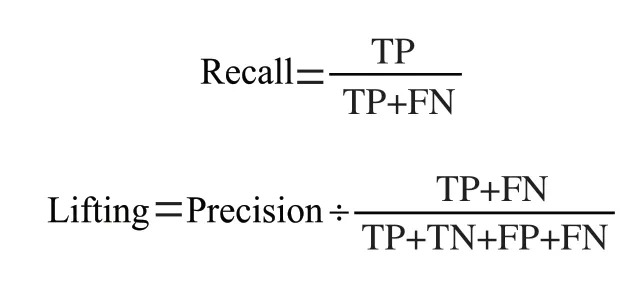
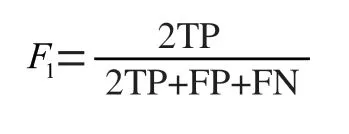
通过对逻辑回归和神经网络模型的混淆矩阵进行分析，可以分别求出上述5项指标，结果如表5所示。

表5 两种模型预测效果对比

可以看出，神经网络具有更好的预测效果，在流失客户样本的预测正确率方面神经网络比逻辑回归高出2%，表明在判断客户是否为流失客户方面，神经网络的预测结果更为准确；从召回率来看，在实际流失客户的样本正，神经网络也具有更高的预测比例，在提升系数和F1值上也有更好的表现。

2.4.2 ROC曲线评估

ROC曲线可以反映预测模型和分析方法敏感性与特异性间的关系，横纵坐标分别代表正例的错误命中率（FPR＝FP/（FP＋TN））和正例的预测准确率（TPR＝TP/（TP＋FN）），曲线和横轴间的面积为AUC值，该数值越接近1模型的预测效果越好。本文分别绘制逻辑回归模型和神经网络模型的训练和测试ROC曲线，并列出对应的AUC值，如图5所示。

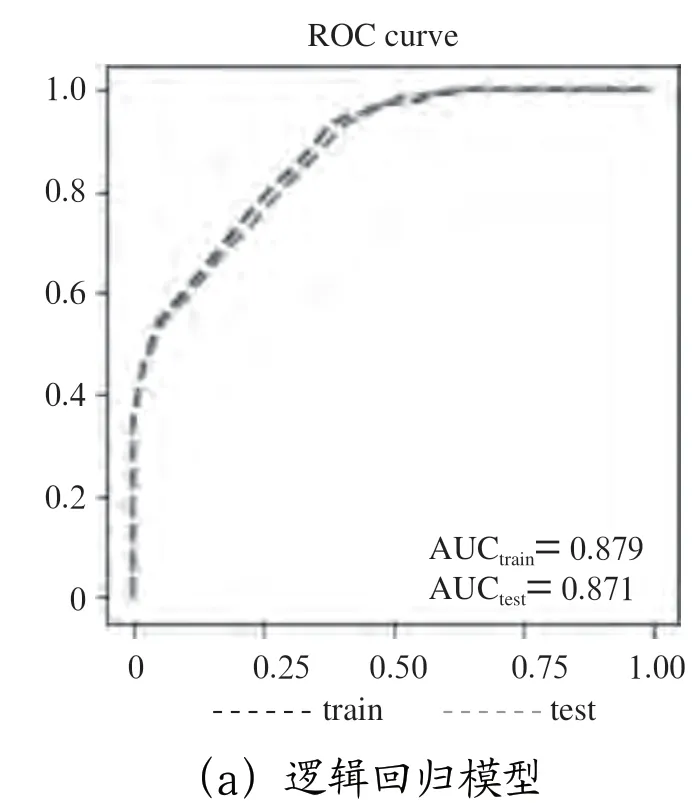
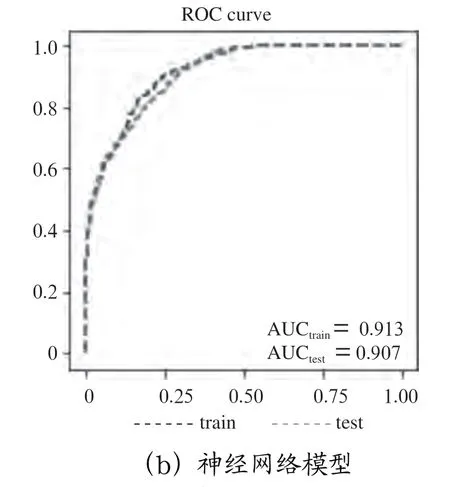
图5 逻辑回归和神经网络模型ROC曲线

可以看出无论是逻辑回归还是神经网络，测试集的结果均和训练集结果相差不大，说明本文构建的两种模型没有明显的过拟合现象，预测的结果合理且可靠。

从模型精度而言，神经网络模型的测试和训练集AUG值均在0.9以上，高于逻辑回归模型，说明神经网络精度更高。

综上所述，结合混淆矩阵和ROC曲线评估结果，可以认为本文所构建的两个模型在可靠性和精确度上均具有良好的表现，相比而言，神经网络更具优势。

完成模型的构建和可靠性分析之后，将模型正式嵌入数据平台，对未来流失用户进行实时预测，定期生成流失预警名单，结合运营部门和策略部门制定有针对性的挽留方案，实现客户流失前期运营，提高挽留成功的概率。具体嵌入模块及流程如图6所示。

图6 模型嵌入模块及应用流程图

首先，利用问卷调研、平台抓取等手段结合互联网大数据系统获取客户实时的行为数据，存入数据仓库并进行定期整理、清洗和格式化处理，提升数据的整洁性，进入基于神经网络的客户流失预测模型进行计算，将结果输入运营管理系统，根据客户特征进行有效分类并制定有针对性的挽留策略，当客户触发流失条件时系统自动根据客户类别进行针对性挽留。通过数据分析归纳，不断优化模型和实施流程。

本文以通信运营商对现有客户流失管理方法为研究对象，结合金融管理、统计学理论和数据挖掘建模手段建立了针对通信客户的流失预测模型，针对移动通信用户流失问题进行了定量分析。通过不同模型运行结果对比分析，发现本文构建的人工神经网络模型比传统的逻辑回归模型在各项评价指标上均有较强的优势，同时将模型嵌入管理模块并提出对应的运营系统及流程，这对企业客户服务平台和运营管理优化改进具有重要的指导意义。