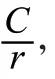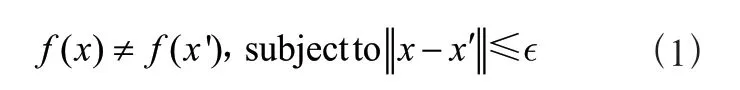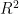
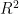
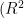
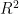
天键词:涡流管;预测模型;混合神经网络;温度性能中图分类号:TP183;TP399 文献标识码:A文章编号:2096-4706(2025)08-0194-05
Abstract: Inthis paper,a hybrid neural network model is constructed by adding the physical constraint conditions of theBernoulliequationandtheNicolas formula,exploringthetemperaturechangelawof thecoldendofthevortex tubeand making corrsponding predictions.The network adoptsa multi-layer fedforward model andthe Levenberg-Marquardt learning algorithm,andtehypebolictangentfunctionisselecedasthetransferfuncion.Inadditio,thecofcientofdeteation 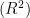 and the Root Mean Square Eror (RMSE)areused to determine the statistical validityof the developed model,and he models uncertainty and robustness are analyzed.The hybrid model has an index
and the Root Mean Square Eror (RMSE)areused to determine the statistical validityof the developed model,and he models uncertainty and robustness are analyzed.The hybrid model has an index 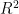 of 0.9936and anRMSEof0.3392,and also has agood performance in tersofuncertaintyand robustnessThesedata indicate thatthe modelconstructed in this paper successfully predicts the changes in the temperature of the cold end of the vortex tube and has good accuracy.
of 0.9936and anRMSEof0.3392,and also has agood performance in tersofuncertaintyand robustnessThesedata indicate thatthe modelconstructed in this paper successfully predicts the changes in the temperature of the cold end of the vortex tube and has good accuracy.
Keywords: vortex tube; predictive model; hybrid neural network; temperature performance
0 引言
涡旋管又称为Ranque-Hilsch管(RHVT),其是一种简单的装置,由一根简单的圆形管、一个或多个切向喷嘴、冷端孔和一个热端控制阀组成(如图1所示)。压缩气体通过RHVT入口进入管内,经过涡流管独特的温度分离效应,最终被分离成两股温度不同的流体。涡流管因其结构简单、体积小、重量轻、成本低、不用电、不使用化学品、运行时间长等优点,已广泛应用于众多领域[1。但RHVT仍存在一些不足。目前限制涡流管大规模应用的主要原因是其效率低。涡流管在控制冷却、加热和分离等方面的优势对实现减排和降低成本具有重要意义,通过优化提高其性能,促进该便捷装置的更广泛应用对现实社会具有重要的效益。涡流管的优化主要是对其温度分离过程进行研究,但涡流管的温度分离过程非常复杂,诸多因素如喷嘴形状、喷嘴数量、涡流管直径和长度、进口压力等都对涡流管的温度分离过程有着影响。
 图1涡流管结构示意图
图1涡流管结构示意图
为了提高涡流管的性能,许多学者通过各种方法对涡流管的几何参数和工作参数进行了优化研究。应用最广泛的技术是控制变量法,即在保持其他参数不变的情况下,通过改变单个几何参数或操作参数来寻求最优参数,从而得到最优参数的经验总结。例如,ParkerMarkya等[研究了压力大小、压降和压比对涡流管进出口温度的影响,研究结果表明,压力比为2.0时,最大恢复温度降为 1 3 . 9 6 K ,对应的静态温度降为 1 2 . 2 5 K 。Attalla等[3]研究了喷嘴数量对涡流管冷却性能的影响。喷嘴数量选择了2,3,6。结果表明喷嘴数量为3个时,涡流管的冷却性能最佳。Avcl4通过实验研究了喷嘴展弦比(0.25,0.44,0.69)和喷嘴数量(1,2,3)对涡流管性能的影响.结果表明,单喷嘴涡流管的性能优于双喷嘴和三喷嘴涡流管。Rafiee等[研究了导航角( 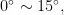 )对能量分离和内部气流速度变化(旋流和轴流)的影响。发现:当导航角为
)对能量分离和内部气流速度变化(旋流和轴流)的影响。发现:当导航角为 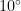 是涡流管冷却和加热能力最好,其轴向速度和漩涡速度下降的最快。
是涡流管冷却和加热能力最好,其轴向速度和漩涡速度下降的最快。
在涡流管性能研究中,神经网络被用于建立模型、预测流体特性和管道行为。神经网络能够通过训练来理解和预测复杂的非线性关系,有助于分析涡流管内的流体行为、温度分布和压力变化。它们可以用于模拟不同条件下的流体流动,帮助工程师理解和优化涡流管设计以及流体传输过程。因此,许多学者开始使用神经网络来研究涡流管特征参数对其性能的影响。Pouraria等以遗传算法寻找到的最优网格结构构建成了人工神经网络,随后以涡流管的长径比,进口压力,冷质量分数,冷端直径与管径之比为参数对涡流管冷却性能进行建模。结果表明:基于遗传算法的人工神经网络模型可以在较宽范围内预测涡流管的冷却性能。
Kaya等[通过新框架使ANN模型具有可推广性和鲁棒性。以喷嘴材料(导热系数);喷嘴数量;入口压力为输入参数,总温差为输出参数来训练模型。训练后的模型的决定系数 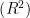 ),后误差率 ( C ) ,平均绝对百分比误差(MAPE)分别为0.9878,0.19,0.0671。Kaya8应用线性、KNN、RF、SVM四种方法对工作流体为氮气的涡流管热性能进行实验研究。结果表明在上述四种方法中SVM回归方法的效果最好,精度为 9 6 . 0 1 % 。Pouraria等[以遗传算法寻找到的最优网格结构构建成了人工神经网络,随后以涡流管的长径比,进口压力,冷质量分数,冷端直径与管径之比为参数对涡流管冷却性能进行建模。结果表明:基于遗传算法的人工神经网络模型可以在较宽范围内预测涡流管的冷却性能。
),后误差率 ( C ) ,平均绝对百分比误差(MAPE)分别为0.9878,0.19,0.0671。Kaya8应用线性、KNN、RF、SVM四种方法对工作流体为氮气的涡流管热性能进行实验研究。结果表明在上述四种方法中SVM回归方法的效果最好,精度为 9 6 . 0 1 % 。Pouraria等[以遗传算法寻找到的最优网格结构构建成了人工神经网络,随后以涡流管的长径比,进口压力,冷质量分数,冷端直径与管径之比为参数对涡流管冷却性能进行建模。结果表明:基于遗传算法的人工神经网络模型可以在较宽范围内预测涡流管的冷却性能。
目前将物理规律与神经网络结合的研究被应用到各种不同的领域:Li等提出了一种混合方法,将物理模型与连续时间状态空间神经网络结合,用于更精确地分析复杂结构系统。Zheng等[10开发了一种结合物理模型与BP神经网络的模型,用于预测模拟煤矿环境下腐蚀污染物的强度衰减,旨在更准确地评估混合腐蚀对污染物结构性能的影响。Xiao等[1利用物理信息神经网络(PINN)改进来雷诺平均纳维-斯托克斯(RANS)模型对瑞利-泰勒湍流混合现象的模拟,通过将物理规律碱性神经网络,提高了对复杂湍流流行为的预测的准确性。Wen等[12]提出了一种结合网络与物理模型的混合方法,用于更准确地预测土壤中的反应前沿位置及其动态变化。通过融合数据反应神经驱动与物理模型,该研究改进了土壤化学过程的模拟能力。
涡流管因其特殊的温度分离现象而被应用到众多领域,其冷端低温效应可以应用在需要低温环境的工作中,但涡流管与物理模型相结合的相关研究有所不足。本文首次通过引入基于伯努利方程和尼古拉兹公式作为物理约束条件来构建物理-神经网络混合模型来预测涡流管的性能参数。通过这一模型的建立,本文不仅为涡流管性能参数的预测提供了新的工具,也为物理与神经网络相结合的建模方法在复杂工程问题中的应用开辟了新的路径。
1模型的构建
在本研究中,采用混合模型对涡流管的冷端温度性能进行建模。为了估计出口温度的输出值,我们训练了一个采用Levenberg-Marquardt反向传播算法的多层前馈网络。使用的人工神经网络结构如图2所示。隐藏层一共有两个层次的11个神经元,输入参数为进口压力 ( P ) ,冷质量分数 ( ζ ) ,入口温度( 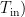 。输出层为涡流管冷端温度(
。输出层为涡流管冷端温度( 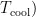 。
。
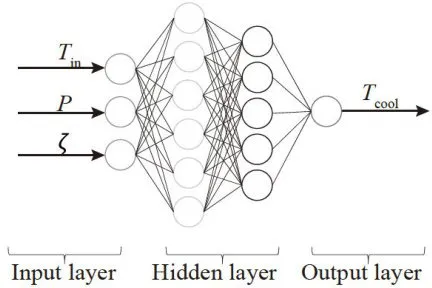 图2提出的混合神经网络模型
图2提出的混合神经网络模型模型的训练,预测,验证样本分别占总样本的70 % , 1 5 % , 1 5 % 。所有的数据在使用前已经进行了打乱。混合网络的训练速度和错误率分别为0.1和0.00001。在对数据应用混合神经网络之前,对训练输入和输出值进行归一化。
模型的评估指标选择RMSE和 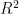 。其中RMSE是用来衡量模型预测值和实际观测值之间差异的一种常用的指标。在神经网络中RMSE的值越小,表示模型的预测效果越好。
。其中RMSE是用来衡量模型预测值和实际观测值之间差异的一种常用的指标。在神经网络中RMSE的值越小,表示模型的预测效果越好。 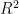 提供了模型中再现的数据的可变性度量。
提供了模型中再现的数据的可变性度量。 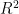 的值越接近1表示模型可以很好地解释观测值的变异,模型拟合效果越好。如图3所示,图3为预测
的值越接近1表示模型可以很好地解释观测值的变异,模型拟合效果越好。如图3所示,图3为预测 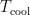 的训练过程中各步骤得到的线性相关系数R。整个网络的 R 值在所有步长都保持在0.90左右,这表明整个模型与所选输入达到了可接受的拟合。
的训练过程中各步骤得到的线性相关系数R。整个网络的 R 值在所有步长都保持在0.90左右,这表明整个模型与所选输入达到了可接受的拟合。
 图3由混合神经网络模型得到的线性回归系数用于估计冷出口温度
图3由混合神经网络模型得到的线性回归系数用于估计冷出口温度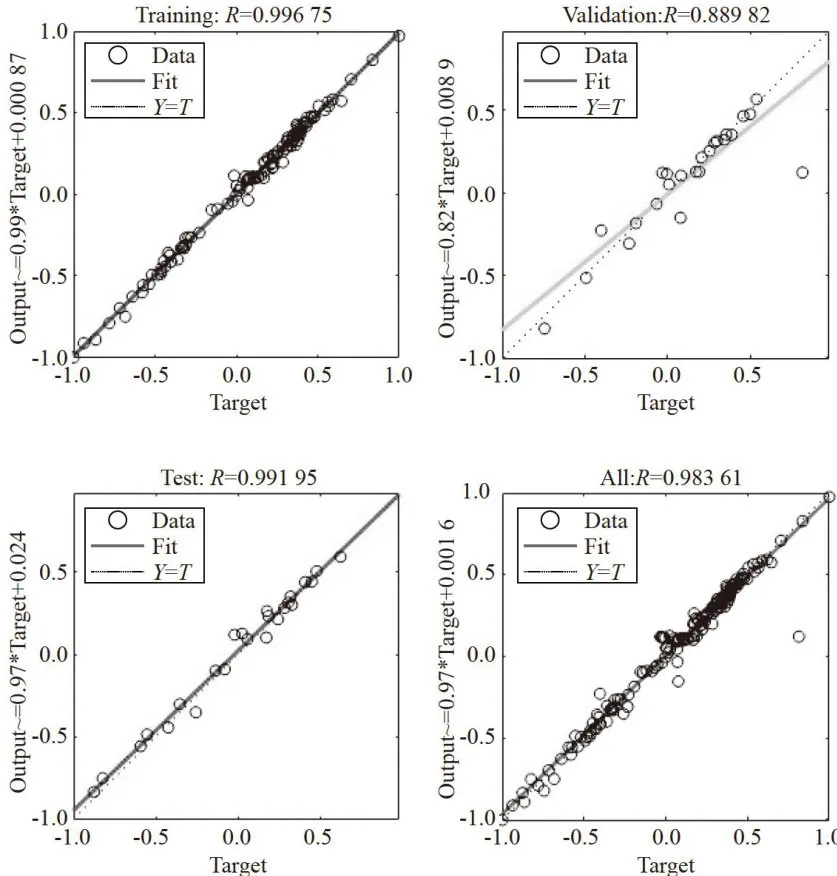
2 结果与讨论
2.1 模型的性能分析
在本研究中,我们首先构建并训练了一个原始神经网络模型,随后对其进行了改进,通过引入伯努利方程和尼古拉兹公式作为物理约束条件,将其转化为物理-神经网络混合模型。为了确保对比的公平性,两个模型均使用相同的数据集和网络结构进行训练模拟,并采用1000次迭代以保证训练的充分性。
模型性能的对比如表1所示。从表中数据可以看出,添加物理约束条件的物理-神经网络模型在性能指标上显著优于原始神经网络模型。具体来说,添加物理约束后,模型的决定系数 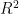 有所提升,表明预测值与真实值之间的拟合效果更好;均方根误差(RMSE)则明显降低,显示出模型预测的误差更小。这些改进表明,物理约束条件的引入能够有效提升模型的预测能力。
有所提升,表明预测值与真实值之间的拟合效果更好;均方根误差(RMSE)则明显降低,显示出模型预测的误差更小。这些改进表明,物理约束条件的引入能够有效提升模型的预测能力。
 表1模型性能结果
表1模型性能结果2.2 不确定度分析
本研究采用基于Dropout的近似贝叶斯方法来对本文构建的模型进行不确定性分析。通过在每个隐藏层添加Dropout层来使隐藏层在训练时随机丢失部分神经元节点的方法来避免模型过度拟合。如图4所示,图4为模型不确定分析误差条图,从图中可以看出大部分数据点都分布在一条直线附近,这表明模型的预测非常接近真实值,模型拟合程度好;数据点上的误差条反映了模型的预测不确定性,从图中可以看出所有数据点对应的误差条都较短,这表明模型对该点的预测更为确定;但是仍有几个数据点偏离直线,这可能代表着模型在特定输入上存在偏差。模型的预测平均值和 9 5 % 置信区间如图5所示,从图中可以看出大多数真实值都可以被 9 5 % 的置信区间覆盖,这说明模型在大多数情况下可以给出合理的预测区间,总体来说,模型可以准确地估计预测值的不确定性;但是从图中可以看出有几处波动点未能被覆盖,这表明模型在某些情况下的预测不确定性评估可信度较低。
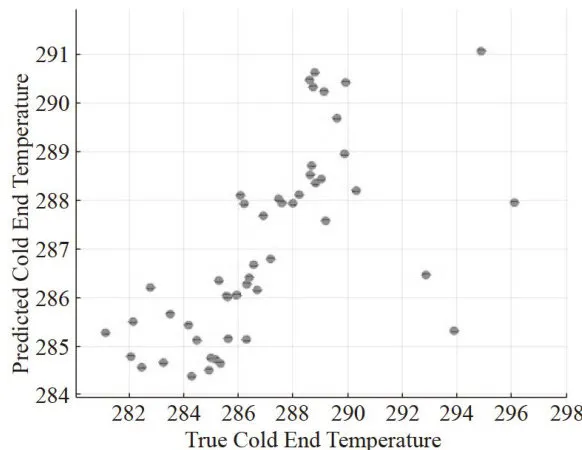 图4模型不确定度误差条图
图4模型不确定度误差条图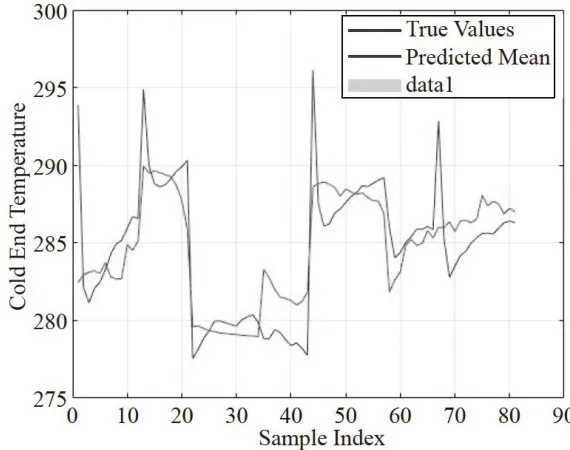 图5模型不确定度预测平均值和 9 5 % 置信区间
图5模型不确定度预测平均值和 9 5 % 置信区间2.3 鲁棒性分析
模型预测值与真实值的对比情况如图6所示。从图中可以着出,模型的预测值与真实值高度接近,大部分数据点分布在接近理想状态的对角直线附近。这表明模型具有较强的鲁棒性,在大多数输入值范围内能够实现稳定且准确的预测。然而,图中也出现了一些明显的异常值,说明模型在特定条件下仍存在一定的不足之处。这些异常值可能源于数据的噪声、不充分的物理约束或模型结构的局限性,提示未来需要对模型进行进一步优化和改进。
总体而言,以伯努利方程和尼古拉兹公式为物理约束条件构建的物理-神经网络模型,在预测精度和鲁棒性方面表现出良好的性能。这种结合了物理规律的建模方法,不仅能更好地描述涡流管的复杂物理行为,还为解决其他复杂物理问题提供了参考价值。未来,通过进一步优化模型的物理约束条件和算法设计,有望进一步提升模型的适用性和预测精度。
从分析结果可以看出,添加了物理约束的物理信息神经网络(PINN)模型不仅仅依赖于对数据的简单拟合,还能够有效地结合并遵循实际的物理规律。这一特点使得PINN在处理涡流管相关问题时展现出了更高的准确性和可靠性。与传统的普通神经网络模型相比,PINN充分利用了数据集与物理规律之间的内在联系,从而有效避免了模型可能出现的过拟合现象。此外,通过引入物理约束,PINN在建模过程中不仅能够对有限的数据进行准确预测,还具备更强的泛化能力,使其在处理实际工程问题时具有显著的优势。可以说,PINN为复杂流体动力学问题的求解提供了一种更加科学且实用的建模方法。
3结论
本研究通过引入伯努利方程和尼古拉兹公式,成功构建了一种基于物理信息的神经网络(PINN)模型,并将其应用于涡流管数据的预测与分析。该模型以压力 P 、摩擦系数 ζ . 入口温度 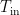 作为人工神经网络的输入值,以冷端温度
作为人工神经网络的输入值,以冷端温度 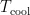 作为输出值,构建了一种能够反映物理规律的神经网络结构,并对模型进行了充分的训练与验证。训练结果表明,所构建的PINN模型的决定系数
作为输出值,构建了一种能够反映物理规律的神经网络结构,并对模型进行了充分的训练与验证。训练结果表明,所构建的PINN模型的决定系数 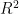 达到
达到 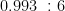 ,均方根误差(RMSE)为0.3392,显示了极高的预测精度和拟合效果。
,均方根误差(RMSE)为0.3392,显示了极高的预测精度和拟合效果。
与传统神经网络模型相比,PINN通过将物理定律直接嵌入神经网络的结构中,实现了数据驱动和物理约束的有机结合。在涡流管这一复杂的非线性热流问题中,PINN不仅显著提升了预测精度,还展现出卓越的泛化能力。尤其是在数据量有限或问题具有强物理约束的情况下,PINN凭借其对物理行为的深度捕捉,成为传统方法难以匹敌的解决方案。
此外,本文对所构建的PINN模型进行了全面的不确定度分析和鲁棒性测试,结果表明该模型在处理不同程度的噪声和不确定性时,依然能够保持高水平的预测准确性和稳定性。这进一步验证了PINN模型在实际工程应用中的可靠性和稳健性,为应对复杂的物理问题提供了强有力的工具支持。
本研究充分证明了物理信息神经网络在复杂物理系统建模中的广阔潜力,为未来的工程应用开辟了新的研究方向。未来,通过进一步优化模型结构、引入更多物理约束以及扩展应用场景,PINN有望在更广泛的工程与科学领域中发挥重要作用,为相关领域的技术创新提供强大助力。
参考文献:
[1]SINGHJ,GILLSS,DOGRAM,etal.Effect ofRanque-Hilsch Vortex Tube Coolingto Enhance the Surface-Topography and Tool-Wear in Sustainable Turning ofAl-5.6Zn-2.5Mg-1.6Cu-0.23Cr-T6 Aerospace Alloy[J/ OL].Materials,2022,15:5681[2024-10-03].https://doi. org/10.3390/ma15165681.
[2]PARKERMJ,STRAATMANAG.ExperimentalStudy on the Impact of Pressure Ratio on Temperature Drop in a RanqueHilsch Vortex Tube [J/OL].Applied Thermal Engineering, 2021,189 (7):116653[2024-10-23].https://doi.0rg/10.1016/ j.applthermaleng.2021.116653.
[3]ATTALLAM,AHMEDH,AHMEDMS,etal.Experimental Investigation of the Effect of Nozzle NumbersonRanque-Hilsch Vortex Tube Performance [J].Experimental HeatTransfer,2017,30(1-3):253-265.
[4]AVCIM.The EffectsofNozzle AspectRatio and NozzleNumber on the Performance of the Ranque-Hilsch Vortex Tube[J].AppliedThermalEngineering,2013,50(1):302-308.
[5] RAFIEE SE,SADEGHIAZAD MM. Experimental Analysis on Impact of Navigators Angle on Velocimetryand Thermal CapabilityofRH-VortexTube[J/OL].AppliedThermal Engineering,2020,169:114907[2024-09-28].https://doi. org/10.1016/j.applthermaleng.2020.114907.
[6]POURARIAH,KIASM,PARKWG,etal.Modeling the Cooling Performance of Vortex Tube Using aGenetic Algorithm-Based ArtificialNeuralNetwork[J].ThermalScience,2016,20(1):53-65.
[7]KAYAH,KIRMACIV,ESHA.Performance ModelingofParallel-ConnectedRanque-HilschVortex Tubes UsingaGeneralizableandRobustANN[J].HeatTransfer,2020, 51(15):1399-1415.
[8]KAYA,HUSEYIN,GULERE,etal.PredictionofTemperatureDepartureofaNitrogen-DrivenVortex TubewithLinear,Knn,SVM,and RFRegressionModels[J].NeuralComputing and Applications,2022,35:6281-6291.
[9]LIHW,HAOS,NIYQ,etal.HybridStructuralAnalysisIntegratingPhysicalModelandContinuous-Time State-SpaceNeural NetworkModel[J].Computer-aided civil andinfrastructure engineering,2025,40(2):166-180.
[10]ZHENGXW,ZHOUS,LVH,etal.Hybrid Physics-BPNeuralNetwork-BasedStrengthDegradationModel of Corroded Reinforcements Under the Simulated Colliery Environment[J].Structures,2023,50:524-537.
[11]XIAOMJ,YUTC,ZHANGYS,etal.PhysicsInformedNeuralNetworksforthe Reynolds-Averaged NavierStokesModeling ofRayleigh-Taylor Turbulent Mixing[J/OL]. Computersamp; Fluids,2023,266:106025[2024-09-17].https:// doi.org/10.1016/j.compfluid.2023.106025.
[12]WENT,CHENC,ZHENGG,etal.UsingaNeural Network-Physics-BasedHybridModeltoPredictSoilReaction Fronts[J/OL].Computersamp;Geosciences,2022,167(C) [2024-09-26].https://doi.org/10.1016/j.cageo.2022.105200.
作者简介:李申申(1997一),男,汉族,河南周口人,硕士在读,研究方向:智能检测与控制。