
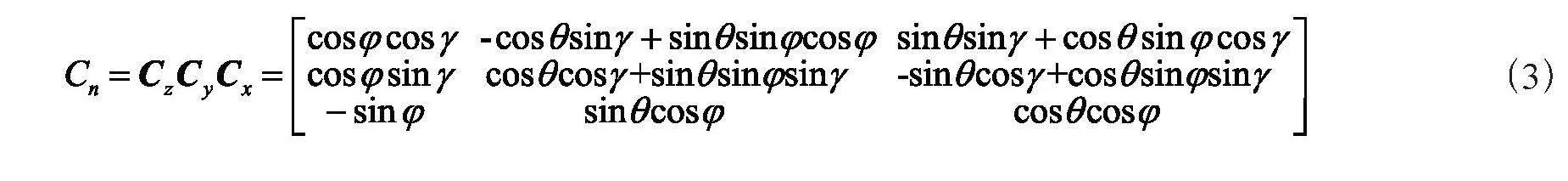

摘 要:传统单点的地磁匹配定位算法运算量大,且定位时效性及定位精度较差。针对该问题,采用基于序列的快速动态时间规整算法Fast-DTW实现多维的地磁序列匹配,并利用最长公共子序列LCS的有序聚类进行优化。离线阶段通过坐标转换法构建四维地磁指纹库,在线阶段进行实时地磁序列匹配,获得定位结果。实验结果表明,该算法的定位时效性及精度均有提升。
关键词:地磁室内定位;快速动态时间规整算法;最长公共子序列;地磁指纹库
中图分类号:TN966;P318 文献标识码:A 文章编号:2096-4706(2024)08-0089-05
0 引 言
基于全球定位系统的室外定位技术已诞生多年,经历不断革新几乎已达到可以满足人们在室外日常出行的最大需求。但对于室内定位方面,该技术还存在一定的局限性,卫星信号在传递过程中被建筑物内墙体以及一些室内设备等层层削弱,传递至室内时信号已十分微弱,无法继续满足正常的定位需要,实现室内精确定位仍需选择其他信号源进行参与[1]。目前研究较为深入的室内定位信号源,包括蓝牙、Wi-Fi、超宽带、射频识别等,均需要一定的基础设备在室内进行部署,且均需要一定的更新以及维护保证其稳定运行[2]。利用室内地磁信息实现定位无须考虑这些成本,室内地磁信号无处不在,且由于建筑物的影响,室内不同位置的地磁信号的分布也各有差异;同时地磁信号在稳定抗干扰、室内外无缝定位以及多源融合定位方面也有一定的可研究性[3]。
目前基于地磁信息的室内定位主要是通过指纹定位的方式实现,指纹定位方式又分为两种,分别是基于序列的磁匹配定位(Sequence-Based Magnetic Matching Positioning, SBMP)以及基于单点的磁匹配定位(Single Point-Based Magnetic Matching Positioning, SPMP)[4],对此国内外许多学者均有研究。基于序列的磁匹配定位技术以动态时间规整算法为主要应用,Chen等人[5]采用非磁航向和磁航向组合,将惯性递归信息集成到地磁DTW中,并对准静态和非准静态范围进行划分,提高匹配成功率和位置修正可靠性。Zhao等人提利用智能手机和众包技术收集磁轨迹数据构建室内地图,通过DTW聚类和亲和传播算法轨迹融合实现精准定位。金俊超等人[6]使用UCR策略对DTW算法进行改进,通过序列重排序及约束策略提高计算效率的同时提升定位精度。
单点的磁匹配定位技术相较于序列匹配,面临分辨率更低、工作量更大且对匹配算法的性能要求更高的情况,往往需要以大量的数据集训练实现精确定位,因此该技术通常以机器学习方法为主要应用,如BP神经网络、贝叶斯、加权K近邻算法等[7-9]。本文基于DTW算法实现基于序列的磁匹配室内定位,针对传统DTW算法定位效率及定位精度较差的缺陷,采用最长公共子序列(Longest Common Subsequence, LCS)的有序聚类进行优化,构建基于LCS-Fast-DTW地磁序列匹配模型,并通过实验验证该模型的定位性能。
1 多维指纹库构建
地磁室内定位中,指纹定位的核心部分为离线阶段及在线阶段,如图1所示。离线阶段为地磁数据的采集、存储,在实验区域内采集完整的位置信息以及对应的地磁信息,建立位置信息与地磁信息一一对应的数据库即指纹库;在线阶段,通过智能手机在实验路径中获取在线采集实时的地磁数据,利用匹配算法与指纹库中的整体数据进行匹配,以此获得最为接近的位置估计。由于室内地磁场的分辨率较低,指纹库中会存在较多不同空间位置对应相似地磁序列的情况,容易引起位置估计混淆,产生较大定位误差[10]。因此,指纹库的分辨率、匹配算法的性能都是实现精确地磁定位的关键因素。
在进行地磁数据的采集时,同一时间同一位置采集的地磁信息并不是唯一不变的,不仅仅受设备的硬件噪声的干扰,最主要的原因是受采集设备本身姿态的限制。通过采集设备获取的地磁X轴、Y轴、Z轴的数据是基于设备本身坐标系下的数据,该数据会随着设备姿势的变化而不断变化,实际需要应用于室内定位的地磁数据是基于地理坐标系下的稳定的数据。因此通常有两种方式来解决上述问题:
1)多数学者通过计算地磁模值的方式消除设备姿态的影响,计算式为:
(1)
其中,Mx、My、Mz分别表示智能手机采集的三轴数据。
2)还可通过坐标转换的方法解决,即将采集的设备自身坐标系下的地磁三轴数据与旋转矩阵相乘,即可获得稳定的地理坐标系下的三轴数据,可令 、、 分别表示转换后的地理三轴数据。采集过程中手机姿态变化角度分别为俯仰角(φ)、航向角(γ)及横滚角(θ)。该角度可直接由智能手机内部的传感器获取。其转换算式为:
(2)
其中,Cx、Cy、Cz分别表示俯仰角、航向角、横滚角对应的旋转矩阵。为进一步提升指纹库的分辨率以及稳定性,本文将位置信息与其对应的坐标转换后的地磁三轴数据、地磁模值一起输入构建四维的地磁指纹库。
2 LCS-Fast-DTW定位算法构建
2.1 LCS算法
最长公共子序列(Longest Common Subsequence, LCS)通常被用来衡量数据之间的相似度,同时对于非线性序列在降噪及排列扭曲方面有较好的效果。使用智能手机在行走过程中采集地磁数据时,相同时间点采集的磁序列长度存在差异,且因设备以及外界因素,采集的数据不可避免地存在噪声干扰,因此在进行序列匹配时可预先利用LCS算法找到最长的地磁数据子序列,抵消噪声的影响,进一步提升算法的定位性能,LCS的具体计算原理如下。
假定存在二维数组D中存在序列X及序列Y,其中D[i]表示X序列中的前i个元素;D[ j]表示Y序列中的前j个元素,在此基础上设定阈值σ,对于数组D的任意元素,可存在:
1)若X [i]与Y [ j]之间的距离小于预设的阈值,则D[i] [ j] = D[i-1] [ j-1] + 1,即在原有的最长公共子序列长度加1可得当前最长公共子序列长度。
2)若X [i]与Y [ j]之间的距离大于预设的阈值,则D[i] [ j] = max (D[i] [ j-1],D[i-1] [ j]),即在原有及当前的最长公共序列中选取长度较大的那个。以此类推,直到可以计算出D的所有元素,最后C [n] [m]就是序列X和Y的最长公共子序列的长度。相似度S的计算式为:
(4)
其中, LCS 为找到的最长公共子序列长度, X 表示序列X的最长公共子序列的长度, Y 表示序列Y的最长公共子序列的长度。
2.2 Fast-DTW算法
动态时间规整算法(Dynamic Time Warping, DTW)是一种根据序列之间的相似度进行匹配的算法,该算法可将两个信号序列看作是在时间轴上分布的点序列,通过“扭曲”这两个信号序列中的时间轴,可在所处不同时间间隔内的信号之间找到其对应关系,因此被广泛应用于语音识别、时间序列匹配和相似性搜索等领域。在地磁室内定位中,需要利用DTW算法对实时采集的地磁序列与离线阶段行人行走所构建的地磁指纹库中的序列组进行匹配。所构建的指纹库实际为一组较长的地磁序列,DTW的核心思想是创建一个代价矩阵,其中该矩阵的每个元素代表两个地磁序列在某一点上的差异。该元素可用欧氏距离来表示,计算式为:
(5)
其中,m表示实时采集的地磁序列,Ml表示构建的地磁指纹库中第l个磁序列,d表示上述两个序列之间的二维欧氏距离。随后采用全局搜索的方式搜索通过代价矩阵的最短距离,同时设定一个滑动窗口,路径的搜索空间被限制在该窗口,最终,计算出该路径的所有点的代价之和,即累计距离之和,当这个距离总和最小时,即可确定两个序列之间最佳匹配关系。
传统DTW计算的时间以及空间的复杂度为N2,N为序列的长度,当定位面积较大时,相应的地磁序列的长度也较长,因此传统DTW计算工作量巨大且效率随之降低。因此在此基础上,本文引入基于序列的快速动态时间规整算法(Fast Dynamic Time Warping, Fast-DTW)以降低计算的复杂程度。
Fast-DTW实际为DTW的近似解法,DTW算法通常直接对原始的序列进行处理及运算,Fast-DTW首先对原始序列下采样处理,可设置下采样率为k,因此每隔k个时间点取一个点,即可获得新的较短的时间序列,在该较短的序列上运用传统DTW算法,获得初步序列粗略的对齐关系。随后运用插值处理,将初步的DTW矩阵扩大到原始时间序列的长度,获得在原始序列长度上粗略的对应关系。最后,在此基础上对原始数据进行微调,以此获得最终的最佳匹配关系。该方法可将计算的时间以及空间的复杂度降低为N,大大减少计算的复杂度。
2.3 LCS-Fast-DTW定位算法
由于地磁场的分辨率较低,在指纹库序列足够长时,会不可避免出现较多序列相似的情况;同时由于行走过程中的步频不能保证统一,会出现部分数据丢失或产生额外数据情况的发生。因此Fast-DTW算法虽然可一定程度上降低计算复杂程度,但仍不能保证序列匹配的正确率,因此,本文利用最长公共子序列的有序聚类对齐其进行优化,LCS算法的复杂性较低且可以更加精确的衡量地磁序列之间的相似性,具体优化过程为:
1)数据预处理,对采集的地磁数据划分整体样本集以及测试集。
2)首先对所有测试集的地磁序列进行LCS相似度计算,获得相应的相似度结果。
3)根据得到的LCSS相似度矩阵,使用K-means聚类算法来划分参考指纹库,获得相似度最大的聚类标签和各个聚类的中心点。
4)在获得的聚类结果中运用Fast-DTW算法进行计算,选择距离最小的参考序列,其对应的位置可认为是最接近测试序列的实际位置。
3 实验与结论
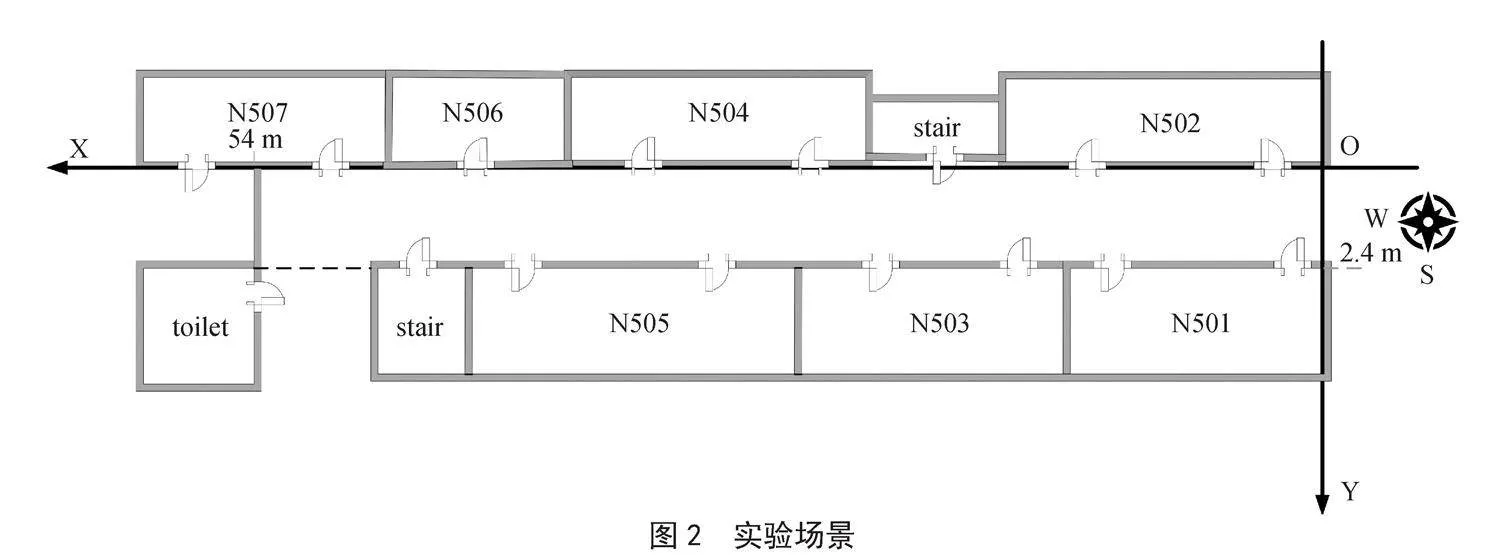
试验场地设在安徽理工大学空间信息与测绘工程学院的五楼走廊,该走廊长为54 m,宽为2.4 m,走廊较为空旷且无大型电磁设备等干扰,试验场地具体情况如图2所示。将整个实验区域用1.2 m×1.2 m的网格均匀划分,并通过往返匀速行走的方式在每个网格节点处采集地磁数据,直至将实验区域内所有位置的数据采集完毕。本文使用的采集设备为iPhone12,采集软件为开源的物理采集软件,可采集加速度数据、陀螺仪数据、地磁三轴数据等,采集频率为50 Hz,每个点位采集15 s,采集过程中尽可能保证设备姿势不变。离线阶段数据采集完成后,规划实验路径,在线阶段在路径中匀速行走并采集在线地磁数据,用于后续的磁序列匹配。
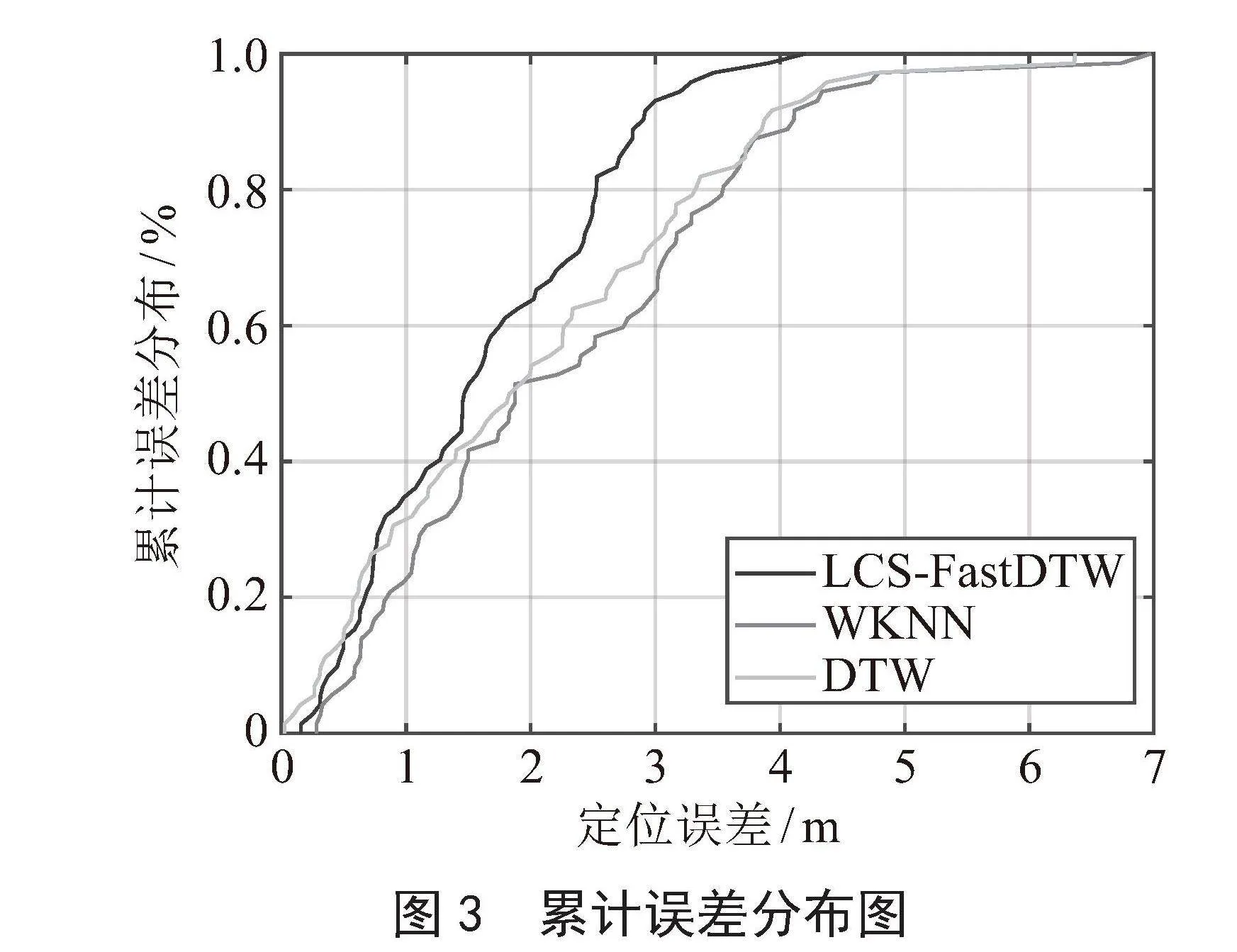
本文的实验路径从起点向西一直匀速行走至走廊终点处,行走距离为54 m。为使指纹库的数据序列更为完整,采用克里金插值方式处理离线指纹库。为减小采集设备的硬件磁性误差以及设备姿势轻微晃动的影响,采用低通滤波对数据进行预处理。将在线阶段采集的数据作为测试集输入至构建的LCS-Fast-DTW序列匹配模型中,并采用五折交叉验证法验证该模型的定位性能,并将相同的测试点位分别输入至DTW算法、WKNN算法进行对比,进一步验证本文模型的定位性能,实验结果如图3所示。
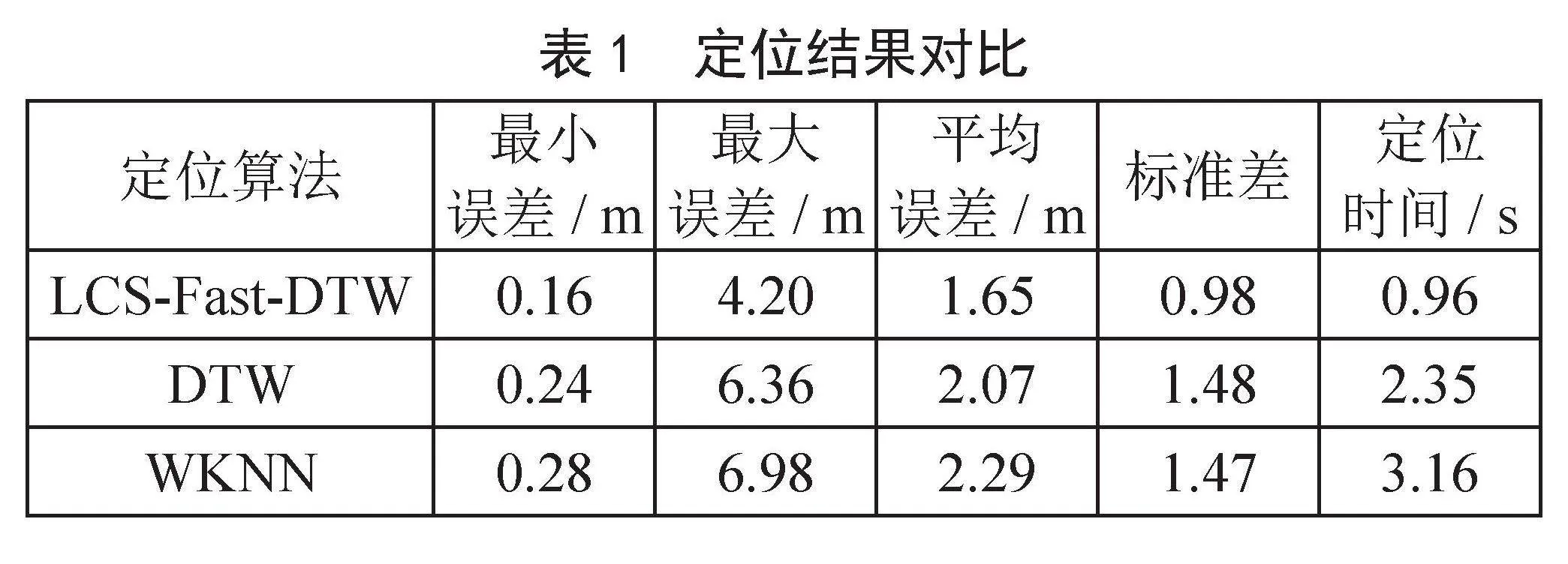
由图3可知,LCS-Fast-DTW算法的定位误差集中在2.5 m以内,占比为77.8%,DTW算法的定位误差集中在3 m以内,占比为72.2%,WKNN算法的定位误差集中在3.5 m以内,占比为79.1%,这三种算法在误差1 m以内的占比分别为36.1%、31.9%及23.6%。因此,本文算法具有较高的定位精度。三种算法的不同定位指标如表1所示。
由表1可知,本文算法的平均定位误差、定位标准差以及定位时间均低于其他两种算法,在保证定位精度的同时兼具定位稳定性及定位时效性,具有最佳定位性能,可有效应用于地磁室内定位。
4 结 论
本文以地磁室内定位为主要研究内容,在传统地磁模值的基础上利用坐标转换方法构建四维的地磁指纹库,基于DTW算法进行磁序列匹配实现定位,并利用最长公共子序列的有序聚类对其进行优化。实验结果表明,本文构建的LCS-Fast-DTW算法具有较好的定位性能,可有效应用于室内定位,同时,该定位方式可为地磁与其他定位信号源进一步结合实现多源融合定位提供研究基础,也可为井下、隧道等特殊场景定位提供一定的参考。
参考文献:
[1] GEOK T K,AUNG K Z,AUNG M S,et al. Review of Indoor Positioning: Radio Wave Technology [J/OL].Applied Sciences,2021,11(1):279(2020-12-30)[2023-08-08].https://doi.org/10.3390/app11010279.
[2] PASCACIO P,CASTELEYN S,TORRES-SOSPEDRA J,et al. Collaborative Indoor Positioning Systems: A Systematic Review [J/OL].Sensors,2021,21(3):1002.(2021-02-02)[2023-08-08].https://doi.org/10.3390/s21031002.
[3] SONG S S,FENG F,XU J S. Review of Geomagnetic Indoor Positioning [C]//2020 IEEE 4th International Conference on Frontiers of Sensors Technologies (ICFST).Shanghai:IEEE,2020:30-33.
[4] SUN M,WANG Y J,XU S L,et al. Indoor Geomagnetic Positioning Using the Enhanced Genetic Algorithm-Based Extreme Learning Machine [J].IEEE Transactions on Instrumentation and Measurement,2021,70:1-11.
[5] CHEN J W,ZHANG W C,WEI D Y,et al. Research on Indoor Constraint Location Method of Mobile Phone Aided by Magnetic Features [C]//2022 IEEE 12th International Conference on Indoor Positioning and Indoor Navigation (IPIN).Beijing:IEEE,2022:1-7.
[6] 金俊超,马昌忠,陈国良,等.基于UCR-DTW的地磁序列定位算法 [J].合肥工业大学学报:自然科学版,2021,44(11):1551-1556.
[7] 韩雨辰,余学祥,仲臣,等.融合光照强度的地磁室内定位方法研究 [J].测绘科学,2022,47(7):35-42.
[8] 王安义,欧雪.基于粒子滤波的PDR/地磁指纹室内定位 [J].测绘通报,2021(1):24-28.
[9] 马跃欣,冯秀芳.基于有序聚类和MSKPCA的室内定位算法 [J].计算机工程与设计,2021,42(4):963-968.
[10] 孙猛,汪云甲,周家鹏,等.一种基于快速动态时间规整的地磁定位算法 [J].测绘科学,2020,45(8):77-82.
作者简介:姚霆宇(1998—),男,回族,安徽安庆人,硕士在读,研究方向:室内定位方向。
收稿日期:2023-09-08
基金项目:安徽省重点研究与开发计划(202104a07020014);安徽省科技重大专项(202103a05020026)
DOI:10.19850/j.cnki.2096-4706.2024.08.020
Research on Multidimensional Geomagnetic Sequence Matching Algorithm
Based on Improved Fast-DTW
YAO Tingyu1,2,3, YU Xuexiang1,2,3, HAN Yuchen1,2,3, ZHU Ping1,2,3
(1.School of Spatial Information and Surveying Engineering, Anhui University of Science and Technology, Huainan 232001, China;
2.Key Laboratory of Aviation-aerospace-ground Cooperative Monitoring and Early Warning of Coal Mining-induced Disasters of Anhui Higher Education Institutes, Anhui University of Science and Technology, Huainan 232001, China;
3.Coal Industry Engineering Research Center of Mining Area Environmental and Disaster Cooperative Monitoring, Anhui University of Science and Technology, Huainan 232001, China)
Abstract: The traditional geomagnetic matching positioning algorithms based on single points have a large computational overhead and relatively poor positioning timeliness and accuracy. To address this issue, this paper uses the Fast Dynamic Time Warping (Fast-DTW) algorithm based on sequences to implement multi-dimensional geomagnetic sequence matching, and optimizes it using ordered clustering of the Longest Common Subsequence (LCS). During the offline phase, a four-dimensional geomagnetic fingerprint database is constructed by coordinate transformation methods. In the online phase, real-time geomagnetic sequence is matched to obtain positioning results. The experimental results show that the positioning timeliness and accuracy of the algorithm have been improved.
Keywords: geomagnetic indoor positioning; Fast-DTW; LCS; geomagnetic fingerprint database