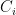



摘 要:文章对基于压缩感知的无线传感器网络定位算法进行了研究,存在重构算法计算量大、定位误差较大等问题,为降低计算复杂度和定位误差,文章提出基于贝叶斯分层模型的低复杂度无线传感器网络定位算法。首先,将稀疏贝叶斯分层先验模型引入到无线传感器网络的定位中;其次,通过运用稀疏贝叶斯理论推理出估计目标的后验概率分布;最后,结合变分消息传递(VMP)算法,使用辅助函数对未知变量的联合后验概率密度函数进行等效,得到目标位置向量的估计结果。仿真结果表明,相较于传统的重构算法,文章提出的方法具有更好的恢复效果,计算复杂度更低。
关键词:压缩感知;贝叶斯分层模型;低复杂度;重构算法
中图分类号:TN929.5;TP212.9;TP312 文献标识码:A 文章编号:2096-4706(2024)08-0106-05
DOI:10.19850/j.cnki.2096-4706.2024.08.024
0 引 言
位置服务信息广泛应用在军事、医疗、交通等一些领域[1]。无线传感器网络(Wirelesssensor network, WSN)在安防监控、入侵检测、目标跟踪、环境监测、医疗护理和物联网等领域的应用越来越深入[2]。在WSN中,实现精准的定位是一项至关重要的任务。
近年来,压缩感知(Compressive sensing, CS)技术的引入为WSN的位置定位提供了全新的思路[3]。对于WSN中基于压缩感知的定位算法,其最关键的就是位置向量重构算法的设计。文献[4]为解决目标与初始网格点偏差导致的基不匹配,建立了拉普拉斯(Laplace)先验的稀疏贝叶斯学习框架。文献[5]在单采样下以压缩感知的方法研究三维环境中无线传感器网络技术,证明了正交匹配追踪算法与贝叶斯压缩感知理论应用在三维环境的可行性,但未考虑到三维环境的复杂性与算法的复杂度。文献[6]将基于变分贝叶斯推理的重构算法和K-均值聚类算法结合进行多目标定位。此外在贝叶斯方法的基础上还引入了分层模型,文献[7]提出了一种具有自适应拉普拉斯先验的分层贝叶斯框架来避免高维矩阵的逆运算。
基于压缩感知技术的WSN定位研究还存在着一定的不足:1)选取的先验模型无法与后验概率共轭,导致计算复杂。2)在计算复杂度与重构精度间难以取得有效平衡。3)忽略了环境的复杂性,特别是在低和中信噪比的情况下。
鉴于上述问题,本文提出的基于贝叶斯分层模型的低复杂度无线传感器网络定位算法,使其能够在低和中等信噪比的情况下也可以得到比较好的定位效果。
1 定位模型和问题描述
1.1 定位模型
本文采用如图1所示的基本场景。假设传感器节点与目标节点均为静止状态,M个位置已知的传感器节点被随机布置于无线传感器监控器区域内,同时K个目标也被随机分布在待监测区域内。假设所有节点都具有相同的感知半径R,每个信标节点都在目标节点的信号传播范围内。为了稀疏表示目标的位置,将待监测区域网格化,定义区域为正方形,并将其均匀地分成N个网格,且每个网格内均至多包含一个目标,假设目标位置即为网格的中心位置,传感器位置则为先验信息。
1.2 问题定义
压缩模型可定义为:若N×1维的信号S在N×N维的稀疏基Ψ上,用K稀疏度的信号S来表示,在另一个与稀疏基不相关的M×N维观测矩阵Φ上进行投影,其中M ≪ N,可得到M×1维的压缩采样矩阵y,在此过程中受到观测噪声n的影响。其模型公式为:
(1)
式中,已知测量值y与观测矩阵Φ,需求得N×1维的稀疏信号S,即为压缩感知过程。因此定位问题转化成了根据传感器位置生成的观测矩阵和实时测量值重构N×1维的稀疏信号S的问题(即重构下述的目标位置向量)。
下面将式(1)中的参数记为:
1)目标构成的稀疏矩阵S。目标的位置信息可用N×1维的稀疏向量表示,即:
(2)
式(2)中: 为目标位置向量,其元素Sn ∈ {0,1}。当网格n内存在目标时,Sn = 1;否则Sn = 0。由于K ≪ N,因此S为K稀疏向量。
2)构造稀疏基矩阵Ψ。由于稀疏信号S本身稀疏,为方便设计,稀疏基Ψ为N×N维的单位矩阵。
3)观测矩阵Φ。独立同分布的高斯随机测量矩阵可转换为普适的压缩感知测量矩阵,可以用来模拟多径衰落信道对信号的影响,以确保仿真结果的准确性。
4)测量值矩阵y。定义y = {y1,y2,…,yM}T为测量值矩阵,则:
5)感知矩阵Θ。感知矩阵Θ构建了测量值矩阵y与目标位置向量S之间的关系。
2 稀疏贝叶斯分层先验模型
2.1 分层先验模型的建立
本文通过对先验信息建立分层的架构,利用高斯尺度混合(GSM)来描述稀疏性诱导先验。
首先将数学模型(1)中的联合概率密度函数分解为因子,并将其表示为分层先验模型:
(3)
针对诱导稀疏性问题,构建了如图2所示三层高斯尺度混合式先验模型。圆形节点所代表的是随机变量,方形节点代表着确定性参数,而箭头则呈现了各节点之间的从属关系。y为测量值,其值取决于随机变量S和n。S是目标位置向量,是需要恢复的稀疏向量,其值取决于随机变量γ,而γ又取决于随机变量ε和η。n为测量噪声向量,其值取决于随机变量λ。因为测量噪声向量n是加性高斯随机白噪声,其方差矩阵为λ-1I,λ>0为噪声精准系数,所以n服从复高斯分布,似然分布可表示为:
(4)
式(4)中:λ-1表示测量噪声的方差。由于测量噪声向量服从多维复高斯分布且共轭先验是伽马分布。所以,把λ看作随机变量,假设它服从伽马先验分布:
(5)
式(5)中:该先验分布的确定性参数包括c和d。先验模型的第一层中,把S看作随机变量,假设它服从复高斯分布:
(6)
式(6)中: 表示S的方差。先验模型的第二层中,把γ看作随机变量,假设它服从伽马先验分布:
(7)
式(7)中:随机向量η的元素ηl之间相互独立,其中元素γl满足伽马分布为率参数(rate parameter)。 表示伽马函数。先验模型的第三层中,把η看作随机变量,其元素ηl也满足伽马分布:
(8)
式(8)中:al和bl是确定性参数,它们分别表示伽马分布的形参数(shape parameter)和率参数。根据构建的三层高斯尺度混合先验模型,将S的先验分布表示为:
(9)
(10)
式(9)和(10)中:S服从Bessel K分布,ε表示Bessel K分布中的形状参数,与稀疏性有关,越小表示稀疏性越强。η表示Bessel K分布中的尺度参数,参数ρ表示实复数信号。Kε-ρ是第二类修正Bessel函数,ε-ρ为第二类修正Bessel函数的阶数。更多关于先验模型的推导参见文献[8]。
2.2 目标位置估计
为了更好的估计出目标位置向量S,在上述分层模型的基础上,利用变分消息传递(VMP)算法,通过分块来降低复杂度。下面2.2.1小节具体展开描述。
2.2.1 后验概率分布估计
在三层高斯尺度混合先验模型中,对式(3)的联合概率密度函数进行进一步的分解为:
(11)
由式(4)可知每一个测量值yd,d = 1,…,D是相互独立的且满足复高斯分布。根据式(11),采用文献[9]的因子图模型,图3是消息传递的因子图。
图3中:fλ = p (λ),fyd = p ( yd s,λ),fsl = p (sl γl),fyl = p (γl ηl),fηl = p (ηl)。
令Z = {S,γ,η,λ}作为隐藏的未知参数的集合,H = {a,b,c,d,ε}作为确定性参数的集合。要恢复目标位置向量S,就需要求出Z的后验概率分布。在该算法的初次迭代中,要更新目标位置向量S的后验分布,计算均值μ与协方差 ,然后在后续迭代中更新各个参数。
由于无法求出各个未知参数的具体表达式,所以选择改进的变分消息传递(VMP)算法来近似最大后验估计。令Q (Z)为辅助函数,通过计算函数节点到变量的消息与变量到函数节点的消息这二者之间消息的乘积来更新辅助函数,其计算公式为:
(12)
初次迭代中,在假设式(9)和式(10)先验的情况下,给定字典Θ和测量值矩阵y,根据稀疏贝叶斯推理,目标位置向量S的后验服从均值为μ,方差为" 的复高斯分布,其计算公式为:
(13)
(14)
式(14)中,,需要对L×
L维的矩阵求逆,复杂度为O(L3)。当L很大时,其计算量很大,因此对式(14)进行分块降低复杂度,由此在后续更新中,辅助函数Q(Z)变为:
(15)
其中Q(γ),Q(η)和Q(λ)的更新规则分别如下:
(16)
(17)
(18)
式(15)中的Q(Sq)对目标位置向量S分解成q块,每块大小为B,由此可知q = L / B。基于上述改变,将式(13)和(14)改写为:
(19)
(20)
此时式(20)为对B×B维的矩阵求逆,复杂度为O (B3),因为B<L,所以维度降低减小计算复杂度。经过迭代,算法收敛后,需要重组" 和" 的数据,在此定义重组后的" 为μlast,重组后的" 为 ,均值μlast即为目标位置向量的估计值。
2.2.2 算法流程
基于上述后验分布估计可以恢复目标位置向量。表1所示为目标位置的估计算法。将均方根误差(Root Mean Square Error, RMSE)作为衡量定位误差的度量值。均方根误差距离定义为待估计的目标位置向量" 和原始的真实位置向量S之间的误差。当RMSE越小,说明估计的位置就越准确。公式为:
(21)
式(21)中: 表示第c次蒙特卡洛实验中第k个目标的位置向量,K表示需要估计的目标数目,C表示蒙特卡洛实验次数。
算法步骤如下:
输入:测量值矩阵y,观测矩阵Φ,迭代次数tmax
输出:目标位置向量 ,均方根误差RMSE
1.初始化参数a = 1,b = 10-6,ε = 0,ρ = 1,c = d = 0,tmax = 1 000
2.第一次迭代计算S估计值
3.根据式(13)和式(14),计算μ和
4.后续迭代
5.while(t≤tmax)do
6.根据式(16),式(17)和式(18),更新参数γq,ηq,λq
7.根据式(19)和式(20),更新" 和
8.重组分块后的" 和 ,结果分别为μlast和
9.令
10. end while
11.令恢复的位置向量 = μlast,目标个数K = ,RMSE。
3 实验设置及结果分析
3.1 环境及参数设置
通过MATLAB R2021a仿真验证了本文定位算法的有效性,所述定位区域设置为256 m×256 m的方形区域,均匀划分成N个大小相同的网格,在网格中随机配置了M个传感器,在待监测区域随机分布了K个目标。在假设观测值受到零均值高斯白噪声干扰的情况下,用SNR来描述信噪比。所有仿真进行蒙特卡洛实验100次。
3.2 结果及分析
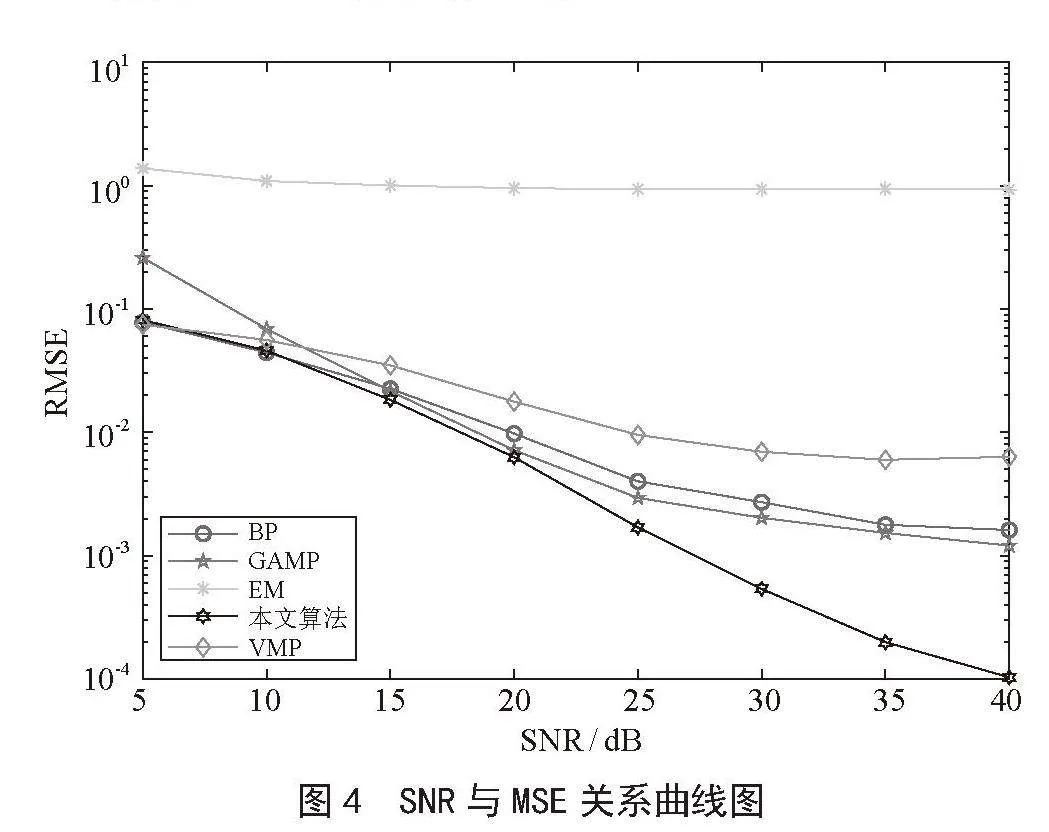
图4表明不同信噪比下稀疏重构算法的定位性能。为了验证算法的性能,分析算法在不同信噪比条件下的RMSE,将本文算法与传统重构算法BP算法,GAMP算法,EM算法以及VMP算法进行对比。其中,M = 10,N = 256 256,K = 5,迭代次数t为20次,蒙特卡洛实验次数C为100次。由图可知,随着噪声逐渐减小,五种算法的RMSE逐渐减小,说明估计的位置越准确。随着信噪比的继续增加,信噪比SNR>25 dB时各种算法的性能提升较小,此时噪声不再是影响定位精度的主要原因了。
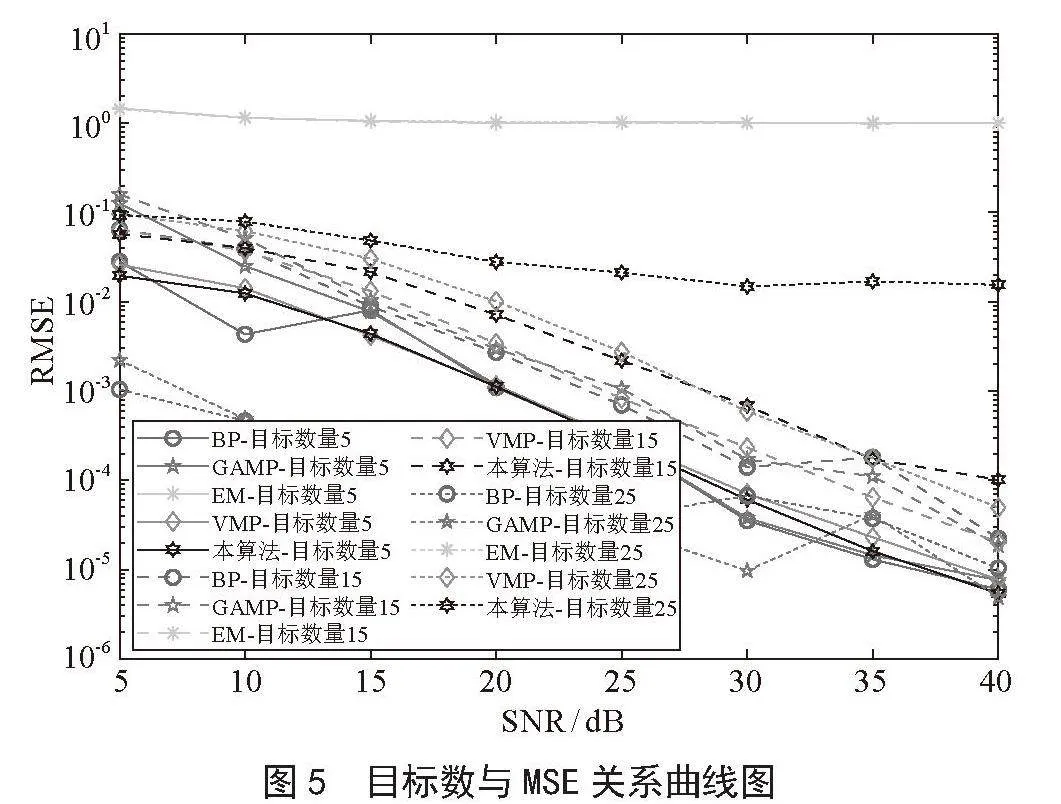
图5表明不同目标数下稀疏重构算法的定位性能。在该仿真实验中,信噪比SNR = 10 dB,迭代次数为20次,总体来看,EM算法的效果最差,本文算法相较于BP算法和VMP算法,其RMSE略大,但是比较稳定,保持在一定范围内波动,是因为在降低复杂度的同时牺牲了部分性能。
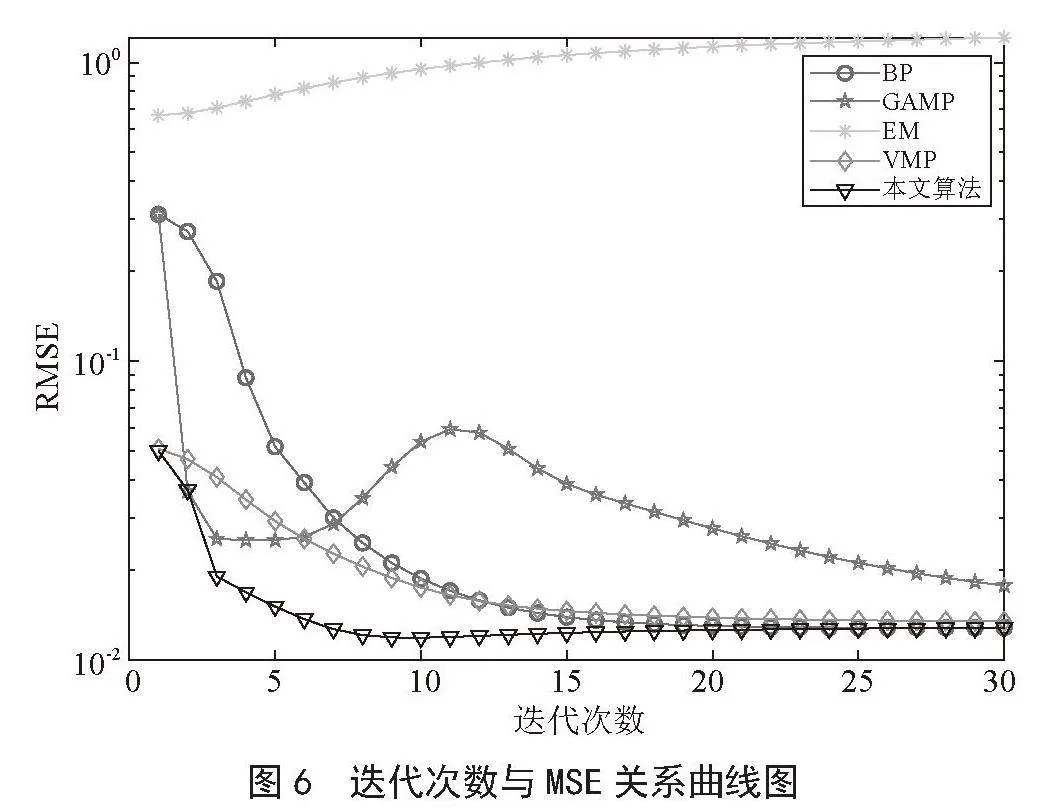
图6表明目标位置向量估计误差和稀疏重构算法中的迭代次数紧密相关。在该仿真实验中,目标数K = 5,信噪比SNR = 10 dB。由图可知,随着迭代次数的增加,五种算法的RMSE基本呈下降趋势总体来看,本文算法的性能最好,当迭代到20次时,除了EM算法无法达到收敛,其余算法都将趋于收敛,此时迭代次数不再是影响定位性能的主要因素了。
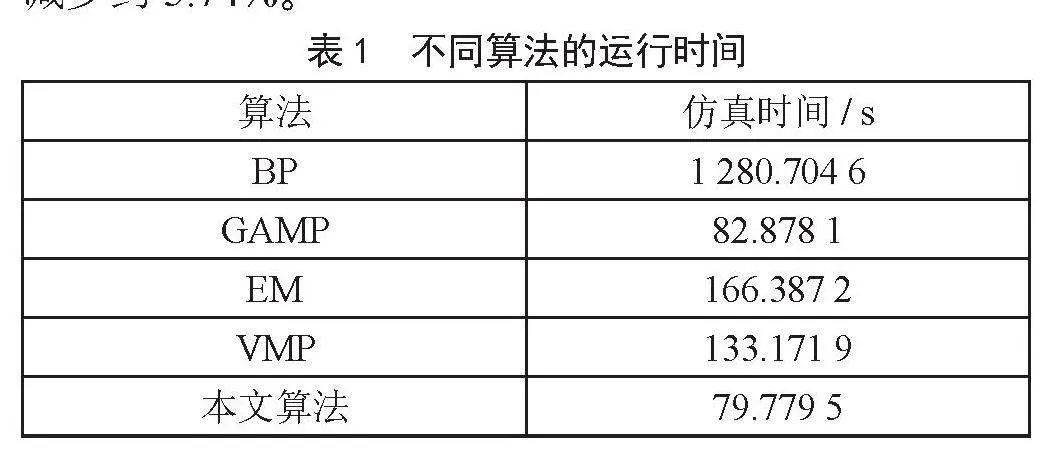
为了寻求算法计算复杂度与定位误差之间的平衡。表1给出了不同算法的仿真时间,本实验在处理器为Intel Core i5-8250,主频为1.80 GHz,内存为8 GB,软件环境为Windows 10下运行的结果。在仿真时间上,本文算法较原始VMP算法的仿真时间缩短约40.09%,比BP算法减少约93.77%,比GAMP算法减少约3.74%。
4 结 论
本文提出的基于贝叶斯分层模型的低复杂度无线传感器网络定位算法,在低和中等信噪比下,不同迭代次数下,具有较强的抗噪性和鲁棒性。而在不同目标数下,将定位性能与复杂度两者进行了折中,在计算复杂度上进行了有效降低。
参考文献:
[1] 杨彩云,顾锦,夏志东,等.基于轨迹预测的双锚节点移动定位方法研究 [J].传感技术学报,2021,34(9):1250-1257.
[2] 盛金锋,李宁,郭艳,等.基于相位偏移的压缩感知无源多目标定位方法 [J].中国科学院大学学报,2024,41(2):241-248.
[3] 张小康.基于压缩感知的无线传感器网络定位研究 [D].合肥:合肥工业大学,2022.
[4] 游康勇,杨立山,刘玥良,等.基于稀疏贝叶斯学习的网格自适应多源定位 [J].电子与信息学报,2018,40(9):2150-2157.
[5] 李颂.单采样下基于压缩感知的无线传感器网络节点三维定位方法研究 [D].长春:吉林大学,2019.
[6] 陈承,李宁,郭艳,等.结合K-均值聚类的无源目标定位技术 [J].通信技术,2022,55(7):871-880.
[7] WANG D,WANG T,CUI W. A fast sparse Bayesian learning method with adaptive Laplace prior for space‐time adaptive processing [J].IET Radar,Sonar amp; Navigation,2022,16(12):1936-1948.
[8] PEDERSEN N L,MANCHÓN C N,BADIU M A,et al. Sparse estimation using Bayesian hierarchical prior modeling for real and complex linear models [J].Signal processing,2015,115:94-109.
[9] KANG H,LI J,GUO Q,et al. Pattern coupled sparse Bayesian learning based on UTAMP for robust high resolution ISAR imaging [J].IEEE Sensors Journal,2020,20(22):13734-13742.
作者简介:翟永祺(1996--),女,汉族,山西太原人,硕士研究生在读,研究方向:无线传感器网络。
收稿日期:2023-10-10
Low-complexity Wireless Sensor Network Location Algorithm Based on
Bayesian Hierarchical Model
ZHAI Yongqi
(School of Computer Science and Mathematics, Fujian University of Technology, Fuzhou 350118, China)
Abstract: In this paper, the algorithm of wireless sensor network location based on compression perception is studied, and there are some problems such as large computation of reconstruction algorithm and large positioning error. In order to reduce the computational complexity and localization error, a low complexity wireless sensor network localization algorithm based on Bayesian Hierarchical Model is proposed. Firstly, the sparse Bayesian hierarchical priori model is introduced into the positioning of wireless sensor networks. Secondly, by using sparse Bayesian theory, the transcendental probability distribution of estimated target is deduced. Finally, combined with Variational Message Passing (VMP) algorithm, the joint posterior probability density function of unknown variables is equivalent by auxiliary function, and the target location vector is estimated. The simulation results show that the proposed method in this paper has better recovery effect and lower computational complexity than traditional reconstruction algorithm.
Keywords: compressive sensing; Bayesian Hierarchical Model; low complexity; reconfiguration algorithm