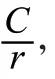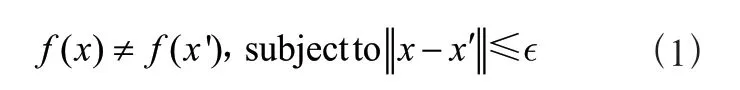
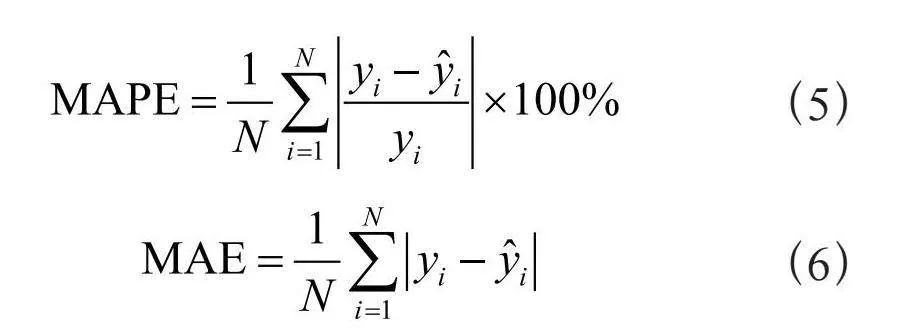

摘" 要:由于天气对农业生产、水资源管理和自然灾害预防等具有重要影响,文章采用ARIMA模型来实现对天气的有效预测。通过利用ACF和PACF图粗略确定ARIMA模型的参数,最终确定最优模型:ARIMA(1,1,1)为日最低气温模型,其残差序列自相关函数与偏自相关函数基本落在95%置信区间内;同时Ljung-Box Q统计结果表明残差不存在相关关系(P>0.05),即残差为白噪声,满足随机性假设;最终计算误差(日最低气温)RMSE、MAPE、MAE分别为2.63、1.22%、2.06,预测结果良好,为定西天气的预测提供了可行的方案。
关键词:天气预测;时间序列插值法;ARIMA模型
中图分类号:TP391.1" 文献标识码:A" 文章编号:2096-4706(2024)09-0140-04
Analysis and Prediction of Dingxi Weather Data Based on ARIMA Model
ZHAO Zipeng, WEI Xinqi, TANG Long, GAO Bingfan, KANG Lianghe
(Gansu Agricultural University, Lanzhou" 730070, China)
Abstract: Due to the significant impact of weather on agricultural production, water resource management, and natural disaster prevention, it adopts the ARIMA model to achieve effective weather prediction. By using ACF and PACF diagrams to roughly determine the parameters of the ARIMA model, the optimal model is ultimately determined. ARIMA (1, 1, 1) is the daily minimum temperature model, with the residual sequence autocorrelation function and partial autocorrelation function basically falling within the 95% confidence interval. At the same time, the statistical results of Ljung-Box Q indicate that there is no correlation between residuals (P>0.05), indicating that residuals are white noise and satisfy the assumption of randomness. The final calculation errors (daily minimum temperature) RMSE, MAPE, and MAE are 2.63, 1.22%, and 2.06, respectively. The prediction results are good, providing a feasible solution for predicting the weather in Dingxi.
Keywords: weather forecasting; time series interpolation method; ARIMA model
0" 引" 言
定西市明清时期就已十年九旱,“贫瘠甲于天下”,
当地百姓经常遭受由灾害带来的死亡威胁和经济损失[1],所以准确预测和解读天气变化趋势对于农业决策[2]、灾害预防、人类的日常生活和经济活动[3]等方面具有重要意义。本研究的目标是利用ARIMA(Autoregressive Integrated Moving Average)模型来预测定西的天气趋势。ARIMA模型是一种常见的时间序列分析方法,通过分析历史数据中的趋势、周期性和随机性,可以预测未来的趋势。
张梓[4]建立了ARIMA(0,1,1)模型,预测了贵州省未来5年的增长趋势,结果表明相对相对误差较小。谢淑红等人[5]使用ARIMA模型得出苏州地区临床红细胞类血液需求预测研究的最优模型为ARIMA(0,1,1),且预测值均在95%CI内,平均相对误差较小,为8.21%,模型预测效果较好。吴会会等人[6]建立了一个ARMA(1,3)模型,并利用该模型预测了未来5年全球气表温度改变量,结合实验结果,分析了气候改变给人们带来的影响,最后给予了应对全球气候变暖的建议。满粟萌等人[7]建立了ARIMA(0,2,1)模型,运用该模型预测甘肃省5年内的城镇居民人均可支配收入,相对误差保持在0.03以下,拟合效果较好。结果显示:2022—2026年甘肃省城镇居民人均可支配收入呈现出持续上涨的趋势。Ariff等人[8]建立一个ARIMA(2,1,1)(0,1,0)预测新发结核病病例的模型,结果表明新发结核病例具有明显的季节性。Zhao等人[9]利用洛阳市1973至2021年逐月历史降水数据构建模型,采用ARIMA模型预测低频序列部分,对未来降水的预测结果具有较高的置信度。郑艳妮等人[10]建立了ARIMA(0,0,1)(2,1,1)_(12)模型其预测值与观测值整体趋势变化一致,绝对误差最小0.16、最大11.68。
ARIMA模型的优势在于它可以充分利用历史数据,自动调整模型参数以适应不同时间尺度的变化特征,并提供未来天气变化的概率分布,有助于风险评估和制定相应的应对措施。通过本研究,我们希望能够为定西的农民、水资源管理者和灾害预防机构提供有价值的参考,帮助他们更好地应对不可预测的自然环境变化,并推动天气预测技术的进一步发展。
1" 基本资料和算法原理
本文以甘肃省气象局2017—2021年的定西市天气数据为研究对象,数据中包括日降水量(mm)、日平均相对湿度(%)、日平均风速(m/s)、日平均气压(hPa)、日最高气温(℃)、日最低气温(℃)。我们以日最低气温为例。使用Python语言建立ARIMA模型。
ARIMA模型包括自回归(AR)、差分(I)和移动平均(MA)三个部分,通过调整这三部分的参数,可以得到不同的ARIMA模型:
式(1)中,yt表示当前值,α表示常数项,p表示自回归项,yi表示自相关系数,ε表示残差序列,q表示移动平均项,θ表示移动平均项系数。
ACF是衡量时间序列数据中自相关的度量,它可以用来确定q值(移动平均项的阶数)。PACF是衡量时间序列数据中偏自相关的度量,它可以用来确定p值(自回归项的阶数)。
式(2)中,k表示间隔的阶数,p表示AR(p)模型中的阶数。
ACF:
式(3)中,yt表示时间序列中的第t个值, 表示时间序列的平均值,k表示时间序列中的滞后期,n表示时间序列的长度。
均方根误差(Root Mean Square Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)及平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)公式如下:
2" 模型构建
2.1" 数据预处理
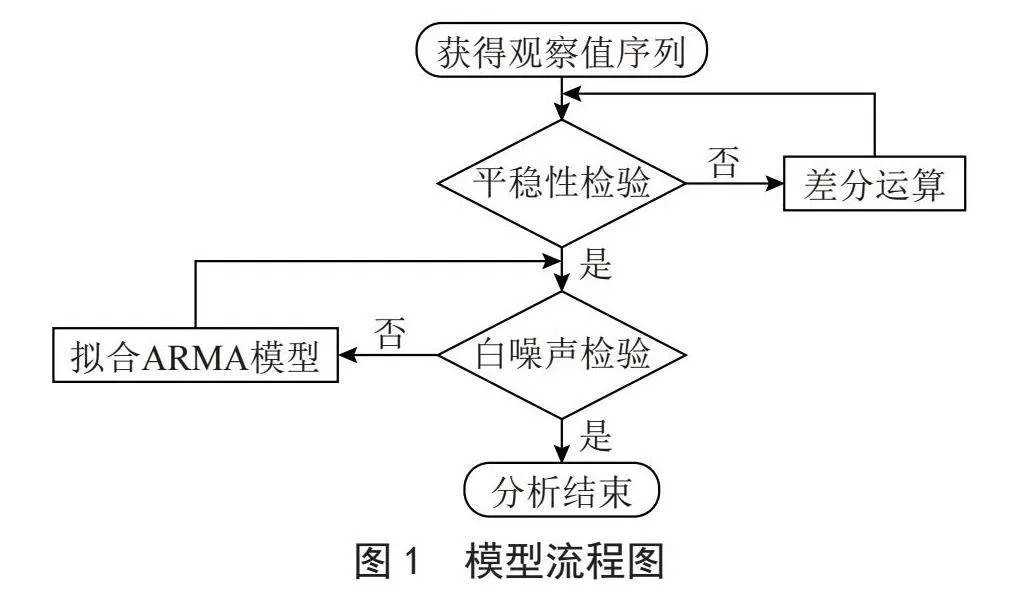
在ARIMA模型中,要求时间序列数据是平稳的且不符合白噪声假设。因此,在进行预测之前,我们需要对数据进行预处理。下面是对时间序列数据进行预处理的一般流程,如图1所示。
2.1.1" 缺失值处理
通过散点图对异常值检测发现数据里有缺失值,其统计共有63处,针对数据中的缺失问题,使用Python中的SciPy库中的interpolate模块来进行线性插值的计算,从而补全缺失数据,减少偏差,确保统计分析可靠性,提高模型的准确性,使模型更好地对新数据做出预测。
2.1.2" 平稳性检测
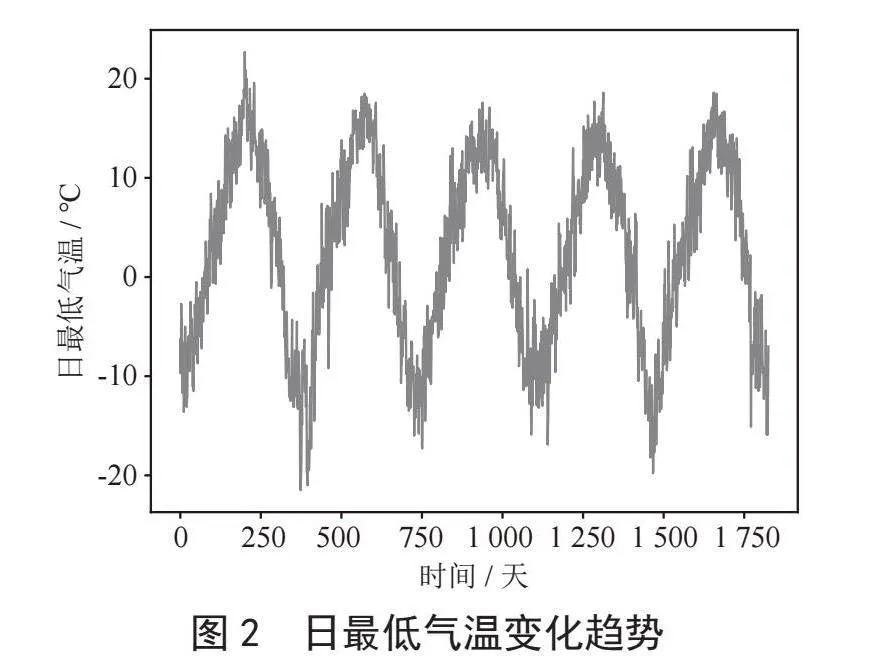
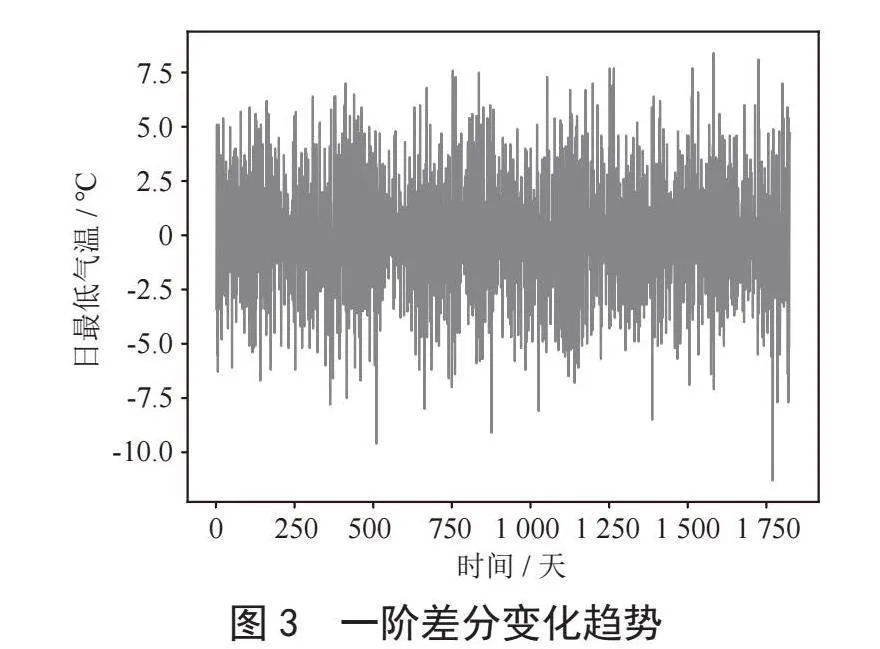
ARIMA模型是建立在对时间序列的平稳性要求上的,即只有平稳性的时间序列才适合于使用ARIMA模型进行分析和预测。平稳性的时序数据具有如下特点:均值稳定不变、随机性强、方差是恒定的。而且自相关系数只依赖于时间间隔,与时间的大小无关。如图2所示,很明显发现源数据不具有平稳性,因此进行差分处理。
差分处理后如图3所示,通过观察,数据的整体趋势不明显,不具有明显的季节性或周期性变化,则一阶差分具有平稳性。为了预测结果的准确性,因此我们采用一阶差分。
2.1.3" 白噪声检测
白噪声是指一个随机序列,在时间上没有自相关性,即不同时间点之间没有相关性。如果数据序列符合白噪声的假设,意味着序列中的数据相互之间是独立的,没有包含任何有用的信息。因此,在建模前,需要确保数据序列具有一定程度的自相关性。
为了检验差分序列是否满足白噪声的假设,利用Ljung-Box检验。该检验方法会计算一组滞后期的自相关系数,并基于这些系数进行统计检验,以确定序列是否表现出显著的自相关性。在白噪声检验中,我们通常关注的是检验的p值。
结果表明p值为4.907 389×10-22,几乎趋近于0,说明差分序列不满足白噪声的假设。也就是说,在差分序列中存在一定的自相关性。
2.2" 模型定阶
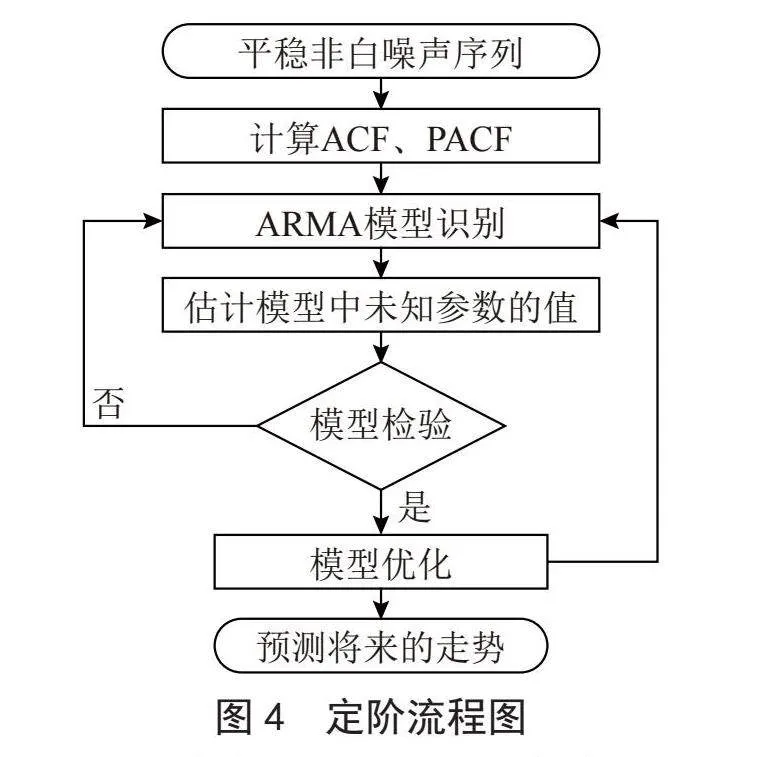
数据预处理工作完成后,通过计算ACF和PACF来确定ARIMA模型的阶数(p,d,q),详细流程如图4所示。
使用Python中的statsmodels库中的plot_acf()和plot_pacf()函数和matplotlib库来绘制ACF和PACF图,帮助分析时间序列数据的自相关性和偏自相关性。
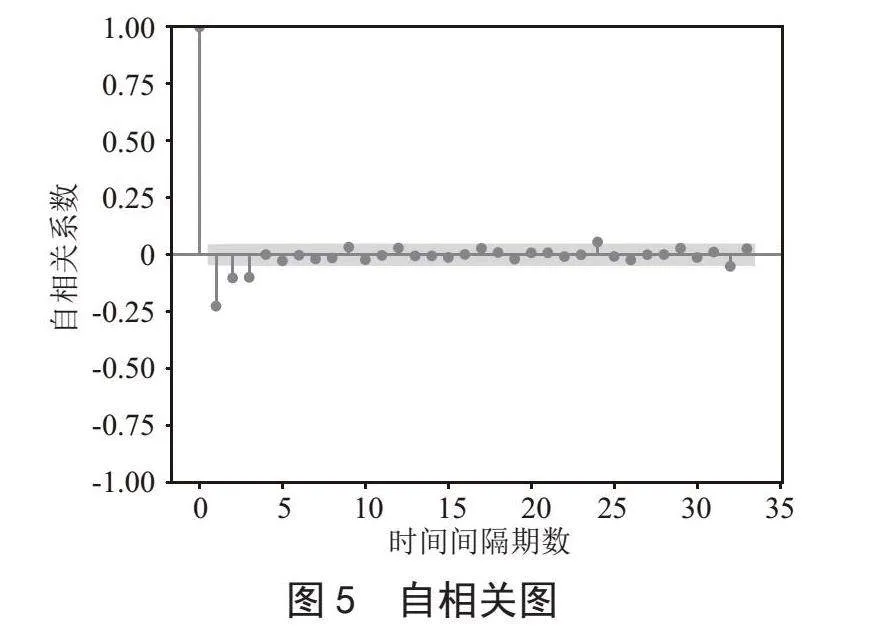
图5是自相关图:自相关图显示数据点之间的自相关性。该图显示了自相关系数与滞后(Lag)之间的关系。自相关系数衡量了数据与它自身之间的相关性。如图5所示,自相关图显示了在4阶以后数据点逐渐进入二倍标准差区域,具有拖尾(tail-off)特征。拖尾意味着数据点之间的相关性在滞后增加时逐渐减弱。这表明可以考虑使用自回归(AR)模型,因为拖尾特征通常与AR模型相关。
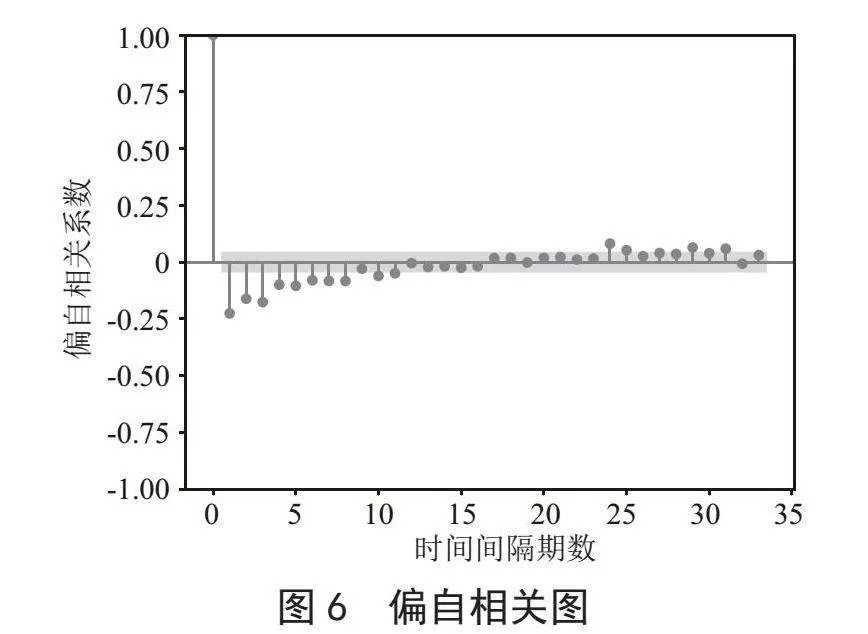
图6是偏自相关图:偏自相关图显示了两个数据点的相关性,消除了中间滞后项的影响。它们用来确定自回归部分(AR)和移动平均部分(MA)的滞后阶数。如图6所示,偏自相关图显示了9阶截尾(truncation)特征。截尾意味着滞后大于9的相关性趋近于零。这表明在滞后为9之后,偏自相关系数很小,可以考虑使用MA模型。
综合自相关图和偏自相关图的特征,且通过进一步的调整和验证,最终确定p = 1,q = 1,由于我们使用的是一阶差分后的数据,所以确定ARIMA(p,d,q)模型为ARIMA(1,1,1)。其中,p = 1代表自回归部分的滞后阶数,q = 1代表移动平均部分的滞后阶数,d = 1代表使用一阶差分来进行数据的平稳化。
2.3" 模型预测和误差分析
2.3.1" 模型预测
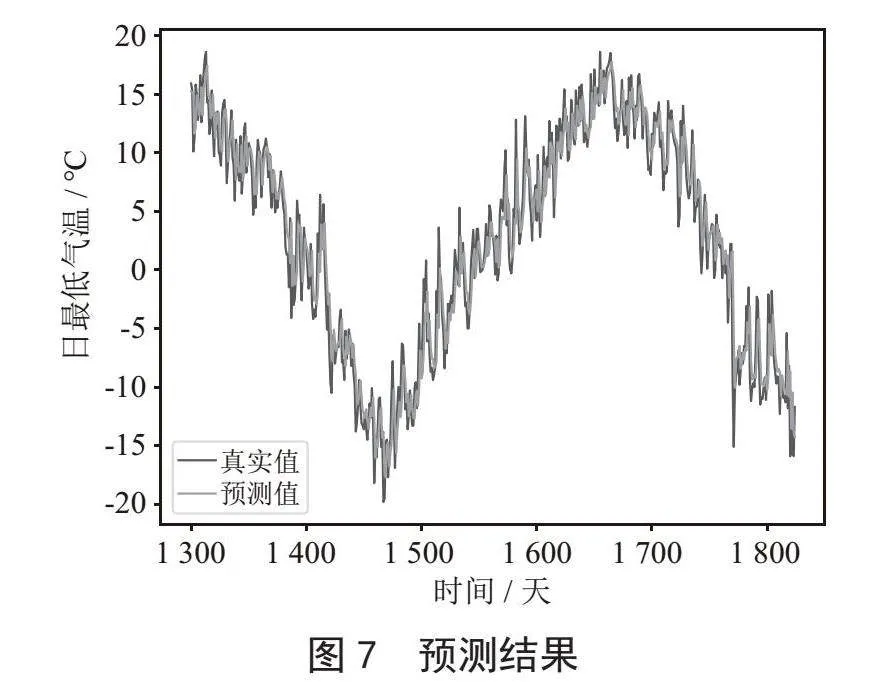
运用ARIMA(1,1,1)模型对2017—2021年的定西市天气数据为研究对象进行预测(以日最低气温为例),我们将70%的数据作为训练集X_train,剩余30%数据作为测试集X_test,得出预测值与实际值时序值拟合图,如图7所示。
从预测值和实际值的对比可以看出,预测结果和真实值拟合度较高。预测值基本围绕真实值上下波动,总体而言预测效果不错,模型能够较好地预测未来最低气温的变化趋势。
2.3.2" 误差分析
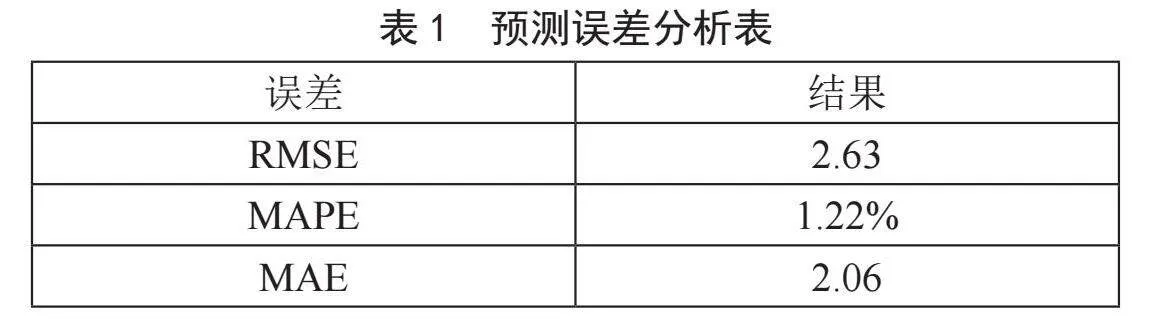
本文选择均方根误差(RMSE)、平均绝对误差(MAE)及平均绝对百分比误差(MAPE)作为评价指标。
表1结果表明,RMSE和MAE的值相对较低,说明预测结果整体上具有较好的准确性。模型的平均误差较小,预测值与真实值之间的差异较小。这意味着模型能较为准确地进行预测,捕捉到真实数据中的一些趋势和变化。
MAPE的值为1.22%,说明相对误差平均较小。意味着模型的相对误差不高,能够较为准确地预测出数据的相对变化。较低的MAPE值表示模型对真实数据具有较好的拟合度。
通过预测结果误差分析,可以认为该模型的预测效果较好。模型的预测准确性较高,平均误差较小,并能较好地捕捉到真实数据的趋势和变化。
3" 结" 论
以日最低气温为例,对未来数据进行预测,并获得了令人满意的预测结果。可以为定西的农民、水资源管理者和灾害预防机构提供宝贵的参考信息。对于农民而言,可以帮助他们做出合理的农作决策,如农作物的种植时间、灌溉计划等,以最大限度地优化农作物的产量和质量。对于水资源管理者而言,这一预测结果将有助于合理规划水资源的利用和分配,以适应不同气温条件下的需求和减少水资源的浪费。此外,对于灾害预防机构而言,这一预测结果将为他们提供重要的参考,以便提前预防自然灾害(如寒潮、霜冻等)给定西带来的经济损失。因此,这项预测研究的成功将为定西的社会经济发展和环境可持续性提供有力支持,帮助相关部门和决策者做出正确的决策。
通过上述同样的方法,我们对日降水量、日平均相对湿度、日平均风速、日平均气压、日最低气温也进行了建模。最终确定最优模型为ARIMA(3,1,2)为日降水量模型、ARIMA(1,1,1)为日最高气温模型、ARIMA(1,1,2)为日平均气压模型、ARIMA(2,1,2)为日平均风速模型、ARIMA(1,1,2)为日平均相对湿度模型。预测结果表明,预测值基本围绕真实值上下波动,总体而言预测效果不错。
参考文献:
[1] 权琦.明清时期定西自然灾害研究 [D].兰州:兰州大学,2007.
[2] 高淑敏.天气新闻对农业生产的重要性及影响 [J].农业灾害研究,2021,11(10):64-65.
[3] 田国萍.温度变化对我国农业经济的影响研究 [D].成都:西南财经大学,2021.
[4]张梓.基于ARIMA模型的贵州省GDP分析与预测 [J].国土与自然资源研究,2022(5):39-41.
[5] 谢淑红,张思静,严伟斌,等.基于ARIMA模型的临床红细胞类血液需求预测研究 [J].蚌埠医学院学报,2023,48(5):633-636.
[6] 吴会会,王嘉鹏,吴文静,等.基于ARIMA模型的全球气表温度预测分析 [J].现代信息科技,2023,7(16):147-150.
[7] 满粟萌,牛飞亮.基于ARIMA模型的甘肃省城镇居民人均可支配收入分析与预测 [J].投资与合作,2023(7):89-91.
[8] ARIFF M R A,RAFDZAH Z A,ROZITA W M W,et al. Forecasting New Tuberculosis Cases in Malaysia: A Time-Series Study Using the Autoregressive Integrated Moving Average (ARIMA) Model [J/OL].Cureus,2023,15(9):44676[2023-09-26].https://www.cureus.com/articles/170914-forecasting-new-tuberculosis-cases-in-malaysia-a-time-series-study-using-the-autoregressive-integrated-moving-average-arima-model#!/.
[9] ZHAO J W,NIE G Z,WEN Y H. Monthly precipitation prediction in Luoyang city based on EEMD-LSTM-ARIMA model [J].Water Science and Technology,2023,87(1):318-335.
[10] 郑艳妮,李盛,赵玉锐,等.武威市手足口病流行病学特征分析及ARIMA预测 [J].疾病预防控制通报,2023,38(4):10-14+68.
作者简介:赵子鹏(2002—),男,汉族,甘肃天水人,本科在读,研究方向:机器学习;魏新奇(2003—),男,汉族,甘肃会宁人,本科在读,研究方向:数据挖掘;唐龙(2001—),男,汉族,四川蓬安人,本科在读,研究方向:数据挖掘;高丙翻(2001—),女,汉族,甘肃白银人,本科在读,研究方向:机器学习;通讯作者:康亮河(1987—),女,汉族,甘肃会宁人,助教,硕士,研究方向:人工智能算法研究。