

摘 要:当下饮用水标准不断提高,传统水质预测方法存在明显不足。对使用循环神经网络(RNN)处理时间序列数据进行了研究。主要针对全年数据、夏季数据、冬季数据进行分析,结果显示全年数据最优模型MSE和MAE为0.004 7、
0.054 1;冬季数据最优模型MSE和MAE为0.005 1、0.054 4;夏季数据的模拟效果相对较差,其最低MSE和MAE值为
0.285 9、0.470 4。说明RNN在对大量的水质数据进行预测时,其模拟有效且拟合精度很高,但对数据量少、数据情况复杂的模型模拟时,其拟合效果并不是很好。
关键词:过滤水质预测;循环神经网络;时间序列;最优模型
中图分类号:TP18 文献标识码:A 文章编号:2096-4706(2024)14-0140-05
Research on the Filtration Process of Water Plants Based on RNN
ZHANG Weixi, HONG Lei
(School of Environmental and Municipal Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)
Abstract: The current drinking water standards are constantly improving, and traditional water quality prediction methods have obvious shortcomings. A study is conducted on the use of Recurrent Neural Networks (RNNs) for processing time series data. The analysis mainly focuses on annual data, summer data and winter data, and the results show that the optimal model MSE and MAE models for annual data are 0.004 7 and 0.054 1, respectively. The optimal model MSE and MAE for winter data are 0.005 1 and 0.054 4, respectively. The simulation effect of summer data is relatively poor, with the lowest MSE and MAE values of 0.285 9 and 0.470 4. It shows that when RNN is used to predict a large amount of water quality data, its simulation is effective and the fitting accuracy is high. However, when simulating models with small amounts of data and complex data situations, the fitting effect is not very good.
Keywords: filtration water quality prediction; Recurrent Neural Networks; time series; optimal model
DOI:10.19850/j.cnki.2096-4706.2024.14.029
0 引 言
水是人们生存必不可少的资源,随着科技的发展,人们对生活品质的要求也越来越高。饮用水与人的生命健康息息相关,饮用水的安全也成了人们健康生存的基本保障[1]。
随着计算机和人工智能等新一代技术的广泛应用,传统自来水厂在数字化转型和工业4.0的大背景下,将经历一次前所未有的深刻变革[2]。未来水厂建设的目标是进一步提高水厂运行的安全性和可靠性,同时降低能耗和用水量,以保证供水质量。未来自来水厂的相应设计应具备以下四个关键特征:净化单元的模块化、净化过程的“绿色化”、回收材料的再利用、控制方式的智能化[3]。
在水质数据处理中,传统的处理方法往往只适用于基本线性和动态特性不随时间变化的情况,而机器学习能够很好地反映过滤过程中众多变量之间存在的复杂非线性关系。机器学习就是通过计算机来模拟人类学习的一种算法,是人工智能的一个重要分支。人工神经网络是一种可用于处理具有多个输入节点和多个输出节点的实际问题的网络结构,是实现机器学习的一种模型。
1 RNN模型及建模流程
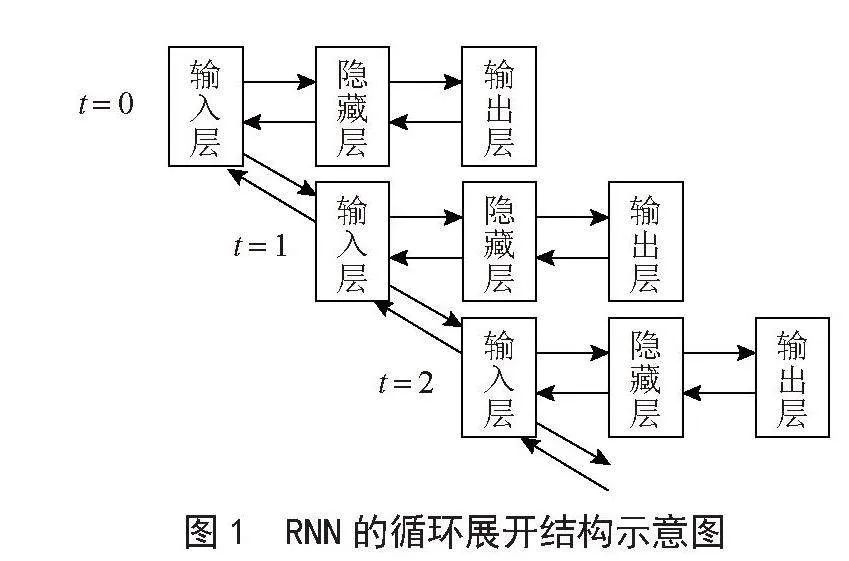
循环神经网络(RNN)是一种递归神经网络,常用来进行关于时间序列问题的数据建模[4-5]。循环神经网络的内部结构与普通神经网络不同,除了前向反馈和后向反馈,在其输入数据时不仅有当前时刻的输入,还有上一时刻的输出,通过内部循环的方式,将内部的神经网络多次利用,将时间序列数据中的关键信息持久化、记忆化,使其拥有较强的处理时间序列的能力[6]。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中,即隐藏层之间的节点不再是无连接而是有连接的[7]。RNN模型的循环展开结构示意图如图1所示。
从图1可看出,RNN隐藏层通过时间序列连接在一起,第一层表示t = 0时刻,第二层表示t = 1时刻,以此类推直到模型的时间步长。虽然RNN也通过反向传播实现梯度下降,但反馈方式与其他神经网络有所不同。RNN会将误差反馈到过去,某一时刻误差输出的梯度是由来自输出层的梯度与下一时刻反馈回来的输出的误差之和组成,这样网络就可以通过对全部时刻的误差进行反馈计算梯度,对权重和偏置进更新。
本文在RNN的建模中采用的底层数据库是基于TensorFlow的Keras框架建立的水质预测模型,具体编程语言为Python,编辑工具采用了Jupyter Notebook。而建立RNN模型可分为五个步骤[7]:
1)划分训练集与测试集。
2)参数设置。
3)模型训练。
4)模型评估。
5)最优模型预测。
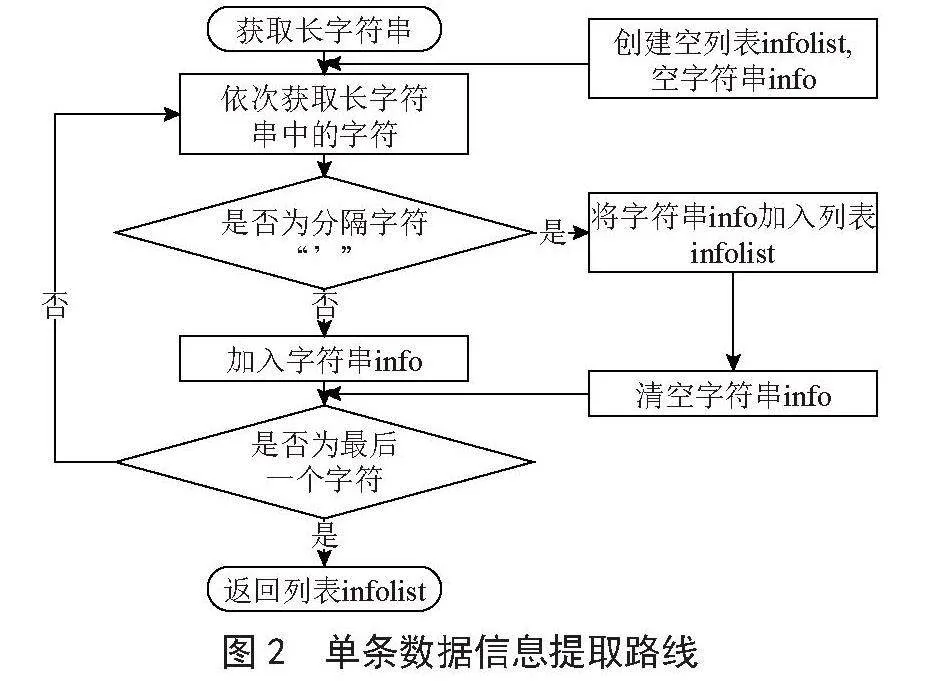
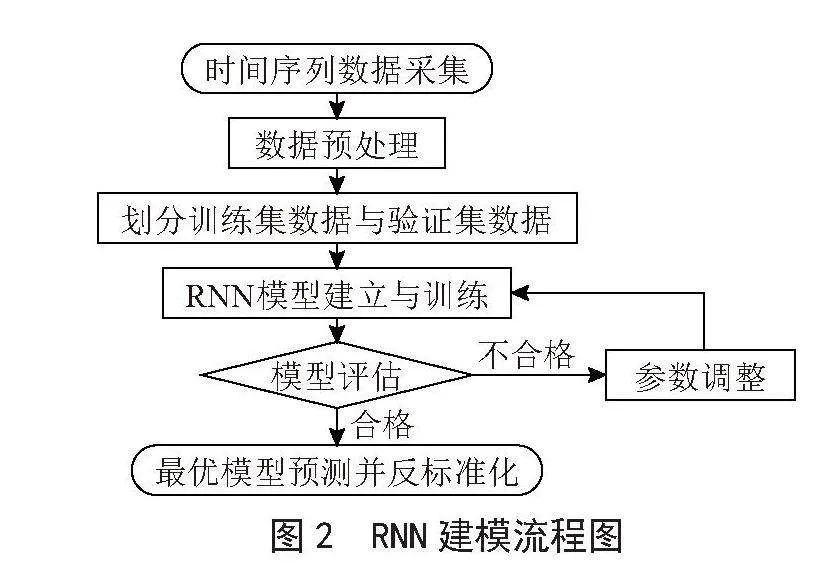
RNN的建模流程如图2所示。
2 数据采集与处理
2.1 数据采集
本文采集的数据是西北某水厂2022年12个月每日的水质数据,共365组数据。采集的水质数据有进水流量、温度、pH、过滤时间、进水浊度、出水浊度、混凝剂投加量、消毒剂投加量、余氯等水质指标。根据本文的要求,所需要的水质数据分别是滤池进水流量、温度、pH、过滤时间、进水浊度、出水浊度。由于模拟时的数据是单个过滤池的进水流量,因此要将单池流量计算出来,即总流量除以滤池个数,然后把这些数据摘选出来并存在新的Excel表格中。
2.2 数据预处理
2.2.1 缺失值处理
在对任何缺失的水质时间序列数据进行插补之前,需要考虑的重要问题是数据的缺失率及其可能存在的缺失规律,缺失率是指缺失的数据占总数据的比例。结合水质时间序列缺失的实际情况和相应的插补研究。本文的数据缺失值极少,只有个别数据缺失,属于轻微缺失。故采用算术平均值插补法处理缺失值[8]。
2.2.2 数据归一化
归一化方法有两种形式,一种是把数变为(0,1)之间的小数,一种是把有量纲表达式变为无量纲表达式。主要是为了数据处理方便而提出来的,把数据映射到0~1范围之内处理,会更加便捷快速[9]。
数据的不同表现形式通常会对模型训练产生不同的影响,而原始数据中的特征属性列之间各自都有不同的单位(量纲),如m3/h、NTU、℃等,并且大小差异很大,导致属性间不可比较,为了消除量纲带来的负面影响,需要对数据各节点做归一化处理,本论文选用min-max归一化。公式如下:
(1)
式(1)中n表示对应的属性,即流量、温度、pH等;i表示数据的编号;xni表示某一属性归一化后的数值;xi表示某一属性的数据;xmin表示该属性数据中的最小值,xmax表示该属性数据中的最大值。归一化后的数据会在(0,1)之间,可以加快模型的收敛速度,并且有助于提高模型的预测精度。
2.2.3 划分训练集与测试集
本论文采集的数据共有365组,按照训练集数据与测试集数据的比例为3:1来划分,即训练集数据有273个,测试集数据有92个。
又考虑到温度对水质数据有很大的影响,故分别将夏季与冬季的时间序列数据单独拿出来进行训练。夏季采集5、6、7、8月的数据进行训练,共有123组数据,按照训练集数据与测试集数据的比例为3:1来划分,即训练集数据有92个,测试集数据有31个。冬季采集12、1、2、3月的数据进行训练,共有121组数据,按照训练集数据与测试集数据的比例为3:1来划分,即训练集数据有90个,测试集数据有31个。
3 检测结果与分析
3.1 模型评价指标
检验过滤效果的指标为均方误差(Mean Squared Error, MSE)[10]和平均绝对误差(Mean Absolute Error, MAE)[11]。
3.1.1 均方误差
均方误差主要是用于解决回归问题的损失函数。公式如下:
(2)
式(2)中MSE表示均方误差向量组,y表示预测值的向量组, 表示实际值的向量组,下标i表示向量组中第i个数据。
3.1.2 平均绝对误差
平均绝对误差是所有单个观测值与算术平均值的偏差的绝对值的平均。与平均误差相比,平均绝对误差由于离差被绝对值化,不会出现正负相抵消的情况,因此平均绝对误差能更好地反映预测值误差的实际情况。公式如下:
(3)
式(3)中MAE表示平均绝对误差向量组,y表示预测值的向量组, 表示实际值的向量组,下标i表示向量组中第i个数据。
3.2 测试集模拟结果
本文提出了基于RNN的过滤水质预测模型,为提高预测的准确度,会先对模型的隐藏层数进行选择,然后在实验中不断调整时间步长t、各隐藏层神经元个数、网络迭代次数epochs和批量大小以达到最佳预测性能。最后通过MSE和MAE值进行性能比较,找到最优预测模型。
3.2.1 全年数据建立RNN模型
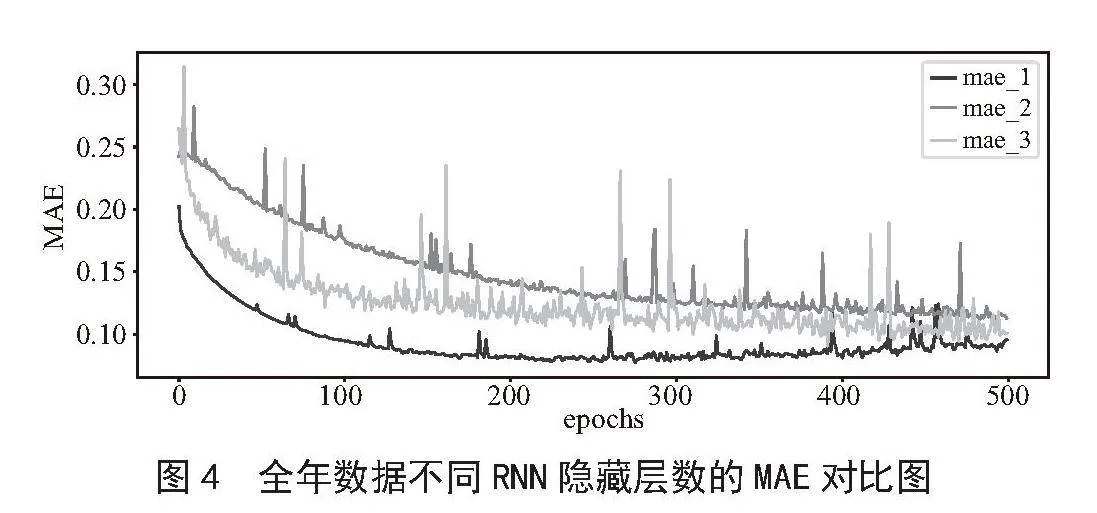
定义其初始时间步长为30,隐藏层为分别设置1层、2层和3层,隐藏层神经元数为128,激活函数使用tanh,优化器使用SGD,学习率为0.001,设置训练轮数epochs为500,批次大小为30,然后使用Sequential进行建模。损失函数(loss)用均方误差(MSE)定义,度量指标(metrics)使用平均绝对误差(MAE)衡量。其不同RNN隐藏层的误差曲线图和MAE曲线图模拟结果如图3、图4所示[12]。
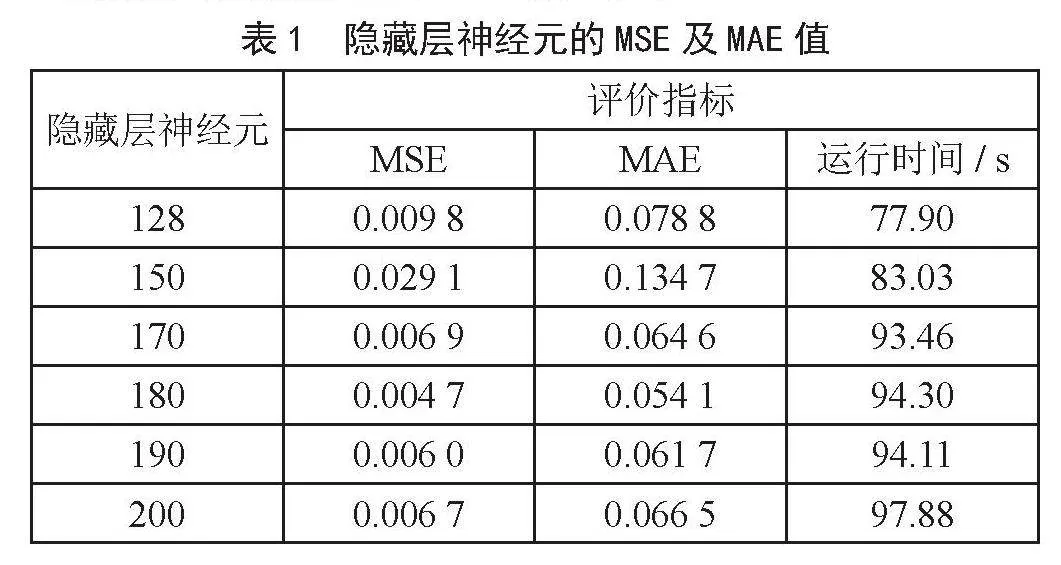
由图3、图4可知,不同隐藏层个数所训练模型的效果不同。根据误差曲线图和MAE曲线图显示,两个RNN隐藏层和三个RNN隐藏层时,其训练效果并不好,预测结果不稳定。而一个RNN隐藏层时,模型的误差很小,且曲线拟合效果好,其MSE和MAE分别为0.009 8、0.078 8。接下来会通过调节训练参数对模型进行优化。
由表1可看出,神经元为180时其MSE、MAE值最低,分别为0.004 7、0.054 1。
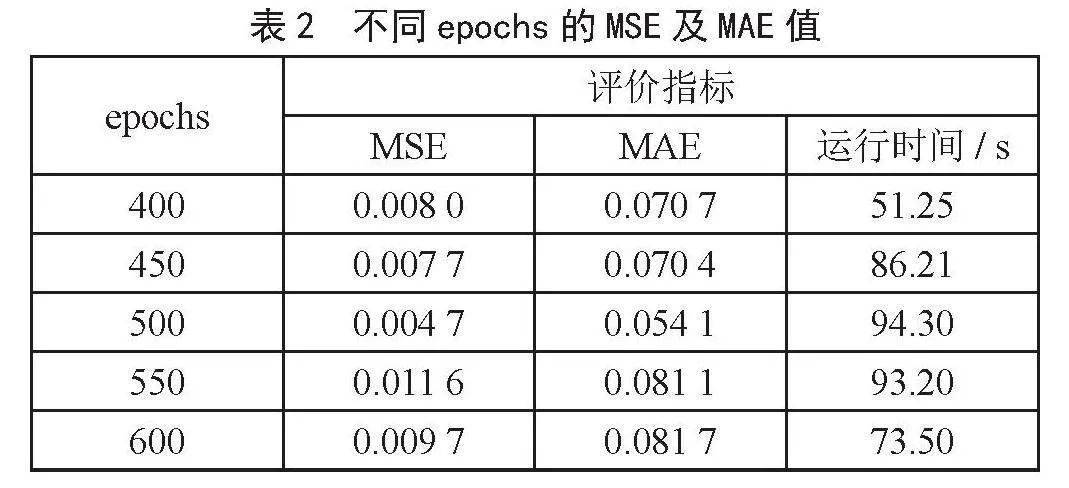
由表2可知,epochs为500时,模型拟合精度最
高,MSE、MAE值分别为0.004 7、0.054 1。时间步长t,批次大小的优化同表2,得到的最优时间步长为30,最优批次大小为30。
通过不断优化模型参数,得到的最优模型参数是时间步长为30、隐藏层神经元数为180、网络迭代次数epochs为500、批次大小为30。最优模型的MSE和MAE分别为0.004 7、0.054 1,运行时间为94.30 s,相比于最开始的0.009 8、0.078 8,MSE和MAE分别降低了0.005 1、0.024 7。
3.2.2 冬季数据建立RNN模型
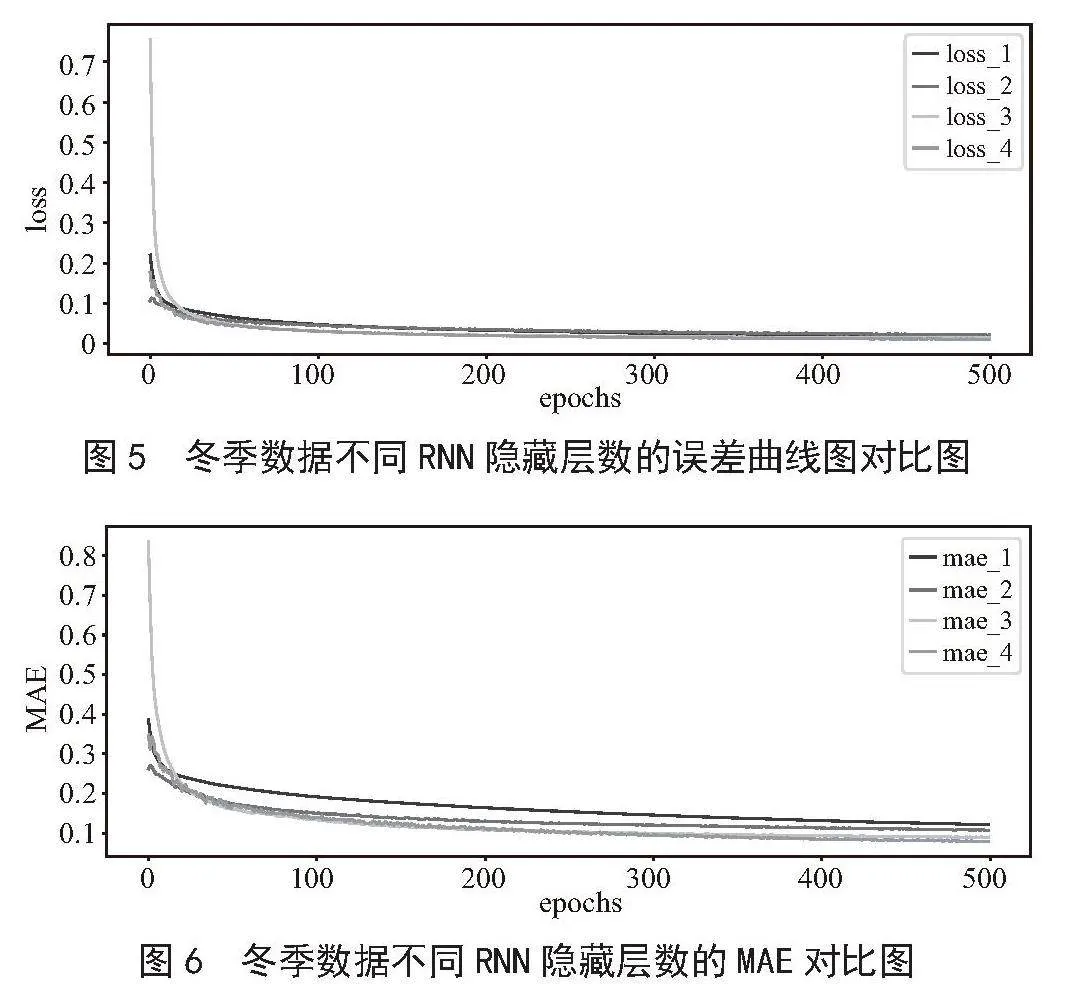
定义其初始时间步长为30,隐藏层为分别设置1层、2层、3层和4层,隐藏层神经元数均为64,激活函数使用tanh,优化器使用SGD,学习率为0.001,设置训练轮数epochs为500,批次大小为10。损失函数(loss)用均方误差(MSE)定义,度量指标(metrics)使用平均绝对误差(MAE)衡量。其不同RNN隐藏层的误差曲线图和MAE曲线图模拟结果如图5、图6所示。
由图5、图6可知,不同隐藏层个数所训练模型的效果不同。根据误差曲线图和MAE曲线图显示,当RNN隐藏层为3层和4层时其损失较小,曲线拟合效果更好。3层隐藏层其MSE为0.012 1,MAE为0.087 1,训练时间为71.08 s,4层隐藏层其MSE为0.008 7,MAE为0.073 6,训练时间为138.13 s。接下来会通过调节训练参数对模型进行优化。
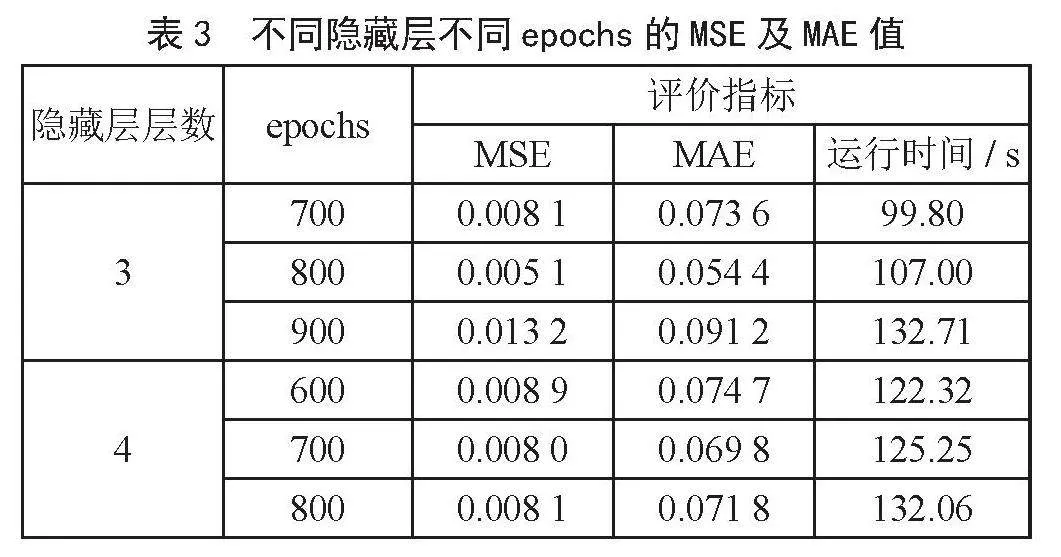
由表3可看出,当有3层隐藏层,epochs为800时其MSE、MAE值最低,分别为0.005 1、0.054 4。
神经元个数、时间步长、批次大小的参数优化同表3,得到最优参数是各隐藏层神经元为64,64,64,时间步长为30,批次大小为10。通过不断优化模型参数,最优模型的MSE和MAE分别为0.005 1、0.054 4,运行时间为107 s,相比于最开始的0.012 1,0.087 1,MSE和MAE值分别降低了0.007 0、0.032 7。
3.2.3 夏季数据建立LSTM模型
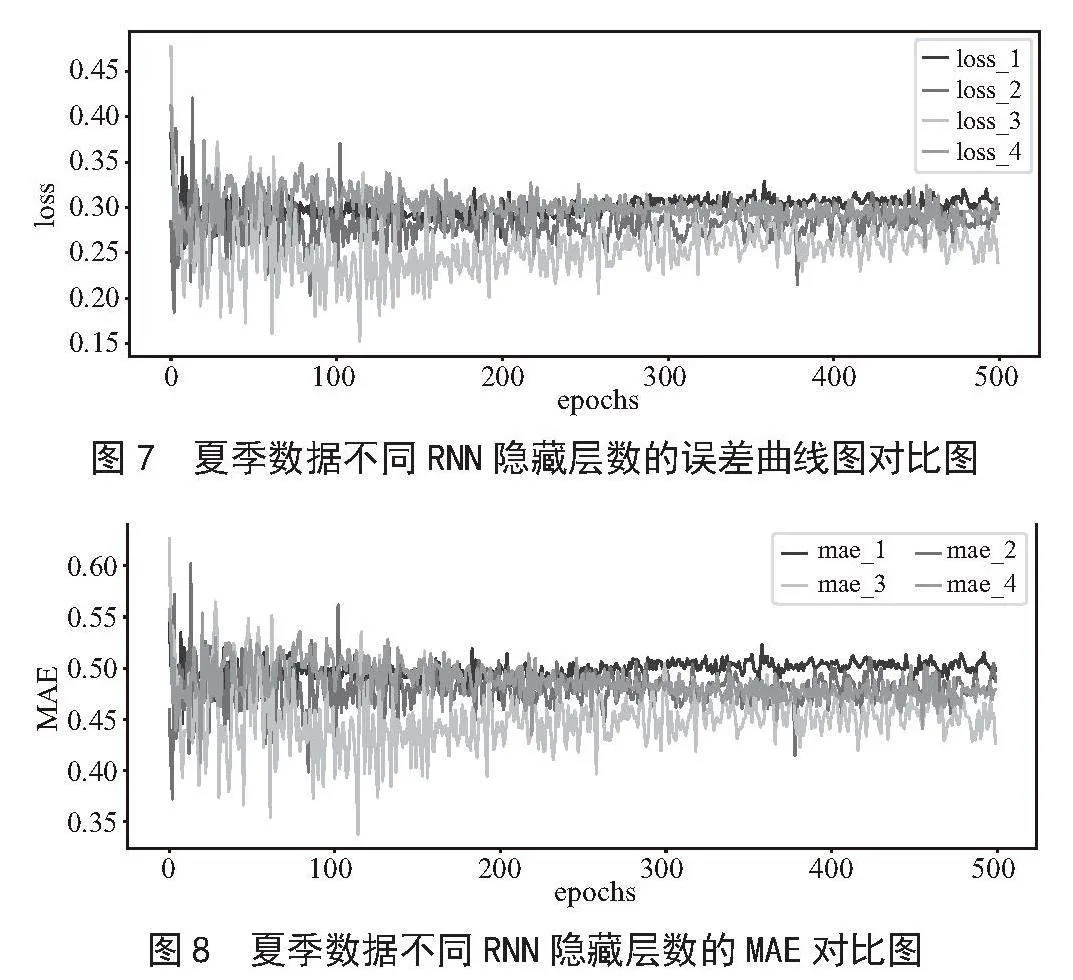
定义其初始时间步长为10,隐藏层为分别设置1层、2层、3层和4层,隐藏层神经元数均为64,激活函数使用tanh,优化器使用Adam,学习率为0.001,设置训练轮数epochs为500,批次大小为10。损失函数(loss)用均方误差(MSE)定义,度量指标(metrics)使用平均绝对误差(MAE)衡量。其不同RNN隐藏层的误差曲线图和MAE曲线图模拟结果如图7、图8所示。
由图7、图8可明显看出,在使用RNN神经网络对夏季数据进行模拟时,模拟效果非常差,其最低MSE和MAE值分别为0.285 9、0.470 4。
3.3 结果分析
通过对全年数据、夏季数据、冬季数据分别使用RNN进行模拟。可知全年数据模拟的最优模型参数是时间步长为30、隐藏层神经元数为180、网络迭代次数epochs为500、批次大小为30。最优模型的MSE和MAE分别为0.004 7、0.054 1,运行时间为94.30 s,相比于最开始的0.009 8、0.078 8,MSE和MAE分别降低了0.005 1、0.024 7。冬季数据模拟的最优模型参数是时间步长为30,各隐藏层神经元为64,64,64,批次大小为10。最优模型的MSE和MAE分别为0.005 1、0.054 4,运行时间为107 s,相比于最开始的0.012 1,0.087 1,MSE和MAE值分别降低了0.007 0、0.032 7。而夏季数据在使用RNN对夏季数据进行模拟时,模拟效果非常差,其最低MSE和MAE值分别为0.285 9、0.470 4。
说明同一个神经网络模型在模拟不同数据集时,其模拟效果也是不同的。如全年数据和夏季数据,两个数据集的模拟效果非常接近,但是全年数据的运行时间却比冬季数据的短,证明在使用RNN模型对数据集进行训练时,数据量越大,训练的迭代次数越少,训练的难度越小。而夏季数据的模拟效果之所以差,一是因为夏季的水质数据波动非常大,用少量的数据训练时,RNN无法捕捉其参数间的特征和规律;二是因为RNN模型结构还存在缺陷。
4 结 论
本文提出了一种基于RNN的水质预测方法,通过采集西北某水厂2022年一年的数据,对未来的出水浊度指标进行预测。可知在同一种数据类型不同数据量的情况下,RNN模型的拟合结果会存在差异:
1)全年数据和冬季数据的模拟效果非常接近,但是全年数据的运行时间却比夏季数据的短,说明RNN神经网络的数据量越大,训练的迭代次数越少,训练的难度越小。
2)在同样数据量,不同时间点的情况下,模型性能也会存在差异。相比于冬季数据集,夏季数据集的模型难以拟合,因为夏季的水质数据波动非常大,用少量的数据训练时,RNN无法捕捉其参数间的特征和规律。
由此说明,RNN在对大量的水质数据进行预测时,其模拟是有效的,且拟合精度也是非常高的,所以RNN对水厂未来的过滤水质预测是可行的,可以进一步提高净水厂智能化水平。但是当RNN模拟数据量少、数据情况复杂的模型时,其拟合效果并不是很好。所以,RNN更适合用于长期数据的模拟。
参考文献:
[1] 张金松,李冬梅.新《生活饮用水卫生标准》推动供水行业水质保障体系化建设 [J].给水排水,2022,58(8):6-12.
[2] 陆继诚.从“自动化”到“智慧化”——智慧水厂建设的新思路 [J].给水排水,2017,53(11):1-3.
[3] 孙凝,赵顺萍,解鹏,等.智慧水厂管理平台的研究与实践 [J].给水排水,2022,58(1):151-155.
[4] YU Y,SI X S,HU C H,et al. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures [J].Neural Computation,2019,31(7):1235-1270.
[5] 何诗扬,汪玲,朱岱寅,等.基于时空记忆解耦RNN的雷暴预测方法 [J].系统工程与电子技术,2023,45(11):3474-3480.
[6] 邹可可,李中原,穆小玲,等.基于LSTM-GRU的污水水质预测模型研究 [J].能源与环保,2021,43(12):59-63.
[7] 董云程.基于ARIMA-LSTM的城市供水量组合预测模型研究 [D].昆明:昆明理工大学,2021.
[8] 杨哲.基于GAN的智能气象网关数据补全技术研究 [D].上海:华东师范大学,2022.
[9] 唐亦舜,徐庆,刘振鸿,等.基于优化非线性自回归神经网络模型的水质预测 [J].东华大学学报:自然科学版,2022,48(3):93-100.
[10] 徐瑞.基于SARIMA-LSTM的北仑河口水质预测方法研究及应用 [D].重庆:重庆大学,2019.
[11] 谈昊然.深度—宽度学习模型及在降水量预测中的应用 [D].南京:南京信息工程大学,2022.
[12] CHO M,KIM C,JUNG K,et al. Water Level Prediction Model Applying a Long Short-Term Memory(LSTM)-Gated Recurrent Unit(GRU) Method for Flood Prediction [J].Water,2022,14(14):2221(2022-07-14).https://www.mdpi.com/2073-4441/14/14/2221.
作者简介:张维玺(1998.12—),男,汉族,陕西宝鸡人,硕士在读,研究方向:机器学习在水处理中的应用;洪雷(1971.10—),男,汉族,陕西咸阳人,副教授,博士研究生,研究方向:净水处理中的数据模拟。
收稿日期:2024-01-02