

摘 要:生产者价格指数(PPI)是衡量生产者支付的原材料、劳动力和其他生产成本的变化指标。对经济的稳定和企业的经营都有着重要的意义,可以帮助政府、央行和企业做出相应的决策和调整。文章选取2013年1月至2023年7月的PPI月度数据,建立了AMIMA(1,0,2)模型,并利用该模型对2023年1月至7月的PPI进行预测,随后,将预测结果与实际值进行了对比,结果显示,模型具有良好的预测效果,为未来6个月的PPI指数提供了可靠的预测,这一结果为制定经济政策提供了重要参考。
关键词:ARIMA模型;生产者价格指数(PPI);短期预测
中图分类号:TP391.1 文献标识码:A 文章编号:2096-4706(2024)15-0129-05
Prediction of Producer Price Index Based on ARIMA Model
TAO Yong, JIN Liangqiong, LI Qiongyi, SU Yanqing, ZOU Luyan, RAN Yejun
(School of Data Science and Information Engineering, Guizhou Minzu University, Guiyang 550025, China)
Abstract: Producer Price Index (PPI) is an indicator to measure the changes of raw materials, labor and other production costs paid by producers. It is of great significance to economic stability and enterprise management, and can help the government, central bank and enterprises make corresponding decisions and adjustments. This paper selects the monthly data of PPI from January in 2013 to July in 2023, establishes the AMIMA (1,0,2) model, and uses this model to predict the PPI from January to July in 2013. Then, the prediction results are compared with the actual values. The results show that the model has a good prediction effect and provides a reliable prediction for the PPI index in the next six months, which provides an important reference for formulating economic policies.
Keywords: ARIMA model; Producer Price Index (PPI); short-term prediction
0 引 言
生产者价格指数(Producer Price Index, PPI)是衡量工业企业产品出厂价格变动趋势和变动程度的指数[1]。从宏观层面看,PPI上涨会带来物价水平的上升,提高通货膨胀风险,导致货币政策加紧,利率上调,财政政策加码,以达到有效控制价格上涨的目的。从中观层面看,PPI上涨会使制造业原材料价格上涨,而产品物价却无法快速提升。此时,企业可能会面临产品利润率下降、产品竞争力占优、市场份额不断下降等问题。与此同时,为了降低成本企业可能会缩减固定成本、减少生产线投入或者减少员工的薪资、裁员等手段。从微观层面看,PPI上涨会直接影响到个人消费水平。当PPI上涨,生产厂家的生产成本一定程度上增加,此时生产厂家可能会提高售价来维持自身的利润,这样会导致商品价格上涨,进而影响到消费者的购物欲望,导致消费者的消费力随之下降,从而使得经济增长停滞。综上所述,PPI指数的上涨和下跌并不是一件孤立的事件,背后有着复杂的经济因素和趋势的影响。随着PPI指数的波动和变化,生产厂家、消费者、政府政策等方面都会受到不同程度的影响。因此,PPI的未来走势成为社会所关注的问题。
国内学术界对通货膨胀的预测方面积累了大量的研究成果,赵永兴利用EGARCH(1,1)模型研究中国PPI分类指数的波动情况;张立基于向量自回归模型研究生产者价格指数和居民消费价格指数之间的动态关系;董大勇等利用ARIMA模型对生产者价格指数进行了短期预测;何跃研究了PPI对GDP的预警作用,为宏观经济政策提供了依据。严彦文建立的AMIMA(1,1,1)模型具有良好的预测效果。Tang等人提出了基于模糊信息粒化的GA-SVR-ARIMA混合模型,旨在解决PPI估计中的不精确问题。乔宝华等人基于面板模型研究PPI上涨对我国工业经济的影响,并对如何有效推动中国工业经济的稳定发展给出建议。侯成琪、张怀强和杜军岗等学者也分别运用DSGE模型以及VAR模型等工具,对PPI和CPI的背离现象进行了研究和解释。然而,目前对PPI本身的走势进行分析和预测的文献较少,因此,本文选取我国的PPI月度数据,并建立ARIMA模型,以预测PPI的未来趋势。
1 ARIMA模型
本文通过建立ARMA(p,q)模型预测我国的生产者价格指数,ARIMA模型是一种时间序列分析模型,用于预测未来时间点的数值[2]。其基本思想是通过建立自回归(AR)和移动平均模型(MA),对时间序列数据进行建模和预测。该模型的原理是通过对时间序列数据进行差分操作,将非平稳的时间序列转换为平稳的时间序列[3],然后利用AR和MA模型来拟合数据的自相关性和移动平均性,从而进行预测。
1.1 ARMA模型
ARMA(p,q)模型一般表示为:
其数学表达式为:
引入延迟算子,ARMA(p,q)模型记为:
其中,为p阶自回归系数多项式;为q阶滑动平均系数多项式。
1.2 ARIMA模型
ARIMA(p,d,q)模型一般表示为:
式中,,为平稳可逆ARMA(p,q)模型的自回归系数多项式, 为平稳可逆ARMA(p,q)模型的移动平均系数多项式。
d阶差分后序列可以表示为:
式中,,即差分后序列等于原序列的若干序列值的加权和,对差分平稳序列可以拟合自回归移动平均模型,所以称为求和自回归移动平均模型[4]。
2 模型在生产者价格指数预测中的应用
2.1 数据来源
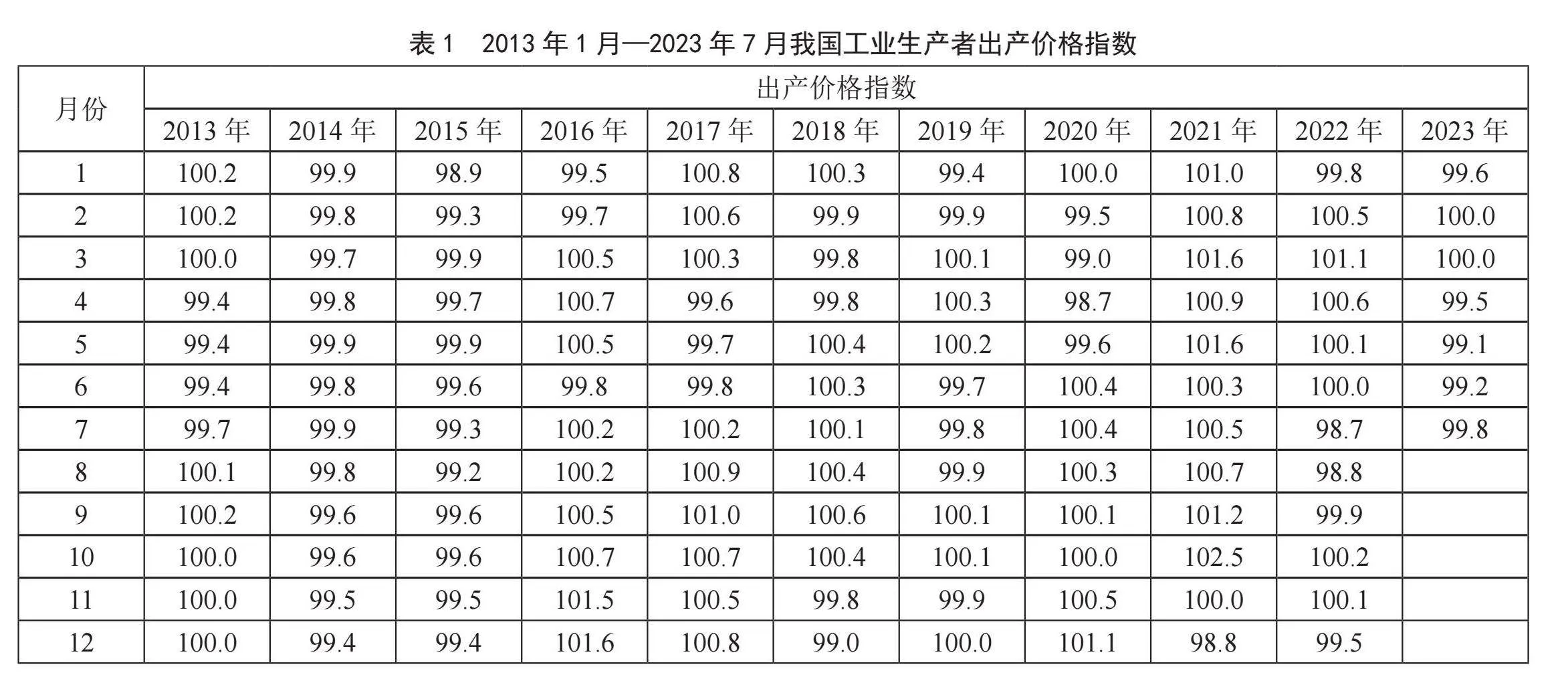
为了分析我国PPI变化趋势,本文选取2013年1月至2023年7月我国PPI的月度数据,数据从国家统计局网站获取,如表1所示。
2.2 数据平稳性检验
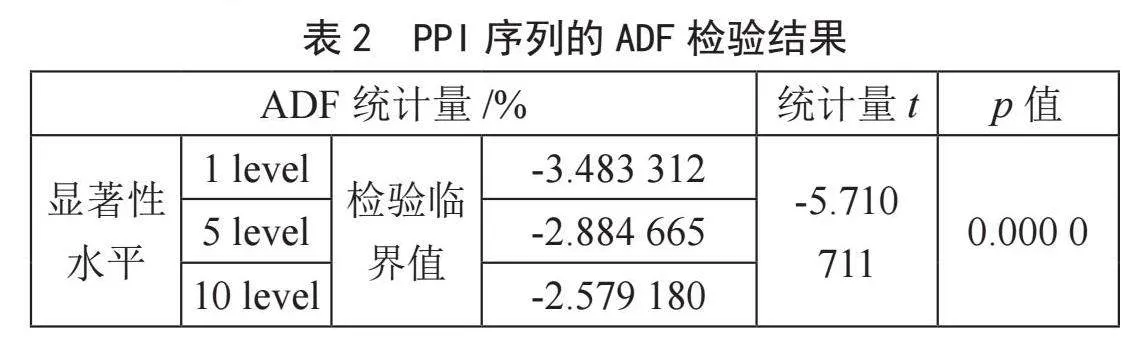
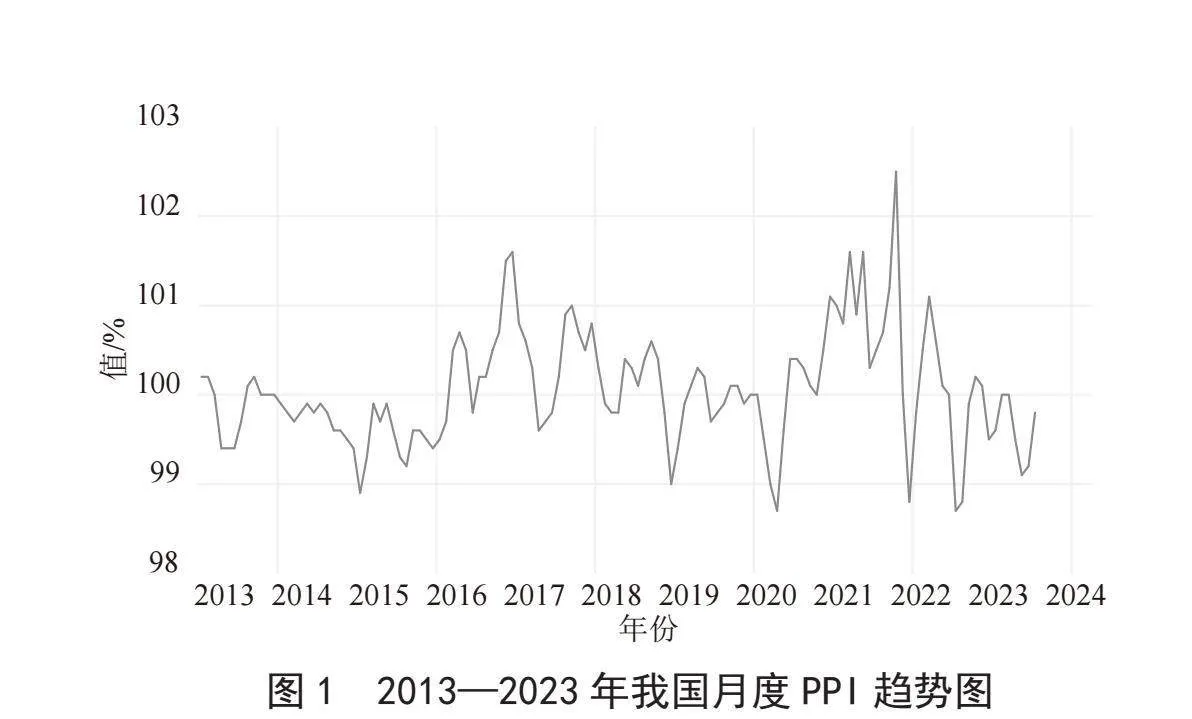
在使用ARIMA模型对PPI进行分析和预测之前,必须确保时间序列的稳定性。为此,需要进行单位根检验。单位根过程是指时间序列中存在的一种非平稳性质[5],通过单位根检验判断时间序列是否包含单位根,从而决定是否需要进行差分运算来使序列平稳。单位根检验可以采用多种方法,例如ADF检验、PP检验和NP检验等[6]。在本研究中,我们使用ADF检验,对我国2013年1月至2023年7月的月度PPI趋势分析,先绘制时序图进行平稳性检验,如图1所示。
通过使用Eviews软件对选取的数据进行ADF检验,如表2所示,p值为0.000 0(小于0.05),ADF检验的t值为-5.710 711,表明在显著性水平下,拒绝原假设,即时间序列是平稳的,这表明后续的实证分析可以使用ARIMA模型。
2.3 模型建立
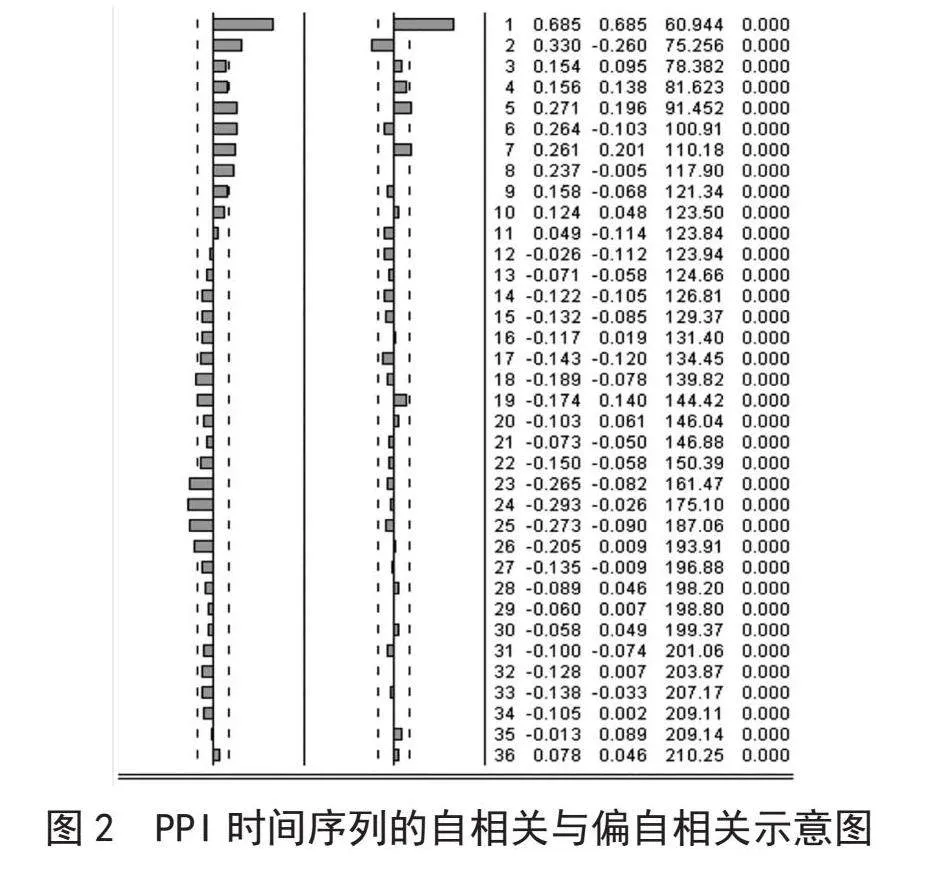
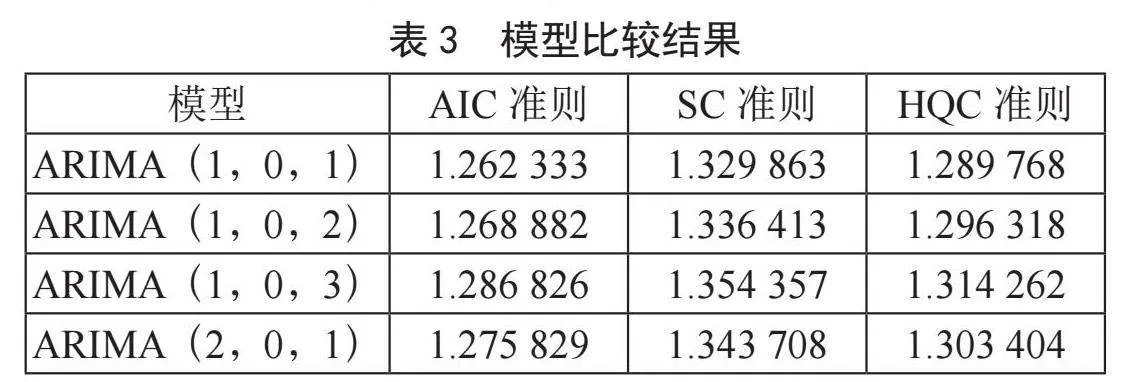
根据上文的ADF平稳性检验,不需要进行差分,即参数d=0。通过绘制自相关图和偏相关图来确定ARMA(p,q)模型中p和q的值,如图2所示。原始时间序列的自相关系数在滞后多阶后都落在随机区域内[5],且呈快速衰减趋势,表明序列PPI的趋势基本得到消除。PPI时间序列的偏自相关函数在滞后2阶超出了95%的置信区间[7],显著不为零,则p的取值为1或2。由于PPI时间序列的自相关函数在滞后2阶处仍显著不为零,所以我们考虑q的取值为1、2或3。因此,我们构建了ARIMA(1,0,1)、ARIMA(1,0,2)、ARIMA(1,0,3)和ARIMA(2,0,1)模型。
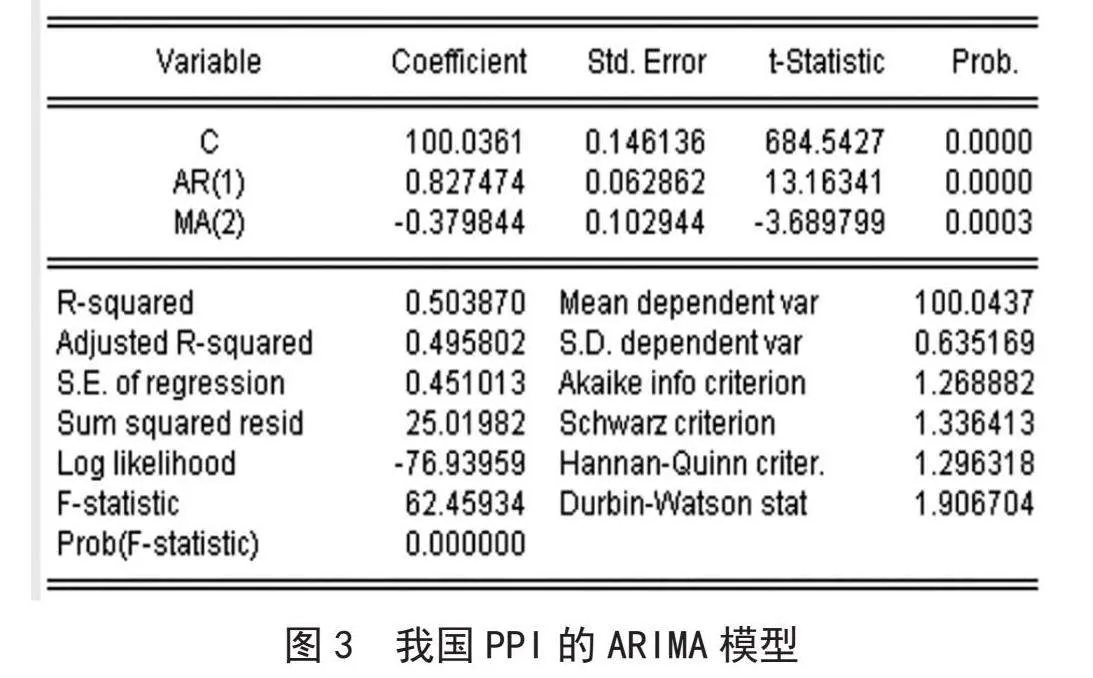
为了确定最终的模型结构,我们综合考虑了模型的整体效果,并使用AIC、SC和HQC准则对两个模型进行比较。比较结果如表3所示,我们发现ARIMA(1,0,2)模型的AIC值和SC值都小于ARIMA(1,0,3)和ARIMA(2,0,1)模型。最终选定ARIMA(1,0,2)模型,如图3所示。
由图3可得R2=0.503 870,信息量准则量AIC=1.268 882,SC=1.336 413,标准误差SE=0.451 013,DW=1.906 704,接近2,表明残差序列不存在自相关,则诊断出ARIMA(1,0,2)模型为最优模型。模型的具体形式为:
PPIt=100.036 1-0.827 474PPIt-1-0.379 844ut-2
2.4 模型的检验
2.4.1 模型平稳性检验
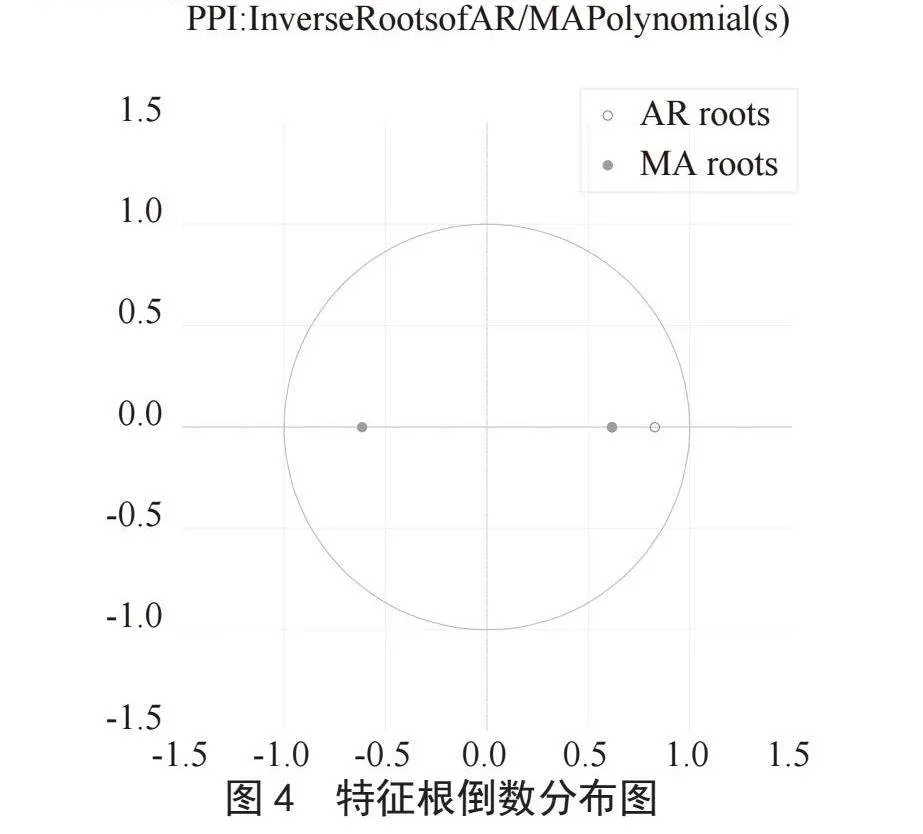
如图4所示,模型的特征根倒数均不超过1,且特征根倒数都位于单位圆内[8],这意味着本文所建立的模型具有良好的稳定性。
2.4.2 模型检验
如图5所示,为了进一步确认ARIMA(1,0,2)模型提取的数据信息是否有效,我们对该模型的残差进行白噪声检验[9]。
根据图5可以看出,ARIMA(1,0,2)模型的残差序列的自相关函数在95%的置信区间内[5],表明残差序列没有显著的自相关性,通过了白噪声检验[3],滞后1阶至36阶的P值都大于0.05,可以认为该模型的拟合效果较好[10]。
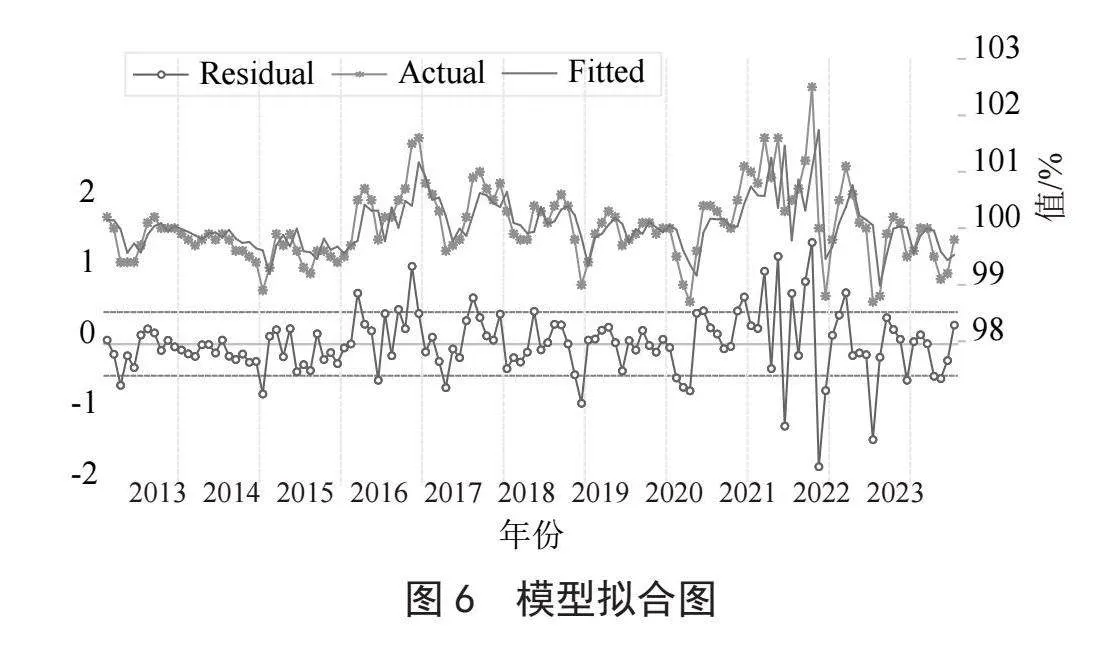
此外,为了进一步评估模型的拟合效果,我们绘制了模型拟合图,观察残差的波动范围,该模型的拟合值与实际值非常接近,表现出了良好的拟合效果。如图6所示,我国PPI指数在近十年相对稳定,但2020年新冠疫情的爆发导致我国PPI指数波动较大。随着疫情之后,PPI指数又开始逐渐趋向平稳。
2.5 模型的预测与分析
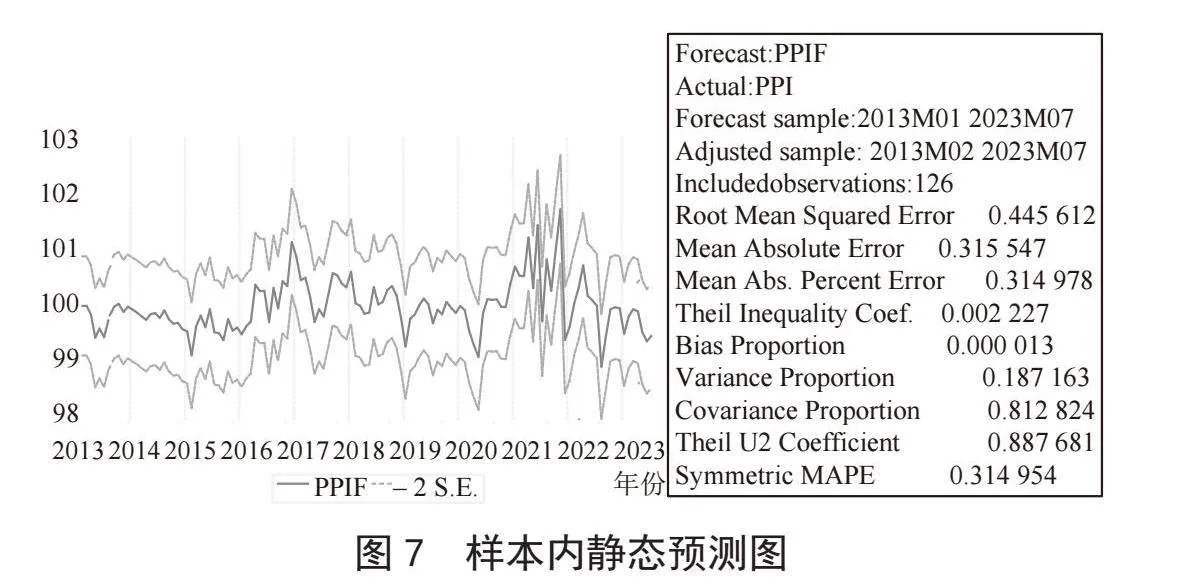
如图7所示,预测样本区间为2013年1月到2023年7月。据预测结果,我们可以得到Theil系数为0.002 227,协方差比例为0.812 824,表明模型的预测结果较为准确。
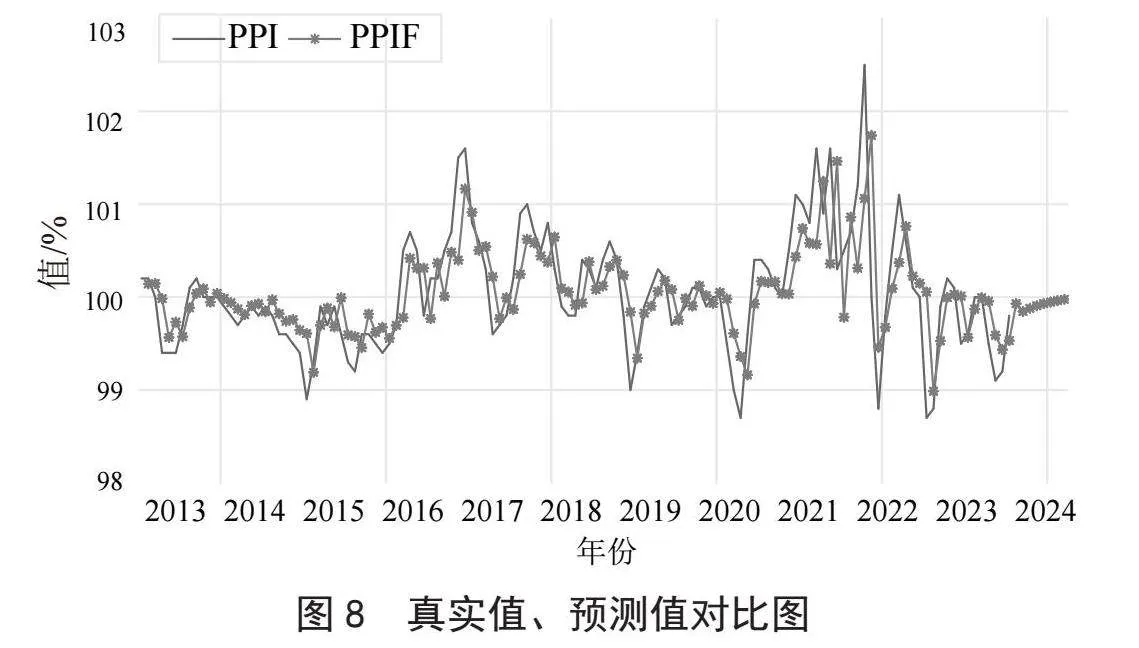
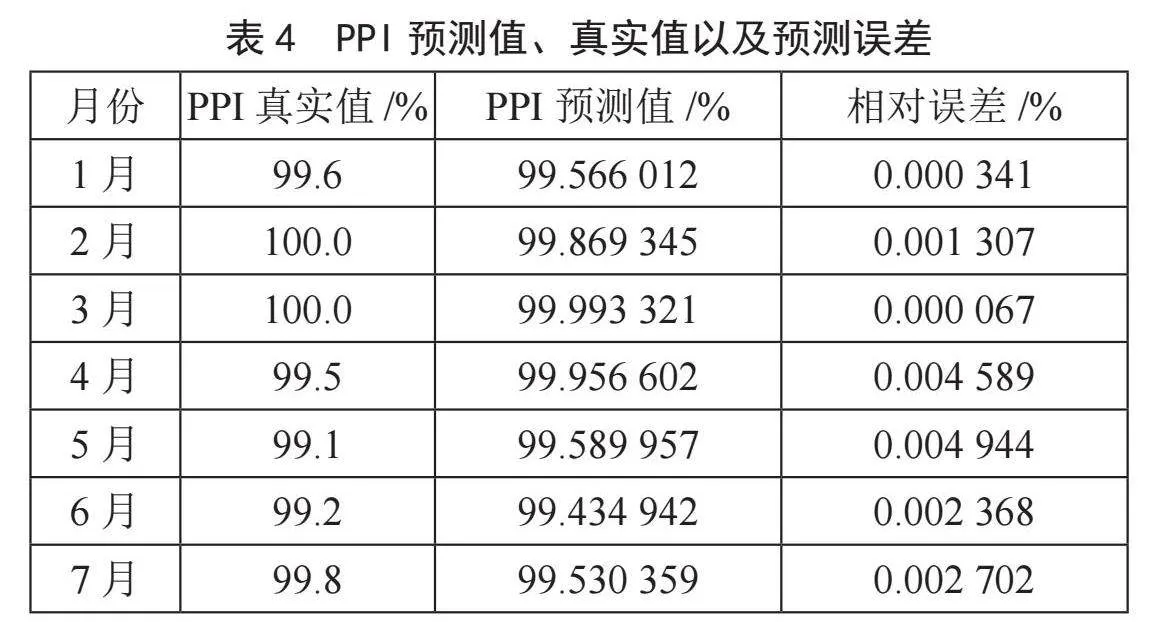
如图8和表4所示,在样本内静态预测图中,将我国2023年1月至7月的PPI预测值与实际值进行对比,可以看出模型的预测精度较好。
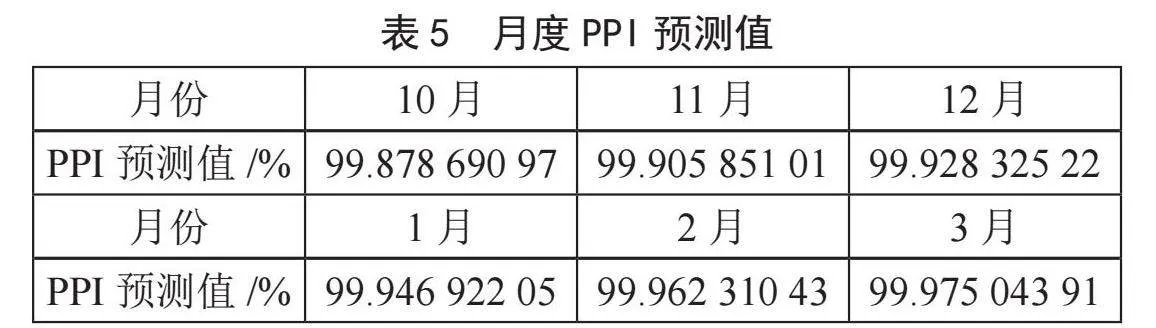
随后,我们对模型进行样本外动态预测分析,以评估模型的预测能力。预测时间范围2023年10月至2024年3月,如表5所示。
针对我国2013年1月至2023年7月间的PPI数据,我们建立ARIMA(1,0,2)模型。通过上述分析,我们可以看出该模型对PPI数据的变化趋势进行了较好的拟合,与实际数据基本一致。这表明该模型对生产者价格指数的短期预测具有较高的准确性,对研究PPI具有重要的意义。
3 结 论
通过分析和预测表明:我国生产者价格指数在2023年未来6个月内基本走势比较稳定,波动幅度缓和。我认为可以采取以下措施来抑制PPI过快上涨:首先,加强对工业品出厂价格的监管,限制工业品出厂价格的过快上涨,防止PPI的快速攀升;其次,加强对市场供需情况的调查研究,并及时发布相关数据,避免供需失衡导致PPI上涨;再者,加大对涨价行为的处罚力度,严厉打击价格垄断和恶意涨价行为,维护市场秩序,稳定PPI;最后,加强货币政策的调控,保持货币政策的稳定性,避免通货膨胀对PPI的过快上涨。通过以上措施的综合施行,可以有效抑制PPI的过快上涨,维护市场稳定。此外,可以充分利用大额外汇储备的作用。一方面,可以通过增加外汇储备来购买一定数量的能源和重要原材料,以稳定市场价格;另一方面,可以通过调配部分外汇储备,为能源和重要原材料进口企业提供补贴,以减轻它们的生产成本。这些措施的综合施行可以有效应对PPI过快上涨的情况,维护市场稳定。
参考文献:
[1] 杨业伟,许宪春.PPI与CPI的传导效应分析 [J].统计与决策,2022,38(13):62-66.
[2] 伊力扎提·艾热提.中国消费者价格指数预测模型的选择 [J].统计与决策,2022,38(4):68-73.
[3] 司圃旭.基于变量选择和ARIMAX模型的山东省GDP预测 [D].济南:山东大学,2019.
[4] 李志超,刘升.基于ARIMA模型、灰色模型和回归模型的预测比较 [J].统计与决策,2019,35(23):38-41.
[5] 王鄂,张霆.时间序列在湖南省GDP预测中的应用——基于ARIMA模型 [J].青岛大学学报:自然科学版,2019,32(3):136-140.
[6] 王立柱.基于计算智能的时间序列模型及预测研究 [D].大连:大连理工大学,2015.
[7] XU D H,ZHANG Q,DING Y,et al. Application of a Hybrid ARIMA-LSTM Model Based on the SPEI for Drought Forecasting [J].Environmental Science and Pollution Research,2021,29(3):4128-4144.
[8] 严彦文.基于ARIMA模型的山东省GDP的分析与预测 [J].数学的实践与认识,2018,48(4):285-292.
[9] TANDON H,RANJAN P,CHAKRABORTY T,et al. Coronavirus (COVID-19): ARIMA-based Time-series Analysis to Forecast near Future and the Effect of School Reopening in India [J].Journal of Health Management,2022,24(3):373-388.
[10] 孙颖.基于ARIMA模型的消费者价格指数预测 [J].统计与决策,2016(11):83-85.
作者简介:陶永(1999.03—),女,黎族,贵州普安人,硕士研究生在读,研究方向:统计模型。