

摘" 要:揭棋是中国象棋的一个变种玩法,相较于中国象棋策略、收益皆透明的模式,揭棋无法确定收益和后续策略,属于非完全信息博弈,需要开发新的算法才能实现揭棋人机对弈。文章设计并实现了基于Alpha-beta剪枝技术辅以启发式搜索的揭棋程序,通过创造极大层与极小层之间的暗子扩张层构建出适合揭棋使用的博弈树结构,基于中国象棋的分值评价标准设计了适用于揭棋的评分体系,解决了对暗子的评分与深层搜索问题,实现了对揭棋状态复杂度与揭棋算法的初步探索。
关键词:非完全信息博弈;Alpha-beta剪枝;揭棋;中国象棋
中图分类号:TP301.6 文献标识码:A 文章编号:2096-4706(2024)18-0048-05
Design and Implementation of Revealed Chess Algorithm Based on Alpha-beta Pruning Tree
LIU Fengrui, TIAN Shaojie, REN Yuxin
(Computer School, Beijing Information Science and Technology University, Beijing" 100101, China)
Abstract: Revealed chess is a Chinese chess variant, and compared with the pattern of Chinese chess, where strategies and profits are transparent, revealed chess cannot determine profits and subsequent strategies, and belongs to incomplete information game, which requires the development of a new algorithm to enable a revealed chess man-machine game. This paper designs and implements a revealed chess program based on Alpha-beta pruning technology supplemented by heuristic searching to construct a game tree structure suitable for revealed chess by creating a dark matter expansion layer between the maximal layer and the minimal layer. And it designs a scoring system suitable for revealed chess based on the scoring standard of Chinese chess, which solves the problems of scoring dark matter and deep search, and realizes the initial exploration of the complexity of revealed chess state and revealed chess algorithm.
Keywords: incomplete information game; Alpha-beta pruning; revealed chess; Chinese chess
0" 引" 言
完全信息博弈的棋类如国际象棋、围棋、中国象棋等在机器博弈领域已经被研究得相当透彻,几乎做到了拥有战胜顶尖职业棋手的水平。而非完全信息博弈的机器博弈项目大多属于牌类或是与牌类原理类似的幻影围棋、军棋等棋类,这些博弈中的未知信息是对手采取的策略,是单向不透明的。揭棋是中国象棋的变种玩法之一,同时也是一种非完全信息博弈棋类,双方采取的策略完全透明,但收益却双向不透明。
这种博弈模式非常少见,它并非Harsanyi定义的the Harsanyi transformation中拥有私人信息的情况[1],而是双方都只知道某个先验概率却无法确定最终的收益。这种机制独特,问题复杂度较高的博弈类型是值得研究的。
在过去的几十年中,有很多适用于棋类的算法被研究出来。其中较为常用的有极大极小搜索[2]、Alpha-beta剪枝[3]、Zobrist哈希算法[4]等。
本文将会讨论一种基于Alpha-beta剪枝算法与贝叶斯公式原理[5]的揭棋算法设计方式以及该算法对应的评分标准,为后续的揭棋研究工作提供启发与帮助作用。
1" 揭棋规则
1.1" 棋子摆布与胜负判定
中国象棋棋盘9条竖线,10条横线,总计90个位置[6]。棋子有红黑两种颜色,每方16枚棋子,分别是:车、马、炮、相、士、将、卒这7种。
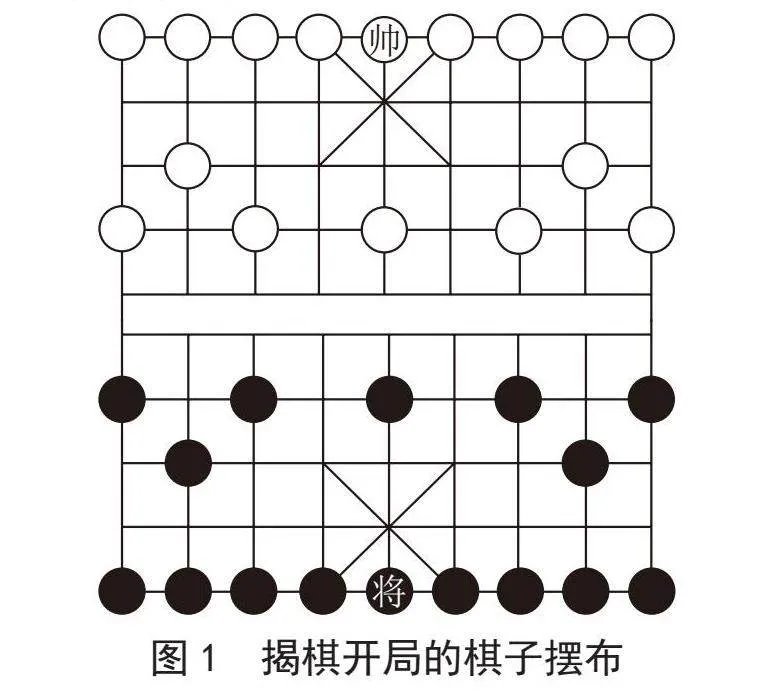
揭棋的胜负判定遵循中国象棋的胜负判定规则[7]。同时,揭棋的棋盘与棋子摆布也与中国象棋的摆法相同,只不过除“将”“帅”外的棋子需要翻面变为暗子并随机摆放到某个棋子的初始位置上。开局时的棋子摆放如图1所示。
1.2" 棋子走法
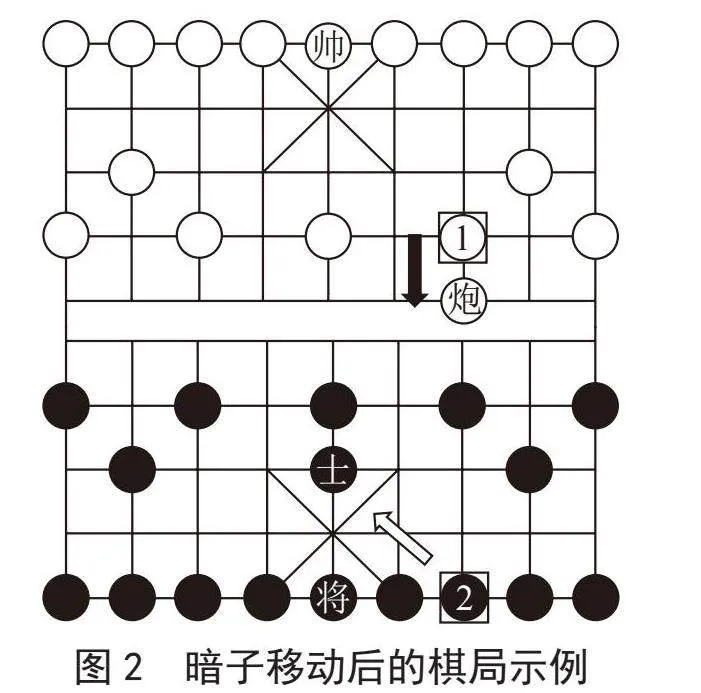
暗子的走法与其位置有关,该子在中国象棋中哪个棋子的位置上,那么暗子就要按照这个棋子的走法来行棋,暗子走过一步后需要翻面变成明子。暗子移动后的棋局如图2所示,在该图中,白棋“兵”位置上的暗子1按照“兵”的走法向前进一步,翻开后明子为“炮”,威胁到了黑棋“象”位置上的暗子2,于是黑棋以“象”的走法移动该暗子,翻开后明子为“士”。
揭棋的明子共有“车”“马”“炮”“象”“士”“卒”六种,明子的走法与中国象棋中的棋子走法基本一致,其中略有变化的是:
1)“士”一次只能走一个斜格,并且可以过河。
2)“象”的走法是每次循对角线走两格,俗称“象飞田”。如果它走的“田”字中央有一个棋子,就不能走,俗称“塞象眼”[8],同时“象”也可以过河。
3)其余明子的走法与中国象棋中的棋子走法一致[8]。
2" 算法设计
2.1" Alpha-beta剪枝原理
Alpha-beta剪枝树是在极大极小搜索算法的基础上进行改进的。极大极小搜索模拟的是两个人和博弈中双方的交替选择行为:在搜索的过程中,假定每一方都选择对自己最有利的行动,从单方角度看就是一次取最大值、一次取最小值的过程[2]。这一过程可以用交替取极大值与极小值的搜索树来表示。
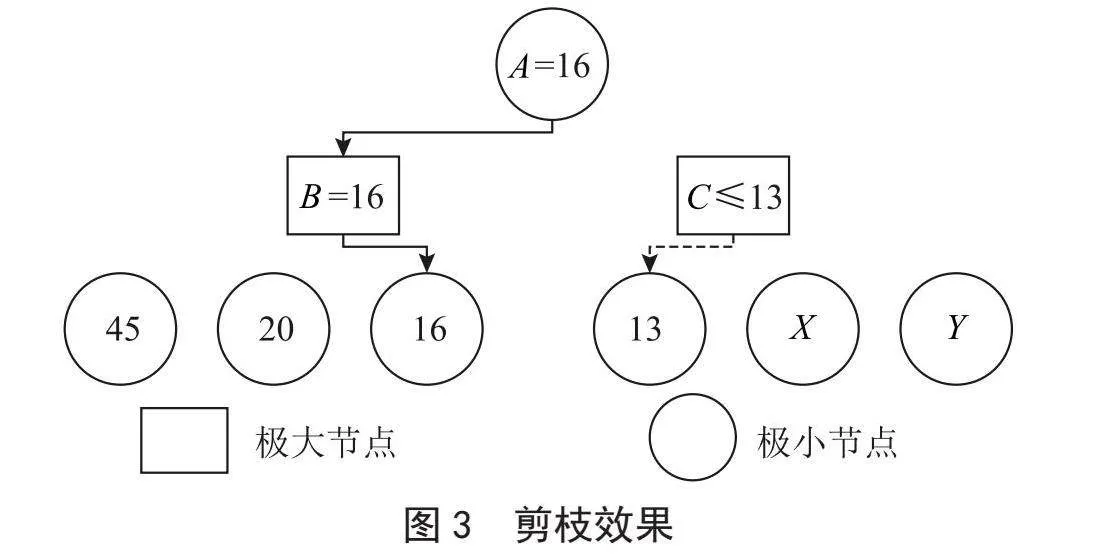
Alpha-beta剪枝是对极大极小搜索算法的一种改进。由于搜索树是从左到右遍历的,当在max层已经搜索得到一个分支的值,如果另一分支的最大值必然小于该值,那么就不需要继续搜索那个分支了[3]。如图3所示,假定A是这棵搜索树的父节点,它应该在极大层的两个节点B、C中选择一个节点的值作为A节点自身的值。由于该树是递归调用产生的,所以B节点的值会被优先搜索。B节点的子节点是极小节点,应该从三个子节点中选出最小值16作为B节点的值。接下来需要得到C节点的值来与B节点进行比较。C节点的子节点也是极小节点,搜索到的第一个子节点的值是13,由于C节点要取三个子节点中的最小值,那么C节点的取值必然小于等于13,因此B节点的值就一定大于C节点。无须继续搜索,将B节点的值返回给A节点即可,那么最终得到A节点的值是16,这个过程可以由以下公式来表示:
Value(A)=max(16,min(13,X,Y))
其中Value函数为输入节点的取值,max函数为从输入的几个节点中取最大值,min函数为从输入的几个节点中取最小值,X、Y为C节点的另外两个子节点的值,其值可以为任意实数。
通过Alpha-beta剪枝,再辅以合适的启发式搜索算法,搜索树的效率可以得到大幅提升,足够揭棋使用了。
2.2" 揭棋的博弈树结构设计
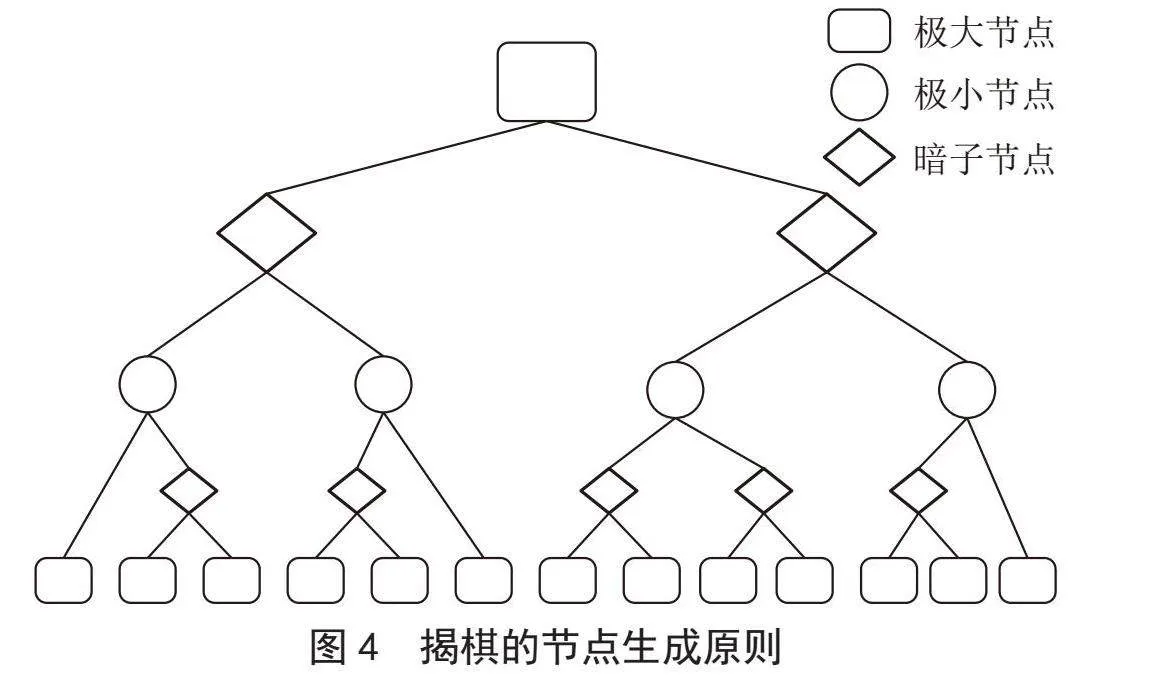
由揭棋的规则可以发现,揭棋不同于普通中国象棋博弈树中一种走法生成一个节点的形式。由于暗子翻面后有多种的可能性,翻面后的每种可能性都应当放到博弈树中进行模拟,这就使得我们不能用传统的构建方式去构建这棵博弈树。
暗子与正常棋子的区别是在翻面后才产生的,因此只需要在生成暗子走法后对博弈树的结构进行修改即可。在暗子的走法生成后,我们可以将暗子移到新的位置并且做出标记。调用暗子模拟的函数,该函数会找到棋盘中被标记的暗子,并且将该暗子分别修改成各个可能出现的明子,把不同的翻面结果依次传递给递归函数,继续向深处搜索。最后的分值依照贝叶斯公式由概率算出相应的加权平均数即可,其中的概率计算方式如该公式所示:
P=Nt /Nm
其中P为该情况发生的概率,Nt为这种棋子还剩几个没有被翻开,Nm为总共还有几个明子没出现在棋盘上。最后生成的树结构就如图4所示。
由图4可以看出,揭棋的广度扩张速度是大于中国象棋的。明子共有六种、十五颗,在暗子数量较多的情况下,同层节点数在经过暗子节点扩张后大致会增加四到五倍,更深层的节点数更是会指数级增加。因此在代码的具体实现时,根据暗子的数量改变搜索的广度、深度是十分重要的。
2.3" 棋子分值设计
对于揭棋来说,大多数子力的价值都可以挪用中国象棋的评价标准[9-10],只有“卒”“象”“士”和暗子的评价标准需要重新设计。
棋子的分值应该从位置价值和子力价值两个维度考虑。其计算公式如以下公式所示:
score=scorep+scorec
其中score为棋子的实际分值,scorep为位置价值,scorec为子力价值。
2.3.1" 暗子分值设计
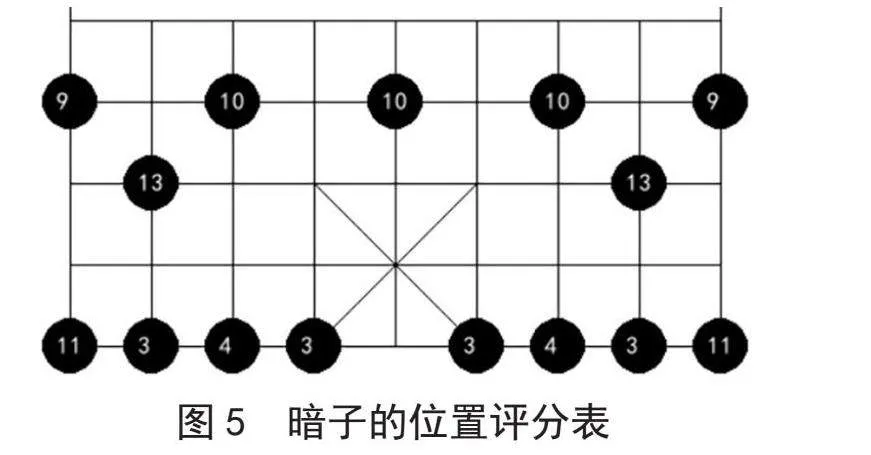
1)位置价值。暗子的位置价值由灵活度和可走位置决定。灵活度、可走位置不好的棋子,评分就相对低一些。具体的分值如图5所示,其中,五个“卒”位置上的暗子能够达到的位置都是河界旁边的位置,对所有棋子来说都是比较好的位置,因此“卒”位置暗子的评分是9~10分,越靠中间位置的暗子评分就相对高一些。“炮”位置的暗子是唯一开局就能越过河界的棋子,灵活度最高,因此分数是最高的13分。“车”位置的暗子保护底线能力强,在没有阻碍的情况下灵活度也不错,因此分数为11分。“马”“象”“士”位置的暗子活动能力差,甚至可能会在移动后堵塞九宫格,评分只有3~4分。
2)子力价值。暗子的子力价值由尚未翻开的棋子确定。尚未翻开的棋子的子力平均值就是该暗子的实际子力价值。最后将子力价值与位置价值相加就得到了暗子的分数。
2.3.2" 棋子“象”分值设计
1)位置价值。在揭棋中“象”可以过河并且初始位置不固定,所以需要给棋盘上每个点都设置一个对应的“象”的位置分值。位置分值的设计原则为:过河前分值较低、过河后位置较高;所有可能达到的位置中如果有敌方九宫格的,该系列“象”位的所有评分适当升高;当前位置下一步可选位置较多的适当提高分数,具体的评分如图6所示。
2)子力价值。由于揭棋中“象”形成连环的概率大大降低,防守属性骤降。加上其可走点位少,进攻能力同样很差,所以“象”的子力价值相比中国象棋的评分标准要相对降低,本程序给定的分值为15分。
2.3.3" 棋子“士”分值设计
1)位置价值。“士”与“卒”类似,未过河时评分低,位置越靠后评分越低,靠近我方九宫格后评分相对高,过河后评分大幅提升,越靠近对方九宫格评分越高。由于“士”可以后退,所以不会像“卒”一样下底后评分骤降,具体的评分如图7所示。
2)子力价值。形成连环“士”的成本通常很高,防守属性弱化,但能过河加强了“士”的进攻能力,综合来看子力价值与中国象棋中的“士”相近,本程序中给定的分值为20分。
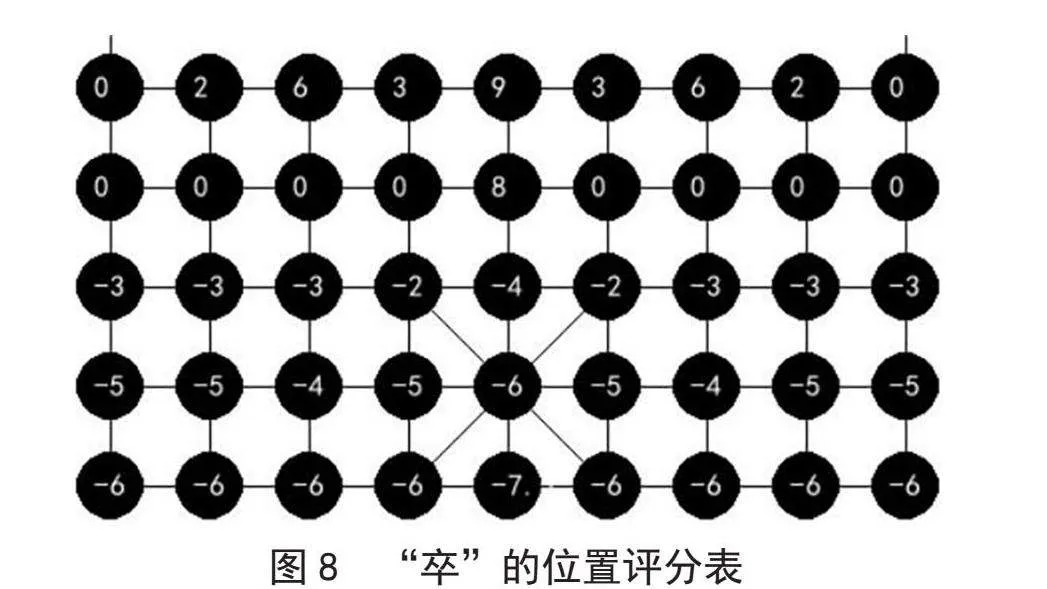
2.3.4" 棋子“卒”分值设计
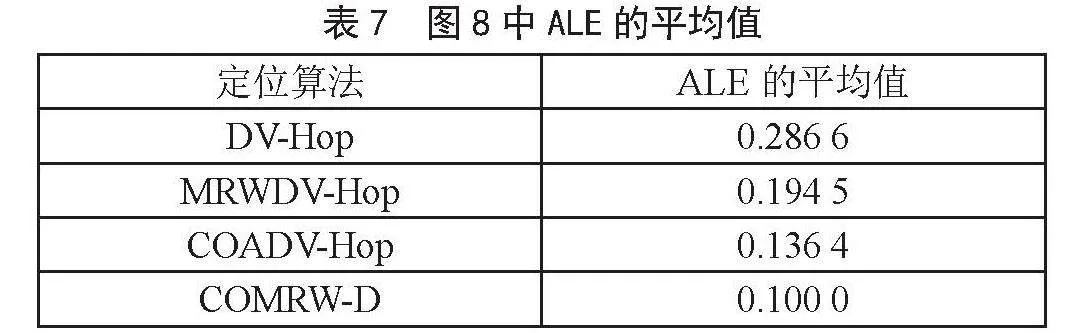
1)位置价值。未过河前,位置越靠后评分越低,在九宫格内的评分要相对更低一些,过河后与中国象棋评分标准一致,过河前的具体的评分如图8所示。
2)子力价值。与中国象棋相比没有明显变化,本程序中给定的分值为7分。
2.4" 效率优化
由于暗子导致的广度大幅增加情况,本程序选择在暗子少于12个时搜索六层深度,否则搜索四层深度,这样可以减少搜索的节点数量,提高系统运行效率。由于暗子多的情况下实际上难以对预期收益进行准确衡量,因此深度的减少并不会对性能有较大影响。
添加了Zobrist原理的开局库,通过hash搜索能够在短时间内找到所存储局面的最佳走法。同时,本程序添加了贪心搜索和空招搜索[6]作为启发式搜索,以此减小搜索的广度。
其中贪心搜索就是利用贪心算法的思想只搜索局部最佳着法,并只将贪心搜索中得分较高的节点放入博弈树中模拟,有效减小了搜索广度。
而空招搜索则会让对方连续走两步,如果让对方连续走两步后我方对局面的评分高于对方走一步时的评分,这就证明对方暂时没有能够有效杀伤我方棋子的手段,该分支就不必继续搜索。
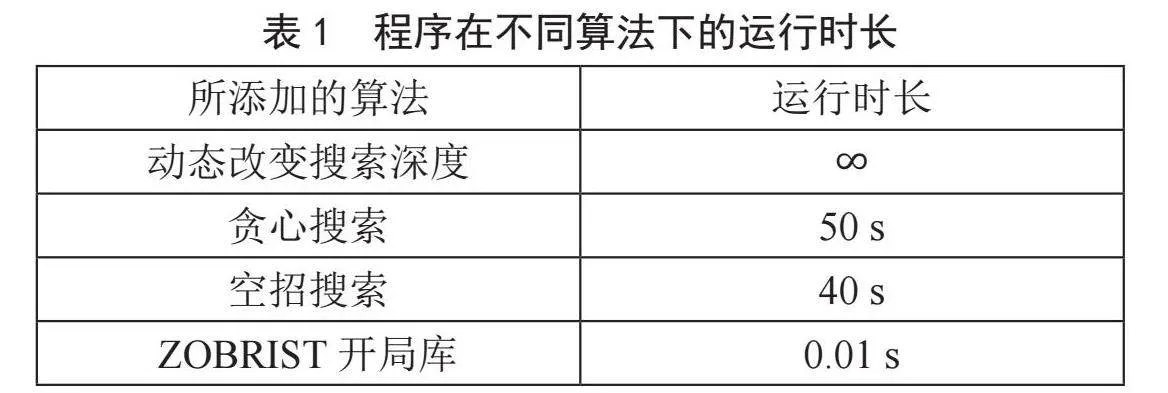
揭棋的开局实际上是博弈树搜索广度最广的情况,因此接下来会用本程序计算第一步时所花的时长为例,简单对比各种算法对程序的优化效果。需要注意的是,该数据仅代表程序在用来实验的这台计算机上运行的时间,并不能代表所有情况。具体数据如表1所示,在该表中,每一种算法的运算时间实际上都是基于前项所有算法的基础上的。
3" 结" 论
本文利用暗子节点作为极大层与极小层之间的中间节点,解决了揭棋中暗子后续局面无法深层模拟的问题。又基于传统中国象棋评价标准设计了揭棋中暗子与部分明子的分值与位置评分表。最终基于以上成果初步实现了一个揭棋的人机对弈程序,该程序添加了悔棋、交换先后手、重新开始等对弈中的必要功能。经过测试,该程序对局势优劣有基本的判断,通常能够走出合理着法,有概率可以战胜业余爱好者。由于揭棋的随机性较强,且人类棋手水平难以量化,该结果仅供参考。
由于水平有限,本程序的棋力和效率仍有较大提升空间。
棋力方面,可以考虑通过添加平静搜索、将军延伸等启发式搜索算法,可以有效提高算法搜索的准确率,提高棋力。通过自适应遗传算法确定一份更适用于揭棋的评分标准也能提升AI对局面判断的准确性。同时也可以将剪枝树与蒙特卡洛算法或B*算法结合,算法的棋力也会有相应的提升,或者直接设计基于神经网络技术的揭棋程序,搜索的准确度会更高。效率方面,可以重构走法生成部分,或者将部分代码更好地封装减少重复调用,也可以考虑利用并发技术提升运算效率。
参考文献:
[1] HARSANYI J C. Games with Incomplete Information Played by“Bayesian”Players Part II. Bayesian Equilibrium Points [J].Management Science,1968,14(5):320-334.
[2] SHANNON C E. Programming a Computer for Playing Chess [J].Philosophical Magazine,1950,41(314):256-275.
[3] KNUTH D E,MOORE R W. An Analysis of Alpha-beta Pruning [J].Artificial Intelligence,1975,6(4):293-326.
[4] ZOBRIST A. A New Hashing Method with Application for Game Playing [J].ICCA Journal,1990,13(2):69-73.
[5] BAYES T. An Essay Towards Solving a Problem in the Doctrine of Chances [J].Philosophical Transactions of the Royal Society of London,1764,53:37-418.
[6] 黄晨.棋类游戏中的先行权 [J].智能系统学报,2007(3):91-94.
[7] 中国人工智能学会机器博弈专业委员会.亚洲象棋规则 [EB/OL].[2023-10-06].http://computergames.caai.cn/jsgz11.html.
[8] 百度百科.中国象棋 [EB/OL].[2023-10-06].https://baike.baidu.com/item/%E4%B8%AD%E5%9B%BD%E8%B1%A1%E6%A3%8B/278314.
[9] 徐心和,王骄.中国象棋计算机博弈关键技术分析 [J].小型微型计算机系统,2006(6):961-969.
[10] 王骄,王涛,罗艳红,等.中国象棋计算机博弈系统评估函数的自适应遗传算法实现[J].东北大学学报,2005,126(10):949-952.
作者简介:刘丰瑞(2003—),男,满族,辽宁丹东人,本科在读,研究方向:棋类机器博弈、状态复杂度问题;田少杰(2002—),男,土家族,贵州思南人,本科在读,研究方向:前端设计;任玉昕(2001—),男,汉族,北京人,本科在读,研究方向:软件工程。