摘 要:军民通用装备动员作为装备动员的重要组成部分,是战时弥补保障装备不足的快捷手段之一。而供应企业作为军民通用装备动员潜力的核心载体,开展等级评估研究,对动员资源选择的决策具有重要支撑作用。以往对企业评估问题的研究中,解决方法普遍流程复杂、定性因素多、人为干预多,不适用于常态化开展多领域动员企业评估。文章基于现行动员潜力统计指标体系下,探索利用降维处理后聚类分析方法,构建军民通用装备动员企业等级评估模型,并通过实验分析验证其适用性及实用性。
关键词:军民通用装备动员;降维算法;聚类算法
中图分类号:TP391 文献标识码:A 文章编号:2096-4706(2024)20-0123-06
Research on Grade Evaluation of Civil-military Dual Use Equipment Mobilization Supply Enterprises Based on Clustering Algorithm
YUCHI Jingwei, LING Haifeng, CHU Detian, KANG Wei
(Army Engineering University of PLA, Nanjing 210007, China)
Abstract: As an important part of equipment mobilization, civil-military dual use equipment mobilization is one of the quick means to make up for the shortage of support equipment in wartime. As the core carrier of mobilization potential of civil-military dual use equipment, the research on grade evaluation of supply enterprises has an important supporting role in the decision of mobilization resource selection. In the previous research on enterprise evaluation problems, the solutions generally has complicated process, many qualitative factors, and many human interventions, which are not suitable for the regular implementation of multi-field enterprise evaluation. Based on the current mobilization potential statistical index system, this paper explores the use of cluster analysis method after dimensionality reduction to build a civil-military dual use equipment mobilization supply enterprise grade evaluation model, and verifies its applicability and practicability through experimental analysis.
Keywords: civil-military dual use equipment mobilization; dimensionality reduction algorithm; clustering algorithm
0 引 言
现代战争节奏快,装备资源消耗量大,装备动员能力建设在国防动员建设中具有重要的地位。军民通用装备动员作为装备动员的重要组成部分,具有潜力资源丰富、动员成本低廉、部署高效便捷的特点,是战时弥补保障装备不足的快捷手段之一,也是地方支援军队的最直接形式之一。
军民通用装备资源的核心载体,是涉及各行各业的地方企业。进行企业等级评估,是动员潜力分析的一项重要内容,可准确掌握辖区内各类军民通用装备的供应水平,为产业结构调整、优化资源配置提供依据;通过良好的反馈机制,可激励企业改进其业务流程、提高产品质量和服务水平;同时,也是强化应急准备能力的重要支撑,根据企业分级情况可构建动员梯队,确定某行业领域企业动员优先级,据此提升动员预案的计划性、科学性,为紧急情况下实现快速动员提供保障。
1 军民通用装备动员企业等级评估问题分析
1.1 研究现状及研究目的
以往研究中,普遍采用的企业评估方法大多如下:首先结合法规依据及深入调研,构建复杂的指标体系,包括定量指标和定性指标,定性指标一般还需通过专家评价法进行确定;而后选取适当的数据分析方法,构建数学模型;实际应用时,将根据指标体系梳理形成的企业数据带入模型进行计算,从而得到评估结果。
上述方法对于具体某类企业或者企业某项具体能力进行评估,是较为全面且科学的。但动员企业评估问题,是在动员准备阶段,即平时状态下对各领域企业进行的一种例行性、常态化的评估,企业类型众多,使用此类方法解决过于复杂,工作量较大,效率不高。本文旨在基于现潜力统计指标体系下,探索一种快速、高效且兼顾科学性的分析方法,以此提高动员企业评估质效。
1.2 问题分析及解决方法
军民通用装备动员企业的等级评估,目标不在于根据提前划定的等级标准,来确定每个企业归属情况。而是将现有企业集合,根据内部比较的优劣情况,划分企业间的优先级。
聚类分析法是一种在数值统计分析领域中广泛应用的多元统计分析方法,它能在不知道类型的个数或对于各种类型的结构未做任何假设情况下,将一批样本数据进行自动归类。通过这种方法,可以将样本分为若干个具有共性的群体,同时确保群体间具有明显的差异性[1]。聚类过程本身不依赖于预先设定的分类准则,而是直接根据样本的变量特征来客观地界定分类的标准,这种特性能很好适应军民通用装备动员企业等级评估的需求。因此,我们可以将原问题转化为聚类分析问题。
在面对大量评估指标时,直接进行聚类分析较为复杂,并且不同指标之间可能存在高度的信息冗余和相关性,容易对分析结果造成干扰。为了解决这一问题,可以采用降维方法,将众多具有相关性的原始指标转化为一组数量较少的综合指标。每个新指标是原始指标的线性组合,能够捕捉原始数据集的大部分关键信息,并且新指标之间互不相关[2]。
综上,我们可以将军民通用装备供应企业等级评估问题映射为降维处理后的聚类分析问题进行解决。
2 算法分析
当前军民通用装备供应企业潜力数据信息具有多属性、各属性量度不一致等特征。对数据进行预处理后,采用不同降维方法进行数据降维,而后基于K-means聚类算法对军民通用装备供应企业数据进行聚类分析,并根据聚类结果选用合适的聚类方法,最后实现动员企业的等级评估。
2.1 主成分分析法
主成分分析法(Principal Component Analysis, PCA)通过正交变换将一组可能相关的变量转换成一组线性不相关的变量,这组新的变量被称为主成分。PCA的主要目的是数据降维,即减少数据集的维度,同时尽可能保留原始数据的重要信息[3]。原理步骤如下:
1)标准化数据。由于PCA对数据的尺度敏感,因此在应用PCA之前,通常需要对数据进行标准化处理,使每个特征的均值为0,标准差为1。
2)计算协方差矩阵。协方差矩阵描述了数据集中各个变量之间的线性关系。协方差矩阵的特征值和特征向量是PCA的核心。
3)求解特征值和特征向量。对协方差矩阵进行特征分解,得到一系列的特征值和对应的特征向量。特征值表示了每个特征向量方向上的数据方差。
4)选择主成分。根据特征值的大小对特征向量进行排序,特征值越大,对应的特征向量方向上的数据方差越大,因此越重要。选择前k个最大的特征值对应的特征向量作为主成分。
5)构造新的特征空间:将原始数据投影到选定的主成分上,形成新的特征空间,这些新的特征是原始数据的线性组合,且彼此正交(线性无关)。
2.2 统一流形逼近与投影技术
统一流形逼近与投影(Uniform Manifold Approximation and Projection, UMAP)是一种相对较新的非线性降维技术,其目的是将高维数据集映射到低维空间,同时尽可能保留数据的全局结构和局部结构。因此,UMAP特别适合于数据可视化和探索性数据分析。原理步骤如下:
1)构建高维图表示。UMAP首先在高维空间中构建数据的图表示,这个图是一个模糊单纯复形,其中边的权重表示数据点之间的连接可能性。UMAP通过从每个点向外扩展一个半径(称为带宽或距离)来确定这些连接,当半径重叠时,点之间就建立了连接。
2)选择带宽。带宽的选择对UMAP的结果至关重要。太小的带宽可能导致过度细分的集群,而太大的带宽可能导致所有点都连接在一起。UMAP通过考虑每个点的第n个最近邻的距离来选择局部带宽,从而在局部结构和全局结构之间取得平衡。
3)优化低维布局。一旦高维图表示构建完成,UMAP将使用一种特殊的优化过程来寻找一个低维布局,使得低维空间中的点尽可能地反映高维图中的拓扑结构[4]。
2.3 K-means算法
K-means是一种广泛使用的聚类算法,它的目标是将数据点划分为K个簇,使得每个点与其所属簇的中心之间的距离之和最小。这种算法是基于距离的聚类方法,特别适用于解决划分问题。原理步骤如下:
1)初始化。随机选择K个数据点作为初始的簇中心。
2)分配步骤。将每个数据点分配给最近的簇中心,即根据数据点与各簇中心的距离来确定其所属的簇。
3)更新步骤。重新计算每个簇的中心,通常是取簇内所有点的均值作为新的簇中心。
4)迭代。重复分配和更新步骤,直到满足停止条件(例如,簇中心的变化小于某个阈值,或者达到预设的迭代次数)。
5)收敛。当簇中心不再发生变化,或者变化非常小,算法停止迭代,此时认为K-means已经收敛[5]。
2.4 聚类效果评估方法
2.4.1 可视化方法
聚类结果的可视化评估是通过图形化的方式对聚类算法的效果进行定性分析的方法。本文我们使用散点图进行可视化评估。每个数据点的位置由其特征值确定,不同簇的数据点使用不同的颜色或形状,我们通过观察簇的分离性和紧凑型,来直观反映出评估结果的好坏。理想情况下,同一簇的点应该紧密地聚集在一起,而不同簇之间有明显的间隔。如果某些簇的数据点分散在图中,这可能表明聚类效果不佳。
2.4.2 指标评估
本文选择聚类算法常用的轮廓系数(Silhouette Coefficient, SC)[6]、Calinski-Harabasz指数(Calinski-Harabasz Index, CHI)[7]、戴维斯-邦丁指数(Davies-Bouldin Index, DBI)[8]三种指标作为评估依据。
1)轮廓系数。轮廓系数结合了聚类的凝聚度和分离度。对于每个数据点 轮廓系数SCi定义为
(1)
其中ai为点i与同簇其他点的平均距离(簇内距离),bi为点i与最近簇的所有点的平均距离(簇间距离)。轮廓系数的值范围在-1到1之间:接近1表示点i与同簇点非常接近,与不同簇的点非常远离,即凝聚度高且分离度好;接近-1表示点i被错误地分配到了簇中;接近0表示点i在两个簇的边界上。所有点的轮廓系数平均值,即该聚类结果的总轮廓系数。
2)Calinski-Harabasz指数。Calinski-Harabasz指数也称为方差比率准则,它是簇间离散度与簇内离散度的比值。对于k个簇,CHI定义为:
(2)
其中,Bk为簇间散布矩阵,Wk为簇内散布矩阵。Trace为矩阵迹的和,即矩阵对角线元素的和。CHI值域为正数,没有理论上的上限,值越大,表示簇间差异越大且簇内差异越小,聚类效果越好。
3)戴维斯-邦丁指数。DBI是一种基于簇内相似性和簇间不相似性的评估指标。对于任意两个簇i和j,DBI定义为:
(3)
其中,Si为簇i的簇内相似性,dij为簇i和簇j之间的距离,dii和djj分别为簇i和簇j簇内距离。DBI值域是正数,没有理论上的上限,当DBI指数接近0时,表示簇之间的分离度很好,即不同簇的数据点之间的相似性很低,聚类效果越好。
3 评估模型构建
3.1 指标体系确定
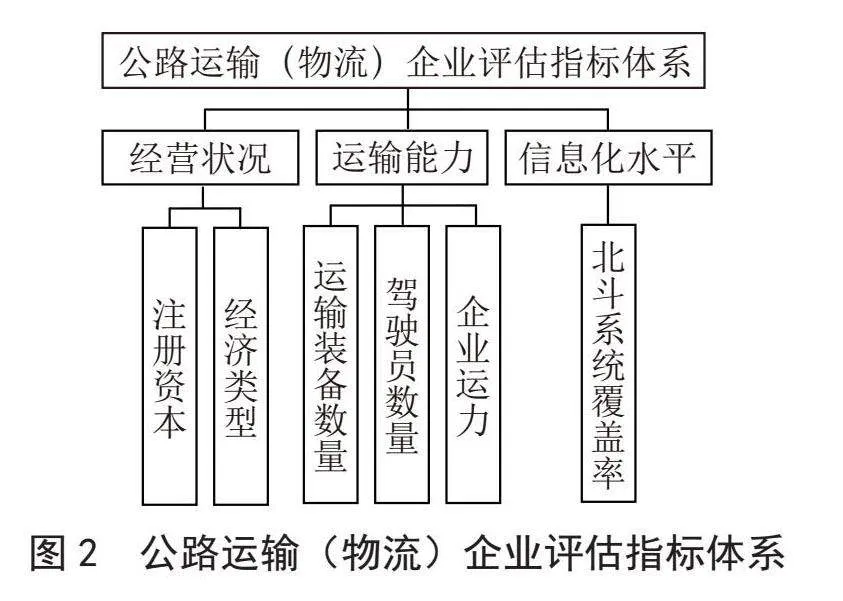
现行动员潜力统计中,涉及各具体行业领域的军民通用装备供应企业信息采集表,如《大型工程机械所属(生产制造销售)企业采集表》《航空器修造企业采集表》等,其中已包括较为全面的指标要素,分析人员还可根据现实情况采用潜力统计中其他相关结果继续扩充评估指标。如《公路运输(物流)企业采集表》中,已有企业经济类型、驾驶员数量、企业运力等多个指标要素,我们还可以结合其他潜力数据表中的企业注册资本、运输车辆数量、北斗系统配置情况进行指标扩充。据此,我们可基于已有潜力统计指标体系快速抽组企业等级评估指标体系。
3.2 数据预处理
指标体系确定并梳理构成数据集后,由于部分指标为非数据型指标,需进行赋值处理以便后续算法分析。如针对“经济类型”指标,原始类别区分“国有全资”“国有控股”“民营”等,那么根据实际优选逻辑,我们可以给“国有全资”赋最高分值3,给“国有控股”赋中间分值2,给“民营”赋最低值1。
3.3 算法分析并取最优解
由于不同降维方法后聚类的效果会有差异,根据择优思维,分析过程我们采用两种常用降维方法,即PCA和UMAP,并将两种降维处理后的数据运用K-means算法,进行3至6簇的聚类分析。根据聚类效果评估方法,对比不同降维方法及不同簇数下的聚类效果,选取最优解。
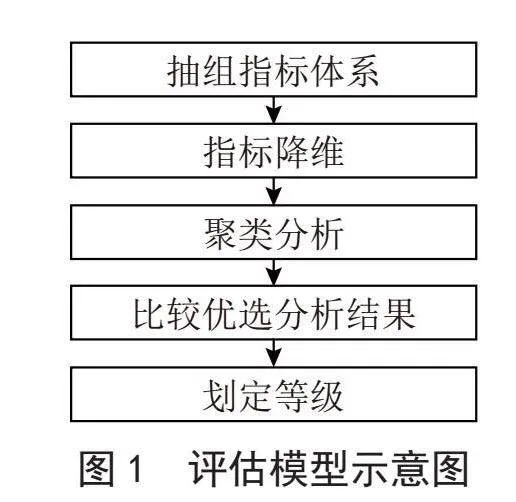
3.4 结果分析
根据最优聚类结果,回归原始指标数据进行分析,即分析聚类后各类企业的指标数据特征,根据现实需要,将各企业集合进行等级划分,评估模型如图1所示。
4 实验分析
以公路运输(物流)企业为例,进行企业等级评估,以验证本研究方法的可行性和有效性。
4.1 数据来源
从某地级市潜力数据库中,随机抽取31家和665家公路运输(物流)企业数据,分别作为小、大数据样本进行对比实验。
4.2 实验方法
首先结合潜力数据指标体系确定企业评估的具体指标,然后采用PCA-Cluster、UMAP-Cluster两种降维处理后的聚类方法先对小样本数据进行分析,再用同样模式对大样本数据进行分析,根据分析结果讨论本方法对于大、小样本数据的适用性。并根据最优聚类结果对企业进行等级划分。
4.3 评估指标确定
以现行国家物流企业分类与评估指标为参考[9],综合分析物流企业参与军事行动运输任务的应考虑的相关因素[10],立足现行国防动员潜力调查统计指标体系,抽取确定企业评估指标体系。
评估指标分为经营状况、运输能力、信息化水平3个一级指标,注册资本、经济类型、运输装备数量、驾驶员数量、企业运力、北斗系统覆盖率6个二级指标,如图2所示。
4.4 实验结果
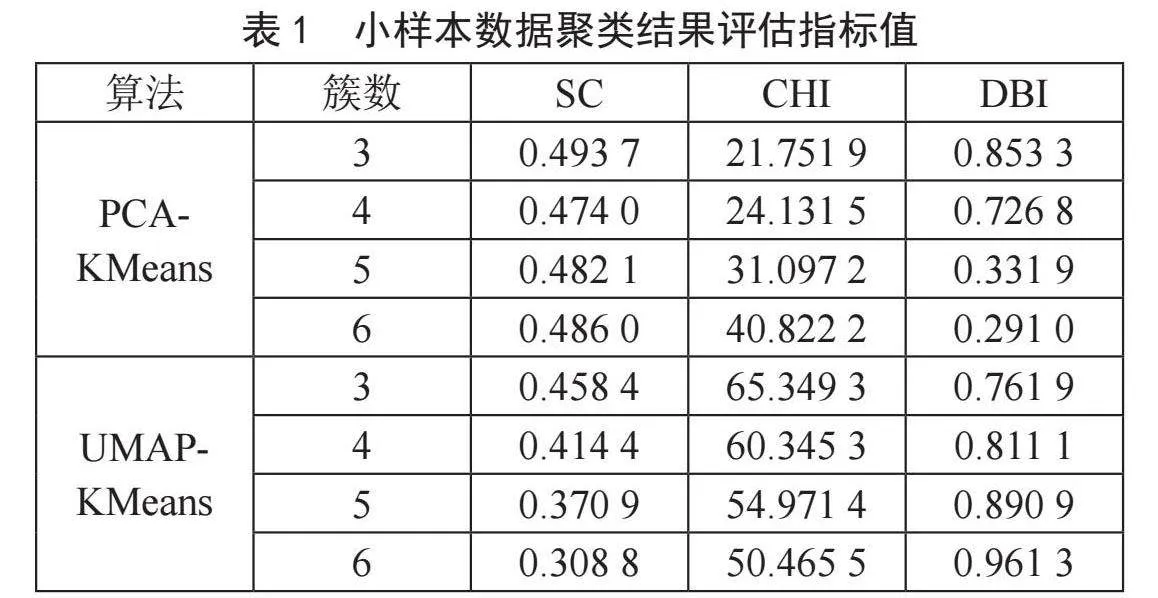
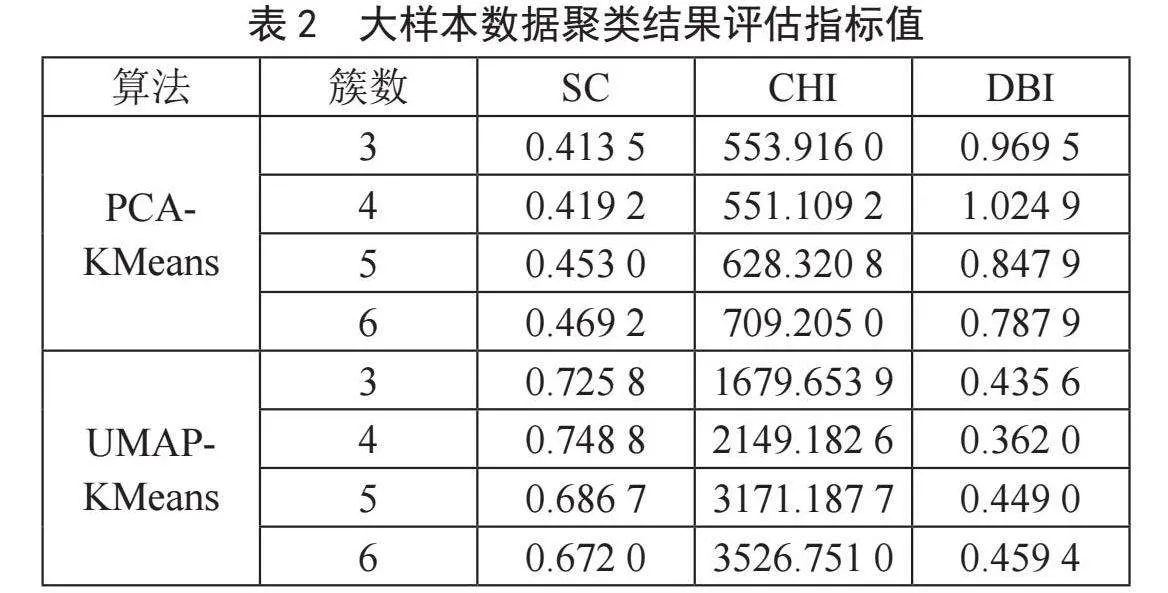
本文采用小样本和大样本数据两类数据进行实验分析,表1、表2显示的是各聚类结果评估指标值。
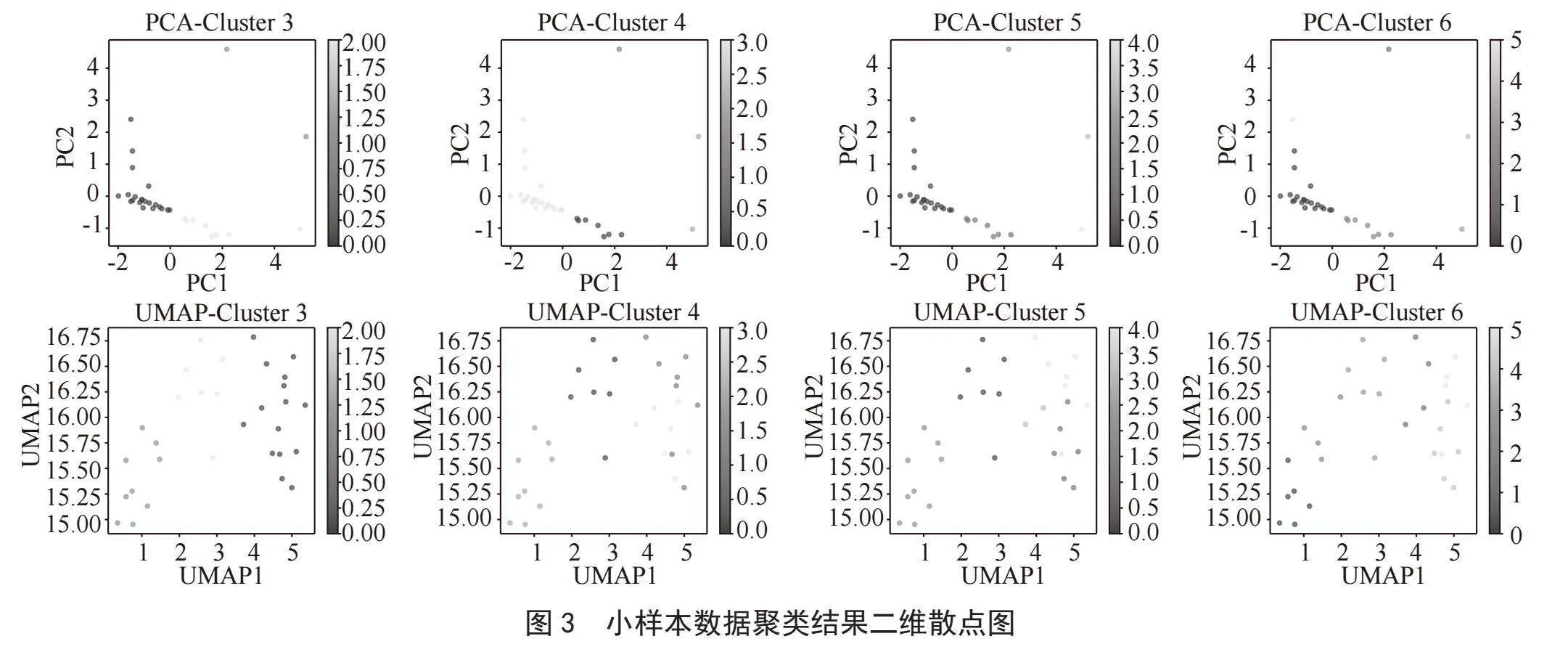
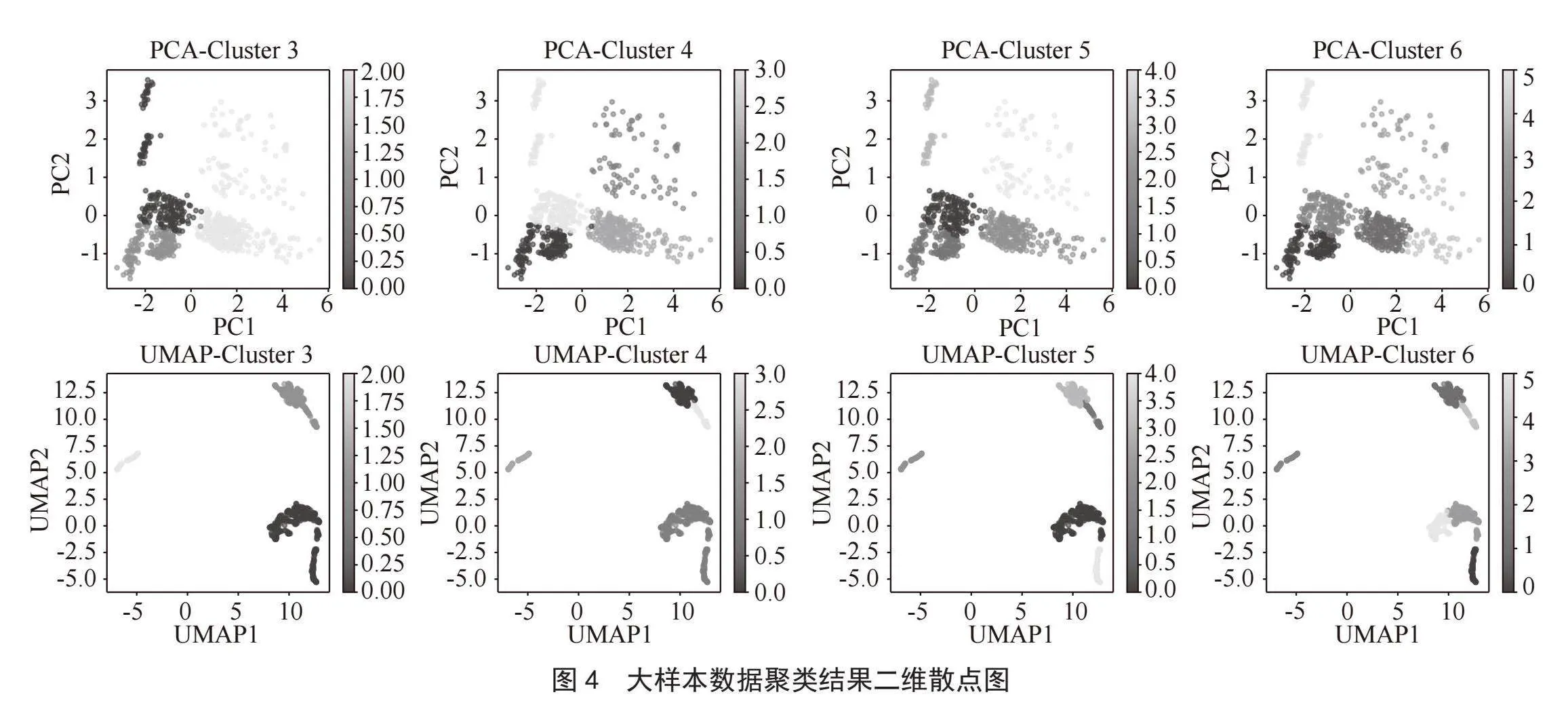
为便于可视化展现不同方法的聚类结果,图3、图4分别展示了小样本和大样本数据在两个降维指标上的聚类结果二维散点图。
4.4.1 模型适应性分析
两个数据样本PCA-Cluster方法下聚类效果比较。SC值较为接近,均分布于[0.4,0.5]区间;大样本数据下的CHI值明显远远大于小样本数据结果;大样本数据下DBI值较小样本数据结果偏大。小样本数据下聚类簇数为5和6时,DBI达到0.331 9和0.291 0,但根据二维散点图可见,聚类簇数为4、5、6时,均存在个别点自成一簇的情况。
两个数据样本UMAP-Cluster方法下聚类效果比较。大样本数据下的SC值普遍高于小样本数据结果,更接近于1;大样本数据下的CHI值明显远远大于小样本数据结果;大样本数据下的DBI值普遍低于小样本数据结果,更接近于0。根据二维散点图,小样本数据下的聚类结果各簇所属点分布错杂,簇内凝聚度及簇间分离度明显较差;而大样本数据下的聚类结果各簇相对集中,各簇边界也较为清晰。
根据比较分析,大样本数据聚类结果较好,说明数据样本量越大,分析效果越好;大样本数据采用UMAP-KMeans分析结果的各评估指标值,达到了较为理想的区间,说明本方法对于地市数据量级的军民通用装备动员企业等级评估问题已具有较好的适用性,而对于更高层级的行政区域,其数据量级更大,故分析效果会更加理想。综上,本方法对于军民通用装备动员企业等级评估问题具有普遍较好的适用性。
4.4.2 企业等级划分
我们根据大样本数据实验结果,对比选出最优聚类方案,并回归原始数据指标进行分析,结合实际需求对企业进行等级划分。
1)优选聚类方案。根据表2,UMAP-Cluster分析结果各评估指标值均明显优于PCA-Cluster分析结果。而在UMAP-Cluster不同簇数的分析结果中,簇数为4时,各评估指标值结果均优于簇数为3时的结果,但对比簇数为5和6的结果,虽SC和DBI值具有优势,但CHI值相对较低。根据二维散点图,簇数为4的聚类结果与簇数为5、6的聚类结果差异主要在于,后两者对一簇已经相对集中的点集进一步做了拆解。
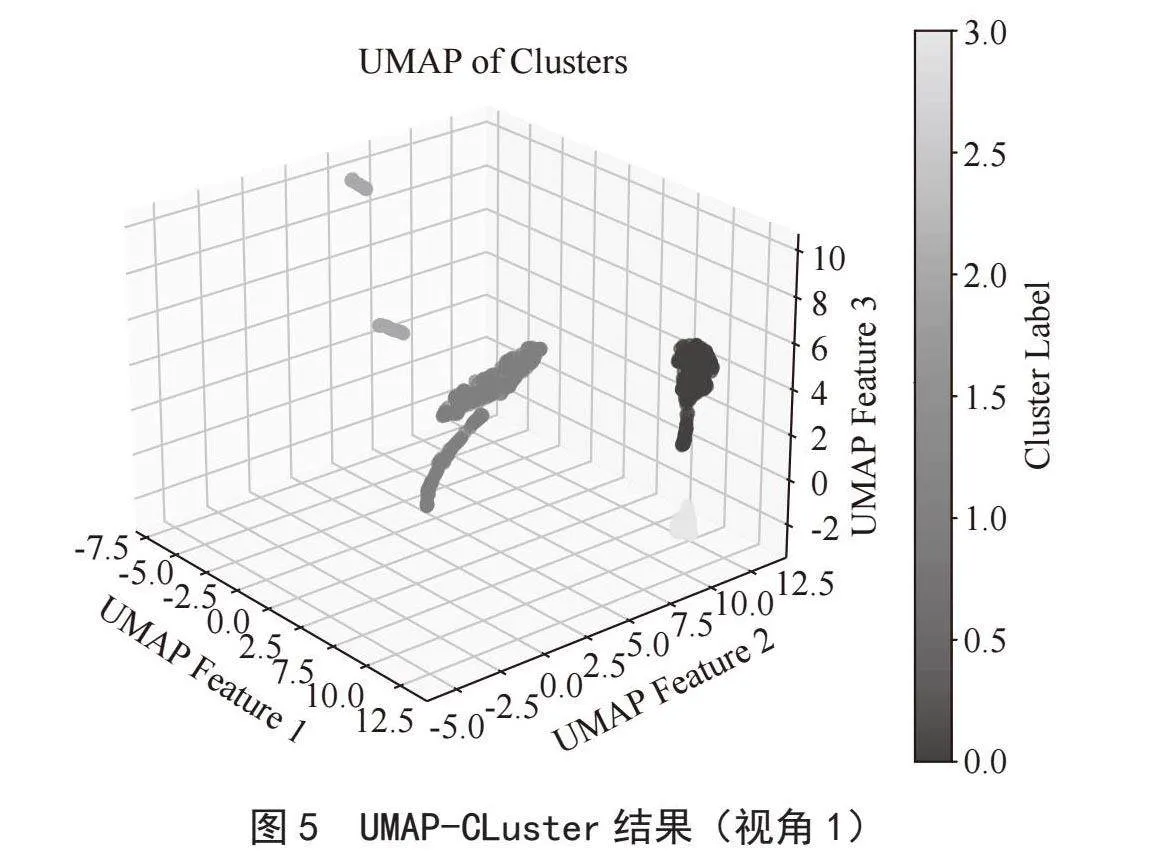
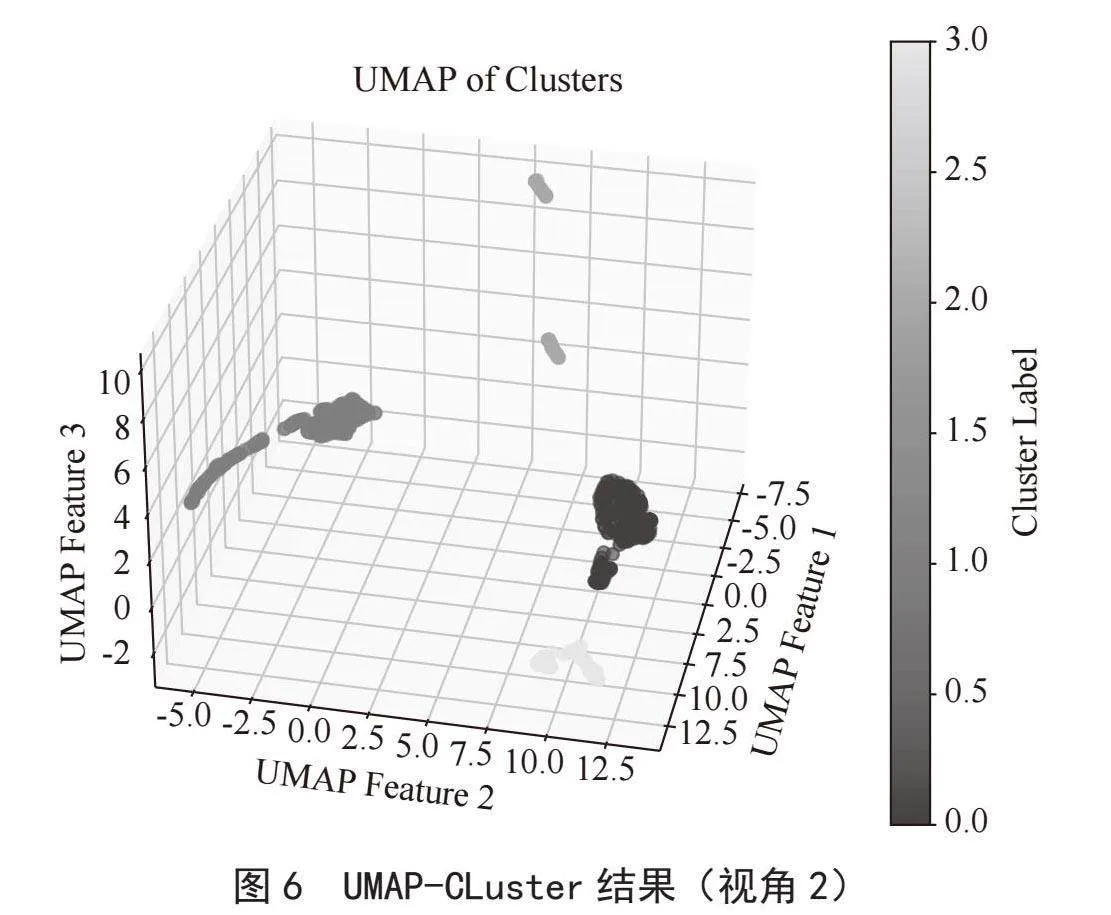
综合评估指标值结果对比及可视化效果观察分析,并出于等级划分不宜过多考虑,簇数为4的聚类方案较为理想,我们据此进行最终企业定级分析。其三维聚类散点图如图5、图6所示。
2)企业定级。我们将该四类企业划分为一级至四级,其中一级为最高级。根据各类别企业指标数值分布区间比较,类别1为国有控股或者国有全资企业,且注册资本、运输能力均较为可观,实际动员过程中,国资企业实力雄厚、可靠度高,应优先作为动员对象,因此,将此类企业划为一级;类别2均为民营企业,但各指标数据均较为可观,此类民营企业综合实力较强,可将其划为二级;类别3为国有控股或者国有全资企业,但综合运输能力较弱,根据潜力调查结果显示,此类别对应企业运营范围较单一,多为特殊材料运输企业,如爆破炸药材料运输企业,此类企业由于特殊营运性质,故保有车辆和驾驶人员较少,鉴于其特殊性及国资性质,将其划为三级;类别0企业各指标数据相较类别1、2企业有一定差距,且均属于民营企业,故将其划定为四级。
5 结 论
本文基于现动员潜力统计指标体系,探索建立了基于不同降维算法(PCA、UMAP)及K-means聚类算法的军民通用装备动员企业等级评估模型,并以公路运输(物流)企业为例,开展了实验分析。实验结果表明,本研究方法对军民通用装备动员供应企业等级评估具有较好的适用性,且数据样本量越大,聚类效果越理想;经过对大样本数据实验结果的进一步分析,对比选用UMAP-Cluster算法下聚类簇数为4的聚类结果作为最优解进行等级划分应用,展示了本方法良好的实用性。
参考文献:
[1] JUVERIA. Data Mining and Clustering: A Technical Overview [J].Global Sci-Tech,2020,12(1):19-23.
[2] 李绍斌,杨西龙,王丰,等.基于主成分聚类分析的战备物资生产能力储备企业选择 [J].军事交通学院学报,2017,19(3):61-65.
[3] 赵阳,周雨晨,王丰.基于国防要求的国家物流枢纽聚类分析 [J].舰船电子工程,2022,42(6):120-127.
[4] 尹泽明,王彩年,王智,等.基于UMAP改进的多域特征提取方法及轴承故障诊断 [J].组合机床与自动化加工技术,2024(1):160-163.
[5] NIE F,LIU H,WANG R,et al. Parameter-Free Multiview K-Means Clustering With Coordinate Descent Method [J/OL].IEEE Transactions on Neural Networks and Learning Systems(Early Access),2024:1-14[2024-01-26].https://ieeexplore.ieee.org/document/10478031.
[6] MUKHOPADHYAY S,KUMAR A,PARASHAR D,et al. Enhanced Music Recommendation Systems: A Comparative Study of Content-Based Filtering and K-Means Clustering Approaches [J].Revue dIntelligence Artificielle,2024,38(1):365-376.
[7] AKSAN F,JASIŃSKI M,SIKORSKI T,et al. Clustering Methods for Power Quality Measurements in Virtual Power Plant [J].Energies,2021,14(18):5902-5902.
[8] RADLIYA R N,FACHRIZAL R M,RABBI R A. Monitoring Application for Clean Water Access and Clustering using K-Means Algorithm [J/OL].IOP Conference Series: Materials Science and Engineering,2019,662(2):022096[2024-01-26].https://iopscience.iop.org/article/10.1088/1757-899X/662/2/022096.
[9] 全国物流标准化技术委员会(SAC/TC 269).物流企业分类与评估指标:GB/T 19680—2013 [S]北京:中国标准出版社,2014.
[10] 李海超,许志超,贾利博.民用物流企业贯彻国防要求保障体系与模式 [J].军事交通学院学报,2019,21(8):58-63.
作者简介:尉迟敬伟(1992—),男,汉族,河北任丘人,硕士研究生在读,研究方向:装备动员;凌海风(1972—),女,汉族,浙江湖州人,教授,博士,研究方向:机器学习、无人机应用;褚德天(1997—),男,汉族,江苏南京人,硕士研究生在读,研究方向:机器学习;康巍(1985—),男,汉族,新疆乌鲁木齐人,硕士研究生在读,研究方向:无人机应用。