
摘 要:对水沙通量变化趋势的预测是沿黄河流域环境治理的基础。鉴于监测技术限制,采集到的含沙量数据相较于水流量数据通常存在大量缺失值,影响对水沙通量变化的精准评估。针对此问题,文章分别采用最邻近、线性、二次样条、三次样条插值方法进行数据补值,并对比插值拟合误差。实验结果表明,采用三次样条插值法进行插值曲线拟合误差最小,经过插值处理后的数据能更好地预测未来水沙通量的变化趋势。
关键词:大数据处理;样条插值;时间序列;趋势预测
中图分类号:TP391 文献标识码:A 文章编号:2096-4706(2024)20-0145-04
Time Series Prediction Algorithm of Water and Sediment Flux Based on Spline Interpolation
ZHANG Ying, YANG Tingyao
(Guangdong Preschool Normal College In Maoming, Maoming 525000, China)
Abstract: The prediction of the variation trend of water and sediment flux is the basis of environmental governance along the Yellow River Basin. In view of the monitoring technology, the collected sediment flux data usually has a large number of missing values compared with the water flux data, which affects the accurate assessment of the variation of water and sediment flux. To solve this problem, the Nearest Neighbor, Linear, Quadratic Spline and Cubic Spline Interpolation methods are used to supplement the data, and the fitting error of the interpolation is compared. The experimental results show that the Cubic Spline Interpolation method is used to minimize the curve error, and the data after interpolation can better predict the future variation trend of water and sediment flux.
Keywords: Big Data processing; Spline Interpolation; time series; trend prediction
0 引 言
水沙通量[1-2]是指单位时间内通过河道某一断面的泥沙量,对其未来变化趋势预测的目的是了解未来河流中泥沙的运移情况,为河流管理提供科学指导。时间序列[3]预测算法是基于对历史时间序列数据规律的挖掘,对未来时间序列规律进行预测。
本文利用黄河某水文站近6年不同时刻水流量与沙流量的实际监测数据,使用4种插值方法对空缺的监测数据进行补值,通过拟合曲线图与误差分析判断最优的插值方法,并将处理后的数据转换成时间序列数据,基于时间序列模型对水沙通量未来趋势进行预测并分析。
1 样条插值方法
已知待插值函数数据处的函数值为f(x0),f(x1),…,f(xn),将相邻两节点进行分段,获得n个插值分段区间,在各分段区间内使用ɑ次多项式Si(x)插值,使其满足插值条件的ɑ-1阶平滑性:
(1)
(2)
三次样条插值[4-5]是根据已知的数据点分割为若干段,利用每段数据拟合一个三次的插值函数,以此计算出空缺的数据点函数值,得到完整的序列数据。该插值方法能实现各分段函数平滑衔接,适用于填充具有周期性和规律性的离散数据。
已知数据集有n+1个数据点,则数据可以分割得到n个区间:
对上方每个区间拟合三次函数,共得到n个三次函数:G(x1),G(x2),…,G(xn-1)。其中,每段的三次函数定义如下:
(3)
其中,xi表示数据集中的第i个数据点,i = 1,2,…,n。每个区间一一对应的三次函数G(x)定义如下:
(4)
其中,方程满足G(x) = yi,i = 0,1,2,…,n。
在满足各分段函数的光滑衔接的条件下,求解方程的系数,通过各段得到的三次插值函数对空缺值进行补值。
2 基于样条插值的数据预处理
2.1 实验数据
本文数据采用位于小浪底水库下游黄河某水文站近6年的水位、水流量与含沙量的实际监测数据。该数据集包括2016—2021年共6年间每天不同时刻的水流量和含沙量数据值,用于对水沙通量趋势进行预测。原始监测数据由年、月、日、时间、水位、水流量、含沙量共7个特征数据列组成。水沙通量为单位时间的含沙量,计算式为:
水沙通量=水流量×含沙量 (5)
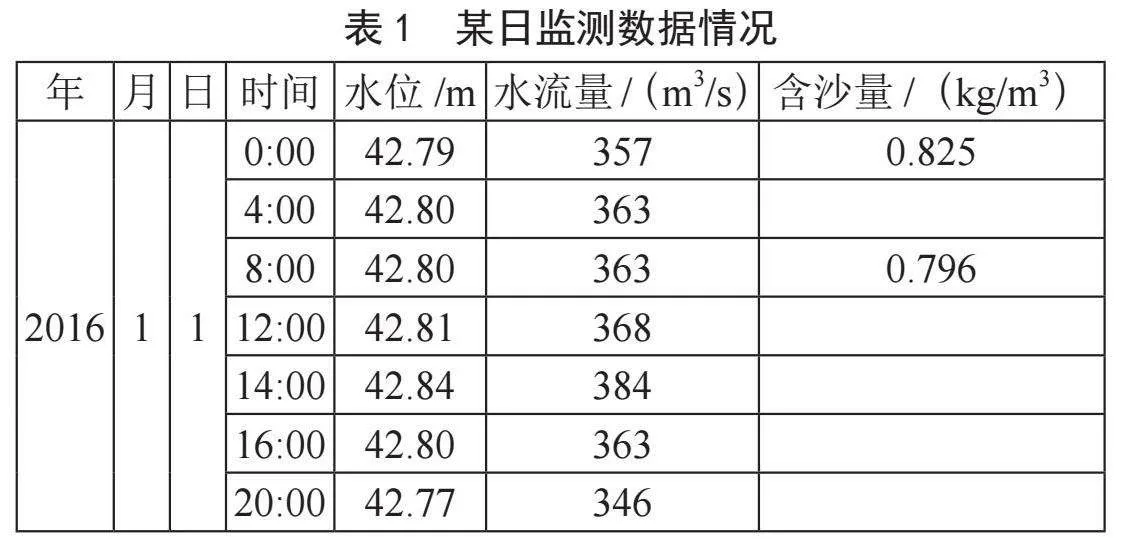
实验数据通过每天监测采集得到,时间间隔为4小时。其中,2016年1月1日监测的数据结构如表1所示,含沙量有5个时刻的数据是空缺的。
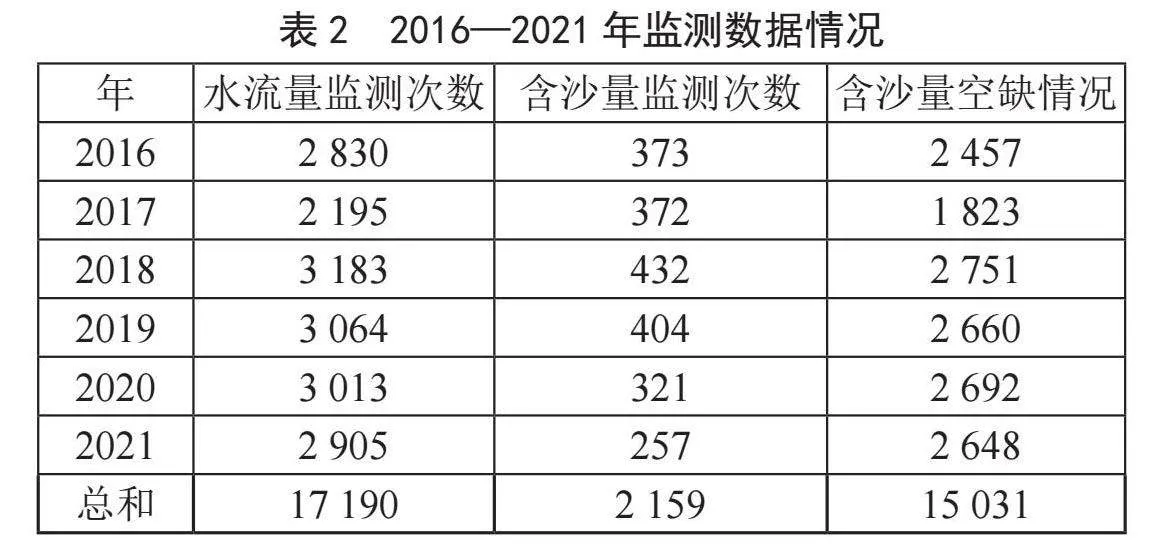
该数据集跨度了6年的时间,每年监测数据情况如表2所示。
由表2可知,每年水流量、含沙量的整体监测次数比较稳定,且相较于水流量数据,监测数据中的含沙量数据存在大量空缺值。若直接对空缺值进行删除处理,会丢失大量采集到的水流量数据,且无法准确地对黄河水沙通量历史数据进行最大程度的信息挖掘。基于数据特性,考虑对含沙量数据进行插值补充,进而获取完整的水沙通量数据,再建立水沙通量的时间序列预测模型。
2.2 数据处理
黄河水域含沙量数据插值处理的步骤如下:
1)将原始数据中的年、月、日、时间这4个特征列信息转换成时序数据,获得“时刻—含沙量”实验数据。
2)分别对含沙量实验数据进行最邻近插值、线性插值、二次样条插值、三次样条插值。
3)利用插值拟合曲线均方根误差和拟合曲线效果,对四种插值方法进行效果评价,选择最优的插值方法对含沙量空缺值进行插值处理。
4)利用水流量数据与插值后的含沙量数据,计算得到水沙通量数据。
5)分析水沙通量时间序列数据的连续性及等间距性,按月份生成水沙通量时间序列数据。
2.3 插值结果对比
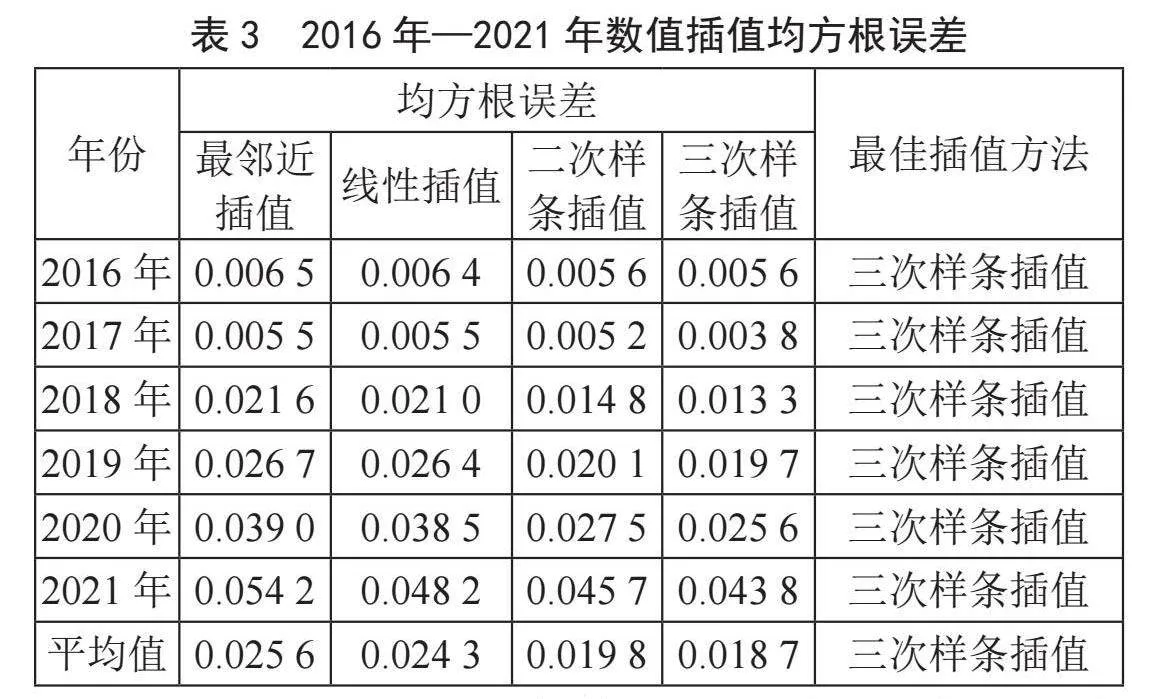
分别利用表3中4种插值方式,对实验数据中空缺是含沙量进行插值。通过计算每种插值方法所得的6年数据插值结果与实际数据的拟合均方根误差,取6年所得的均方根误差的平均值作为插值方法的评价准则,从拟合均方根误差和拟合曲线两个角度分析各个插值方法的效果。
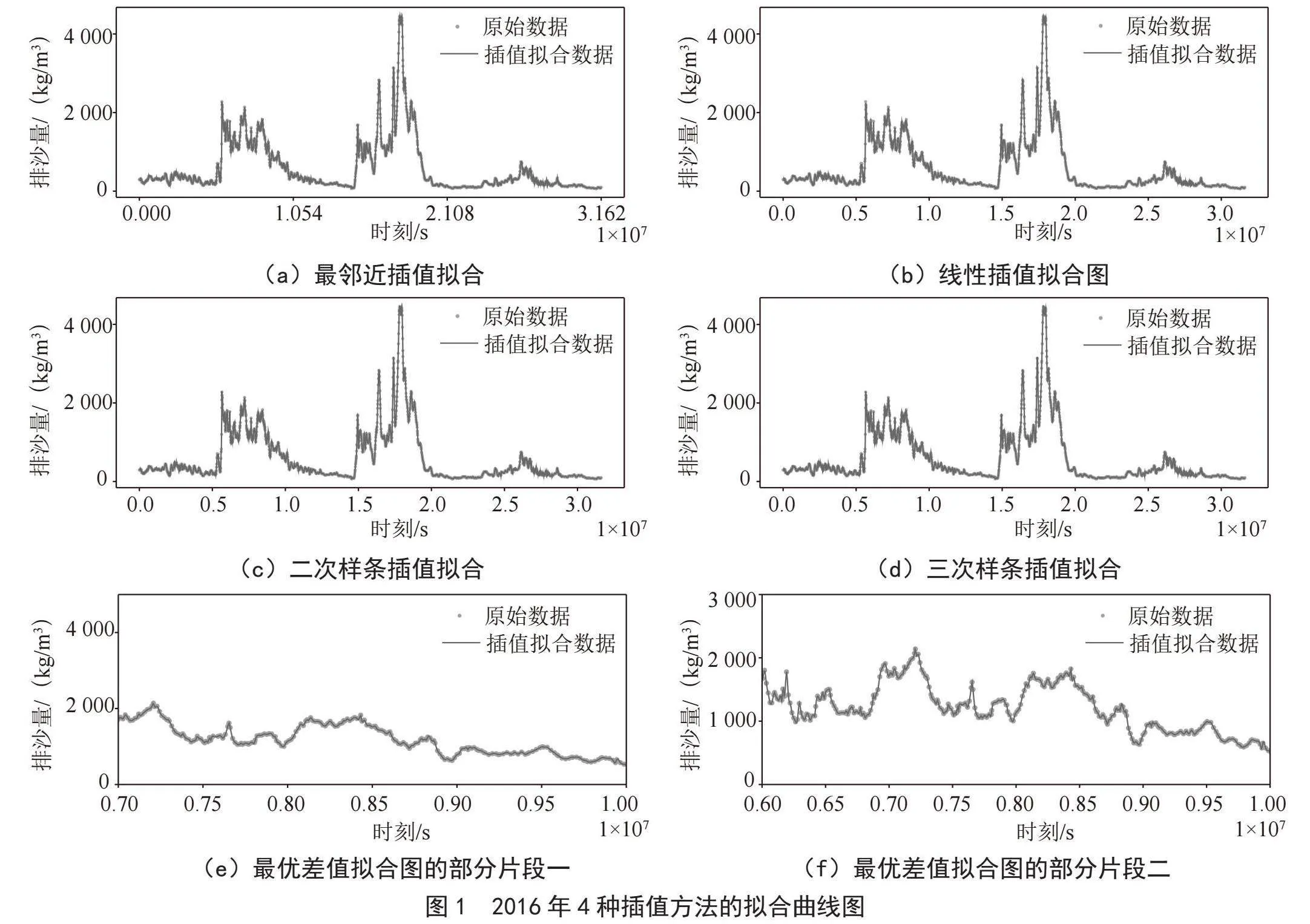
表3中展示了近5年数据分别采用最邻近、线性、二次样条、三次样条进行插值后的拟合误差。可知,拟合数据中三次样条插值方法效果都最优,二次样条插值方法次之,最邻近插值效果最差。图1为2016年数据使用4种插值方法的拟合曲线图及三次样条插值拟合曲线的片段图,由图分析,使用三次样条插值方法进行补植后,可以获取更加连续光滑的时间序列数据。
3 时间序列预测模型
3.1 时间序列分析
基于三次样条插值的黄河水沙通量时间预测模型[6-8],主要从时序数据的平稳性和随机性两个角度进行时间序列分析:
1)时间序列平稳性。基于数据处理得到的月水沙通量时序数据,绘制时间序列的时序图和自相关图可以查看时间序列平稳性。月水沙通量时序数据具有明显的季节性和年周期性,并整体呈下降趋势。由原始数据自相关图体现数据有非平稳性特性,使用季节差分是序列数据平稳化,由差分后的自相关图体现差分后的时间序列自相关图无拖尾现象,接近于平稳,可以用于建立季节性ARIMA模型。
2)单位根和随机性检验。通过单位根检验判断季节差分后时间序列的稳定性,训练模型原始序列的单位根检验的pValue值为0.000 867 1,单位根检验统计量对应的P值显著小于0.05,由此可以判断季节差分后实验数据为平稳序列。
通过Python的statsmodels库内部acorr_ljungbox函数进行检测时间序列是否为随机性序列,检测结果计算得到的P值为0.000 008,远远小于0.05,可知处理后的实验数据是平稳非随机性序列,可用于时间序列模型。
3.2 季节性ARIMA模型
时间序列预测模型的原理是从数据序列数据中挖掘出随机变量随时间变化的趋势,并对未来的数据做出预测[9-10]。通过分析,水沙通量数据属于季节性的时间序列,故采用季节性ARIMA模型,即ARIMA(p,d,q)×(P,D,Q)S。其中,S表示季节周期,p、q表示自回归和移动平均阶数,d表示差分阶数,P、Q表示季节性自回归和移动平均阶数,D表示季节差分阶数。实验研究的月度水沙通量数据属于平稳季节性序列,因此季节周期s = 12,且差分阶数d = 1。
3.3 结果分析与趋势预测
本文使用Python软件,对数据进行插值处理并转换成月度数据,构建基于水沙通量的时间序列预测模型,预测黄河流域水沙通量未来的变化趋势。采用处理后的差分数据训练ARIMA模型,读取AIC值进行模型定阶,确定最优的P值和q值。其中,实验过程中p、q两个参数分别从0、1、2中任意取值,分别计算ARIMA(p,1,q)中所有组合的AIC值,选择AIC值最小的组合作为模型最优参数。
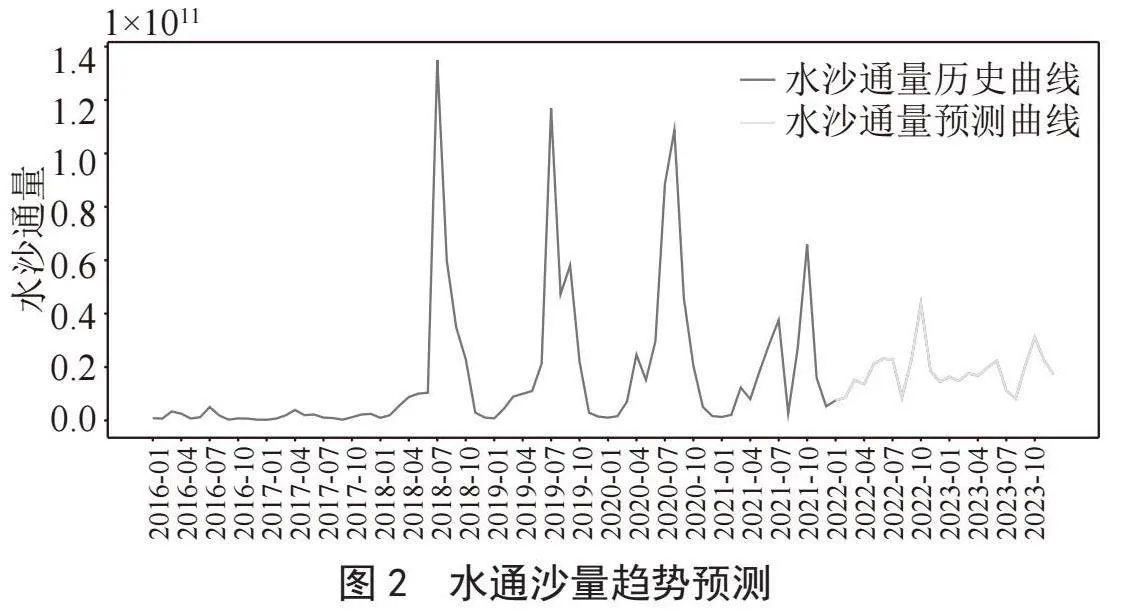
本实验使用网格搜索方法为模型定阶,利用定义的三元参数自动化不同组合对ARIMA模型进行训练和评估。经试验,模型ARIMA(1,1,1)×(1,1,1)12计算得到的AIC值最小,应用ARIMA(1,1,1)模型对未来两年的水沙通量进行预测,预测结果如图2所示。
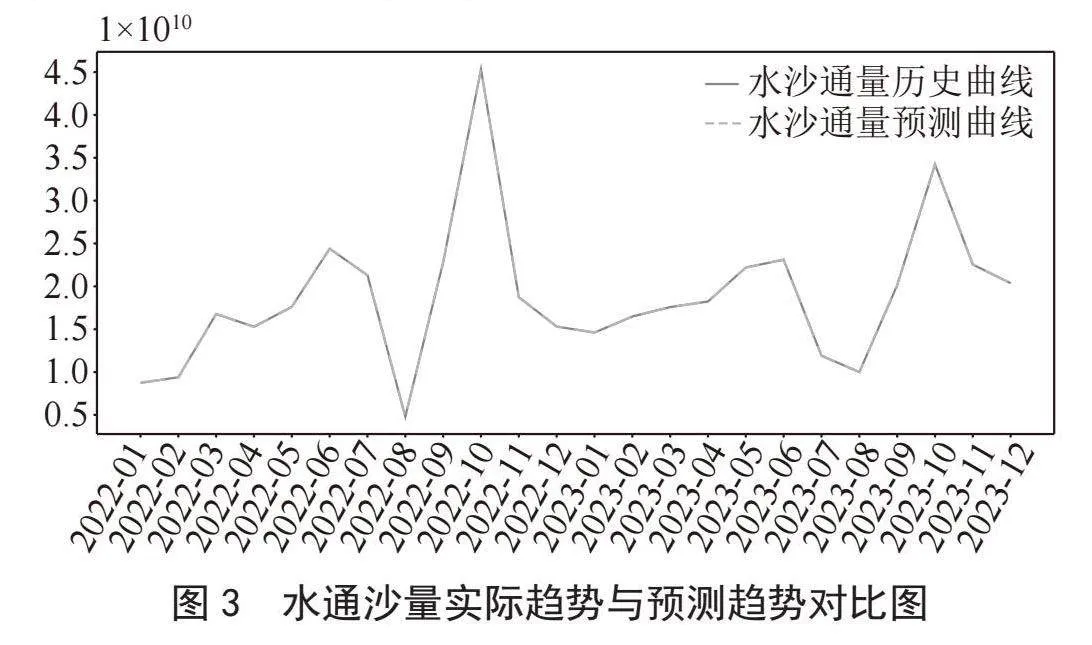
图2绘制的是水通沙量历史趋势与未来预测趋势,蓝色线条是插值补全后2016年至2021年水沙通量的历史趋势,橙色线条是基于历史数据建立时间序列预测模型对2022年至2023年水沙通量未来趋势的预测。对图2进行分析可知,插值处理后的数据能更好体现水沙通量的历史趋势,基于三次样条插值处理后的数据,能用于时间序列预测模型对水沙通量变化规律进行预测,预测结果显示未来两年的水沙通量依然具有季节性变化规律,但整体呈下降趋势,与历史数据呈同一规律变化。图3为水通沙量实际趋势与预测趋势对比图,由历史曲线与预测曲线拟合图可知,基于样条插值的时间序列预测算法对水沙通量趋势预测的结果与实际趋势一致,算法能对未来趋势做出准确的预测,并为评估水沙通量整体变化趋势做出有效决策。
4 结 论
本文对黄河水域监测数据中的空缺值进行了插值与分析,基于不同插值方法的插值结果绘制拟合曲线进行可视化对比分析,并计算各均方根误差进行对比,利用时间序列预测算法进行了检验。结果表明,三次样条插值方法对具有曲线规律的空缺数据集插值效果最优。将样条插值的水沙通量时间序列预测算法应用在其他大数据处理上,既能保证原始数据不受影响的情况下,又能最大程度获取数据信息,使得时间序列预测模型具有更好的算法性能。
参考文献:
[1] 王俊杰,拾兵,巴彦斌.近70年黄河入海水沙通量演变特征 [J].水土保持研究,2020,27(3):57-62+69.
[2] 左书华,杨春松,付桂,等.长江口入海水沙通量变化及其影响分析 [J].海洋地质前沿,2022,38(11):56-64.
[3] 李文,陈佳伟,刘瑞雪,等.张量时间序列预测T-Transformer模型 [J].计算机工程与应用,2023,59(11):57-62.
[4] 唐锦萍.三次样条插值及其在第一类积分方程求解中的应用 [J].大学数学,2022,38(1):5-10.
[5] 吴硕琳,李亚娟,邓重阳.基于PIA的非均匀三次B样条曲线Hermite插值 [J].计算机学报,2023,46(11):2463-2475.
[6] 解建仓,王玥,雷社平,等.基于ARIMA模型的大坝安全监测数据分析与预测 [J].人民黄河,2018,40(10):131-134.
[7] 周坤,许云飞,祁浩伟.基于改进ARIMA的新能源发电短期动态调度模型 [J].电脑与信息技术,2024,32(1):56-61.
[8] 屠立峰,包腾飞,李月娇,等.基于分形插值的ARIMA大坝预警模型 [J].三峡大学学报:自然科学版,2015,37(1):29-32.
[9] 殷文祥.时间序列概率预测分析研究 [D].北京:北京邮电大学,2023.
[10] 郭佳俊.季节性时间序列调整与预测研究 [D].咸阳:西北农林科技大学,2023.
作者简介:张颖(1995—),女,汉族,广东茂名人,助教,硕士,研究方向:数据挖掘、机器学习;杨廷尧(1990—),男,汉族,黑龙江牡丹江人,高级会计师,硕士,研究方向:大数据、会计学。