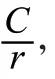





摘" 要:近年来,随着线上教学的不断发展,高校课程呈现多元化趋势,计算机可以起到很好的分析效果。以南京农业大学信息管理学院管理与工程相关专业学生为例,建立能够反映学生的学习成效和教学情况的观测变量,使用结构方程模型(SEM)建立线上学习路径,并通过GA-BP神经网络算法、MATLAB软件对相关数据进行拟合分析,得出线上学习最优路径,提出移动互联网络下大学生最高效学习模式及方案。
关键词:SEM结构方程;GA-BP神经网络算法;线上学习;最优路径
中图分类号:TP39;G434" " 文献标识码:A 文章编号:2096-4706(2024)21-0181-09
Analysis of Learning Effect and Optimal Mode Based on Mobile Internet
—Taking the College of Information Management of Nanjing Agricultural University as an Example
LI Sitong, LIU Yuhan, XU Si, HE Liyang, ZHAO Jikun
(College of Information Management, Nanjing Agricultural University, Nanjing" 210031, China)
Abstract: In recent years, with the continuous development of online teaching, college courses show a diversified trend, and computers can play a very good analysis effect. Taking students majoring in management and engineering in College of Information Management of Nanjing Agricultural University as an example, observational variables that can reflect students learning effectiveness and teaching situation are established, and an online learning path is established using SEM. In addition, through GA-BP neural network algorithm and MATLAB software, this paper fits and analyzes the relevant data to obtain the optimal path of online learning, and proposes the most efficient learning mode and scheme of college students under mobile Internet network.
Keywords: Structural Equation Modeling; GA-BP neural network algorithm; online learning; optimal path
0" 引" 言
近年来,随着线上教学的不断发展,高校课程呈现多元化、复杂化形式。我国大力推行数字化教育,线上教学则属于数字化教育的一种延伸形态。目前我国已存在大学生线上学习行为等相关领域研究,但往往存在调研对象单一、数据集来源可信度不高、优化分析简略等局限性,且该研究暂无加入GA-BP神经网络算法的先例。姜强[1]等研究学者对学习投入利用基于AprioriAll算法和二元Logistic回归分析,研究精准个性化学习路径、提供个性化干预对策;何燕[2]针对E-learning系统中个性化学习路径的优化问题进行了部分仿真模拟实验操作,提出了一种基于Memetic算法的个性化学习路径优化策略,有效提高学习路径的优化效率。
Zhang[3]等研究者提出了一种新的基于最小误差估计的动态学习率,并为调查对象制定出了一种用于单隐层前馈网络在线BP训练的动态学习方案。Muddassar[4]针对目前企业学习评价方法的不足,提出了一种基于BP神经网络的学习能力评价方法,并利用MATLAB神经网络工具箱进行网络学习和样本测试。
本文将使用数据分析软件SPSS、AMOS、Bycharm,结合SEM结构方程模型、GA-BP神经网络算法,以南京农业大学信息管理学院为例,构建理论模型、测量模型,并进行相关数据计算以及趋势预测,同时不断优化调整,对网络空间和映射关系进行保存,最终建立学习路径优化预测模型,分析评估所得学习模型的可靠程度与预测结果,研究得出基于互联网络的最优学习模式。
1" SEM结构方程模型与GA-BP神经网络
1.1" SEM结构方程模型简述
SEM(Structural Equation Modeling),即结构方程模型,作为回归模型的推广,具有传统数据统计分析方法无法比拟的优势:结构方程的潜在变量可以由多个观察指标构成,能够同时对多个变量展开研究;允许自变量有测量误差,参数估计精度更高;具有丰富的拟合评价指标来评价模型[5],在对影响因素、评价指标体系的构建、满意度和竞争力等领域日益复杂化的理论模型的评价分析中,结构方程模型表现出了广阔的应用前景。
1.2" GA-BP神经网络
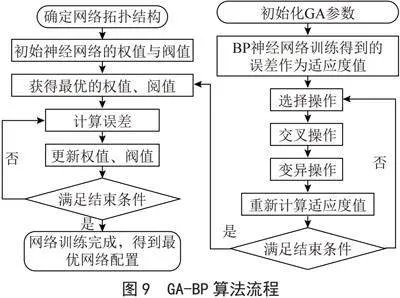
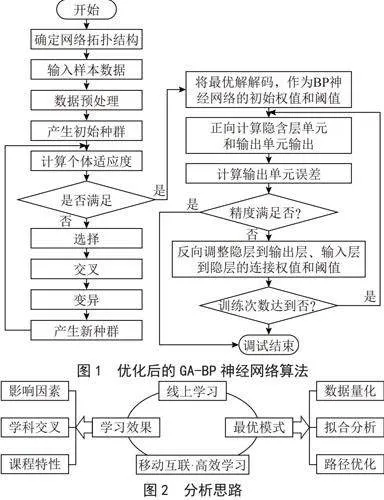
GA-BP(基于GA优化的BP神经网络算法)算法,其包含的两个技术——遗传算法(Genetic Algorithm, GA)和神经网络(Back Propagation, BP)是人工智能技术中的两个分支。遗传算法是一种基于自然选择和基因遗传学原理的群体寻优的搜索算法[6];神经网络是网络模型。BP神经网络具备较好的容错、自适应与泛化特性,如收敛速度慢、算法稳定性较差、样本数量不够全面时训练集容易出现过拟合[7]等。遗传算法在全局搜索方面表现出色,通过遗传算法得到BP神经网络权值和阈值优化求解,就可以得到稳定的网络结构,在图像分割处理、数据计算以及趋势预测方面都有较好的完善和改进,是值得一做的优化方案。为了充分发挥遗传算法和BP神经网络两者的优势,本组通过遗传算法对BP神经网络进行改进优化。优化后的算法如图1所示。研究具体思路分析如图2所示。
2" SEM结构方程模型的研究应用
2.1" 理论基础与分析框架
2.1.1" 理论基础
1)建构主义学习理论。建构主义学习理论强调了学生对知识的主动建构,在线学习这种方式正是满足了建构主义学习理论实践所需的环境条件,并成为学者们通过建构主义模型研究在线学习成效的重要理论依据[8]。学生根据学习需求选择切实有效的网络平台,借由互联网完善自身知识构建,探索个人最优学习路径。
2)人本主义学习理论。马洛斯和罗杰斯[9]是人本主义在教育学领域的代表性学者,他们认为教学活动的重点应该是学生而非教师。正是由于人都有自我实现的需要,才使人的潜能得以激发。
2.1.2" 分析框架
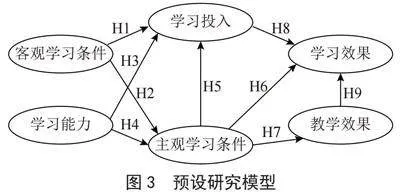
结合互联网络的特征,我们确定了若干潜变量作为预测移动互联网络下学习效果的影响因素,设置了部分中介因素,基于过去学者的研究,提出了本研究的研究模型,模型图如图3所示。
2.1.3" 建立测量模型
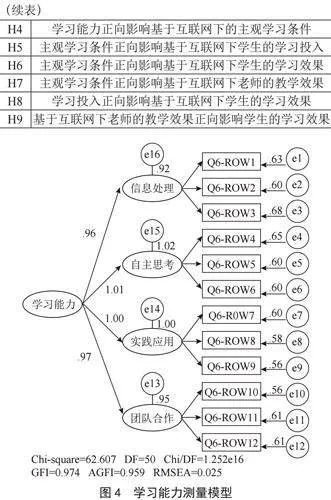
研究小组建立了结构方程模型(SEM)的学习效果、教学效果、学习投入、客观学习条件、主观学习因素和学习能力六个维度的测量模型,表示潜在变量与观测变量之间的关系,整合因素分析与路径分析,其模型的表现形式如式(1)(2)所示。
(1)
(2)
式中Y、X分别为内生观测变量向量和外生观测变量向量,,分别表示Y对η以及X对ξ的回归系数矩阵,即负荷矩阵。
2.1.4" 提出假设
表1为假设项数与假设内容对照表
2.2" 研究设计
2.2.1" 数据来源
由于针对线上学习效果影响因素及其路径优化的研究并没有与之匹配的成熟问卷,因此研究小组结合信管院现实情境以及考虑学习差异性等多方面因素,经过多次讨论后编制了初始问卷,采用了五点量表的形式,问卷的6个潜变量共计73个题项。
研究小组先对问卷进行试测,收集了51份试测数据分析,并根据分析结果删去了信效度不达标和因子负荷量较低的题项3个,并增添学段这个题项,组成了由71个题项组成的正式问卷,最终收集得到400份问卷数据,收集对象为南京农业大学信息管理学院管理科学与工程系相关专业,其中大一、大二、大三、大四占比分别为26%、35%、18%、21%。
2.2.2" 变量及测量问卷设计
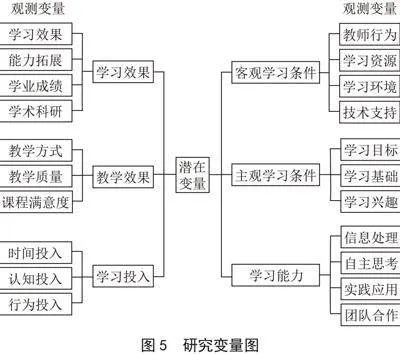
本研究主要测量8个变量。测量的项目均采用五点量表,具体测量项目及其问题如图5所示。
2.2.3" 测量问卷的信度分析
本文建立了包含6个题项总量表,为了保持量表的内部一致性,进行探索性因子分析之前,首先利用样本401份数据,通过计算量表的内部一致性信度系数Cronbachs α(克朗巴哈系数)值进行内部一致性检验,以此检验问卷答案的可靠性。
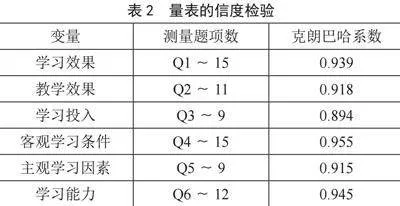
研究小组建立了学习效果、教学效果、学习投入、客观学习条件、主观学习因素和学习能力六个维度的测量模型分别测量它们的克朗巴哈系数,检验六个维度的量表的信度:
从表2中可以看出,学习效果、教学效果、客观学习条件、主观学习因素和学习能力五个潜变量的克朗巴哈系数都大于0.9,说明它们都有很好的测量信度,学习投入的克朗巴哈系数也接近0.9,具有相当的测量信度。这说明本次测量的结果具有较高的一致性、稳定性和可靠性。
2.2.4" 测量问卷的效度分析
由于本量表为本研究小组自行设计的问卷,故先采用了探索性因子分析的效度检验方法。
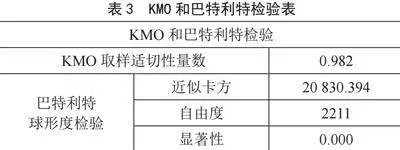
1)KMO和Barlett球形检验验证结果如表3所示,KMO值为0.982,Bartlett球形检验卡方值为20 830.394,显著性水平为0.000<0.001,通过了显著水平为0.1%的显著性检验,即统计检验非常显著。由此可知该量表数据非常适合进行效度和因子分析。
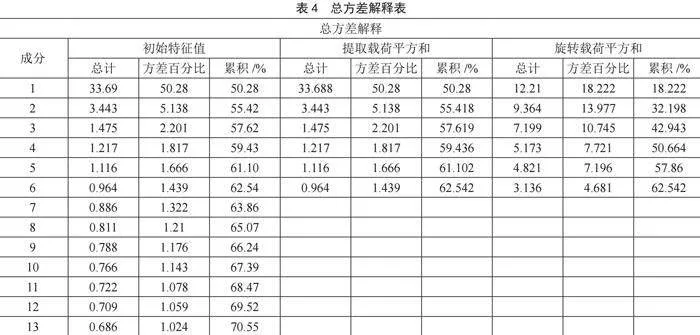
2)因子负荷矩阵与方差贡献率。通过对样本进行探索性因子分析,通过主成分分析的方法提取因子,在大于或接近1的初始特征值因子中,累计方差贡献率达到了62.542%(>60%的标准临界值),说明能够较为充分地反映原始数据;通过正交旋转法提取的共同因子,最终提取其中6个。因子组成与模型中的维度假设并不完全相符,无法确定该量表的结构效度。
2.3" 实证检验-结构方程模型分析结果
2.3.1" 模型的构建和拟合
为探究移动互联网下在线学习影响因素之间的关系和作用路径,本研究运用Amos24.0软件构建结构方程模型,采用最大似然法对初始模型进行估计,初始模型如图3所示,为了进一步检验量表的效度,本研究小组继续对样本数据采用了验证性因子分析的效度检验方法:
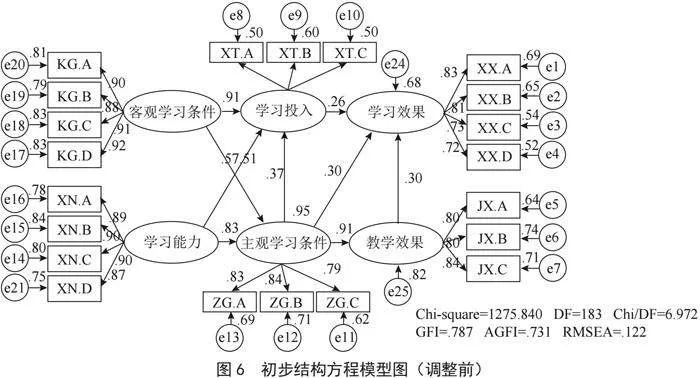
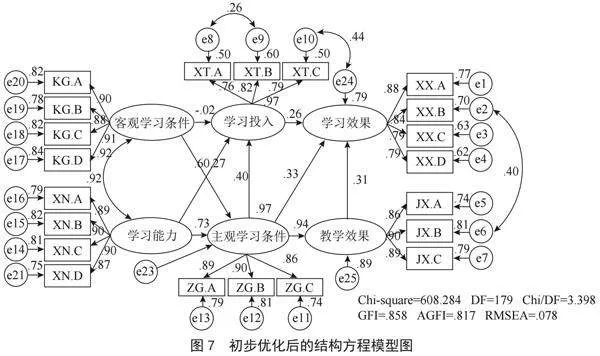
我们将量表数据导入了初步建立的结构方程模型,基于协方差矩阵来分析变量间的关系,假设样本共变异数矩阵 = 模型共变异数矩阵,发现卡方值与自由度之比、近似误差均方根等值并没有表现出很好的拟合效度(如图6、图7所示)。
查询变量间的协方差指标表格发现,外因潜变量直接存在强烈的相关关系,部分残差之间不独立,MI值过大。所以我们将这些相关变量相连,得到了初步优化的结构方程模型。
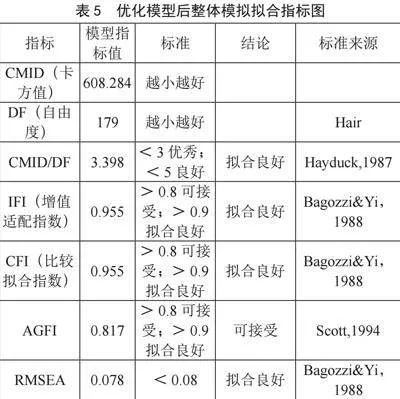
由此结构方程模型,可以得到整体拟合系数表,如表5所示,由下表可知,数据都基本符合标准,六个维度的潜变量的整体结果适配良好,模型的拟合程度在调整后可以接受。
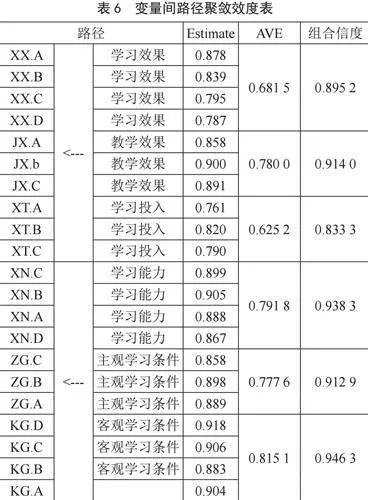
由表6可知,客观学习条件、学习投入、主观学习条件、学习效果、教学效果、学习能力各个潜变量对应各个题目的因子载荷均大于0.7,说明其各个潜变量对应所属题目具有很高的代表性[10]。另外各个潜变量的平均方差变异AVE均大于0.5[11],且组合信度CR均大于0.8,说明聚敛效度理想。
2.3.2" 拟合模型的路径分析结果
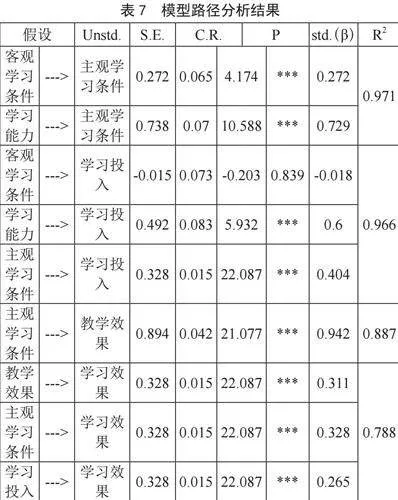
从模型中可以看出,客观学习条件对主观学习条件具有正向影响作用,标化路径系数分别是0.272(p<0.001),学习能力对主观学习条件、学习投入均具有正向影响作用,标化路径系数分别是0.729、0.600(p<0.001)。主观学习条件对学习投入、教学效果、学习效果均具有正向影响作用,标化路径系数分别是0.404、0.942、0.328(p<0.001)。教学效果对学习效果也具有正向作用,标准化系数为0.311,详细如表8所示。
2.3.3" 效应关系和假设验证结果
结构模型验证通过Amos24.0软件计算路径系数及各变量共同解释方差变异(R2),模型验证结果显示,除H1,H2~H9这8个假设均得到了支持(如表7所示)。
分析表8可知,客观学习条件(β = 0.272,p<0.001)、学习能力(β = 0.729,p<0.001)对互联网背景下学习者的主观学习条件均具有显著的正向影响;客观学习条件(β = -0.018,p<0.001)对学习者的学习投入具有不够显著的反向影响,而学习能力(β = 0.6,p<0.001)、主观学习条件(β = 0.272,p<0.001)对学习投入具有显著的正向影响;主观学习条件(β = 0.404,p<0.001)对于教学效果具有显著的正向影响;教学效果(β = 0.311,p<0.001)、主观学习条件(β = 0.328,p<0.001)和学习投入(β = 0.265,p<0.001)均对学习效果具有显著的正向影响。因此接受原假设H2~H9,拒绝原假设H1。
在解释的方差方面,客观学习条件、学习能力两个变量共解释了97.1%的主观学习条件方差变异;客观学习条件、学习能力和主观学习条件三个变量共解释了96.6%的学习投入方差变异;主观学习条件一个变量解释了88.7%的教学效果方差变异;教学效果、主观学习条件和学习投入三个变量共解释了78.8%的学习效果投入方差变异。
2.4" 结果讨论
2.4.1" 对主观学习条件的讨论分析
对路径系数进行分析发现,学习能力对主观学习意愿的影响大于客观学习条,路径系数达0.729,即学习者的学习能力提高一个单位,则他们对互联网背景下的主观学习意愿会提高0.729个单位。互联网络降低了客观条件对主观学习意愿的不利影响;学习能力对主观学习意愿有显著正向作用。
2.4.2" 对学习投入的讨论分析
由AMOS分析得到,客观学习条件对学习者的学习意愿的直接影响相对微弱。学习能力对学习投入的正向影响作用略大于主观学习条件,路径系数达0.492,高于主观学习条件0.328。这说明学习能力更强的学习者往往会产生更多学习投入,强学习者愿意在学习中花费更多时间精力吸收知识以达到较为透彻的学习效果。
2.4.3" 对教学效果的讨论分析
主观学习条件对教学效果的系数为0.942,这说明改善学习者的主观学习条件对于提高课堂教学效果具有显著作用。
2.4.4" 对学习效果的讨论分析
对路径系数分析发现,主观学习条件对学习效果的影响大于学习投入,路径系数0.328,高于学习投入的0.265;学生的主观学习意愿相较于直接的学习投入更能影响最终学习效果。
此外,教学效果对学习效果的影响路径系数达0.311,若教师的教学方式更加契合学生学习模式、教学质量越高、学生对课程的满意度越好,学生在理解知识、掌握技巧、开拓思维等方面的能力将加强,一定程度上提高最终学习效果。
3" 基于GA-BP的学习效果评价模型构建
3.1" 样本集构造
神经网络的样本集包括训练集与测试集,其中训练集用于网络模型的学习与训练,测试集用于检验模型的训练效果并进行优化。样本集的数量对于模型的构建与优化具有显著影响。样本集的构造需要结合问卷的 调查数据集Rn,确定输入变量Xk和输出变量Yk的维数:
(3)
(4)
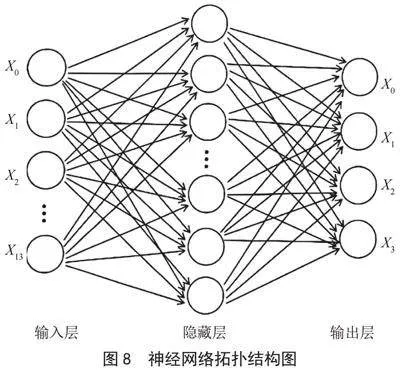
输入向量为影响大学生线上学习效果的14个直接影响因素,分别为时间投入X0、认知投入X1、行为投入X2、教师行为X3、学习资源X4、学习环境X5、技术支持X6、学习目标X7、学习基础X8、学习兴趣X9、信息处理X10、自主思考X11、实践应用X12、团队合作X13;输出向量为体现学习效果的4个维度——学习效率Y0、学业成绩Y1、学术科研Y2、能力拓展Y3。模型使用了70%的样本集(280份)作为训练集,其余121份作为测试集。
3.2" GA优化BP模型
本模型对应的神经网络拓扑结构图如图8所示。
基于GA-BP神经网络参数的优化步骤为:
1)设置BP神经网络络输入层、隐含层和输出层神经元之间的连接权值wij、wjk,隐含层阈值aj、输出层阈值bk、种群规模P、交叉规模N、变异概率Pm、交叉概率Pn的初始值,GA-BP 算法流程图如图9所示。
2)设置遗传算法初始参数值,最大迭代代数、种群数目、交叉概率、变异概率等。
3)采用实数编码制度wij、wjk、aj、bk进行编码,并生成初始种群。
4)计算每一个个体的适应度值:
(5)
式中,yi为网络期望的输出,为实际输出值,SE为误差平方和函数。
5)对种群中的个体进行选择、交叉和变异等操作,产生新一代的种群。
6)判断是否满足寻优结果条件,如果满足,则得到最优个体,并反编码为BP神经网络最优参数,否则转7),继续执行。
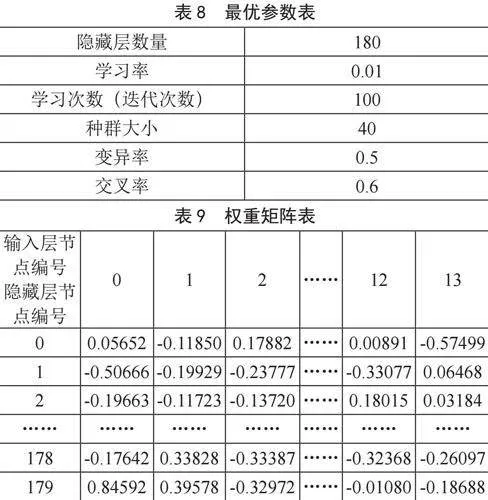
结合问卷实际规模,经过以上步骤的GA寻优完成得到的最佳参数如表8所示,表9为经GA优化的由14个输入节点到180个隐藏层节点的权重(部分表)。
3.3" 评价模型实现度分析—预测评估
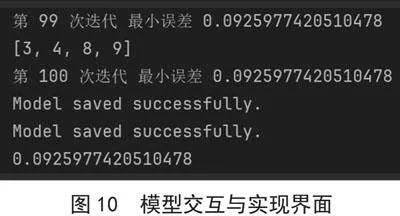
本模型最后通过问答式的输入,将学生的线上实际学习情况之五点量表作为输入端,分别填写X0~X13输入变量的直接相关因子,共计45个题目,本模型交互与实现界面如图10所示。
3.4" 预测变量的误差分析
为了测试模型的精确度,本项目采用MAE(平均绝对误差)与MRE(平均相对误差)两种误差评估方法对该学习效果评价模型的实现度进行误差评估,从而验证其准确性。两种误差的计算公式如式(6)式(7)所示。
(6)
(7)
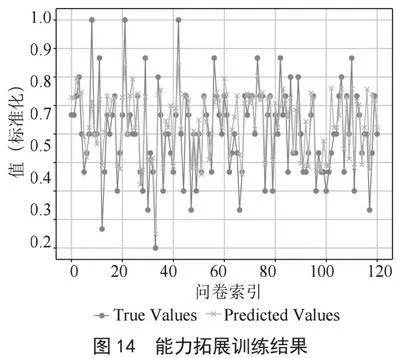
预测模型的误差分析与四个输出变量的训练结果如图11~图14所示。
以上4份输出变量的训练结果图可知,该模型在学习效果的评估上具有良好广泛适应性与数据兼容性,能够体现该生的各个学习能力的平均水平与拓展空间。
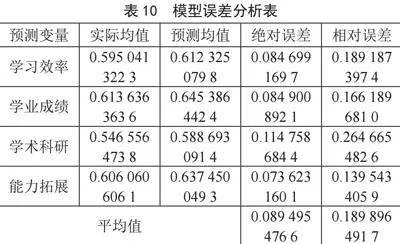
由表10可知,四个输入变量的训练结果的MAE位于10% 以内,整个学习效果评价模型具有良好的可容许误差,因此本模型能够在一定程度上实现对学生线上学习的学习效率与学习能力,也同时反映出了学生在学术科研方面与未来的学习拓展空间的发展潜力,对学生与教师双方都具有良好的能力评估作用。
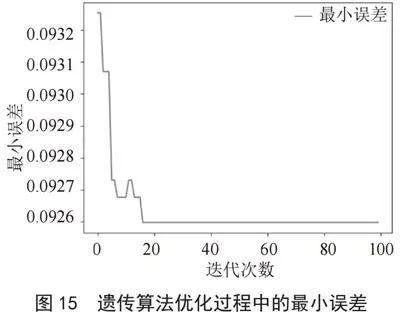
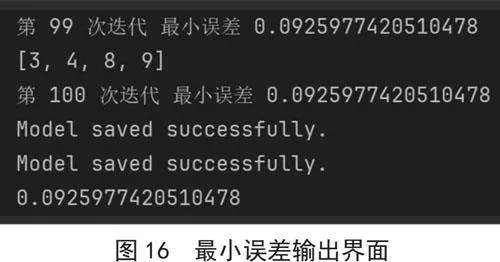
图16为GA优化BP算法过程中的最小误差,此为不断迭代与运行之后的结果,最小误差显示为0.092 597 742 1,始终控制在10%以内,可见此模型具有良好的实现度。
3.5" 研究总结
互联网背景下,学习能力关键性影响学习者的学习策略选择,教育者应借助互联网提升学习者的学习能力。此外,互联网降低了客观条件对学习效果的影响程度,教育资源的分配需要更加注重公平性和个性化。互联网背景下,多因素共同影响学习者的学习效果,学习者与教育者需要共同努力,关注学习者的主观学习条件,引导学习者的自我意识,并结合线上学习的特点以及学习者的实际情况来制定策略,激发其学习的动力和兴趣,提高教学效果同时促进学习者深度学习效果的提升。
在数字化教育普及的时代下,线上教学具有了庞大的可供分析的在线化学习数据,众多数据分析工具被应用于学习分析[12]、个性化学习[13]、教学评价[14]等方面且正在随着社会技术、教育教学的发展而不断迭代与完善,智能控制、自然语言处理、模式识别等人工智能技术是辅助性强,可以很好地帮助人进行深度学习与强化学习,融入教学的资源、环境、评价和管理中。高校应加强人工智能的技术综合作用,迎接人工智能给教育教学带来的新机遇和新挑战,完成人工智能、大数据、学习分析等新技术与教育教学的融合创新[15]。
4" 结" 论
成功建立了一个现实导向、结果可靠的以线上学习效果的细致体现为输入端(14个输入变量,45道测试题),整体学习效率为输出端(综合学习能力的四个体现)的学习效果评价(预测)模型,有助于教师与学生自身完成对学习效果与学习能力的一定程度上的掌握,而误差的存在也给予了学生与教师提升、改进以及挖掘潜力的空间,可是实现双方对于线上教学的效果跟踪与对是否调整上(听)课效果的策略提供可视化数据,具有良好的参考性、实效性与指导性。
本模型适用于与南京农业大学信息管理学院的工程管理、物流管理等学科交叉性较强的综合性专业,模型的数据支持也来源于此。由此可知,模型尚有较大的进步空间,可以依据专业或者学院类型进行灵活性与专业性并存的学习效果评价,具有普遍实用性,且许多延伸性功能也有待开发,例如对于学生自身学习能力的详细剖析与提升学习效果的针对性建议。
参考文献:
[1] 姜强,赵蔚,李松,等.大数据背景下的精准个性化学习路径挖掘研究——基于AprioriAll的群体行为分析 [J].电化教育研究,2018,39(2):45-52.
[2] 何燕.基于Memetic算法的个性学习路径优化研究 [J].电脑与电信,2009(6):47-50.
[3] ZHANG R,XU Z B,HUANG G B,et al. Global Convergence of Online BP Training with Dynamic Learning Rate [J].IEEE Transactions on Neural Networks and Learning Systems,2012,23(2):330-341.
[4] MUDDASSAR S,GHULAM H,MUHAMMAD S, et al. Medical Students Online Learning Perceptions, Online Learning Readiness, and Learning Outcomes During Covid-19: The Moderating Role of Teachers Readiness to Teach Online [J].Int J Environ Res Public Health,2022,19(6):3520-3520.
[5] 王阳,温忠麟,李伟,等.新世纪20年国内结构方程模型方法研究与模型发展 [J].心理科学进展,2022,30(8):1715-1733.
[6] MOMENI E,NAZIR R,ARMAGHANI J D,et al. Prediction of Pile Bearing Capacity Using a Hybrid Genetic Algorithm-based ANN [J].Measurement,2014,57:122-131.
[7] WEI L X,ZHANG Y,JI L L,et al. Pressure Drop Prediction of Crude Oil Pipeline based on PSO-BP Neural Network [J].Energies,2022,15(16):5880-5880.
[8] JONASSEN D,DAVIDSON M,COLLINS M C J,et al. Constructivism and Computer-mediated Communication in Distance Education [J].The American Journal of Distance Education,1995,9(2):7-26.
[9] 冯明珠.人本主义学习理论下的对外汉语中级口语教学 [D].开封:河南大学,2020.
[10] HAIR J F,BLACK W C,BABIN B J,et al. Multivariate Data Analysis 6th Edition [M].New Jersey:Pearson Education,2006.
[11] SWELLER J. Cognitive Load During Problem Solving:Effects on Learning [J].Cogn Sci,1988,12(2):257-285.
[12] 胡琼,姜强,赵蔚.基于数据挖掘的在线学业拖延精准识别及干预实证研究 [J].现代远距离教育,2022(3):46-54.
[13] 韩祎珂,徐彬,张硕.基于认知诊断的个性化习题推荐 [J].计算机应用,2024,44(8):2351-2356.
[14] 韩燕涛.数据驱动下的教师教学绩效改进研究 [D].昆明:云南师范大学,2019.
[15] ZHOU Z H. Open-environment Machine Learning [J].National Science Review,2022,9(8):211-221.
作者简介:李思橦(2002.05—),女,汉族,吉林梨树人,本科在读,研究方向:多元回归分析;通信作者:赵吉坤(1977.08—),男,汉族,山东聊城人,副教授,博士,研究方向:多元回归分析。