




摘" 要:针对遗传算法应用于移动机器人路径规划时存在早熟和收敛慢的问题,提出了一种改进的遗传算法。通过改良初始种群的生成方法,将八叉树与引导函数结合,提高了初始种群的质量;选择操作中采用轮盘赌和精英保留策略相结合的方式,避免了精英个体的丢失而使算法陷入局部最优;在遗传操作中增加修正算子,在不影响进化的同时保证进化后个体的有效性。仿真实验表明,改进遗传算法相比于基本遗传算法,收敛快,寻优效率高,且不易陷入局部最优,整体性能优于基本遗传算法。
关键词:移动机器人;路径规划;遗传算法;改进遗传算法
中图分类号:TP242.6" " " 文献标识码:A 文章编号:2096-4706(2024)23-0180-05
Research on Mobile Robot Path Planning with Improved Genetic Algorithm
LI Zhonglin, JIA Yuting, JIANG Xiaoli
(Software Engineering Institute of Guangzhou, Guangzhou" 510990, China)
Abstract: Aiming at the exsiting problems of precocity and slow convergence when the Genetic Algorithm is applied to mobile robot path planning, an improved Genetic Algorithm is proposed. By improving the generation method of the initial population, the octree is combined with the bootstrap function to improve the quality of the initial population. The combination method of roulette and elite retention strategy is used in the selection operation to avoid the algorithm falling into the local optimum due to the loss of the excellent individuals, and the correction operator is added in the genetic operation to ensure the the individual validity after evolution" while not affecting the evolution. Simulation experiments show that the improved Genetic Algorithm, compared with the basic Genetic Algorithm, converges quickly, has high efficiency in finding the optimum, and is not easy to fall into the local optimum. It is better than the basic Genetic Algorithm in the overall performance.
Keywords: mobile robot; path planning; Genetic Algorithm; improved Genetic Algorithm
0" 引" 言
随着移动机器人技术的快速发展,其在各个领域的应用日益广泛,如物流、医疗、服务等领域。在这些应用场景中,路径规划是移动机器人的一个核心问题,直接关系到机器人的工作效率和安全性。传统的路径规划方法,如人工势场法[1]、D*算法[2]、A*算法[3]等,虽然取得了一定的效果,但在处理复杂环境和实时规划方面仍存在一定的局限性。因此,研究一种高效、稳定的路径规划方法具有重要的实际意义。遗传算法具有适应性高和鲁棒性强的特点,是一种优良的全局优化搜索算法,被广泛应用于复杂的优化问题[4-5]。然而,基本遗传算法在搜索过程中易陷入局部最优解和收敛慢[6]。为此,对遗传算法进行改进,以提高其搜索效率和优化能力以及适应移动机器人路径规划问题。
1" 环境建模
环境建模是实现路径规划的前提,首先要对移动机器人的工作环境建模,常用的建模方法有栅格法、路标法以及可视图法[7]。其中,栅格法具有简单灵活易于处理的优点[8],选用栅格法建模。
1.1" 栅格法环境建模
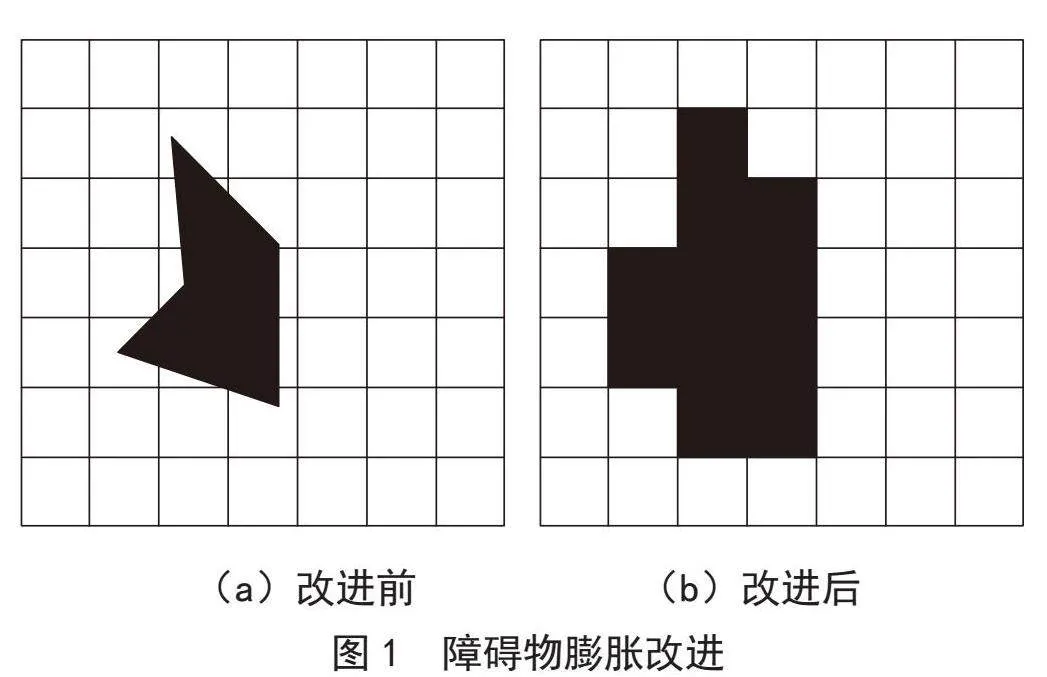
栅格法是用等大的正方形栅格对移动机器人的工作环境进行分割。如图1(a)所示,用等大的栅格以俯视的角度将工作环境栅格化,其中,黑色部分为障碍物,白色部分为可行路径。其中,栅格的大小表征环境模型的精细程度,栅格越小,环境模型越精细,越接近真实环境,但栅格划分过于精细,则对计算机算力要求高,影响路径规划速度[9]。一般地,以移动机器人边沿任意两点连线的最大距离作为栅格的边长。
用栅格分割移动机器人的工作环境后,如图1(a)所示,会出现三种类型的栅格:栅格被障碍物完全覆盖、栅格被障碍物部分覆盖和栅格未被障碍物覆盖。为避免移动机器人与障碍物碰撞,将障碍物膨胀改进,如图1(b)所示,规定:被障碍物完全覆盖的栅格记为障碍栅格,未被障碍覆盖的栅格记为自由栅格,被障碍物不完全覆盖的栅格,仍记为障碍栅格。障碍栅格移动机器人不可行走,用黑色栅格表示,自由栅格移动机器人可行走,用白色栅格表示。设工作环境分割得到M行N列栅格,(x0 y0)表示栅格的初始位置S,(xM yN)表示栅格的目标位置G,全部栅格构成的集合用A表示,如式(1)所示:
(1)
栅格(xy)所含的信息是障碍物还是可行栅格,用f(xy)表示,如式(2)所示,如该栅格为障碍栅格,则函数值为1,如该栅格为自由栅格,则函数值为0。
(2)
1.2" 栅格标识
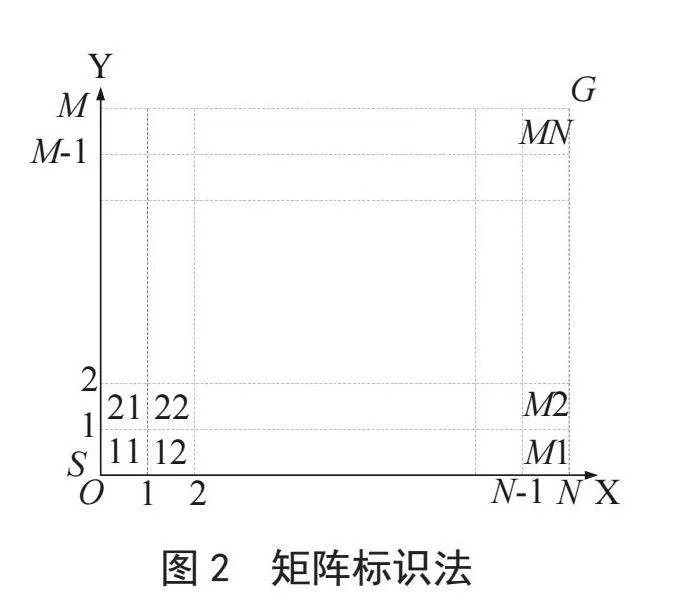
直角坐标法[10]是常用的栅格标识方法,其特点是直观明了,但不利于染色体的形成及遗传操作,故在此基础上改进为矩阵标识法,如图2所示。矩阵标识法以栅格作为基本单位,将移动机器人的工作环境横向划分为M个栅格,纵向划分为N个栅格,横向从左向右用阿拉伯数字标注序号,纵向从下向上用阿拉伯数字标注序号。根据栅格所处的横纵栅格序号确定其矩阵坐标,如栅格A所处位置是横向第a个栅格和纵向第b个栅格,记作ab。为便于观测与计算,给出矩阵坐标与直角坐标转换公式,以栅格A为例,如式(3)所示:
(3)
其中,a、b分别表示栅格A横轴和纵轴的栅格序号;xA、yA分别表示栅格A的直角坐标。
1.3" 行走方式
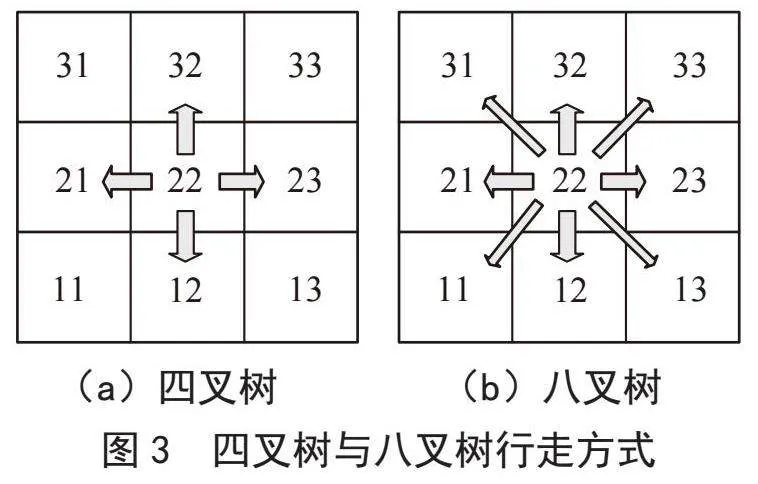
行走方式是指移动机器人在栅格环境中移动的规则,四叉树和八叉树是移动机器人两种基本的行走方式[11]。四叉树行走方式如图3(a)所示,移动机器人从当前栅格向下一个栅格移动时,可选择向左、向右、向上、向下四个方向。八叉树行走方式如图3(b)所示,移动机器人除了选择四叉树中的四个方向外,还可以选择四个斜行方向,左上、右上、左下、右下。因为八叉树行走方向更多,又因其存在斜行方式,所形成的路径更短,所以选用八叉树的行走方式。
1.4" 行走规则
移动机器人按照八叉树的方式行走,在t时刻,移动机器人的位置为(XtYt),在t-1时刻,移动机器人的位置为(Xt-1Yt-1),两位置坐标应符合以下规则:
(4)
(5)
(6)
移动机器人行走的前后两个时刻的位置坐标必须满足式(4)和式(6)或式(5)和式(6),即移动机器人沿横向坐标移动一个栅格或沿纵向坐标移动一个栅格或斜向行走一个斜向栅格。
移动机器人的路径规划是为了获取一条最短的安全路径,路径长度用函数obj表示,即将每两个时刻之间路径长度累积,计算方法如式(7)所示:
(7)
其中,St表示连续两步之间的距离。一个栅格的长度记为单位1,移动机器人沿坐标轴移动时,每移动一次的路径长度为1,当移动机器人斜向移动时,每移动一次的路径长度为。
2" 改进遗传算法
基本遗传算法是一种优异的智能寻优算法,但在使用基本遗传算法规划路径时易出现收敛慢和早熟的现象,为此,需设计一种改进遗传算法,为移动机器人路径规划提供一种新的思路和解决办法。
2.1" 染色体编码
染色体编码采用二进制编码方式。在使用二进制编码时,首先将栅格坐标依次序连接起来形成路径,如ab,cd…mn。然后,将路径中的每个栅格坐标值用二进制数表示,即为染色体,从而完成染色体编码。其中,用二进制数表示位置坐标时所采用的二进制位数以当前环境模型中的终点坐标所需用的最大二进制位数为基准,其他坐标均按照该二进制位数表示。
2.2" 初始化种群
初始化种群采用八叉树与引导函数的相结合的方式。从起始栅格出发,按八叉树原则选取与起始栅格相邻的自由栅格作为下一个路径栅格,当可供选择的自由栅格为多个时,需计算引导函数的值,引导函数如式(8)。将所有自由栅格的引导因子计算后,采用赌盘策略来选定栅格。规定在一条路径中,当栅格被选定后,标记该栅格,在后续路径规划中不会被再次选择,以避免产生循环路径。
(8)
H(xa yb)的值表示自由栅格的(xa yb)的引导因子,其值的大小反映了该自由栅格被选中的概率;(xM yN)为目标栅格的坐标。
2.3" 适应度函数
适应度函数以路径总长的倒数作为适应度函数,记作F,如式(9)。对于路径规划,路径总长度越短越好,即F越大越好。
(9)
式中i为示路径的序号,St为t时刻和t-1时刻之间的欧式距离。
2.4" 遗传操作
遗传操作包括选择、交叉、变异和修正操作,其中选择操作使用轮盘赌和精英保留策略相结合的方式,交叉操作使用单点交叉算子,变异操作使用基本位变异算子,修正操作用于判断和修复个体。
2.4.1" 选择算子
选择算子采用轮盘赌和精英保留策略相结合的方式[12]。在轮盘赌选择中,个体被选择的概率与其适应度成正比,种群中适应度高的个体易被保留,适应度低的个体易被淘汰。当种群中产生最优个体时,如仅使用轮盘赌选择,存在最优个体参与下一轮进化时而被破坏的现象,可能使算法收敛于局部最优解,因此轮盘赌选择需结合精英保留策略使用。种群的每次进化时均使用精英保留策略将最优个体保存,同时保证该个体继续参与进化,当有适应度更高的染色体出现时,将原保留的个体用该个体替换,以保证最优个体不丢失且始终保持最优,弥补轮盘赌选择的不足。
2.4.2" 交叉算子
交叉操作选用单点交叉[13]的方式。按照设定的交叉概率,首先选择两个父代个体,在它们之间对应位置随机选择一个点,利用该点将两父代个体的基因序列一分为二;然后将这两个父代个体的后半部分基因交换,从而形成两个新的个体,完成交叉操作。通过交叉算子能够生成新个体,新个体来自上一代种群,而不同于上一代种群中的个体,从而实现算法的全局搜索。
2.4.3" 变异算子
交叉操作采用基本位变异[14]的方法。交叉操作按照较小的概率进行,按照设定的变异概率,将选中个体的某位基因由零变一或由一变零,以改变该位的基因值,从而产生新的个体。通过变异操作也可以产生新的个体,但因变异操作的概率较小且染色体变动不大,完成了在遗传进化过程中进行局部搜索的作用。
2.4.4" 修正算子
修正算子用于判断个体是否为有效路径及修复个体。当种群完成交叉和变异操作后,所生成的新种群中部分个体可能会存在障碍栅格,即为无效路径。无效路径如被随意删除将影响种群的多样性,不利于算法的收敛,此时需使用修正算子对个体进行修复。当个体中存在一个障碍栅格时,对障碍栅格相邻的两个自由栅格分别使用八叉树行走方式确定交叉栅格,如交叉栅格只有一个,则用其替代障碍栅格,如交叉栅格有多个,每个交叉栅格对应一个有效路径,此时需计算每个有效路径的适应度值,选择适应度值最高的个体代替原个体,如适应度相同,则随机选择一个个体。当个体中存在多个障碍栅格时,则自左向右依次按照一个障碍栅格的方法来处理。
3" 实验与分析
改进算法的可行性和有效性需通过实验验证。使用MATLAB 2015b在配置为2.4 GHz、酷睿i5处理器、Windows 11家庭中文版的戴尔Inspiron 15 3511计算机平台上,对其进行计算机仿真实验,并与基本遗传算法进行比较。工作环境为20×20的栅格环境,改进算法与原算法主要参数设置如下:种群规模M = 200,交叉操作的概率Pc = 0.6,变异操作的概率Pm = 0.05,最大进化代数T = 100。
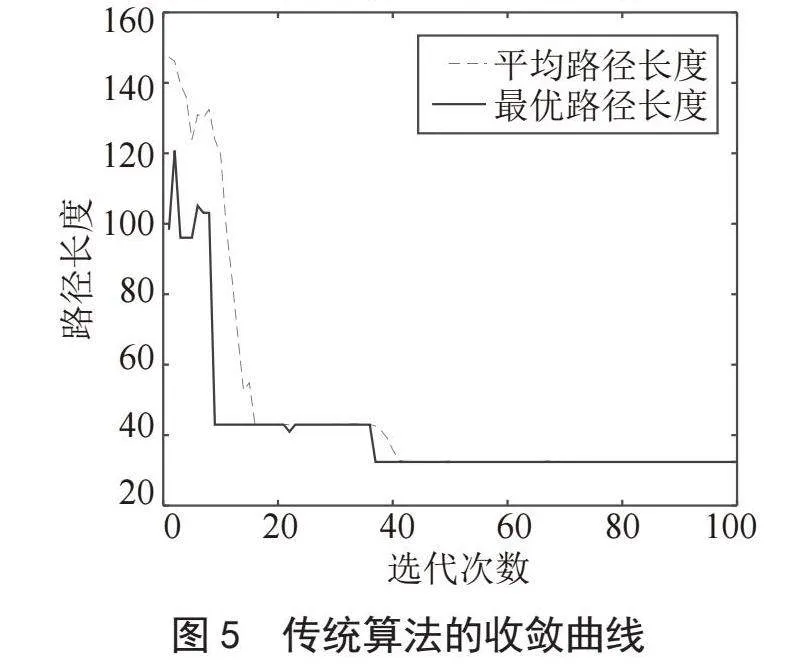
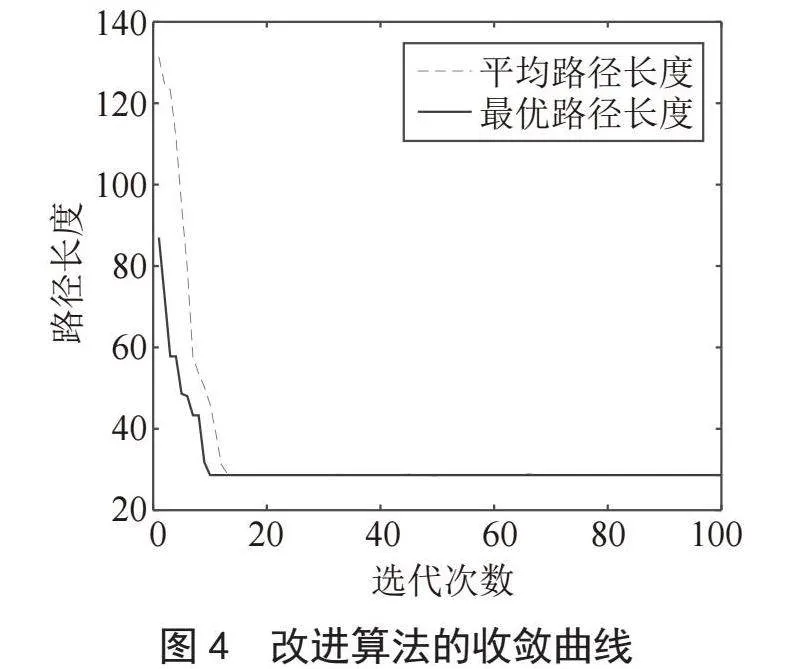
图4、图5分别为两种算法的收敛曲线,图6、图7分别为两种算法的路径规划图,对比可得:基本遗传算法在第37代收敛,规划路径长度为32.8,陷入局部最优解,改进遗传算法在第10代收敛,规划路径长度为28.63,搜索到全局最优解。在相同的工作环境和参数设定情况下,改进遗传算法的收敛的更早,并且没有陷入局部最优解。
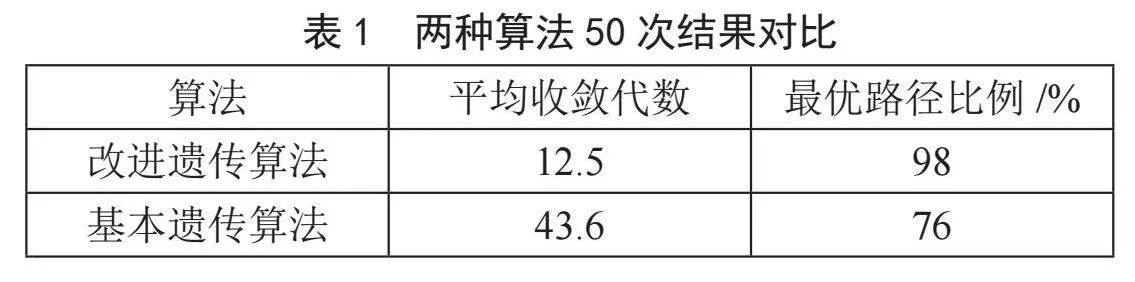
单次实验具有随机性和不确定性,为确保改进算法的有效性,按照原参数对两种算法分别进行50次实验,计算其平均收敛代数和最优路径比例,实验结果如表1所示。从表中可以看到,50次实验中,改进遗传算法平均收敛代数为12.5,小于基本遗传算法的43.6,寻到最优路径的比例为98%,高于基本遗传算法的76%。因此,改进遗传算法相比于基本遗传算法在规划路径时收敛更快,寻优效率更高,且不易陷入局部最优,能有效地解决了基本遗传算法早熟和收敛慢的问题。
4" 结" 论
为解决基本遗传算法的早熟和收敛慢及对移动机器人路径规划的适应性,对基本遗传算法进行了改进。在种群初始化时将八叉树与引导函数结合,提高了初始化种群质量;选择操作中采用轮盘赌和精英保留策略相结合的方式,能避免精英个体的丢失而使算法陷入局部最优;在遗传操作中增加修正算子,能在不影响进化的同时保证进化后个体的有效性。改进遗传算法在规划路径时收敛更快,寻优效率更高,且不易陷入局部最优,能有效地解决基本遗传算法存在的问题。
参考文献:
[1] 梅艺林,崔立堃,胡雪岩,等.基于人工势场法的复杂环境下多无人车避障与编队控制 [J/OL].工程科学学报,2024:1-14[2024-12-03].http://kns.cnki.net/kcms/detail/10.1297.TF.20240830.1126.002.html.
[2] 秦旭,黄晓华,马东明,等.基于改进D*算法的巡检机器人路径规划 [J].组合机床与自动化加工技术,2022(6):10-13.
[3] 王慧婷,余萌,李昱叶,等.月面南极巡视器自主导航路径规划算法 [J].深空探测学报:中英文,2023,10(6):598-607.
[4] HART P E,NLSSON N J,RAPHEL B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths [J].IEEE Transactions on Systems Science and Cybernetics,1968,4(2)):100-107.
[5] 闫永权.基于注意力机制的云数据中心资源消耗预测 [J/OL].武汉大学学报:理学版,2024:1-10[2024-11-28].https://doi.org/10.14188/j.1671-8836.2024.0031.
[6] ZHUANG X Q,ZHUANG S Q,SU D M,DU S,et al. TPS-Genetic Algorithm for Real-Time Sailing Route Planning based on Potential Field Theory [J].European Journal of Engineering and Technology Research,2023,8(3):86-99.
[7] 许赫威,戴晓强,王莹,等.改进分布估计算法的AUV全局路径规划 [J].传感器与微系统,2024,43(7):47-50.
[8] 韩书豪.基于实时分布式模式的多机器人协同运动控制 [D].西安:西安电子科技大学,2021.
[9] 周雷.基于改进鲸鱼优化算法的无人机航迹规划技术研究 [D].南昌:华东交通大学,2023.
[10] 龚铭凡,徐海祥,冯辉,等.基于改进蚁群算法的智能船舶路径规划 [J].武汉理工大学学报:交通科学与工程版,2020,44(6):1072-1076.
[11] 杨朝棚.海流环境下的无人艇路径规划研究 [D].厦门:集美大学,2024.
[12] 黄荣杰,王亚刚.基于可视图与改进遗传算法的机器人平滑路径规划 [J].控制工程,2024,31(4):678-686.
[13] 杨寅泽,柯俊.基于GA优化神经网络的变刚度复合材料板簧刚强度预测研究 [J].软件工程,2024,27(7):17-21.
[14] 张滕飞,金晓辉,朱汗青.基于改进朴素贝叶斯的武器装备性能预测 [J].军事交通学院学报,2021,23(5):23-27.
作者简介:李忠林(1990—),男,汉族,江苏连云港人,助教,硕士,研究方向:智能控制与算法。

