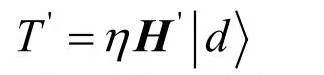





摘" 要:在光学信息安全领域,计算鬼成像(CGI)技术作为一种新兴的单像素成像(SPI)技术,因其数据压缩和实值密文的加密性能而显示出巨大潜力。然而,现有的基于计算鬼成像的加密技术存在解密结果噪声严重、密钥数量庞大以及复振幅图像成像效果不理想等问题。为解决这些问题,文章提出了一种基于随机正交调制的单像素复振幅成像加密方案。该方案利用正交复数矩阵逆变换的方法实现了复杂复振幅物体的成像,同时使用两个随机整数序列作为密钥扰乱正交复数矩阵,从而实现对原始图像的加密。这不仅增强了系统的安全性,还大幅减少了传输密钥的数量。后续的仿真实验验证了该方案的可行性和安全性,该方案能够抵御一些常见的噪声干扰,展现出良好的鲁棒性。
关键词:图像加密;复振幅成像;正交矩阵;随机调制
中图分类号:TP309.7" 文献标识码:A" 文章编号:2096-4706(2025)03-0177-06
Research on Single-pixel Complex Amplitude Imaging Encryption Scheme
ZHANG Heng
(School of Information Engineering, North China University of Water Resources and Electric Power, Zhengzhou" 450046, China)
Abstract: In the field of optical information security, Computational Ghost Imaging (CGI), as an emerging Single-Pixel Imaging (SPI) technique, shows great potential due to its data compression and encryption performance of real-valued ciphertext. However, the existing encryption techniques based on computational ghost imaging have serious noise in the decryption results, a large number of keys, and unsatisfactory imaging effect of complex amplitude images. To solve these problems, a single-pixel complex-amplitude imaging encryption scheme based on random orthogonal modulation is proposed in this paper. The scheme realizes complex complex-amplitude object imaging by using orthogonal complex matrix inversion, and at the same time uses two random integer sequences as keys to scramble the orthogonal complex matrix to realize the encryption of the original images. This not only enhances the security of the system but also greatly reduces the number of transmitted keys. Subsequent simulation experiments verify the feasibility and security of the scheme, and the scheme can resist some common noise interference and show good robustness.
Keywords: image encryption; complex amplitude imaging; orthogonal matrix; random modulation
0" 引" 言
随着互联网技术的不断发展,网络中的数据交互日益频繁,个人隐私、商业机密、医疗等各个领域的信息都在通过网络传输。互联网已经被广泛应用于卫生、教育、银行、国防等众多领域。然而,任何信息在传输过程中都可能受到不法分子的网络攻击,导致信息泄露,严重时甚至可能危害国家安全和社会稳定。因此,如何保障网络传输中的信息安全显得尤为重要。
在网络中,我们经常使用的信息包括文本信息、音频信息、图像和视频信息。其中,图像作为一种重要的信息载体,其传输安全尤为重要。目前,常见的图像加密方式分为光学图像加密和数字图像加密。光学图像加密技术主要通过光学变换的方法,将照明图案的光场信息(如振幅和相位信息)隐藏起来,从而保证图像在传输中的安全性。数字图像加密则是通过计算机或特定算法改变明文图像中像素的位置和值,使图像失去原始信息,从而成为密文。这样,即使攻击者获得密文图像,也无法获取有用的原始图像信息。近年来,光学图像加密技术因其高速并行、大容量、设计自由度高、复杂度高以及能够与数字图像加密技术联合使用等特点,受到了越来越多学者的关注和研究。
单像素成像,又称为关联成像或鬼成像(Ghost Imaging, GI),是一种基于量子光源实现非定域性成像的典型成像系统。最初,人们采用量子纠缠光源来完成成像实验[1],后来的研究证实,使用经典光源同样可以完成成像实验[2]。经过几十年的发展,单像素成像经历了从量子鬼成像到经典鬼成像,再到计算鬼成像(Computational Ghost Imaging, CGI)[3]的历史发展过程。2015年,Zhao等人[4]提出了一种基于二维快速反应码的关联成像光学加密方案,该方案在保证解密图像质量的同时,提高了信息的安全性,对关联成像技术在光学加密方面的发展起到了很大的促进作用。2016年,Wu等人[5]提出了一种基于计算鬼成像的多图像加密方案。该方案利用不同衍射距离的计算鬼成像,将每幅平面图像加密成一个强度向量,最终通过将所有强度向量叠加形成密文,从而实现了多图像加密。2019年,Yuan等人[6]提出了一种基于Hadamard矩阵和空间复用的多图像加密方案。该方案通过对原始图像的像素进行升序重排以及空间复用技术,实现了对多幅图像的同时加密。2020年,刘等人[7]提出了一种基于超混沌及压缩感知的计算鬼成像加密方案。该方案通过DNA操作扩散,利用超混沌系统生成的伪随机序列获得相位掩膜序列,并以此作为加密密钥。2022年,蒋等人提出了一种基于RSA公钥加密的单像素图像加密方案[8],该方案利用两组随机序列生成所需的调制模板,并将其投影到秘密图像上,然后通过探测器获取密文信息。最后,通过RSA加密算法对随机序列进行加密,完成整个加密过程。
上述加密方案存在一些不足。从加密类型来看,这些方案大多数基于单像素成像且采用对称加密方式。然而,对于复杂的复振幅图像,其成像效果不够理想。因此,基于现有的单像素成像加密技术,本文提出了一种新的基于单像素复振幅成像的加密方案。该方案利用计算机生成两个随机整数序列,对正交复数矩阵进行行和列的置换,并通过两个相位掩膜将置乱后的复数矩阵调制成所需的正交复数矩阵散斑,投影到目标图像上。最终,光电探测器收集并处理这些散斑,获取目标图像的振幅和相位信息,并通过每次获取的振幅和相位信息重组成复数矩阵,再进行逆变换以重构目标图像。
该方法能够将两个随机序列作为加密密钥,实现对目标图像的加密,从而增强系统的安全性。在遭受常见的噪声攻击(如高斯噪声)时,重构出的复振幅图像仍能辨认出原始信息,展现出良好的鲁棒性,同时提高了加密效率。
1" 基本原理
1.1" 正交复数矩阵
本文采用基于哈达玛排序的共轭对称复数哈达玛变换[9](Conjugate Symmetric Natural Complex Hadamard Transform, CS-NCHT)生成复数矩阵。随后,对复数矩阵的行和列进行比特反转(Bit Reversal Conversion, BRC),以生成正交复数矩阵。其过程如下所示:
令hN表示一个N阶的复数矩阵,其中N=2n,且n为任意整数,则hN可表示成如下递归形式:
(1)
其中,SN/2、hN/2、hN/2可通过递归形式生成,其数学表达式为:
(2)
(3)
(4)
其中,IN/4表示单位矩阵,SN、hN/2以及hN/2的起始矩阵为:
(5)
其中,,另外式(4)中I N/4可表示为:
(6)
以8阶复数矩阵为例,根据式(1)可知:
(7)
则8阶复数矩阵可表示为:
(8)
将各个起始矩阵的值带入式(8)中得到8阶复数矩阵的值:
(9)
最终生成的矩阵是一个具有正交性质的复数矩阵,因此可以将其作为调制散斑用于单像素复振幅成像。
1.2" "随机向量
首先先生成两个包含整数随机排列的向量和作为加密密钥,密钥的长度可根据需要做出调整,以生成一个256×256大小的随机正交矩阵为例,首先生成两个含有1~64整数的随机向量,然后随机向量和可通过以下计算式生成:
(10)
1.3" 单像素复振幅成像方案
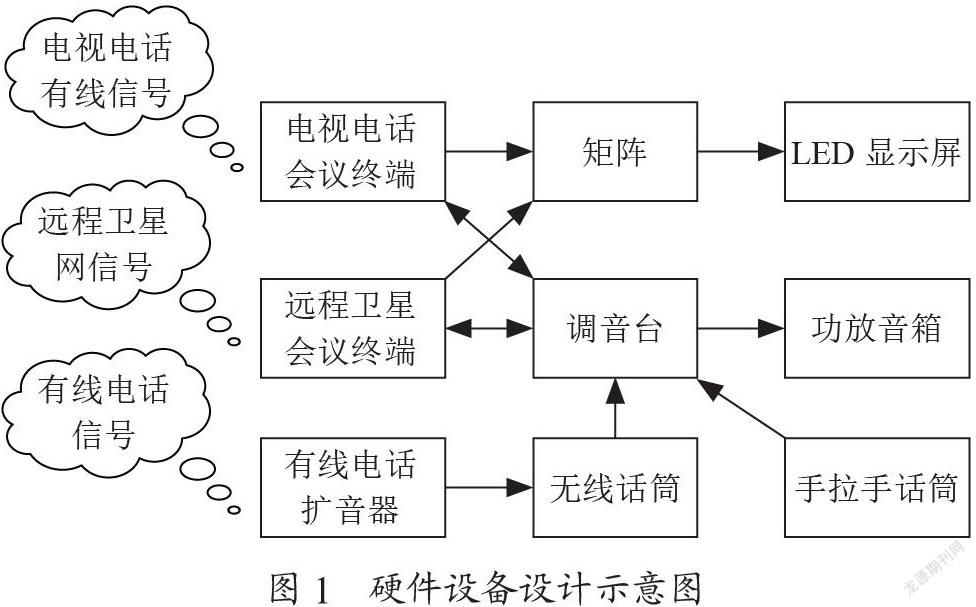
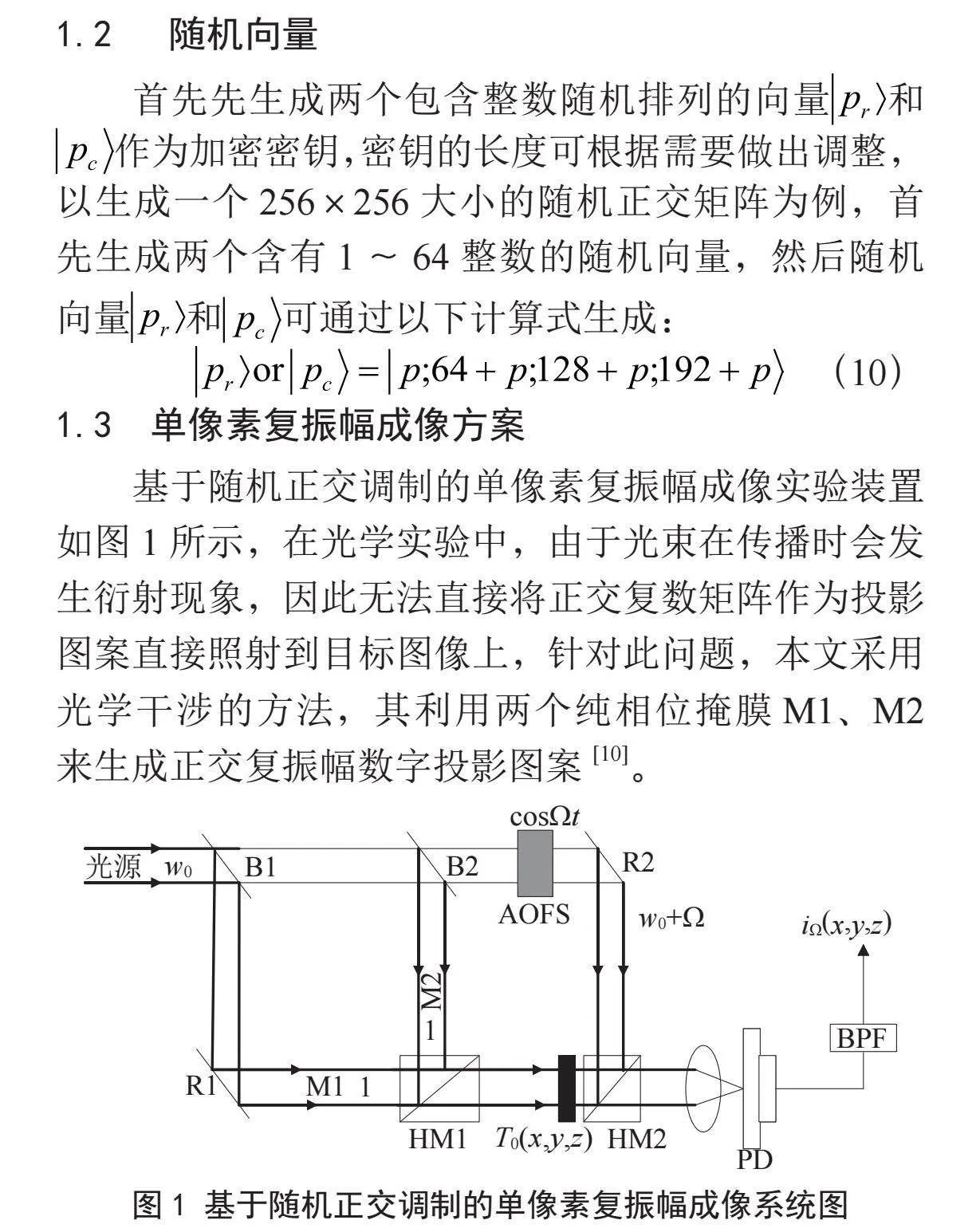
基于随机正交调制的单像素复振幅成像实验装置如图1所示,在光学实验中,由于光束在传播时会发生衍射现象,因此无法直接将正交复数矩阵作为投影图案直接照射到目标图像上,针对此问题,本文采用光学干涉的方法,其利用两个纯相位掩膜M1、M2来生成正交复振幅数字投影图案[10]。
首先,激光器光源发出的频率为ω0的光束,经过分术镜B1、B2以及反射镜R1之后,分别照射在两个纯相位掩模M1和M2上,经过M1和M2相位调制后,两束光由半透明反射镜(HM1)组合在一起,在输出平面处彼此干涉生成需要被投影的正交复数矩阵图案,其中两个相位掩膜到输出平面的距离必须相同(假设距离为1)。将通过干涉的方法生成的正交复数矩阵投影散斑照射到目标图像上,经目标物体反射或散射的光信号与另一处分经过分束镜B1、B2以及反射镜R2且被被频率为ω0+ Ω的声光调制器(Acousto-Optic Modulator, AOM)调制过的参考光束P1在目标图像后面的另一个半透明反射镜(HM2)中组合在一起形成新的干涉光信号P,新的干涉光束经过透镜聚集后被放在后面的光电探测器(Photodetector, PH)收集。
假设目标图像图像T(x,y,z)的大小为p×p,生成的复数正交矩阵大小为M×N,且N=p×p,因此,当全部采样完成后,计算机收集的所有探测结果可以写成如下数学形式:
其中,d表示计算机收集的探测结果,H表示正交复数矩阵,T表示经过变换后的待重构的复振幅图像矩阵。由于使用的复数矩阵散斑具有正交性,因此理论上可以通过逆矩阵变换的方法来重构复振幅图像:
其中,表示重建的目标图像,H表示复数正交基图案的逆矩阵,η表示一个常数。
2" 实验仿真与分析
2.1" 实验仿真
为了验证所提方案的可行性,本文在计算机上使用MATLAB 2021a软件进行了多次仿真测试。实验中采用两幅64×64像素大小的图像,分别是学校英文简称“NCWU”(图2(a))和“C”(图2(b)),分别作为复振幅图像的振幅和相位,从而构成原始复振幅秘密图像。根据本文1.1节提出的方法,利用计算机生成一个4 096×4 096的正交复数矩阵。然后,通过两个随机序列对正交复数矩阵的行和列进行置乱,得到一个随机的正交复数矩阵(如图2(c)所示)。这两个随机序列是在MATLAB 2021a软件中通过随机函数及式(2)生成的。具体步骤如下:首先,利用软件生成两个数值范围在[1,256]的随机整数序列(图2(d)、图2(e)),再利用式(2)将这两个序列的随机分布扩展到区间[1,4 096]。从图中可以看出,随机整数的分布散乱无序,具有良好的加密特性。接下来,利用两个纯相位掩膜干涉(图2(f)、图2(g))的方法,将随机正交复数矩阵的每一行重组成投影散斑,并依次投影到目标图像上。与参考光束信号重组后,信号被光电探测器收集。将收集到的结果经过一系列处理(包括外差频率滤波)后得到检测序列,并将所有检测结果排列成64×64的矩阵形式,最终得到密文,结果如图2(h)所示。
接收方利用从私人信道传输过来的随机整数序列密钥重新生成随机正交复数矩阵图案,采用逆矩阵变换的方法对从公共信道传输过来的加密图像进行解密。解密结果如图2(i)和(j)所示。从解密结果中可以看出,解密图像依旧能够清晰地还原原始图像信息。
2.2" 加密特性
在本节所提到的单像素复振幅成像方案中,投影散斑是通过两个随机整数序列生成的,具有一定的加密功能。该方案将两个随机序列作为加密密钥,用户只有获得正确的加密密钥,才能通过逆矩阵的方法重构秘密图像。
2.2.1" 加密流程
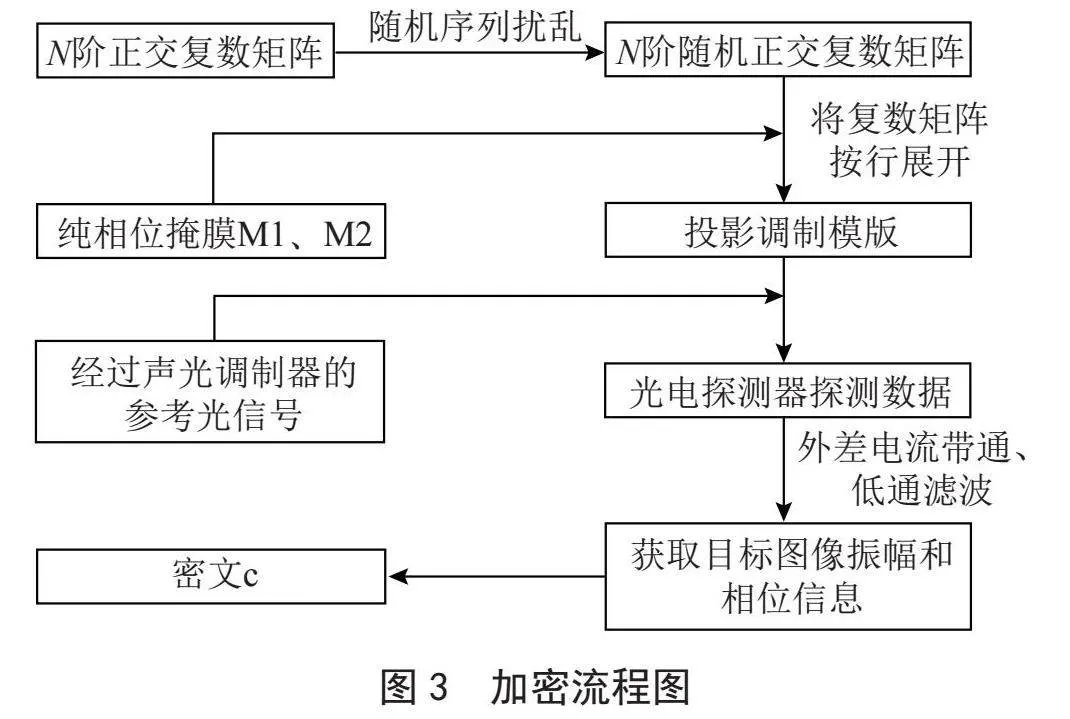
加密流程图如图3所示,具体加密过程如下:
1)采用本文1.1小节提出的方法生成一个N阶的正交复数矩阵HN,有正交矩阵的性质可知,HN满足如下数学关系式:
(14)
其中,E表示N阶单位矩阵。
2)通过计算机生成两个随机整数向量和,两个序列的长度大小可根据实际复振幅图像的大小来设置,假设对一个64×64像素大小的复振幅图像进行单像素成像及加密,则需要一个4 096×4 096大小的正交复数矩阵,那么可以生成两个分别含有1至64整数的随机序列并将其作为加密密钥,然后通过式(2)来获得随机向量和,将两个随机向量里面的元素值分别作为矩阵的行数和列数对正交复数矩阵HN的行和列进行置乱,得到杂乱无序的随机正交复数矩阵H。
3)将随机正交复数矩阵H的每一行进行展开,展开后的每一行重新组合成复数矩阵Hi的形式,并采用两个纯相位掩膜干涉的方法生成投影调制散斑Hi照射到目标图像上,经过目标物体反射和散射的光与另一光路经过声光调制器调制的参考光信号相干涉并被光电探测器收集完成一次采样,这样的采样过程需要4 096次。
4)将光电探测器每次收集的数据结果利用外差电流带通、低通滤波的方法来获取每次探测到的目标图像的振幅和相位信息di,最终将所有的di重新排列成64×64复数矩阵,即密文。
5)将密文通过公共信道传输给接收方,同时将密钥通过私人信道传输给接收方,即完成整个加密过程。
2.2.2" 解密流程
秘密图像的加密过程是加密的逆过程,其详细过程如下所示:
1)接收者这边利用通过私人信道获得密钥将正交复数矩阵的行和列进行重新排列,重新生成随机正交复数矩阵H。
3)将通过公共信道获得的密文数据利用逆矩阵变换就可以将秘密图像进行解密。
其中,T 表示解密后的复振幅图像,H 表示随机正交复数矩阵的转置矩阵,η表示常数。
2.3" 性能分析
2.3.1" 安全性分析
安全性是加密系统的一个重要评价标准。在本节所提出的加密方案中,两个随机整数向量密钥均为加密密钥的一部分。如果攻击者使用其中的一个或两个错误的密钥对加密图像进行解密,且无法从解密图像中获取原始图像信息,则证明该系统具有较高的安全性。图4展示了使用错误行序列密钥、错误列序列密钥以及行列序列均错误的密钥进行解密的振幅和相位结果。从解密结果可以看出,无论哪种序列出现错误,都无法还原秘密图像。
2.3.2" 鲁棒性分析
为了验证加密系统的鲁棒性,本文还模拟测试了密文的1/16 图像像素被破坏(图5(a))以及在密文上加入方差为 0.01和均值为0的高斯白噪声(图5(d))的解密情况,如图5(b)、(c)、(e)、(f)所示分别为两种情况的解密结果,其解密结果的峰值信噪比分别为19.577 3 dB、13.425 6 dB、16.325 8 dB、12.623 8 dB。从解密结果中可以看出,当密文存在一定的破坏以及包含一定的高斯噪声时,虽然质量有所下降但依然能够重建秘密图像。
为了验证加密系统的鲁棒性,本文模拟测试了两种情况:一是密文的1/16图像像素被破坏(图5(a)),二是密文上加入方差为0.01、均值为0的高斯白噪声(图5(d))。解密结果如图5(b)、(c)、(e)、(f)所示,其对应的峰值信噪比分别为19.577 3 dB、13.425 6 dB、16.325 8 dB、12.623 8 dB。从解密结果可以看出,当密文存在一定程度的破坏或包含高斯噪声时,虽然解密图像质量有所下降,但依然能够重建秘密图像。
3" 结" 论
本文提出了一种基于随机正交调制的单像素复振幅成像加密方案。该方案利用正交复数矩阵的逆变换方法,实现了复杂复振幅物体的成像。同时,通过两个随机整数序列作为密钥来扰乱正交复数矩阵,从而实现对原始图像的加密。这不仅增强了系统的安全性,还显著减少了密钥的传输量。后续的仿真实验证明,该方案能够有效抵御常见的噪声干扰,具有良好的鲁棒性,从而验证了其可行性和安全性。
参考文献:
[1] STREKALOV D V,SERGIENKO A V,KLYSHKO D N. Observation of Two-Photon “Ghost” Interference and Diffraction [J/OL].Physical Review Letters,1995,74:3600[2024-10-16].https://doi.org/10.1103/PhysRevLett.74.3600.
[2] ERKMEN B I,SHAPIRO J H. Ghost Imaging: From Quantum to Classical to Computational [J].Advances in Optics and Photonics,2010,2(4):405-450.
[3] SHAPIRO J H. Computational Ghost Imaging [J/OL].Physical Review A,2008,78:061802[2024-10-20].https://doi.org/10.1103/PhysRevA.78.061802.
[4] ZHAO S M,WANG L,LIANG W Q,et al. High Performance Optical Encryption Based on Computational Ghost Imaging with QR Code and Compressive Sensing Technique [J].Optics Communications,2015,353:90-95.
[5] WU J J,XIE Z W,LIU Z J,et al. Multiple-Image Encryption Based on Computational Ghost Imaging [J].Optics Communications,2016,359:38-43.
[6] YUAN X,ZHANG L H,CHEN J,et al. Multiple-Image Encryption Scheme Based on Ghost Imaging of Hadamard Matrix and Spatial Multiplexing [J].Applied Physics B: Lasers amp; Optics,2019,125(9):1-13.
[7] 刘芳. 基于超混沌及压缩感知的计算鬼成像加密方案研究 [D].长沙:湖南大学,2020.
[8] 蒋新竹,袁胜.基于单像素成像和公钥密码的图像加密技术 [J].电力信息与通信技术,2022,20(5):87-94.
[9] AUNG A,NG B P,RAHARDJA S. Conjugate Symmetric Sequency-Ordered Complex Hadamard Transform [J].IEEE Transactions on Signal Processing,2009,57(7):2582-2593.
[10] ZHANG Y,WANG B. Optical Image Encryption Based on Interference [J].Optics Letters,2008,33(21):2443-2445.
作者简介:张恒(1998—),男,汉族,河南商丘人,硕士研究生在读,研究方向:信息安全。