

摘" 要:风能作为一种可再生清洁能源,得到了高速发展。高精度的风力发电量预测可为电力调度以及平抑并网波动提供重要依据。文章基于ARIMA模型,分别进行超短期、短期和中长期风力发电量预测,探讨其可行性和有效性。使用某风电场2019年1月1日至2020年12月31日的风电功率数据进行建模,并开展不同时间长度的预测。在此基础上,考虑数据的周期性特征以及实际气候因素对发电功率的影响,优化模型的预测效果。实验结果表明,考虑数据周期性与外生变量的影响能够显著提升对实际功率的预测精度。超短期、短期和中长期预测的均方根误差分别为7.16、12.63和17.98。
关键词:风力发电;发电量预测;ARIMA;皮尔逊系数
中图分类号:TP39;TM614 文献标识码:A 文章编号:2096-4706(2025)04-0157-06
Power Generation Forecasting of Wind-generated Electricity Based on ARIMA
LIU Jixiong1, ZOU Rui2, XU Siwei2
(1.Wuhan Electric Apparatus Research Institute Co., Ltd., Wuhan" 430050, China; 2.Hubei University, Wuhan" 430062, China)
Abstract: Wind energy, as a renewable and clean energy source, is developing at a high speed. High-precision wind power generation forecasting can provide an important basis for power dispatching and mitigating grid-connection fluctuations. Based on the ARIMA model, this paper conducts ultra-short-term, short-term, and medium-to-long-term wind power generation forecasts to explore its feasibility and effectiveness. The wind power data of a wind farm from January 1, 2019 to December 31, 2020 is used for modeling and forecasting over different time lengths. On this basis, considering the periodic characteristics of the data and the influence of actual climate factors on power generation, the forecasting effect of the model is optimized. The experimental results show that considering the influence of periodic data and exogenous variables can significantly improve the forecasting accuracy of actual power. The RMSE of ultra-short-term, short-term, and medium-to-long-term forecasts are 7.16, 12.63 and 17.98, respectively.
Keywords: wind power generation; power generation forecasting; ARIMA; Pearson correlation coefficient
0" 引" 言
随着全球对清洁能源的需求不断增长,风力发电作为一种可再生、清洁且环保的能源形式,越来越受到人们的关注和重视。风力发电通过将风能转化为电能,为能源行业提供了一种可持续发展的解决方案[1]。然而,与其他形式的能源相比,风力发电的特点之一是其波动性和不确定性,风速的随机波动、气象条件的变化以及地理位置的差异都会导致风力发电量的波动。风力发电功率预测即利用当前的信息对未来一段时间的风电功率大小进行预测,这对于风电场的运营规划和管理,以及电力的调度与系统的维护至关重要[2]。
预测风力发电量的准确性直接影响到风电场的经济效益和电网运行的稳定性。在实际生产中,精准的风力发电量预测可以帮助电网管理者合理安排发电计划、调配电力资源,避免供需不平衡引发的电力负荷问题。此外,对风力发电量的准确预测还有助于降低电力系统的运营成本,并优化电力市场的运行。
针对风电的预测方法,国内外已有诸多研究。学者们对于用风电发电量的预测方法大致分为两大类:基于时间序列模型的预测方法和基于机器学习的预测方法。时间序列是指一组在连续时间上测得的数,可分为单变量时间序列和多变量时间序列[3]。基于时间序列模型的预测方法主要包括自回归移动平均模型(Autoregressive Integrated Moving Average, ARIMA)、自回归条件异方差模型(Autoregressive Conditional Heteroskedasticity, ARCH)、广义自回归条件异方差模型(GARCH)等。曹俊波[4]等运用ARIMA模型进行风功率预测,提出一种确定最优差分次数的方法对模型进行优化。机器学习方法通过对大量数据的学习和模式识别,能够更灵活地适应不同的数据特征,并在一定程度上提高预测的准确性。向勇[5]等将深度学习引入了循环神经网络,进行大规模风电功率的预测,发现组合模型明显降低了预测的相对误差。李相俊[6]等采用LSTM(Long Short Term Memory)算法进行风电功率预测,发现对于各季节的周发电功率与日发电功率都表现良好。部分学者还针对不同的时间尺度进行了深入的研究。
风功率预测从时间尺度上可以分为3类:超短期预测(时/分/秒)、短期预测(时/天)、中长期预测(天/周/月/季)。超短期预测通常是指0到4小时的风力发电量预测,主要用于电力系统实时调整。韩朋[7]等使用深度学习框架,结合LSTM与注意力模型,预测未来4小时的风电功率。短期预测是指预测未来0到72小时的风电功率,主要用于拟定发电计划,通常需要考虑风速、风向等气象条件。余铮[8]等对原始风电数据进行分解,得到低频、中频、高频和趋势特征,对高频采用LSTM进行预测,其余选择支持向量机的方法,最终得到短期风电预测结果。中长期预测通常是三天到数周的功率预测及月度、年度的电量预测,中期预测主要用于对机组组合优化、常规电源开机计划制订、海上风电检修,长期预测主要用于年、月电量平衡及制订燃料计划等。对于中长期的风电预测,由于数据的时间尺度较大,学者们多使用非线性学习能力较强的模型,陈子含[2]等在进行中长期风功率预测时,搭建图卷积神经网络模型,并采用差分拟合降低模型拟合难度,使用粒子群优化算法优化整体目标函数。何健伟[9]等结合LSTM与RF(Random Forest)进行中期发电功率预测,RF用于修正短期误差,有效提升了中长期预测精度。
风力发电功率预测目前已取得不少研究成果,但大多数文献只选择一种时间尺度进行预测,并且在基于时间序列的预测方法中,仅考虑了发电功率的单一变量。本文将着重介绍利用ARIMA模型进行风力发电量预测的方法,在此基础上考虑风电功率的周期性以及影响风电功率的外生变量,分别构建SARIMA和SARIMAX模型,探究是否提高预测精度。并根据实际应用的需要,将基于ARIMA模型的预测分为超短期、短期和中长期。对比分析模型在超短期,短期,中期以及长期预测的效果,为不同的应用提供合适预测方法,以促进风电场的可持续发展和电力系统的稳定运行。
1" 理论介绍
1.1" ARIMA
ARIMA(自回归积分移动平均)是一种经典的时间序列分析方法,用于预测未来的数据。ARIMA模型结合了自回归(AR)模型、差分(I)和移动平均(MA)模型的特性。ARIMA模型的基本原理如式(1)所示:
ARIMA(p,d,q)=AR(p)+I(d)+MA(q)" " (1)
其中,AR(p)表示自回归模型,I(d)表示差分模型,MA(q)表示移动平均模型。
自回归(AR):ARIMA模型基于自回归,即当前时间点的值与前面若干时间点的值有关,即回归的阶数。自回归阶数p表示当前时间点与前面p个时间点的值有关。
差分(I):为了消除时间序列数据的非平稳性,ARIMA模型通常需要进行差分操作,即将原始数据转化为差分数据,消除趋势和季节性等影响。差分阶数d表示需要对时间序列数据进行差分的次数。
移动平均(MA):ARIMA模型基于移动平均,即当前时间点的值与前面若干时间点的误差有关,即移动平均的阶数。移动平均阶数q表示当前时间点与前面q个时间点的误差有关。
ARIMA模型的核心思想是通过对时间序列数据进行差分操作,将非平稳的时间序列转化为平稳的时间序列,然后利用自回归和移动平均的组合来捕捉数据的自相关性和移动平均性。它可以通过对时间序列数据进行分析和拟合,估计出合适的模型参数,从而进行数据预测和建模。
1.2" SARIMA
SARIMA在ARIMA的基础上考虑了季节性因素[10],能够有效捕捉趋势与周期性变化。
假设{Xt}是一个时间序列,x1,x2…xn为n个有序观测值。B是滞后算子,用于表示序列的滞后关系,式(2)表示t时间点的观测值xt经过B的作用后,得到t-1时间点的观测值xt-1。
B·xt = t-1" " " " " " " " " " " " " " "(2)
非平稳的时间序列通常要进行差分运算,计算当前观测值与前一个观测值之差,以消除数据的非平稳性。时间序列的d阶差分可以表示为:
(3)
当数据每隔s个时间点就呈现出相似特征时,就可以认为其存在周期性。s表示季节性的周期长度,季节性差分算子表示为式(4):
(4)
SARIMA模型中自回归描述变量与自身在不同时间点的相关关系,自回归算子可表示为式(5),模型可以表示为式(6)。其中εt表示误差项,ϕ表示每个滞后值的权重。
(5)
(6)
移动平均描述当前观测值与过去随机误差之间的关系,用过去q个时期的随机误差来线性表达当前的预测值。令q阶移动平均算子为式(7),则移动平均模型可以表示为式(8),其中θ表示权重。
(7)
(8)
季节性自回归差分移动平均模型可以记为SARIMA(p,d,q)×(P,D,Q)s,模型的结构表示为式(9):
(9)
1.3" 评价指标
对于文中风力发电量预测的实例,为对模型性能进行客观的判断,本文选择的评价指标是平均绝对误差(MAE)和均方根误差(RMSE),这些指标可以直观地反映模型预测的准确性,适用于连续数值型数据的评估。其公式分别为(10)和(11):
(10)
(11)
2" 算例分析
2.1" 数据及实验方法
文中数据为某风电场的数据集,涵盖了该风电场在2019年1月1日至2020年12月31日期间的运行数据,采样间隔为15分钟,该数据集包含了多个特征。
天气特征包括:10米高度处风速(m/s),10米高度处风向(°),30米高度处风速(m/s),30米高度处风向(°),50米高度处风速(m/s),50米高度处风向(°),70米高度处风速(m/s),70米高度处风向(°),气温(℃),气压(hPa),相对湿度(%)等。这些特征提供了风力发电的关键环境因素,可以帮助理解和预测风力发电量的变化。其中,风速和风向是最直接影响风力发电量的因素,而气温、气压和相对湿度等气象因素也可能对风力发电产生一定影响。
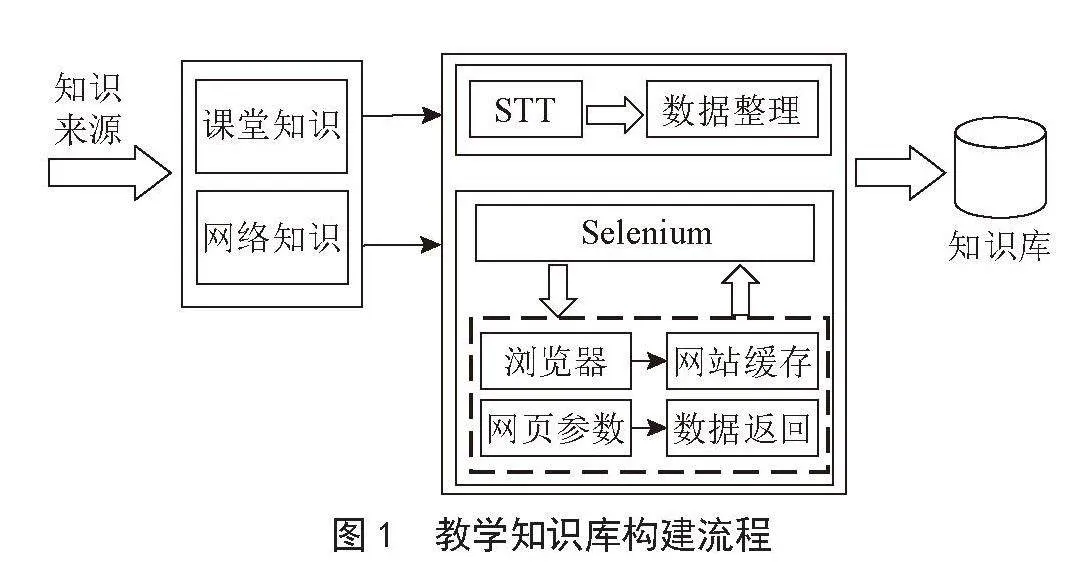
为准确预测风力发电量,对于数据集中的大量数据,通过可视化了解其基本特征,筛选出对发电量有显著影响的外生变量,并将数据划分为训练集和测试集,分别构建ARIMA、SARIMA和SARIMAX模型。为了更清晰地展示实验方法的具体步骤,建模流程如图1所示。
2.2" 数据预处理
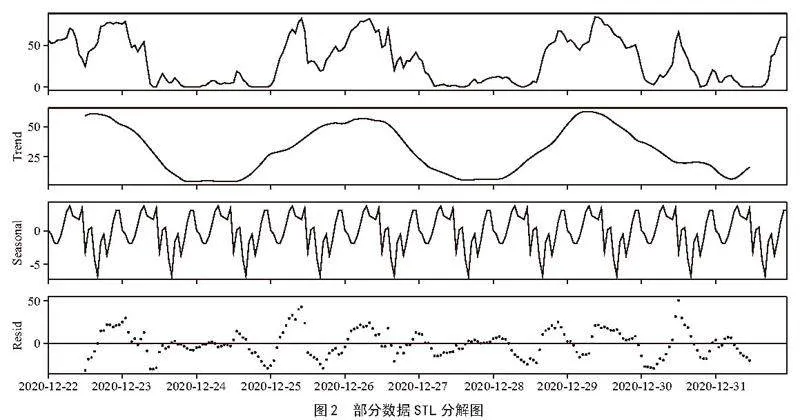
在建立模型之前,观察原始数据,发现每天的实际发电功率均存在较大波动,且波动趋势相似。为验证数据是否存在周期性,本文对序列进行基于加权回归的季节趋势(seasonal-trend decomposition using Loess, STL)分解,由于数据集中的“实际功率”包含负值,此处使用加法模型分解数据,即原始数据由趋势、周期和残差三个部分相加组成:
原始数据 = 趋势+周期+残差" " " " (12)
发现风电功率数据的周期是以天为单位的,每天采样的数据具有96个时间点,即周期S = 96。由于训练设备的算力限制,对于此类较长的周期难以添加到模型当中进行运算,因此对原始数据进行聚合,通过取平均值的方式将原始数据的多个时间点聚合为整点时间的数据,转换为较高层次的时间间隔。经处理后的数据每天有24个采样点,再次进行STL分解,展示部分数据的分解结果如图2所示,此时的数据以24小时为周期,即S = 24,利于进一步进行时间序列的分析。
2.3" 相关性分析
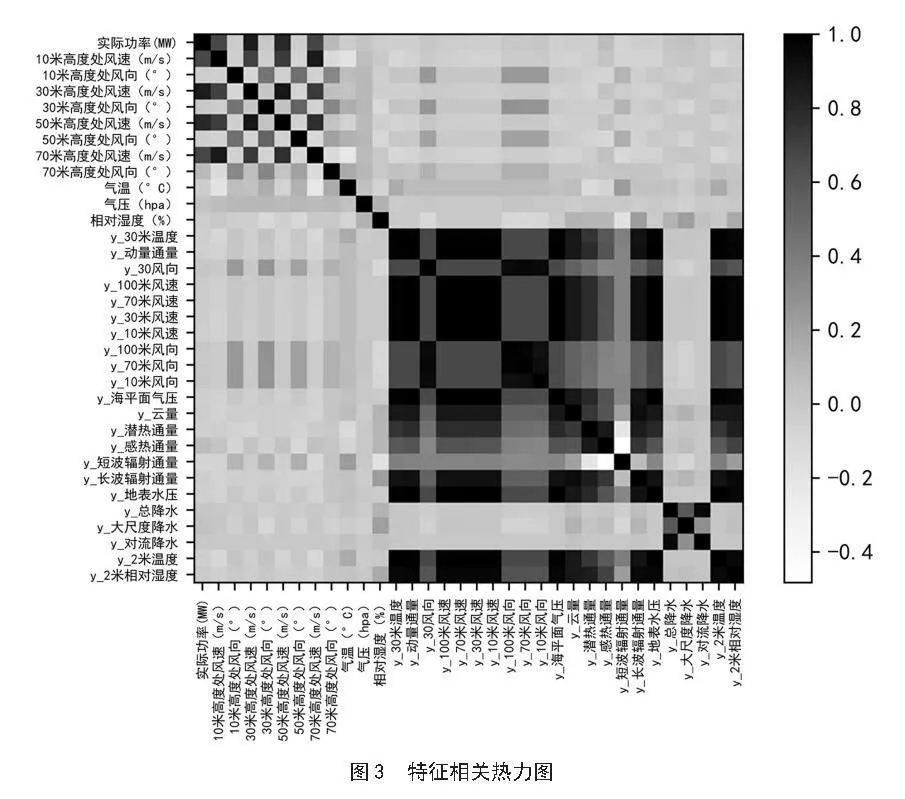
在实际的情境中,风电功率与风向、风速以及各种气候因素之间有着较为紧密的相关性,在进行预测时,将高相关性变量的输入到模型当中可以提高预测精度,而低相关性的数据往往会干扰训练过程,影响模型预测效果。为了筛选出合适的特征,此处进行相关性分析。
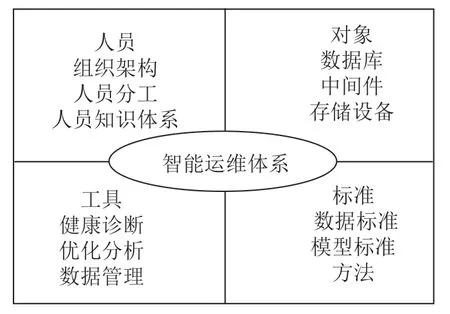
皮尔逊系数(Pearson correlation coefficient)是一种衡量两个连续变量之间线性关系强度和方向的统计量,通常用符号“r”表示。其计算公式如式(13)所示,xi和yi分别表示第i个观测值的两个变量,和分别表示两个变量的均值,n表示观测值的数量。
(13)
皮尔逊相关系数的取值范围在-1到1之间,其值的大小表示了线性相关程度的强弱,越接近于1或-1表示相关性越强,当相关系数r大于0.8时,认为变量间有极强的相关性[11]。为了更直观的表示各特征值之间的相关性关系,采用热力图可视化相关性,如图3所示。
通过相关性分析结果可得,与风电功率相关程度最高的气候特征为风速,其中30米高度处风速的相关系数为0.88,具有极强的相关性,其次以此为50米高度处风速、10米高度处风速和70米高度处风速。不同高度处风速之间存在着较强的正相关性,为简化输入到训练模型的特征数量,避免特征冗余,将30米高度处风速作为外生变量加入模型进行进一步的训练。
2.4" 模型构建
本研究对风电功率进行超短期、短期和中长期预测,分别选择4 h、24 h、72 h作为预测长度。由于原始数据集的数据量巨大,共包含17 524条数据,不适合直接应用于ARIMA模型进行训练,因此在确定训练集的样本数时,按照10:1的比例确定数据量用于模型拟合,例如短期预测取40个时间步长的数据输入模型,得到未来4小时数据的输出。在模型的选择上,本文基于ARIMA模型进行预测,并利用数据的周期性特征以及引入外生变量对模型进行优化,构建SARIMAX模型,此处主要说明SARIMAX模型的构建过程。
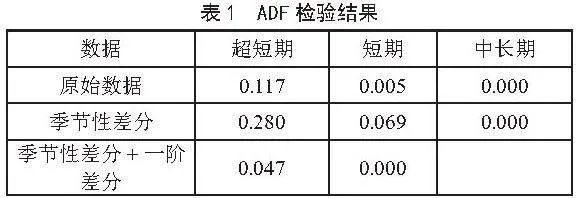
建模初期,首先需要检验数据的平稳性。分别对用于不同时间长度预测的数据进行ADF检验,并通过差分消除其周期性与趋势,结果如表1所示。通过平稳性检验结果,可以确定在用于建模的数据分别需要的差分次数。
在建模前,还需要验证已平稳的数据是否为白噪声。使用Ljung-Box检验法,检验发现已处理平稳的序列不是白噪声序列,可用于建模分析。
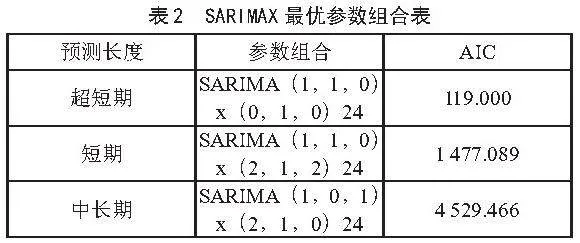
模型定阶为建模的重要环节,将训练集的数据与外生变量数据同时输入模型,采用网格搜索法的方式遍历参数组合,确定模型的最优参数,以赤池信息准则(AIC)作初步判断依据,统计量越小,表示模型的性能越好。对AIC较小的几个参数组合不断筛选与调整,最终确定的模型参数如表2所示,可用于预测。
3" 预测结果对比
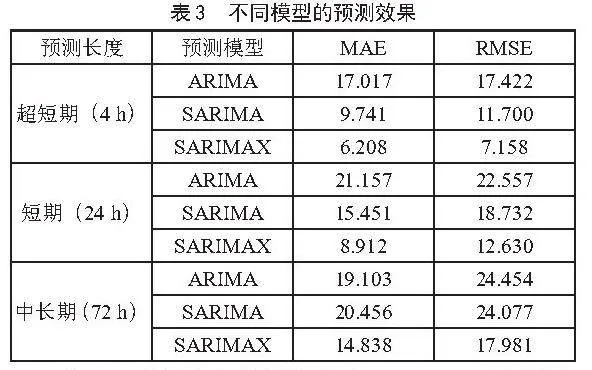
分别运用ARIMA、SARIMA、SARIMAX模型进行超短期、短期和中长期风电预测。其中,ARIMA模型使用风电场历史发电功率数据进行预测,SARIMA模型考虑了数据的周期性特征,SARIMAX模型在捕捉数据周期性的基础上,考虑了风速对于实际发电功率的影响。汇总模型的预测效果如表3所示,此处采用MAE和RMSE作为模型的评价指标。
从表3的对比结果可以看出,ARIMA模型更适用于较少时间步的预测,对于超短期风电功率预测的平均绝对误差和均方根误差都相对较低。考虑数据的周期性能够在一定程度上提升预测精度,对比ARIMA模型,超短期和短期预测的MAE分别降低了42.7%和27.0%。风速对于发电功率也有着较大影响,当添加风速作为外生变量以后,超短期、短期和中长期的预测效果都明显提升,超短期预测的RMSE为7.16,验证了优化后的ARIMA模型能够提升功率的预测准确度。
4" 结" 论
本文基于ARIMA模型分别对风力发电功率进行超短期、短期以及中长期的预测,在观察模型对于不同时间长度的数据预测效果的基础上,考虑了数据的周期性与外生变量的影响性,优化ARIMA模型。实验发现考虑周期性和外生变量能够显著提升预测精度。
参考文献:
[1] 杨乘胜.面向新建风电场的短期风电预测方法 [J].中国科技信息,2022(19):104-106.
[2] 陈子含,滕伟,胥学峰,等.基于图卷积网络和风速差分拟合的中长期风功率预测 [J].中国电力,2023,56(10):96-105.
[3] 陈孝文,苏攀,吴彬溶,等.基于改进长短期记忆网络的时间序列预测研究 [J].武汉理工大学学报:信息与管理工程版,2022,44(3):487-494+499.
[4] 曹俊波,周任军,邓学华,等.考虑优化ARIMA模型差分次数的风功率预测 [J].电力系统及其自动化学报,2019,31(1):105-111.
[5] 向勇,王一军,孔寅恪.基于深度循环神经网络的大规模风力发电功率预测 [J].资源信息与工程,2021,36(2):136-139.
[6] 李相俊,许格健.基于长短期记忆神经网络的风力发电功率预测方法 [J].发电技术,2019,40(5):426-433.
[7] 韩朋,张晓琳,张飞,等.基于AM-LSTM模型的超短期风电功率预测 [J].科学技术与工程,2020,20(21):8594-8600.
[8] 余铮,金波,焦尧毅,等.基于混合深度学习的短期风电预测研究 [J].武汉理工大学学报:信息与管理工程版,2024,46(1):170-174.
[9] 何健伟,曹渝昆.LSTM-RF的中长期风电功率组合预测方法 [J].上海电力大学学报,2020,36(4):341–350.
[10] 丁锐,李伟,王若舟.基于SARIMA和LSTM组合预测模型 [J].计算机与数字工程,2020,48(2):304-307+337.
[11] 程杰,陈鼎,李春,等.基于GWO-CNN-BiLSTM的超短期风电预测 [J].科学技术与工程,2023,23(35):15091-15099.
作者简介:刘吉雄(1971—),男,汉族,湖北荆州人,工程师,本科,研究方向:风机空气性能;邹瑞(1999—),女,汉族,陕西宝鸡人,硕士,研究方向:数据分析、数据挖掘;许思为(1999—),男,汉族,湖北天门人,硕士,研究方向:数据挖掘、机器学习。
收稿日期:2024-07-24