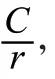



摘" 要:黄金是一种特殊的金融商品,具有避险功能。黄金期货价格受多方面因素的影响,一般认为黄金期货价格变化趋势呈现非线性非平稳的时间序列,传统的预测模型难以对其进行有效的预测。文章向传统在线学习算法中加入信息传递,提出基于RNN的在线学习算法ROA(RNN-based Online Algorithm);选用芝加哥商品交易所黄金期货价格数据进行实证分析,使用CNN-LSTM作为基础预测模型,以MAE、RMSE、R2作为评价指标,结果表明在所有评价指标中ROA的预测性能均优于传统在线学习算法。
关键词:RNN;黄金期货价格;在线学习算法
中图分类号:TP39;TP183 文献标识码:A 文章编号:2096-4706(2024)11-0141-05
Prediction of Gold Future Prices Using CNN-LSTM Model under RNN Online Learning Framework
SHI Yansong1, YANG Bo1,2
(1.School of Mathematics, Yunnan Normal University, Kunming" 650500, China; 2.Yunnan Key Laboratory of Modern Analytical Mathematics and Applications, Yunnan Normal University, Kunming" 650500, China)
Abstract: Gold is a special financial commodity with a safe-haven function. The price of gold futures is affected by many factors and is generally regarded as a non-linear and non-stationary time series, which is difficult to be predicted by traditional forecasting models. We introduce information transmission into traditional online learning algorithms and proposes an online learning algorithm ROA (RNN based Online Algorithm) based on RNN (Recurrent Neural Network). Empirical analysis is conducted using the Chicago Mercantile Exchange gold futures price data, with CNN-LSTM (Convolutional Neural Networks-Long Short Term Memory) as the basic prediction model and MAE (Mean Absolute Error), RMSE (Root Mean Square Error), and R2 as evaluation indicators. The results show that the predictive performance of ROA is superior to traditional online learning algorithms in all evaluation indicators.
Keywords: RNN; gold future price; online learning algorithm
0" 引" 言
黄金是一种具有货币和商品双重属性的特殊贵金属,因其拥有避险功能和对抗通货膨胀的能力,一直是投资的热点。其价格变化也直接决定了黄金投资者和生产者的价值行为,因此,找到可靠的黄金价格预测方法是十分必要的[1]。
对金融时间序列预测较常使用的模型为自回归移动平均模型(ARMA)[2]、广义自回归条件异方差性(GARCH)[3]等。除了经典的计量经济学时间序列预测方法外,决策树[4]、遗传算法[5]、支持向量机(SVM)[6]和其他机器学习方法也被应用于金融时间序列的预测[7]。面对非线性非平稳的金融时间序列数据,机器学习方法能够较好地描述各种高度非线性的变化,在量化投资、风险控制等方面表现优异[8]。
在机器学习领域,可以将机器学习算法分为在线学习算法和离线学习算法。以往在时间序列预测的研究中较多地使用了离线学习算法[9]。离线学习可以充分利用训练数据,通过多次的迭代和调整参数来优化模型的性能。离线学习的不足在于无法及时适应数据的变化,如果新的数据规律和训练数据规律有很大的差异,那么模型可能会失效,此时需要重新训练模型。因此,离线学习适合于数据变化规律稳定且不需要实时更新的场景,例如图像识别、语音识别、自然语言处理等。但固定参数的离线学习算法并不能很好地适应金融时间序列数据的变化,尤其是在数据产生的规律发生变化时这种不适应性表现得更为突出。
在线学习算法能够持续不断地接收数据,实时动态地更新模型,适合大规模和流式数据的处理,受到研究者的高度重视,是当前机器学习领域的研究热点[10]。由此,随着机器学习的发展,在线学习算法开始被大家所关注[11]。在线学习算法让模型一直处于学习状态,使模型的参数随着数据的更新而更新,解决了由于离线学习算法参数固定而导致模型不能适应新数据产生规律的问题。
传统的在线学习算法只是将模型的参数更新,将学习好的参数作为下一次模型学习的初始参数,在模型的每一次学习中并没有进行数据历史信息的传递。这时我们注意到RNN(Recurrent Neural Network)具有一定的记忆功能,可以传递过往的历史信息[12],这能帮助模型更好地处理序列数据,所以我们拟基于RNN的原理对传统在线学习算法进行改进得到ROA。
为了提升在线学习下模型对黄金期货的预测效果,我们在独立的模型学习中加入了信息传递,以帮助模型更好地学习,由此构建了ROA框架。使用CNN-LSTM(Convolutional Neural Networks-Long Short Term Memory)模型在ROA框架下对黄金期货价格进行预测。最后利用MAE、RMSE、R2来评价所提出的ROA框架。
1" 方法与原理
1.1" RNN神经网络
RNN是Elman等人提出的网络模型,RNN是一种能够处理序列数据的神经网络,RNN的出现解决了传统神经网络无法捕捉时间序列数据间顺序关系的局限性[12]。传统神经网络不能直接利用时间序列的历史信息,但现实中,很多时间序列数据(如金融时间序列数据)前后都是相互关联的。RNN具有记忆能力,能产生信息流,在面对时间序列数据时能有更好的预测效果。RNN结构图如图1所示,xt-1、xt和xt+1输入模型时,模型都为同一个,共用参数θ,通过计算每一个样本的损失函数Loss,再通过总误差LOSS对模型进行学习,得到最优参数θ*。
RNN在学习时,将前一时刻的信息It-1和当前时刻的输入xt一同输入到模型中得到输出 ,并将当前时刻的信息It传递到下一时刻使用,如图1所示。在同一次学习中,所有时刻的模型共享本次学习的参数θ,得到每一时刻的误差 ,基于总误差最小的原则" 对模型参数进行更新学习。这样的信息流使得RNN在面对时间序列数据时较传统神经网络拥有更好的效果。
1.2" 在线学习和离线学习
1.2.1" 离线学习
离线学习算法是一种机器学习中模型学习的方式[10],是指在有限的数据集上进行模型的训练和评估,然后再将模型应用于新的数据。从式(1)中可以看到,利用训练集Xtrain和测试集Xtest将模型训练好以后,得到最优参数θ*,模型训练好的参数将不再发生变化。之后在获取新的数据后进行预测。
(1)
1.2.2" 在线学习
当数据产生的规律发生变化时,学习后参数固定的离线学习方式,不容易适应变化后的数据。对于变化后的数据,模型需要重新更新参数以保证预测效果,因此在线学习被提出[10]。
(2)
结合图2,从式(2)中我们可以看到在线学习在数据不断到来的过程中,动态地更新模型。以之前学习得到的参数" 表示初始学习参数,在线学习通过最近的历史数据集Xt-1对模型进行学习,得到最优参数 ,然后进行预测,得到t时刻的预测值 。当产生新数据xt时,利用新数据xt对模型重新学习,对t+1时刻进行预测,得到预测值 ,如此循环往复。由此可以看出,在线学习具有实时性,可以快速适应新数据的特征变化。
传统在线学习将数据输入模型进行学习,模型学习好后进行预测,等出现新的数据后,模型重新学习,重新预测,如此循环往复。如图2所示,传统的在线学习将每一批样本集" 输入模型学习,其中每一个样本" 按时间顺序输入模型得到对应的损失函数 ,模型通过对总误差" 进行更新,在模型学习完毕后进行测试。但从图2可以看到模型在每个批次学习之间,只对模型参数θ进行传递,没有信息的传递,即不能捕捉数据的前后关联。此时考虑对模型引入信息流,让模型具有记忆性。
1.3" 在线学习算法ROA
RNN会将当前时刻的信息保存以便后续输出,也会将信息传递到下一时刻使用,解决了传统神经网络处理序列信息时的局限性。传统在线学习只是将模型的参数进行传递,将模型上一时刻学习好的参数作为下一时刻模型学习的初始参数,但没有考虑时间序列数据之间的相关性,没有进行信息的传递。利用RNN的信息传递机制,我们可以对在线学习进行改进,加入信息传递,对模型的输入加入信息I,把上一时刻的信息和当前时刻的数据作为模型下一时刻的输入,构建ROA,让模型拥有记忆性,如式(3)和图3所示。
(3)
从图3中可以看到,模型在每一次的学习过程中,将上一时刻信息It-1和当前时刻的数据xt输入到模型中,得到当前时刻的信息It和预测值 ,同时将当前信息It传递到下一时刻使用。在对数据的处理中,当前时刻模型学习所用到的样本集Xt中的数据会与其他时刻的样本集数据存在重复。可以看到样本集" 与样本集" 中的数据由于通过滑动窗口截取,数据" 到" 和" 到" 是相同的,为了让信息的传递符合实际情况,把每批次模型学完后第一个数据的信息" 作为下一批次模型学习的初始信息 。在模型学习中,把每批样本Xt的前Wtrain个数据作为训练集,计算每个数据输入模型后与真实值的损失函数 ,然后用总误差函数" 来优化模型。当总损失值小于规定阈值或达到学习次数时模型停止学习,对第Wtrain+1至Wtrain + Wtest数据进行预测。
2" 实证分析
2.1" 模型选取
选择被广泛应用于金融时间序列预测的CNN-LSTM [11]作为ROA的基础模型,其中CNN-LSTM的结构图如图4所示。
CNN-LSTM模型中构建了卷积层(conv1d)、LSTM层和一个全连接层(FC),数据依次通过一维卷积层、LSTM层和全连接层,最终得到输出。
CNN-LSTM参数设计如表1所示,输入的训练集数据为三维数据向量(1,60,5),其中,60表示时间步长的大小(即有60步的数据进行多步预测),5表示输入维度的5个特征(即黄金期货价格数据的开盘价、收盘价、最高价、最低价和交易量)。
首先,数据进入一维卷积层,进一步提取特征,得到一个三维输出向量(1,60,20)(其中20表示卷积核的大小)。然后,输出向量进入LSTM层进行训练,得到输出数据(1,60,20)(其中20表示LSTM节点大小)。将数据进行扁平化操作得到数据(1,1 200),进入一层全连接层,得到最终输出(1,1)。为了减少计算时间,快速得到结果,将模型首次学习最高学习次数设置为3 000,学习次数达到3 000时,模型停止学习进行测试,之后批次学习的学习次数最高为1 000。
2.2" 实验数据及模型评价指标
本次实验使用芝加哥商品交易所2011年11月28日至2023年11月20日黄金期货价格共2 000条数据,选取开盘价、收盘价、最高价、最低价和交易量共5个指标作为多特征输入,对黄金期货每天的收盘价进行预测。为了更好地训练模型,采用多数研究较常使用的归一化对数据进行[11]处理:
其中, 表示样本均值,σ表示样本标准差。在得到预测结果后,对预测结果进行反标准化处理,得到预测值。
作为神经网络预测模型,选取如下评价指标。
平均绝对误差指标(Mean Absolute Error, MAE)为:
均方根误差指标(Root Mean Square Error, RMSE)为:
R2拟合优度指标为:
其中,m表示数据集的长度,yi表示i时刻的真实值, 表示i时刻的预测值。
2.3" 实验结果及分析
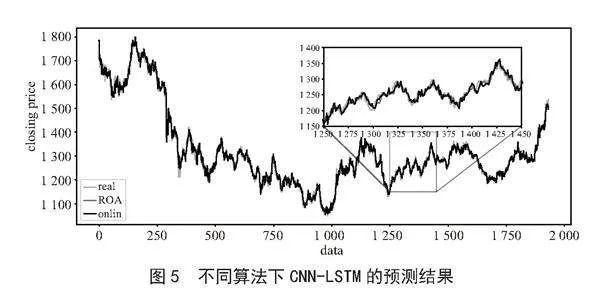
在ROA算法和传统在线学习算法下使用CNN-LSTM模型对黄金期货价格进行预测,分别画出股票价格的真实值(real,红色)、ROA算法下CNN-LSTM模型的预测值(ROA,蓝色)和传统在线学习算法下CNN-LSTM模型的预测值(online,黑色)的折线图,结果如图5所示。
从图5中可以看出,CNN-LSTM模型在ROA和传统在线学习算法下都有较好的预测效果,其中ROA算法下模型的预测值更为贴合真实值。
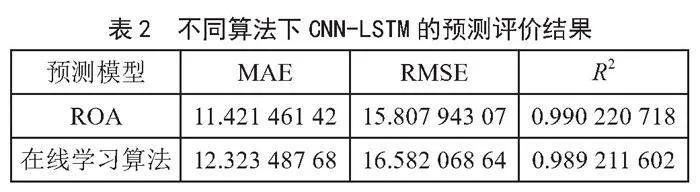
为了对ROA和传统在线学习算法的预测能力进行更为充分的评价,下面分别计算MAE、RMSE和R2指标值,得到的预测评价结果如表2所示。
从表2中可以看出,在所有评价指标中,ROA效果均优于传统在线算法,实验结果表明向传统在线学习算法中加入信息传递的确能提升模型的预测性能。
3" 结" 论
为了提高传统在线学习算法下模型对黄金期货的预测效果,采用CNN-LSTM模型向传统在线学习算法中加入信息传递,得到ROA。结果表明,向在线学习算法中加入信息传递的确能提升模型的预测性能。这对未来使用在线学习算法进行时间序列预测有一定的参考意义。
参考文献:
[1] 费一凡,陶雨芊.基于ARMA模型的黄金价格短期预测分析 [J].时代金融,2018(30):236-237.
[2] ASKARI M,ASKARI H. Time Series Grey System Prediction-based Models: Gold Price Forecasting [J].Trends in Applied Sciences Research,2011,6(11):1287-1292.
[3] BASHER S A,SADORSKY P. Hedging Emerging Market Stock Prices with Oil, Gold, VIX, and Bonds: A Comparison between DCC, ADCC and GO-GARCH [J].Energy Economics,2016,54:235-247.
[4] CHANG P C,FAN C Y,LIN J L. Trend Discovery in Financial Time Series Data Using a Case Based Fuzzy Decision Tree [J].Expert Systems with Applications,2011,38(5):6070-6080.
[5] SRINIVASAN N,LAKSHMI C. Stock Price Prediction Using Fuzzy Time-series Population Based Gravity Search Algorithm [J].International Journal of Software Innovation (IJSI),2019,7(2):50-64.
[6] GUO Y H,HAN S M,SHEN C H,et al. An Adaptive SVR for High-frequency Stock Price Forecasting [J].IEEE Access,2018,6:11397-11404.
[7] UROLAGIN S. Text Mining of Tweet for Sentiment Classification and Association with Stock Prices [C]//2017 International Conference on Computer and Applications (ICCA). Doha:IEEE,2017:384-388.
[8] WANG J Y,LI Y F,WANG T T,et al. A Gold Futures Price Forecast Model Based on SGRU-AM [J].IEEE Access,2021,9:146745-146754.
[9] SINGH T,KALRA R,MISHRA S,et al. An Efficient Real-time Stock Prediction Exploiting Incremental Learning and Deep Learning [J].Evolving Systems,2022,14:919-937.
[10] 刘成昊.在线学习算法研究与应用 [D].杭州:浙江大学,2017.
[11] LU W J,LI J Z,LI Y F,et al. A CNN-LSTM-based Model to Forecast Stock Prices [J].Complexity,2020(1):1-10.
[12] ELMAN J. Finding Structure in Time [J].Cognitive Science,1990,14(2):179-211.
作者简介:石岩松(1999—),男,汉族,云南保山人,硕士研究生在读,研究方向:机器学习;通讯作者:杨博(1987—),男,白族,云南昆明人,副教授,博士,研究方向:应用数学。
收稿日期:2023-12-04