



摘" 要:在不平衡数据集中,过采样的主要目的是通过增加少数类样本的数量来平衡数据集,而现有的过采样方法,只考虑了少数类样本之间的分布规律,并在少数类样本之间进行样本合成,这样会导致少数类样本的范围比实际范围小。针对上述问题,对凸显少数类样本范围的过采样方法进行研究。基于3种分类器(SVM、KNN、随机森林)与5种过采样算法(SMOTE、Borderline、KmeansSMOTE、SVMSMOTE、ADASYN)在4种不平衡数据集上开展实验,实验结果表明,应用凸显少数类样本范围的过采样算法在最优和第二优分类结果中占最高比例,因此在数据处理中应用该算法具有较好的效果。
关键词:数据处理;过采样方法;分类器
中图分类号:TP181;TP311.1 文献标识码:A 文章编号:2096-4706(2024)19-0027-07
Research on Oversampling Methods that Highlight the Range of a Few Class Samples
HUANG Xiuling, WEN Shangxi, CHEN Yiheng
(Shanghai Institute of Technology, Shanghai" 201418, China)
Abstract: In unbalanced datasets, the main purpose of oversampling is to balance the dataset by increasing the number of samples of a few classes. However, the existing oversampling method only considers the distribution law among the samples of a few classes, and conducts sample synthesis among the samples of a few classes, which will lead to a small range of samples of a few classes compared with its actual range. To solve the above problems, this paper researches the oversampling methods that highlight the range of a few class samples. The experiments are conducted on four kinds of unbalanced datasets based on three classifiers (SVM, KNN, Random Forest) and five oversamping algorithms (SMOTE, Borderline, KmeansSMOTE, SVMSMOTE, ADASYN). The experimental results show that the oversampling algorithm that highlights the range of a few class samples has the highest proportion of the optimal and second best classification results. Therefore, applying this algorithm in data processing has good results.
Keywords: data processing; oversampling method; classifier
0" 引" 言
随着数据挖掘技术、深度学习算法等技术的不断发展和应用,学者们对大数据的需求逐渐提高,然而数据不平衡问题却总是存在,且影响应用效果,如在情感诊断[1]、机械故障诊断[2]以及医疗诊断[3]等领域。由于机械故障诊断中非故障数据远远比故障数据多的情况,使分类器[4]无法有效地对该数据进行学习和分析。面对这种情况,可选择的解决方案有两种:一是通过增加机械故障次数来增加少数类样本个数,二是直接对样本数据进行处理。若采用第一种方案将导致时间与财产成本的巨幅增加,尤其对大型、贵重的机械很不友好,不可取。因此,第二种方案可行性更高,但需对已获取的样本进行处理。
重采样方法[5]是相对较优的一种样本处理的方法,分为欠采样方法[6]和过采样方法[7]。其中欠采样方法是将多数类样本的个数减少,使数据中各类样本的数量达到平衡,从而提升分类器的预测精度。其中,随机欠采样(RUS)[8]是最简单且直接的一种欠采样方法,即从多数类样本中随机抽取数据并删除,从而使多数类样本与少数类样本的数据量达到平衡。但如此可能会因样本总数减少,而导致分类器难以从数据中提取到有效信息,或可能在随机删除数据过程中直接将具有重要特征的数据删除,导致分类器无法准确地进行分析。
为解决随机欠采样方法带来的问题,过采样方法被提了出来。与欠采样方法相反,过采样方法是通过将少数类样本量增多的方式来达到正反样本量平衡的目的。其中,随机过采样(ROS)[9]是最简单且直接的一种过采样方法,即从少数类样本中随机抽取样本并复制,从而使少数类样本量增多,并与多数类样本数据量平衡。这种方法虽然增加了样本数量,使分类器可以提取更多的信息,同时提升了分类精度,但由于只是简单地对少数类样本进行复制,分类器的泛化性较弱,容易产生过拟合问题。
为解决随机过采样方法中容易产生过拟合的问题,SMOTE[10]方法被提了出来。SMOTE方法是在随机选取的少数类样本与其最近的少数类样本之间随机取点,并生成新数据。该方法取得了极好的效果,因此许多研究者基于SMOTE方法对过采样方法展开深入研究。
Borderline SMOTE[11]过采样方法是将少数样本分为三种级别:安全、危险和噪声,然后忽略噪声级别的样本,只对危险级别的少数类样本进行过采样;Radius SMOTE[12]过采样方法是将SMOTE方法中在两点连线中随机取一点的方式改为以选取的少数类样本为中心画圆,在圆中随机取点,基于K近邻算法计算得到半径;KmeansSMOTE[13]过采样方法是使用K均值聚类算法对整个数据进行聚类,从中选择少数类样本中数量多的集群,将新合成样本分配给少数类样本中数量较少的群集;SVMSMOTE[14]过采样方法结合了SVM算法,先使用SVM算法对原始数据进行分类,找出支持向量和非支持向量,然后基于少数类的支持向量生成新的样本;ADASYN[15]过采样方法是对每个少数类样本进行K近邻统计,将K近邻中多数类样本的比例作为一个权重因子,根据权重因子,计算每个少数类样本所需的合成样本的数量,最后,依次从少数类样本中随机选择一个少数类近邻并在二者间随机生成少数类样本。
以上的过采样方法均是考虑少数类样本之间的规律,并在两个少数类样本之间生成样本,这样生成的样本虽是有效,但无法明确凸显少数类样本范围或减少了其应有的范围。在实际中,多数类的判别错误比少数类的判别错误所付出的代价更大。本文提出一种更符合少数类样本分布规律,同时能更凸显少数类样本范围的过采样算法,提高分类器对不平衡数据的分类精度。本文通过3种分类器(SVM、KNN、随机森林)与5种过采样算法(SMOTE、Borderline、KmeansSMOTE、SVMSMOTE、ADASYN)在4种不平衡数据集上进行对比实验,从G-mean、F-measure、AUC指标的比较来看,该方法总体上优于其他方法。
1" 凸显少数类样本范围的过采样算法
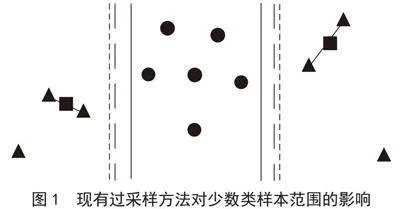
假设初始少数类样本(三角)的应有范围为细实线,通过分类器后的范围为细虚线,当采用现有过采样方法进行数据扩张(正方形)后,样本范围为粗虚线,可以看出这些方法对于少数类样本范围虽有凸显但并不是很明确,或者对少数类样本范围恢复不够,如图1所示。
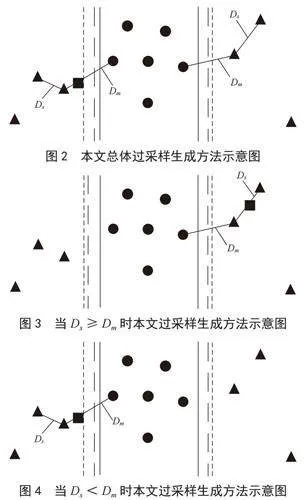
为解决上述问题,本文提出一种凸显少数类样本范围的过采样算法,如图2所示。具体原理为:
1)随机选择少数类样本A。
2)计算与A最近的少数类样本距离Ds和最近的多数类样本距离Dm。
3)比较Ds与Dm的大小,如果Ds≥Dm,则在选取点A与最近少数类样本之间合成新样本,如图3所示;如果Ds<Dm,则在选取点A与最近多数类样本之间合成新样本,如图4所示。
2" 算法过程
对于本文所提算法,在少数类样本和多数类样本之间合成点的方式相对比其他过采样方法来说是更危险的,在多数类样本区域合成少数类样本的概率更大。因此,本文设置一个权重因子w来控制合成样本的位置更靠近少数类样本区域,使合成的位置更为安全,同时确保少数类样本区域的不确定性,在w中加入安全因子r(0到1的随机浮点数)模拟样本生成的不确定性。
具体算法过程如下几点:
1)将不平衡数据集划分为少数类样本和多数类样本。
2)随机从少数类样本中挑选样本作为选择点P,找出离选择点最近的少数类样本Ps和多数类样本Pm并计算其与选择点P的欧式距离,分别为Ds、Dm。
3)比较Ds与Dm的大小,当Ds<Dm时,生成的少数类样本Pnew的计算式为:
(1)
(2)
4)当Ds≥Dm时,生成的少数类样本Pnew的计算式为:
(3)
(4)
3" 实验结果与分析
本文在Window 11(64位)操作系统,Intel Core i7-12700H CPU @2.3 GHz,16 GB RAM的环境下使用Python进行实验。
3.1" 数据集
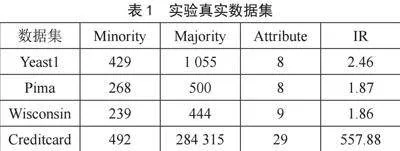
为了测试本文算法的有效性,本文使用KEEL[16]和UCI[17]中4个公开数据集(Yeast1、Pima、Wisconsin与Creditcard)进行测试,如表1所示。其中Minority、Majority、Attribute和IR分别代表少数类样本数量、多数类样本数量、特征数量和不平衡比例。不平衡的比例等于多数类样本数量除以少数类样本数量,如表1所示。
3.2" 不平衡分类的评价指标
本文将选取不平衡数据分类的常用评价指标G-mean、F-measure和AUC来反映模型性能的优劣[18]。其中,TP表示模型正确分类的正类样本数量,FN表示模型错误分类的正类样本数量,FP表示模型错误分类的负类样本数量,TN表示模型正确分类的负类样本数量,如表2所示。
几何均值G-mean综合考虑了分类模型对正类和负类样本的性能,涵盖了灵敏度(真正例率)和特异性(真负例率),能够全面评估模型的整体分类性能,公式为:
(5)
正类检验值F-measure结合了精确度和召回率,能够评估模型在少数类(在不平衡数据中通常是正类)上的性能,公式为:
(6)
ROC[19]曲线上的点对应模型在不同概率阈值下的表现,其中横坐标表示负类别样本被错误分类为正类别的概率(False Positive Rate, FPR),纵坐标则表示正类别样本被正确分类为正类别的概率(True Positive Rate, TPR)。ROC曲线下的面积,即AUC(Area Under the Curve)[19],是一个衡量模型性能的指标。当AUC等于0.5时,模型性能等同于随机分类,而数值越接近1则表示模型性能越好。公式为:
(7)
(8)
3.3" 合成数据对比
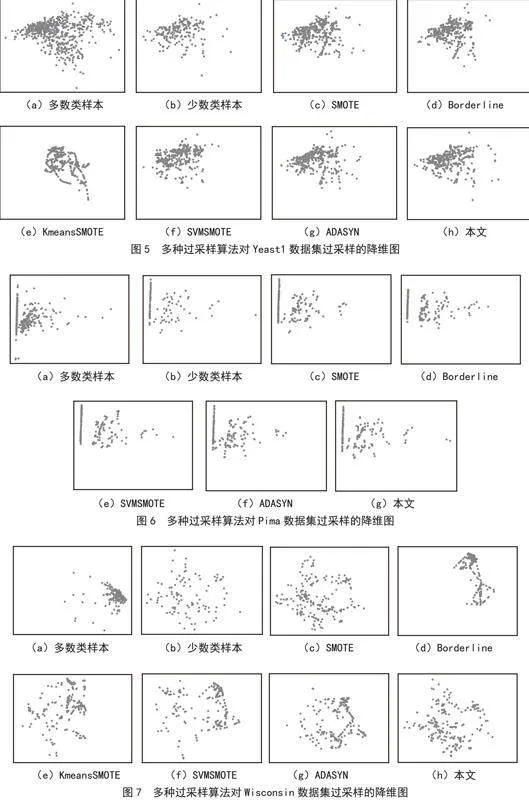
对于4种不同的数据,使用多种过采样算法(SMOTE、BorderlineSMOTE、K-meansSMOTE、SVMSMOTE、ADASYN以及本文算法)分别对少数类样本进行过采样,对于所有的样本,其特征是多维的,本文使用PCA技术[20]来将特征降维到二维方便观察。如图5至图8所示,其中子图(a)(b)分别为多数类样本和少数类样本的降维图,子图(c)~(h)为不同过采样算法合成样本的降维图(Pima数据集中KmeansSMOTE算法无法合成足够的少数类样本,因此将其排除)。
从图5至图8的降维图中可以看出,本文算法与其他算法相比,合成的少数类样本的分布规律,即合成的少数类样本与原始的少数类样本降维图的分散程度更为相似,同时合成范围更为分散,使得少数类样本在安全的情况下范围更为凸显。
3.4" 实验结果分析
本研究将数据集中少数类样本平均分为两份:分别命名为Trs(用于训练)和Tes(用于测试);选取多数类样本(多数类样本数量是少数类样本的3倍)Trd(用于训练),同时选取多数类样本(多数类样本数量与少数类样本相同)Ted(用于测试)。将Trs和Trd数据集合并作为训练数据集(Tr),Tes和Ted数据集合并作为测试数据集(Te)。
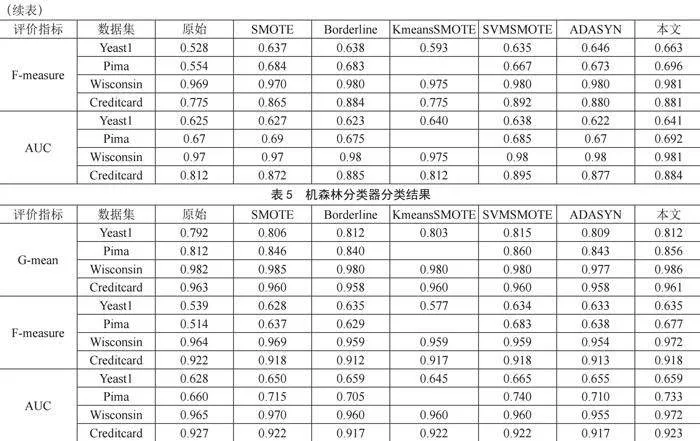
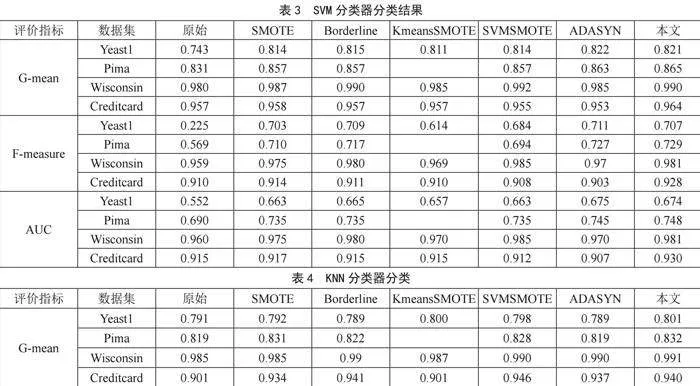
为了更好地说明本文算法对于多数分类器的适用性,本文选择SVM[21]、KNN[22]以及随机森林[23]分类器进行实验。分别对Tr和Te数据集基于6种过采样方法处理后,再应用于3个分类器,计算每个分类器下、经过不同过采样方法(6种方法)后得到的评价指标:G-mean,F-measure和AUC。实验结果如表3至表5所示。其中无数据表示无法生成足够的少数类样本(Pima数据集中KmeansSMOTE算法无法合成足够的少数类样本,因此将其排除),需排除。由于过采样算法选取样本具有随机性,本研究中所有实验分别进行100次,再取平均值。
从表3至表5可知,本文提出的过采样算法在这些数据集中均表现出良好的效果,无论是G-mean,F-measure还是AUC指标,其对应的值均为最优或第二优。而且当其评价指标处于第二优时,其值与第一优间相差约0.001~0.005,而与其他过采样算法间相差较大,如表5所示,基于随机森林分类器对Wisconsin数据集进行分类时,三个评价指标均为最优;此外,表4中,无论哪个数据集,应用本研究提出的过采样算法后,再基于KNN分类器的分类效果表现最优。
4" 结" 论
本文针对多数过采样算法在合成数据时只考虑少数类样本从而导致少数类样本的范围相比于其实际的范围小的问题,提出了一种凸显少数类样本范围的过采样方法,通过比较选取点最近的少数类样本及最近的多数类样本的距离来确定生成点的方向,然后通过比较的距离来确定生成点的位置。本文通过3种分类器与5种过采样算法在4种不平衡数据集上进行对比实验,实验结果表明经过本文提出的过采样算法对数据进行预处理后,可以提升各类分类器的分类效果,对不平衡数据集的合理扩充有一定效果。
参考文献:
[1] MOUNTASSIR A,BENBRAHIM H,BERRADA I. An Empirical Study to Address the Problem of Unbalanced Data Sets in Sentiment Classification [C]//2012 IEEE International Conference on Systems, Man, and Cybernetics (SMC).Seoul:IEEE,2012:3298-3303.
[2] DUAN L X,XIE M Y,BAI T B,et al. A New Support Vector Data Description Method for Machinery Fault Diagnosis with Unbalanced Datasets [J].Expert Systems with Applications,2016,64:239-246.
[3] RAHMAN M M,DAVIS D. Addressing the Class Imbalance Problem in Medical Datasets [J].International Journal of Machine Learning and Computing,2013:224-228.
[4] TULYAKOV S,JAEGER S,GOVINDARAJU V,et al. Review of Classifier Combination Methods [J].Machine Learning in Document Analysis and Recognition,2008,90:361-386.
[5] FABER N M. Comment on a Recently Proposed Resampling Method [J].Journal of Chemometrics,2001,15(3):169-188.
[6] YU H L,NI J,ZHAO J. ACOSampling: An Ant Colony Optimization-Based Undersampling Method for Classifying Imbalanced DNA Microarray Data [J].Neurocomputing,2013,101:309-318.
[7] ZHENG Z Y,CAI Y P,LI Y. Oversampling Method for Imbalanced Classification [J].Computing and Informatics,2015,34:1017-1037.
[8] TAHIR M A,KITTLER J,YAN F,et al. Concept Learning for Image and Video Retrieval: The Inverse Random Under Sampling Approach [C]//2009 17th European Signal Processing Conference.Glasgow:IEEE,2009:574-578.
[9] PANG Y,CHEN Z X,PENG L Z,et al. A Signature-Based Assistant Random Oversampling Method for Malware Detection [C]//2019 18th IEEE International Conference On Trust, Security And Privacy In Computing And Communications/13th IEEE International Conference On Big Data Science And Engineering (TrustCom/BigDataSE).Rotorua:IEEE,2019:256-263.
[10] CHAWLA N V,BOWYER K W,HALL L O,et al. SMOTE: Synthetic Minority Over-Sampling Technique [J].Journal of Artificial Intelligence Research,2002,16(1):321-357.
[11] HAN H,WANG W Y,MAO B H. Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning [C]//International Conference on Intelligent Computing, ICIC 2005.Hefei:Springer,2005.
[12] PRADIPTA G A,WARDOYO R,MUSDHOLIFAH A,et al. Radius-SMOTE: A New Oversampling Technique of Minority Samples Based on Radius Distance for Learning From Imbalanced Data [J].IEEE Access,2021,9:74763-74777.
[13] DOUZAS G,BACAO F,LAST F. Improving Imbalanced Learning Through a Heuristic Oversampling Method Based on K-means and SMOTE [J].Information Sciences,2018,465:1-20.
[14] WANG Q,LUO Z H,HUANG J C,et al. A Novel Ensemble Method for Imbalanced Data Learning: Bagging of Extrapolation-SMOTE SVM [J/OL].Computational Intelligence and Neuroscience,2017,2017(1):1827016[2024-02-16].https://doi.org/10.1155/2017/1827016.
[15] HE H B,BAI Y,GARCIAET E A,et al. ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning [C]//2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence).Hong Kong:IEEE,2008:1322-1328.
[16] ALCALÁ-FDEZ J,SANCHEZ L,GARCIA S,et al. KEEL: A Software Tool to Assess Evolutionary Algorithms for Data Mining Problems [J].Soft Computing,2009,13:307-318.
[17] UC Irvine Machine Learning Repository [EB/OL].[2024-02-16].http://archive.ics.uci.edu/.
[18] POWERS D M W. Evaluation: From Precision, Recall and F-measure to ROC, Informedness, Markedness and Correlation [J/OL].arXiv:2010.16061 [cs.LG].[2024-02-17].https://doi.org/10.48550/arXiv.2010.16061.
[19] CHAWLA N V,BOWYER K W,HALL L O,et al. SMOTE: Synthetic Minority Over-Sampling Technique [J].Journal of Artificial Intelligence Research,2002,16(1):321-357.
[20] PIROGOV L E,ZEMLYANUKHA P M. Principal Component Analysis for Estimating Parameters of the L1287 Dense Core by Fitting Model Spectral Maps into Observed Ones [J].Astronomy Reports,2021,65:82-94.
[21] JOACHIMS T. Making Large-Scale SVM Learning Practical [R/OL].Technical Reports,1998[2024-02-10].https://www.econstor.eu/bitstream/10419/77178/2/1998-28.pdf.
[22] GUO G,WANG H,BELL D,et al. KNN Model-Based Approach in Classification [C]//OTM Confederated International Conferences CoopIS, DOA, and ODBASE 2003.Catania:Springer,2003:986-996.
[23] PAL M. Random Forest Classifier for Remote Sensing Classification [J].International Journal of Remote Sensing,2005,26(1):217-222.
作者简介:黄秀玲(1981—),女,汉族,浙江平阳人,讲师,博士,研究方向:深度学习算法、列控系统仿真;温尚锡(1996—),男,汉族,山西朔州人,硕士在读,研究方向:深度学习算法;陈一衡(1997—),男,汉族,山东日照人,硕士在读,研究方向:数据处理和列车运行控制。
基金项目:上海市科委项目(21210750300);校级项目(10120K6060-A06)