
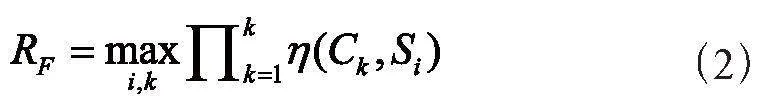
摘" 要:为分析房价影响因素,选择更优的机器学习模型预测房价走势,使用两种机器学习算法构建了两种预测模型并对比预测效果。通过对公开数据集进行特征分析、预处理以及数据集划分,构建了多元线性回归预测模型和随机森林预测模型。采用平均绝对误差(MAE)、均方根误差(RMSE)以及决定系数(R2)作为最终评估模型的指标,结果显示随机森林模型的平均绝对误差、均方根误差较小,决定系数较大。评估得出随机森林模型预测准确性较多元线性回归模型更优。
关键词:多元线性回归;随机森林;房价预测
中图分类号:TP391;F224 文献标识码: A 文章编号:2096-4706(2024)22-0127-05
Comparative Research on House Price Forecast Model Based on Multiple Linear Regression and Random Forest Algorithm
Abstract: To analyze the influencing factors of house price and select a better Machine Learning model for forecasting house price trend, two forecasting models are constructed using two Machine Learning algorithms and the forecasting results are compared. The Multiple Linear Regression forecasting model and Random Forest forecasting model are constructed by analyzing features of public datasets, preprocessing, and partitioning datasets. Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and R-squared (R2) are used as indicators for evaluating the final model. The results indicate that the Random Forest model has lower MAE and RMSE values and a higher R-squared. The evaluation shows that prediction accuracy of the Random Forest model is better than that of the Multiple Linear Regression model.
Keywords: Multiple Linear Regression; Random Forest; house price forecast
0 引" 言
自2003年国务院18号文件正式确立房地产业是国民经济支柱产业的地位之后,我国房地产业快速发展,并带动房价在过去的二十多年经历较大幅度的持续上涨[1]。2016年12月中旬,中央经济工作会议提出,要坚持“房子是用来住的,不是用来炒的”的定位,要求回归住房居住属性[2]。2020—2022年三年的疫情防控下,房地产市场跌宕起伏。房价的高低成为关系到居民切身利益的重大经济问题和社会问题。在此背景下,房价的影响因素和房价预测成为学者研究的热点领域。
学者们通过采用数学模型来分析房价数据,预测房价走势,分析房价的影响因素并进行广泛研究。李贤增基于线性模型和非线性模型进行房价预测[3],罗博炜等人对房价数据采用多元线性回归算法设置虚拟变量建模[4]。李然等人基于神经网络算法对房价进行预测,并结合均方误差的值给出合理的预测区间,为解决房价预测问题提供了新思路[5]。Singh等人使用三种机器学习算法进行比较,即线性回归、随机森林回归和使用Python决策树回归,结果显示使用机器学习算法预测房价是预测房价的最快方法[6]。Zou选择具有大量特征的数据集,采用最小二乘法和随机森林算法进行建模,并对两种预测模型进行评估,结果表明两种算法都能够精准的进行房价预测[7]。基于目前的研究现状,很多研究方法都是使用机器学习算法来预测房价,如:时间序列分析算法,逻辑回归算法,线性回归算法,神经网络算法,随机森林算法等。
本文应用与房价走势高度相关的影响因素经济指标, 借助公开的数据集,使用多元线性回归算法和随机森林算法构建模型, 并且对比分析两个模型的预测准确度,从而选择更优的房价预测模型。
1" 模型介绍
1.1" 多元线性回归算法模型
多元线性回归的主要原理是构建一个包含多个自变量和一个因变量的回归方程,根据多个自变量的值来解释和推断因变量的值。由于事件间的关系往往是多方面的,造成事情发生的各种因素有许多。因此,使用多种自变量组成的最优集合来预测因变量比使用单独的自变量进行预测,得到的预测结果更加精确,也更加符合实际。多元线性回归模型的核心是构建一个函数,能够达到预测值与真实值之间的差值的平方值最小。多元线性回归模型通常用来描述变量Y和X之间的随机线性关系,设定Y代表因变量,X1、X2,…,Xn代表的是自变量,多元线性回归方程表示为:
Y=β0+β1X1+β2X2+…+βnXn+e" " " " " " " " " (1)
方程式中的β0、β1,…,βn为回归系数,e为随机变量。
使用多元线性回归还需要达到以下的三个条件:
1)Y和X之间必须具备随机线性关系。
2)各观测值Y相互独立。
3)残差e服从均值为0,方差为δ2的正态分布,也就是对自变量的任意一组观测值,因变量Y具有相同的方差,且服从正态分布。
1.2" 随机森林算法模型
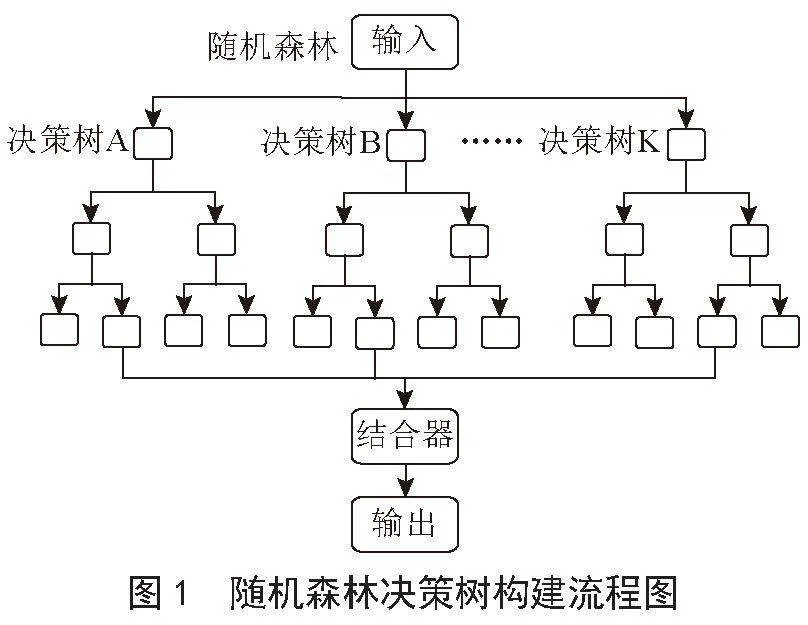
随机森林算法是集成学习(Ensemble Learning)对决策树的实现,利用投票机制进行决策分类及回归预测。方法是一次训练多个决策树,综合考虑多个结果,最终得到预测结果。每颗决策树的分割节点数目均是根据样本特征数随机确定的,随机森林算法决策树的构建流程如图1所示。
首先对原始样本集进行抽样以获得K个样本,并将其建模成决策树,即弱分类器;接着每个弱分类器均会产生相应的决策结果,再选择相应的变量建模成决策树,以此获得具有K棵决策树的随机森林;最后利用投票机制寻得最高分的树,且将其作为最终结果输出[8]。
随机森林算法模型RF为:
式中,Si为第i个样本集;Ck为第k棵决策树;
2" 数据获取与数据预处理
2.1" 数据获取
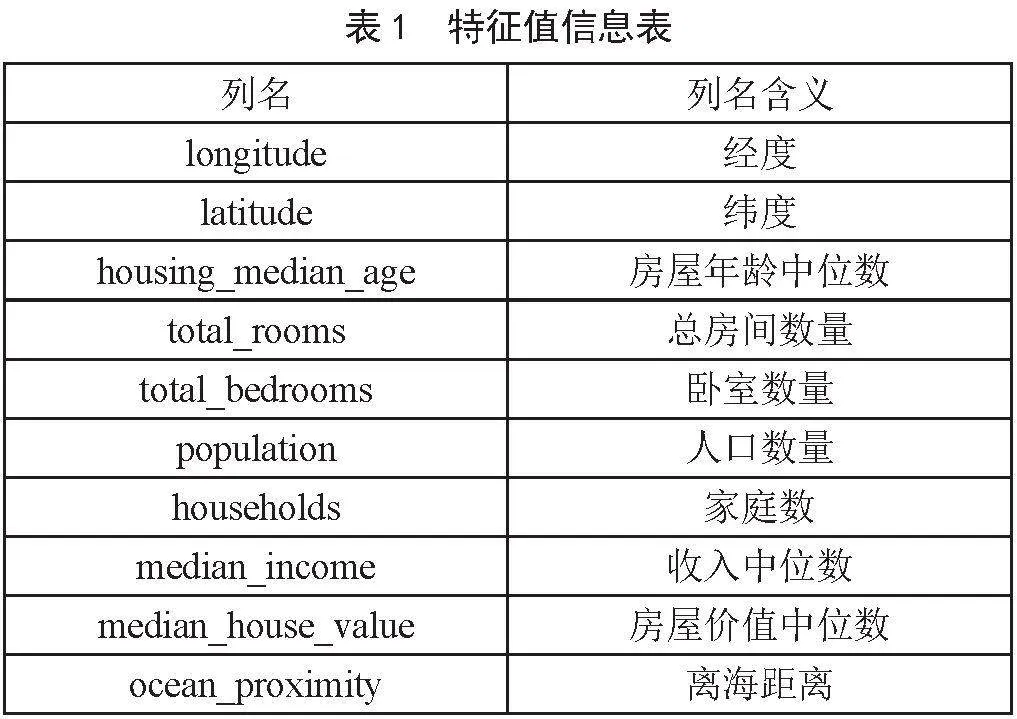
本文采用网络公开数据集进行模型构建与对比实验,具体数据集为加州2021年度房价数据集,共20 000余条数据。数据集中每行数据表示一个街区,包括共有10个属性:总的房间数量、卧室的数量、人口数量、收入等10个房屋特征,房屋每个特征都附有详细描述,这为本文的预测研究在选取合适的特征值时提供了很大便利,具体特征值的信息如表1所示。
2.2" 数据预处理
数据的质量对于模型的预测效果至关重要,在构建模型之前,需要对收集到的数据进行进一步处理。本文的数据处理以及模型构建使用Python语言,调用Python的numpy和pandas库对数据进行数据清洗和处理,调用Python的matplotlib库进行绘图,调用Python的机器学习库Scikit-Learn(sklearn)进行数据建模。
2.2.1" 特征相关性研究
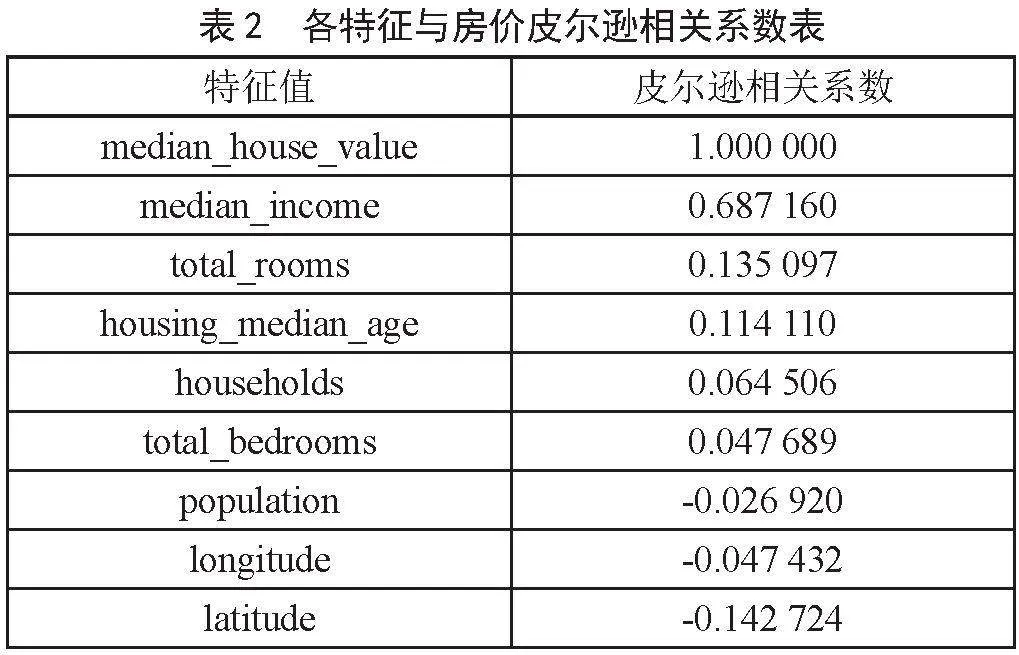
为找出各个属性同房价之间的相关性,可以直接使用corr函数计算出每两个属性的皮尔逊相关系数。相关系数的取值区间[-1,1],系数越靠近1则说明有越强的正相关,越靠近-1说明有越强的负相关。为了找出特征属性与房价之间的相关性,此处通过计算列出每个特征属性和房价的相关系数。
根据表2可以看出特征值median_income与特征值median_house_value的皮尔逊相关系数数值较大,其他特征值相关系数较小。
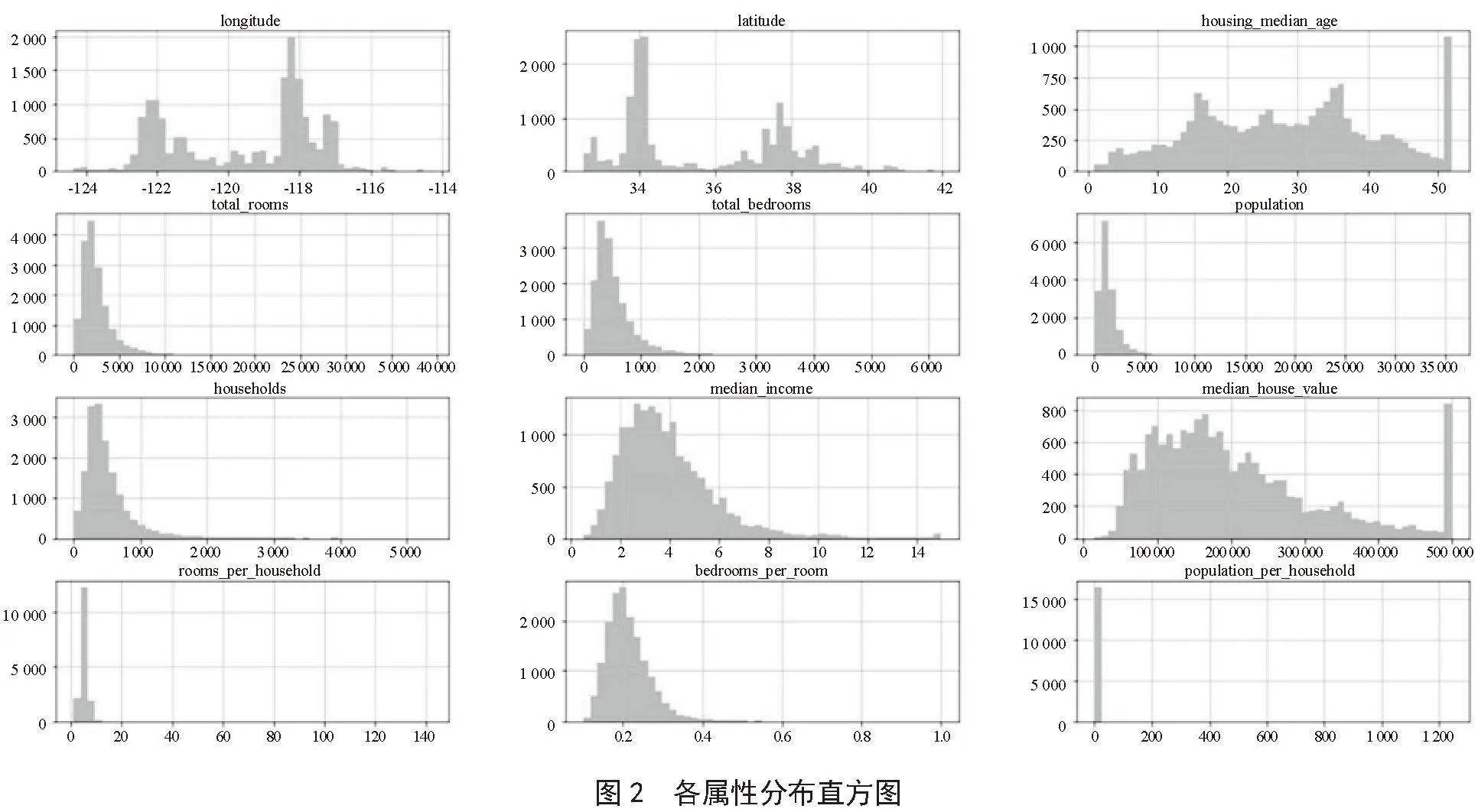
除了目前数据提供的特征属性以外,也可以通过创建新的属性组合来研究属性组合与房屋价格之间的相关性。通过简单的数学计算可以就得到:各家庭房间数量(rooms_per_household)、各家庭成员数量(population_per_household)、各房间中卧室的占比(bedrooms_per_room)。可以根据各个属性的数据绘制直方图,进一步了解各属性的分布情况。根据图2各属性分布直方图可以看出各个属性被缩放的程度各不相同。房屋年龄中位数和房屋价格中位数设置存在上限,可以明显看出房屋年龄中位数在50年之后和房屋价格中位数在50万之后的数据量突然激增。结合直方图的前段部分来看,说明这部分存在一些不符合规律的异常值,为了保证预测的准确性,在进行建模之前,需要对这些异常数据进行剔除。剔除某些数据后重新计算每个特征属性和房价相关系数。
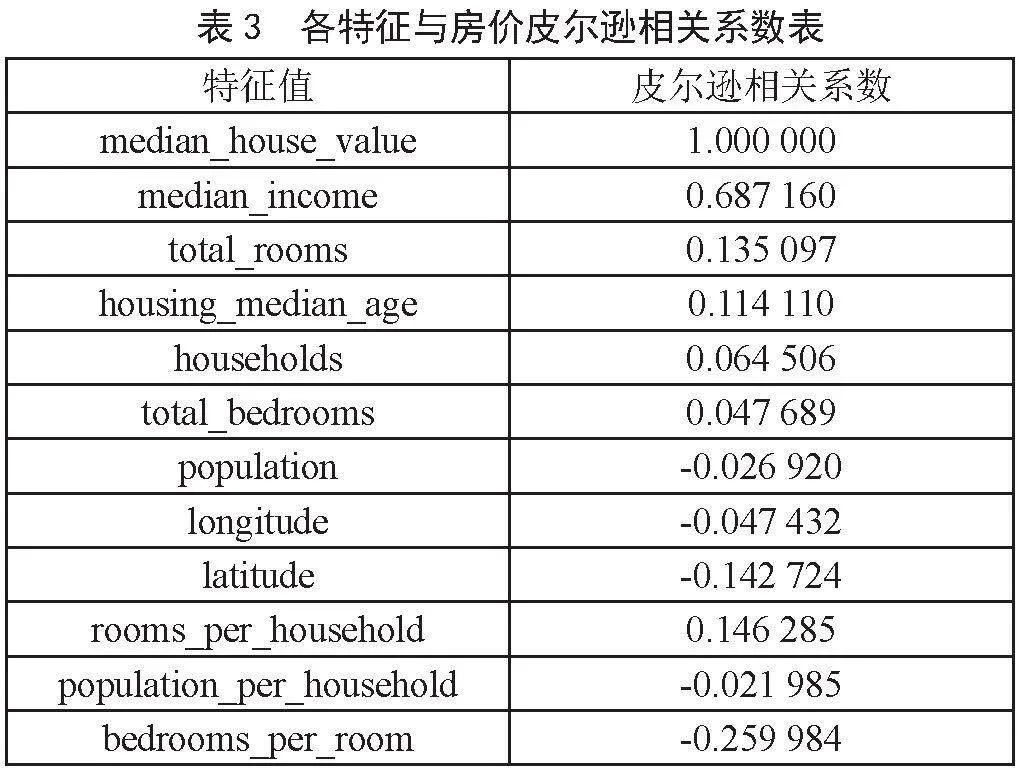
根据表3各特征与房价皮尔逊相关系数表可以看出,特征值rooms_per_household相比于特征值total_rooms与median_house_value的相关性更高,特征值population_per_household相比于特征值population与median_house_value的相关性要低一些。
2.2.2" 缺失值处理
在数据收集的过程中,会有很多情况导致收集到的数据存在缺失值,需要采用专业的处理方式处理缺失数据。
缺失值的处理方法分为三大类:删除、不做处理、填充。如果对缺失值不做处理,直接采用包含缺失值的数据建立预测模型,得到的预测值将与真实值产生不可预估的差距。如果直接删除缺失值,当缺失值数量较多时,采用这种方法会造成信息不完整不符合真实情况的问题,从而影响模型的预测结果。
本文选择采用最接近真实情况的中位数填充缺失值,中位数是一列数据中处于最中间值的位置,不容易受到该数据中极大值和极小值的影响,在一定程度上对该列数据具有代表性。
使用info()可以看到数据的属性,数据每列的非空值个数和类型,可以观察到total_bedrooms这列存在缺失值,通过sklearn库中的SimpleImputer类使用中位数填补缺失值。
2.2.3" 非数值型数据转换
选取的房价数据中ocean_proximity这一项的数据类型为类别型数据,该列的各个值分别代表一种类别,需要将其类别从文本型转换成数字型。
问题是模型被训练成认为两个接近的值比两个相距很远的值更相似。在当前序列类别中,相邻情况下1h ocean与near ocean之间的相似性高于1h ocean与inland之间的相似性。一个常见的解决方案是为每个类创建一个二进制属性:当类别为1h ocean时,它的一个属性为1(其他属性为0),当类别为inland时,另一属性为1(其他属性为0),这就是独热编码[9],可以使用sklearn的OneHotEncoder 编码器,将整数类别值转换成独热向量。
3" 模型构建与实验结果
3.1" 模型评价的标准
想要对比不同的模型的预测效果,需要先选择一套合适精准的评价指标来对预测模型进行准确评估。不同的类型的算法模型对应相同评价指标的表现也会不同。
一般来说,在分类问题中,主要使用精确率、召回率、正确率、错误率以及POC曲线等指标作为评价指标。回归问题的评价指标也有很多种,包括平均绝对误差、平均绝对百分比误差、均方根误差、决定系数R2、皮尔逊相关系数等。本文所研究的房价预测模型针对的是一个回归问题,主要采用决定系数(R2)和均方根误差(RMSE)对预测模型进行评估。
均方根误差(RMSE):用于衡量模型效果的指标,它是通过均方误差开根得到的,可以从单位度量的角度来评估模型的表现。误差值越小,得到的预测值与真实值之间的差值也就越小,说明建立的模型效果越好。
决定系数(R2):衡量模型拟合数据程度的统计指标。说明自变量能够通过回归模型所解释的因变量波动的占比。当决定系数接近1时,说明自变量对因变量的解释能力非常强,这意味着模型的预测能力就越强。
3.2" 数据集的划分
在构建模型之前,需要将原始数据集分为三部分:训练集、验证集和测试集。训练集的作用是建立一个模型,通过在这个模型上训练数据集可以获得一个泛化模型,然后运用到验证数据集,验证集的作用是检验模型的预测能力,根据验证集在模型上得到的预测结果对模型进行进一步的调参,测试集的作用是导入最终建立好的预测模型,得出预测结果,用来对预测模型进行准确度测试和拟合能力的检验。
为了测试集可以展现不同收入类型,本文选取分层抽样的形式划分数据集。收入的中位数是一个连续值属性,必须先对它进行区间的划分,转换成类别属性才能进行分层抽样。根据绘制的分布图,收入的中位数主要集中在区间[1.5,6],通过pd.cut()将收入分成5个类别:0~1.5、1.5~3、3~4.5、4.5~6、6~+∞。然后通过Sklearn的StratfiedShuffleSplit()进行数据划分。
3.2.1" 多元线性回归模型
调用Sklearn中线性模型的LinearRegression类构建线性回归模型对象,导入事先划分好的训练集进行模型训练,输入数据进行预测得到预测结果。
为了避免一些只在训练集上训练模型造成的弊端,可以使用交叉验证[10]的方式进行进一步的验证。本文采取的是k折交叉验证,其主要思想是对原始数据进行k次划分,每一次划分都进行一次模型训练和评估,在最后得到的k次评估结果中取平均值。调用Sklearn中的cross_val_score模块计算上述评估指标。
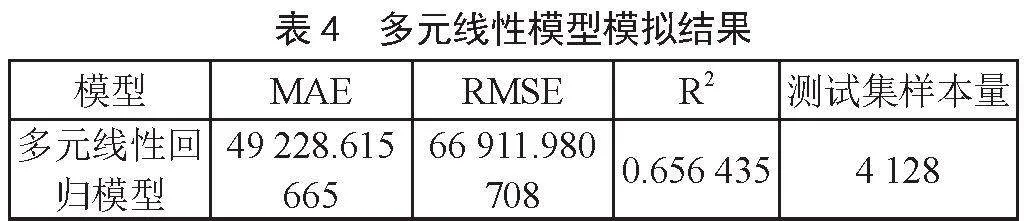
多元线性回归模型预测结果如表4所示。
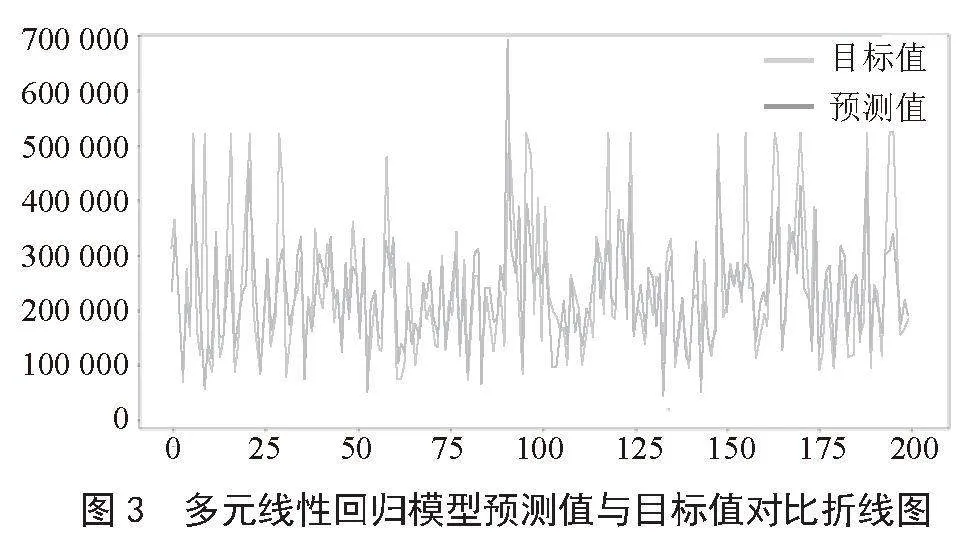
黑色线条代表预测值,灰色线条代表目标值。图3是根据4 128条数据的目标值与预测值绘制而成的折线图,将4 000多条数据一一对比展现是比较困难的,本图只截取了其中的200个数据进行图形绘制,根据这200个数据的可视化结果可以看出,多元线性回归模型的预测结果与真实结果在绝大部分数据上接近的,但依旧存在着部分差距。
3.2.2" 随机森林模型
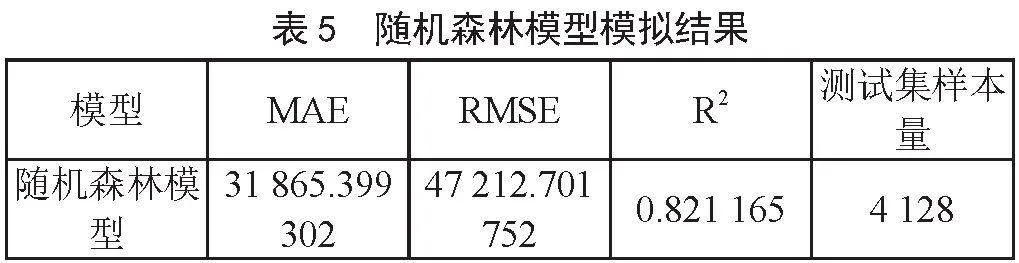
调用Sklearn中ensemble模块的RandomForestRegressor类构建随机森林模型对象。设置随机森林中决策树的数量,决策树的数量越大占用的相应内存越多。同时也将延长训练和预测的时间,因此在设置树的数量时也要综合考虑设备内存和性能。导入事先划分好的训练集进行模型训练,输入数据进行预测得到预测结果。调用Sklearn中的cross_val_score模块计算评估指标的值。随机森林模型预测结果如表5所示。
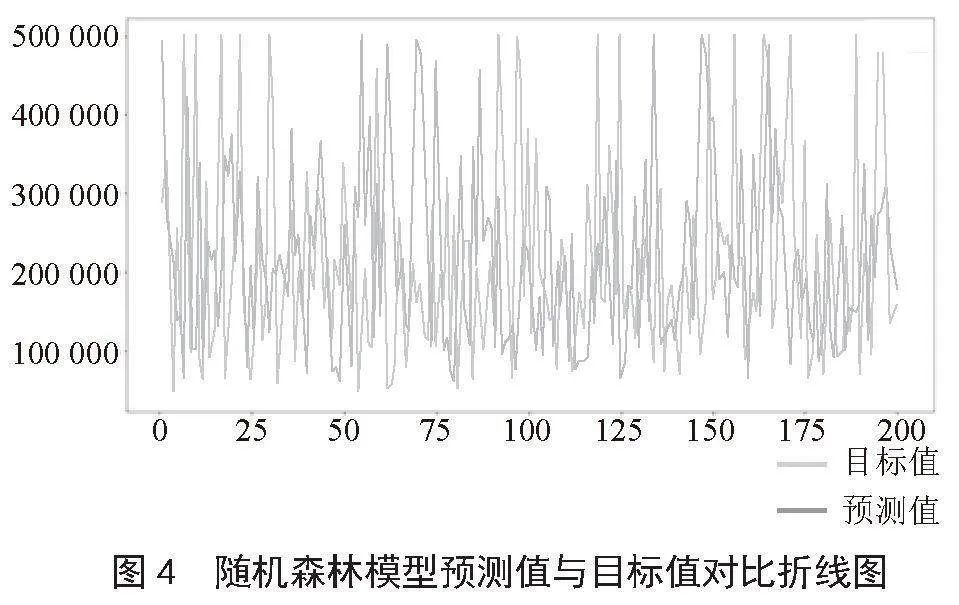
黑色线条代表预测值,灰色线条代表目标值。图4是根据4 128条数据的目标值与预测值绘制而成的折线图,将4 000多条数据一一对比展现较为困难,本图只截取了200个数据进行图形绘制,根据200个数据的可视化结果可以看出虽然随机森林预测结果趋势与目标值并没有完全相符,还是存在一些差距,但在大部分观测点上可以达到较为近似的预测效果。
4" 模型对比分析
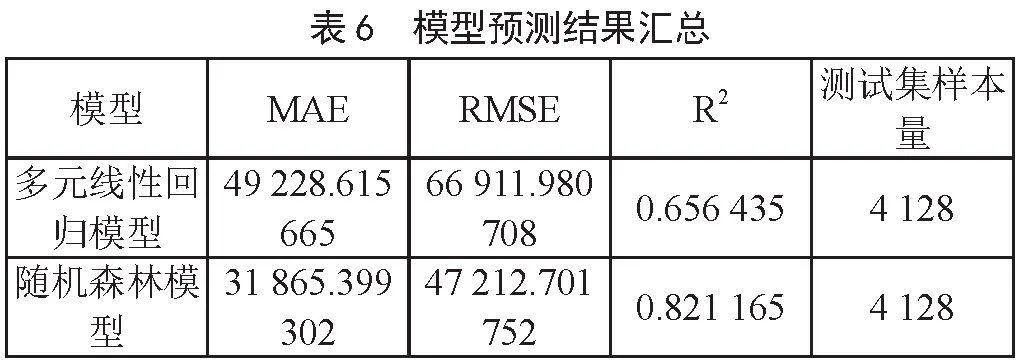
通过计算平均绝对误差、均方根误差和决定系数来评价和对比分析预测模型的预测效果。将两个模型的预测结果汇总如表6所示。
误差值越小,得到的预测值与真实值之间的差值也就越小,说明建立的模型越好。对比2个模型的平均绝对误差,多元线性回归模型的平均绝对误差为49 228.615 665,随机森林模型的平均绝对误差为31 865.399 302,从平均绝对误差的值来看,随机森林模型的效果较好。结合均方根误差的表现,多元线性回归模型的均方根误差为66 911.980 708,随机森林模型的均方根误差为47 212.701 752,多元线性回归模型预测误差要比随机森林模型大,说明模型的预测效果相比随机森林模型较差。决定系数(R2)的值越接近于1,则说明自变量对因变量的能够解释的程度就越高,模型效果也就越好。对比两个模型的决定系数的值,多元线性回归模型的决定系数为0.656 435,说明可以解释因变量65%的变异,随机森林模型的决定系数为0.821 165,说明可以解释因变量82%的变异,根据决定系数的值可以得出随机森林模型在该房价数据集上的预测效果较好。根据最终的预测结果计算的评价指标综合看出这两个模型之中,随机森林模型的表现较优。
5" 结" 论
对房价有影响的因素有很多,本文只着重考虑了比较核心的几项影响因素:房屋年龄、房屋结构、人均收入、地理位置等。还有经济发展水平、政府政策、人口结构等因素,选取更多相关的特征值对于房价预测的模型准确性会有更高的提升。在构建预测模型的过程中,可以尝试将不同模型采用stacking堆叠法进行模型融合,通过不同算法的融合对模型的准确率会有更高提升。
参考文献:
[1] 周亮锦,赵明扬.基于随机森林的深圳二手房价格分析 [J].中国市场,2022(26):68-71+133.
[2] 徐颖,黄素珍.大数据时代房地产价格预测模型的研究 [J].中国商论,2017(4):134-137.
[3] 李贤增.基于多元回归分析和支持向量机的房价预测 [D].北京:清华大学,2019.
[4] 罗博炜,洪智勇,王劲屹.多元线性回归统计模型在房价预测中的应用 [J].计算机时代,2020(6):51-54.
[5] 李然,章政,缪华昌.基于神经网络模型的房价预测研究 [J].中国集体经济,2022(27):94-96.
[6] SINGH A,CHAUDHARY C. House Prices Using Machine Learning Algorithms [C]//Proceedings of 5th ICMETE 2021.Singapore:Springer Nature Singapore,2022:747-758.
[7] ZOU H Y. Machine Learning-Based Analysis of Housing Price Predictors [J/OL].Academic Journal of Business amp; Management,2023,5(2)[2024-03-18].https://francis-press.com/papers/9179.
[8] 周云浩,杨宝杰,刘丹,等.基于随机森林算法的电力工程数据预测分析建模与仿真[J].电子设计工程,2024,32(4):103-106+111.
[9] 奥雷利安·杰龙.机器学习实战:基于Scikit-Learn和TensorFlow [M].北京:机械工业出版社,2018.
[10] 路佳佳.基于交叉验证的集成学习误差分析 [J].计算机系统应用,2023,32(1):302-309.