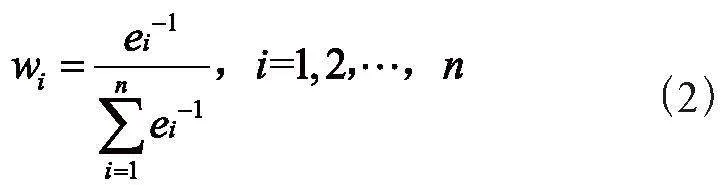
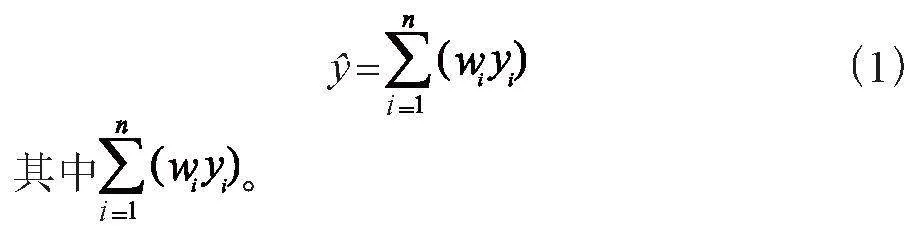
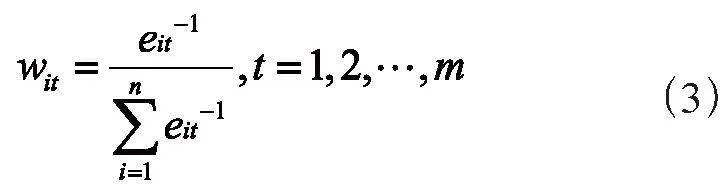
摘" 要:碳排放量的预测一直是国内外人们关注的热点,为了进一步提高碳排放量预测模型的准确性,考虑多种因素对碳排放量的影响,利用支持向量机回归、岭回归和BP神经网络三种传统单项碳排放量预测模型,结合误差倒数法构建了一种变权组合模型,并利用新模型预测我国2022—2026年的碳排放量。实证结果显示,组合模型的拟合精度和预测精度分别为99.26%和99.34%,组合模型对比3种单项模型有更高的精度。组合模型的预测结果显示,到2026年,我国碳排放增速较现在有所放缓,以1.8%的速度保持增长。
关键词:支持向量机回归;岭回归;BP神经网络;变权组合模型
中图分类号:TP18" " 文献标识码:A" 文章编号:2096-4706(2024)22-0122-05
Carbon Emission Prediction Based on Variable Weight Combination Model
Abstract: The prediction of carbon emissions has always been a hot spot of peoples attention at home and abroad. In order to further improve the accuracy of the carbon emission prediction model, considering the impact of multiple factors on carbon emissions, this paper uses three traditional single-item carbon emission prediction models of Support Vector Regression, Ridge Regression and BP Neural Network and combines with the inverse of the error method to construct a variable weight combination model, and uses the new model to predict Chinas carbon emissions from 2022 to 2026. The empirical results show that the fitting and prediction accuracy of the combination model is 99.26% and 99.34%, respectively, and the combination model has higher accuracy than the three single models. The prediction results of the combination model show that by 2026, the growth rate of Chinas carbon emissions has slowed down compared with the present, and maintains the growth rate at 1.8%.
Keywords: Support Vector Regression; Ridge Regression; BP Neural Network; variable weight combination model
0" 引" 言
伴随着温室效应的影响日渐加重,人们对温室气体特别是二氧化碳的关注度持续升高,为了更有效地应对全球气候变暖的挑战,各国学者正不断地进行研究和讨论,旨在探索对碳排放进行准确预测的方法,希望能够为减少温室气体排放提供有价值的见解和建议。对于碳排放量的预测,国内外的学者们采用了多种模型来进行研究。赵息等[1]利用离散二阶差分算法预测了中国2020年的碳排放量;王宪恩等[2]基于可扩展的STIRPAT模型,结合情景分析预测吉林省将在2029—2045年达到碳达峰。王利兵和张赟[3]利用STIRPAT模型,结合情景分析法,在低碳、中碳、高碳三种情景之下,对我国2025—2030年的能源碳排放量进行预测,结果表明我国有望在2029年实现碳达峰;Tang等[4]利用GM(1,1)和多项式回归对江苏省的碳排放量进行了预测;Wen和Yuan[5]利用BP神经网络来进行碳排放量的预测,结果显示预测精度为98.73%;金尚柱和李青霞[6]利用支持向量回归机模型对重庆市碳排放量进行预测,结果显示重庆市2025—2030年碳排放量年减少率约为0.9%。上述文献中,碳排放量的预测模型一般是单个模型。随着研究的深入,国内外学者发现通过将线性模型和非线性模型的单个模型组合,能更好地发挥各单项模型的优点,有效地从原始数据中提取出更多的信息,从而提高模型预测的准确性。卢奇等[7]通过将GM(1,1)、神经网络和多元线性回归结合,构建了一个组合模型,用于预测我国能源消耗,研究结果证明组合模型预测更为有效;罗曼等[8]采用了ARIMA时间序列模型、NAR神经网络、STIRPAT模型,构建组合模型来预测萧山地区的碳排放量,结果显示组合模型相比各单一模型精度更高;张新红和王瑞晓[9]选取逻辑回归模型和径向基函数(RBF)神经网络模型,构建了一种用于信用风险预警的组合模型,结果表明组合模型可以达到更好的预期效果。吕欣曼等[10]利用OGM(1,N)、BP神经网络和偏最小二乘回归构建一种变权组合模型,结果显示组合模型较各单项模型有更高的预测精度。权重的选择对于组合模型的预测效果起着决定性作用。根据权重选择方式的不同,组合模型主要分为两种类型:固定权重组合模型和可变权重组合模型。张鹏[11]通过比较分析发现,相较于固定权重组合模型,可变权重组合模型更能适应更实际需求。刘东君和邹志红[12]通过最小化误差平方和来确定模型的权重。
在上述研究的基础上,本文基于支持向量机回归、岭回归和BP神经网络,利用误差倒数法构造变权组合模型,并利用其对我国2022—2026年的碳排放量进行预测。
1" 组合预测模型以及权重的计算
1.1" 组合预测模型的构建
在进行问题预测时,如果采用了n个独立的预测模型,其中每个模型的预测结果用yi来表示,每个模型都有一个相对应的权重系数wi,其中i = 1,2,…,n,那么,基于这n个独立模型构建的组合预测模型可以表示为:
1.2" 基于误差倒数法的权重计算
为了使得组合预测模型的准确性更高,本文在计算各单项模型权重的基本思想是预测误差平方和越大的单项模型在组合模型中所占的权重系数越小,各个模型的权重系数使用误差倒数法来进行计算。这种方法基于这样一个原理:每个独立模型的权重系数由其总误差平方和的倒数与所有模型总误差平方和倒数之和的比例来确定。误差倒数法有两个优点,一是赋予误差较小的单项模型更大的权重,提高组合模型的预测精度;二是保证模型权重非负。
ei = (yi-y)2表示第i种单项预测模型的总误差平方和,则该模型的权重可表示为:
考虑到总误差平方和小并不能保证每一年的误差平方和较小,因而本文在计算各单项模型的权重时,在每一年分别计算各单项模型的权重,构建变权组合模型。
eit=(yit-yt)2表示第i种模型t时刻的预测误差平方,则在样本期内t时刻该模型的权重表示为:
其中m表示观察时刻的个数。
2" 单项模型预测
2.1" 支持向量机回归
支持向量机回归(Support Vector Regression, SVR)是支持向量机(Support Vector Machine, SVM)技术的延伸,用于解决回归问题。与传统的回归分析相比,SVR采用了一种非线性转换,将原始数据投影到一个更高维度的特征空间。在这个高维空间中,原本可能复杂的非线性关系可以表现为简单的线性关系。SVR正是利用这一特性,在高维特征空间中建立线性回归模型,然后再将得到的模型转换回原始数据空间,通过最小化预测结果与实际结果之间的差异,同时考虑到支持向量与超平面之间的最大间隔,从而实现回归任务。
2.2" 岭回归模型
回归模型是一种预测性模型,研究的是因变量和自变量之间的关系。考虑到回归模型中选取的自变量可能会存在多重共线性,而岭回归作为一种处理共线性数据的回归方法,可以通过损失部分信息消除变量之间的多重共线性,得到更为可靠的结果,同时考虑数据的异方差性以及量纲的影响,因而本文选择使用岭回归建立双对数线性回归模型,模型如下:,其中表示选取的自变量。
2.3" BP神经网络
BP神经网络是一种依照误差逆向传播训练的多层前馈神经网络,它包含输入层、隐含层、输出层,每层又包含若干个神经元。BP神经网络包括两个过程,一是信号的前向传播,二是误差的反向传导。输入信号通过隐含层的激活函数变换传递到输出层,若实际输出与预期输出不符合,再进行反向传导。通过正向和反向传播的不断循环,达到最小误差时停止训练。BP神经网络的一个优点是具有很强的非线性映射能力,因而在非线性预测领域应用十分广泛。
3" 实证分析
3.1" 数据来源
本文基于已有研究,综合考虑二氧化碳排放量的影响因素,最终选取人均国内生产总值、城镇化率、能源强度、能源结构为主要影响因素。数据来源于《BP世界能源统计年鉴》和《中国统计年鉴》,数据收集截止到2021年。
3.2" 模型实证
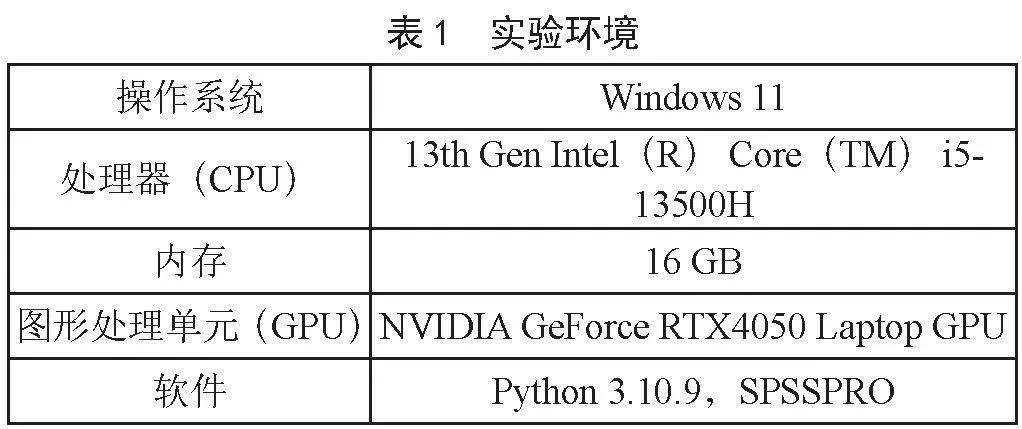
本次研究,选取2008—2016年期间的二氧化碳排放量及其相关影响因素作为建模数据。随后,为了检验模型的预测能力,使用2017—2021年的数据对所有单独的预测模型以及组合模型进行了测试和评估,实验环境如表1所示,
3.2.1" 支持向量机回归实证结果
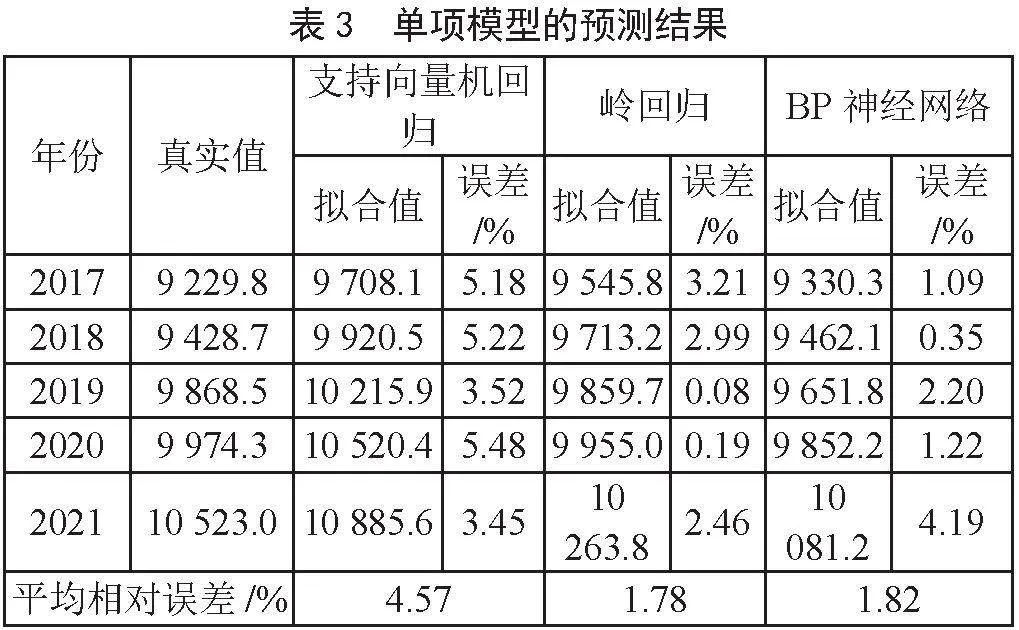
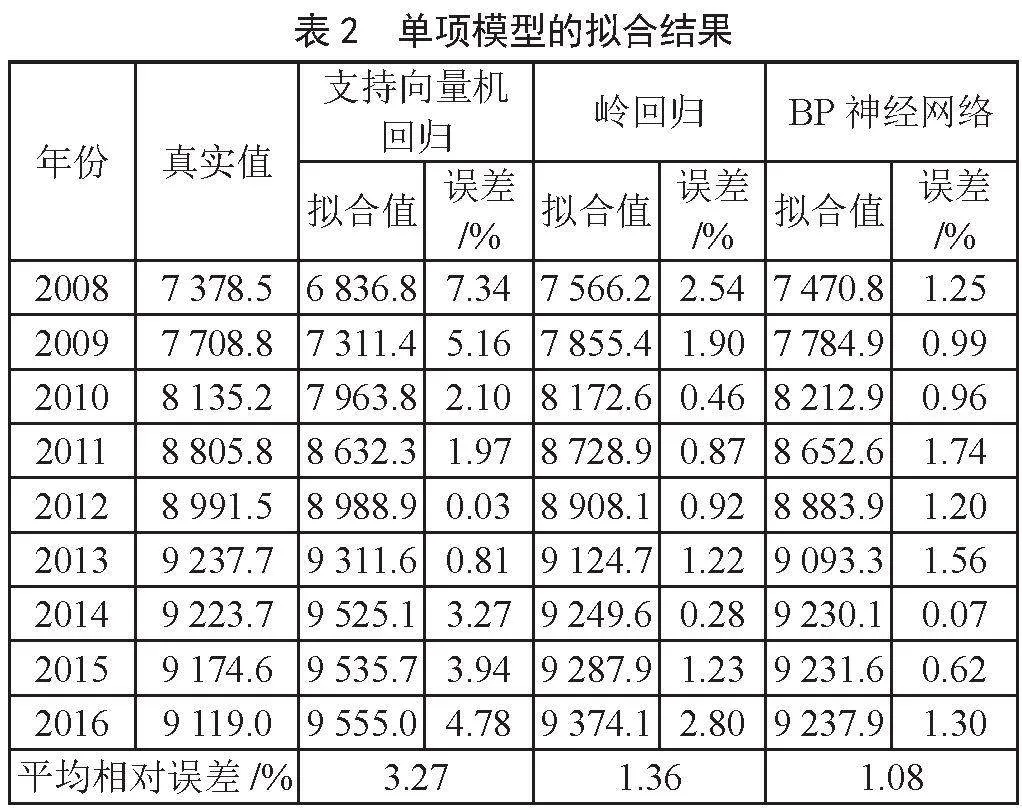
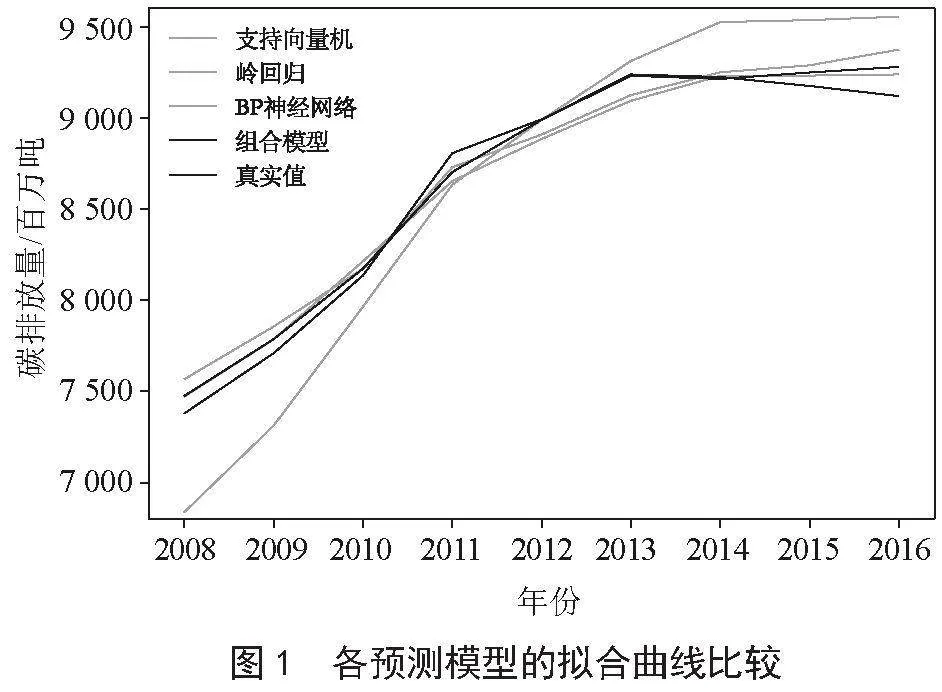
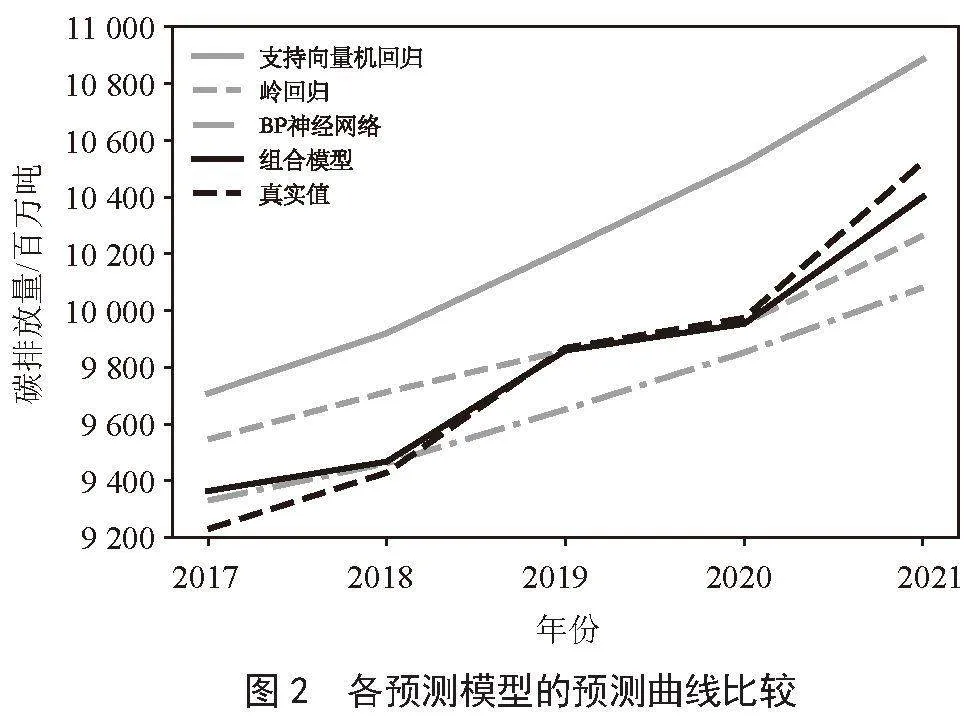
使用支持向量机回归模型对2008—2016年的碳排放量数据进行拟合,得到了2017—2021年的碳排放量数据的预测值,模型拟合效果如图1所示,预测结果如图2所示。随后对模型的拟合相对误差和预测相对误差进行计算,结果如表2和表3所示。
3.2.2" 岭回归实证结果
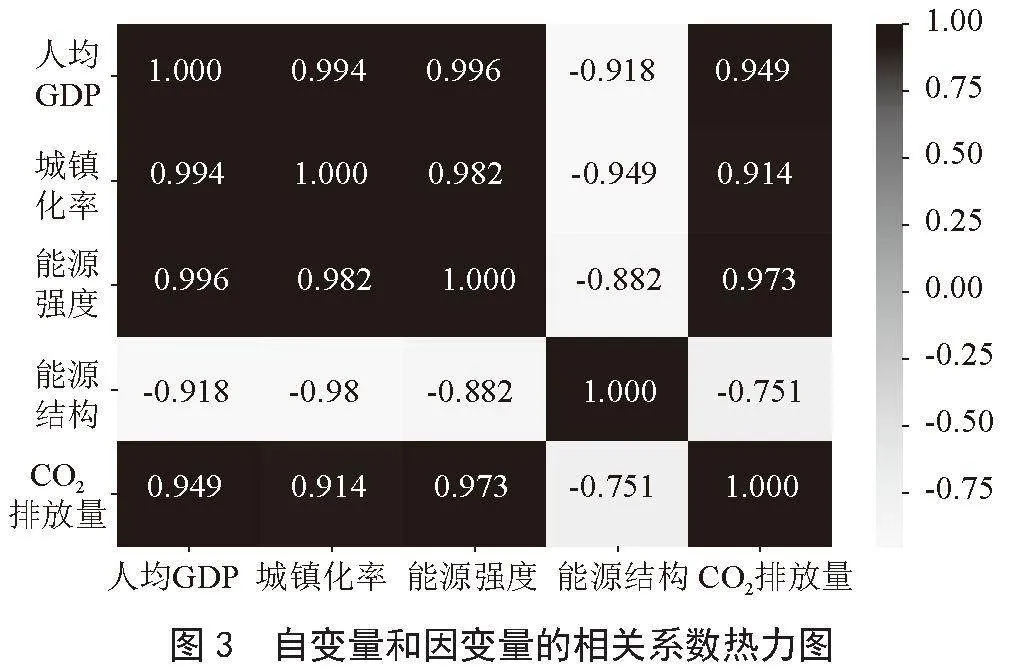
为了解决数据的异方差并消除量纲差异的影响,选择采用双对数岭回归模型预测碳排放量数据。在对原始数据进行转换之后,计算因变量与自变量之间的相关系数,相关系数如图3所示。
由图3可知,自变量之间的相关性很强,模型的预测效果会受到影响,为了消除多重共线性的影响,提高模型的精度,选择使用岭回归模型。最后得到的岭回归预测方程为;
其中x1表示能源结构,x2表示能源强度,x3表示城镇化率,x4表示人均GDP。
3.2.3" BP神经网络实证结果
本次研究采用三层BP神经网络模型来进行预测分析,其中激活函数选择ReLU函数。鉴于碳排放量预测涉及4个自变量,因而输入层神经元个数为4,输出层神经元个数为1。对于隐藏层的神经元数量,按照公式s = 2n+1(s表示隐含层神经元个数,n表示输入层神经元个数)的关系来计算,计算得出隐藏层神经元个数为9,同时设置学习率为0.05,最大训练迭代次数为10 000。拟合2008—2016年的数据,预测了2017—2021年的碳排放量,模型拟合效果如图1所示,预测结果如图2所示,随后对模型的拟合相对误差和预测相对误差进行计算,结果如表2和表3所示。
3.2.4" 组合模型预测结果
对比三种单项模型的实证结果可以发现,三种模型对碳排放量的结果预测各有优劣。比如BP神经网络模型在对数据进行拟合时,平均相对误差最小,而岭回归模型在对数据进行预测时,平均相对误差最小。实证结果表明,不同的预测模型适用性不同,因此考虑使用组合模型来消除各单项模型的劣势,提高模型的预测精度。
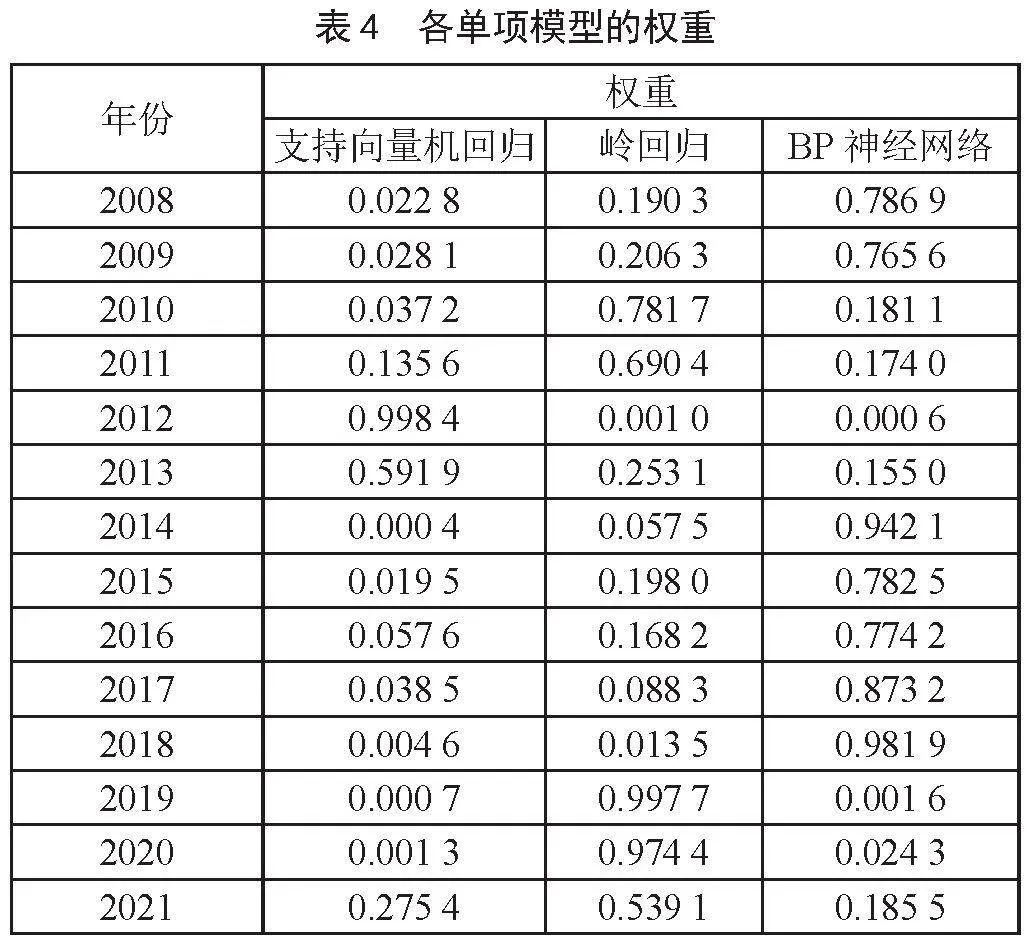
在基于误差平方和确定各模型的权重时,通常的做法是将更大的权重赋予误差更小的模型,将较小的权重赋予误差较大的模型。根据方差倒数法计算各单项模型的权重,计算结果如表4所示。
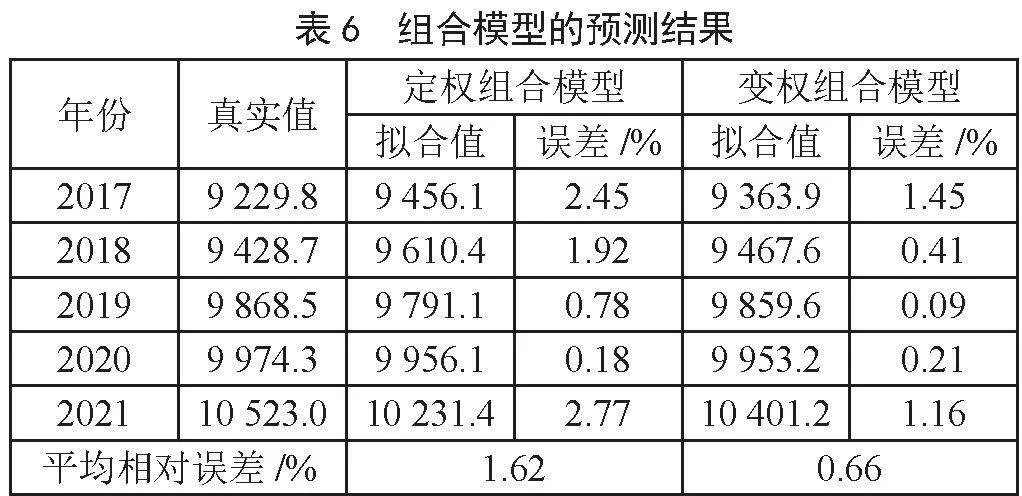
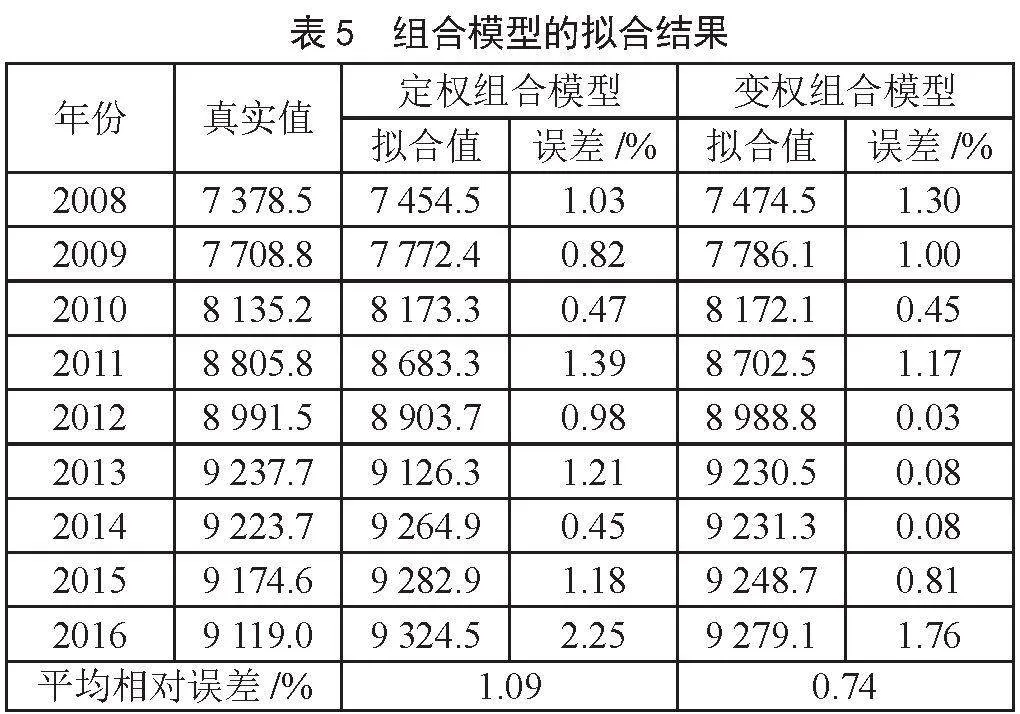
根据各单项模型的权重,可以计算得到组合模型的结果。组合模型拟合效果如图1所示,预测结果如图2所示,计算的拟合相对误差和预测相对误差如表5,表6所示。
为了说明变权组合模型相较定权组合模型的优势,本文同时根据误差倒数法构建定权组合模型。计算得到支持向量机回归模型、岭回归模型、BP神经网络模型的权重分别为0.089 9,0.426 3,0.483 8,得到组合模型的拟合结果和预测结果如表5,表6所示。
3.2.5" 模型的比较
根据三种单项模型以及两种组合模型的结果可以发现,变权组合模型的拟合平均相对误差和预测平均相对误差分别为0.74%和0.66%,相较三种单项模型和定权组合模型,变权组合模型的精度更高。结果表明,利用误差倒数法构建的变权组合模型对中国碳排放量预测是有效的。
3.3" 未来趋势预测
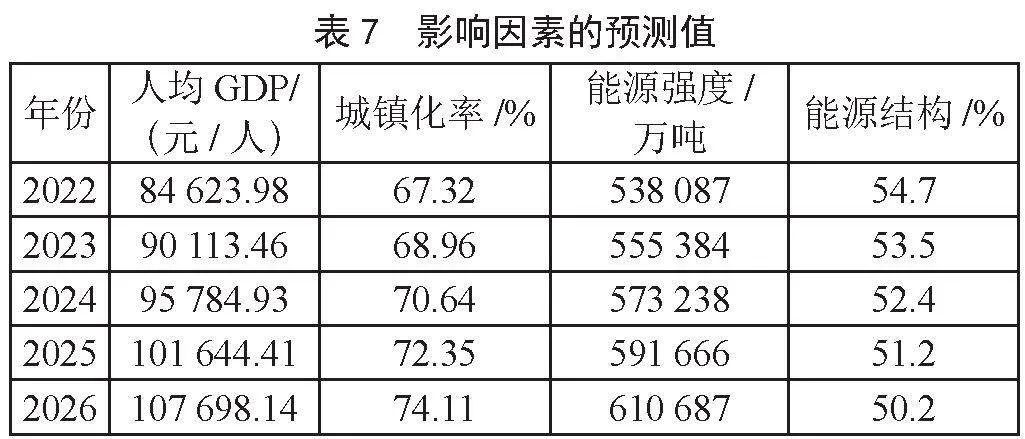
3.3.1" 影响因素的预测值
考虑到常用的情景分析预测法主观性较强,本文决定利用灰色模型预测4个影响因素未来的数据,选取2008—2021年的数据来预测2022—2026年的数据,数据如表7所示。
3.3.2" 碳排放量的预测
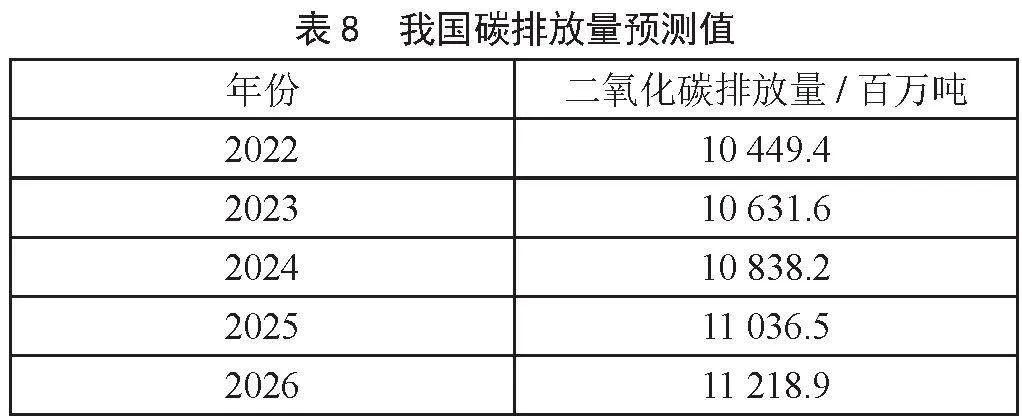
根据表6数据,采用变权组合模型对中国2022—2026年的碳排放量进行了预测。由于未来的实际值是未知的,因此先对三种单项模型赋予相同的权重,利用组合模型计算预测值,然后将此值作为实际值再计算各单项模型的权重,将权重重新变换后计算的值作为最终的预测值,最终预测结果如表8所示。
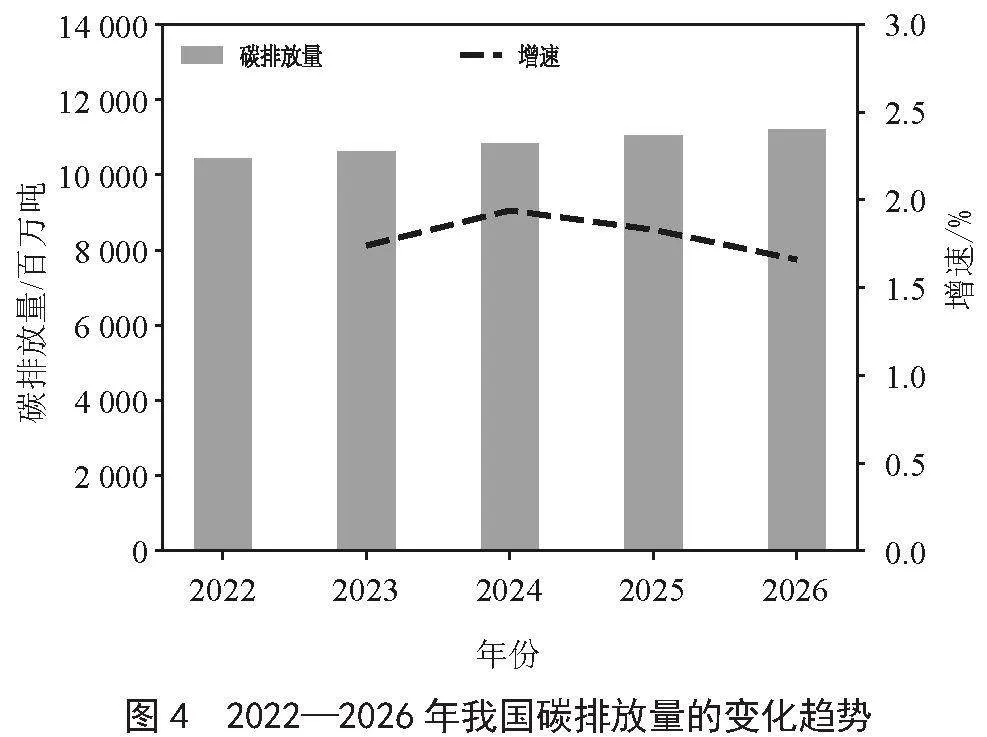
根据预测值,绘制了2022—2026年我国碳排放量的变化趋势图,如图4所示。
从图4可以看出,未来几年我国碳排放量依然会维持一个增长的趋势,预计2026年,我国的碳排放量将达到112.2亿吨,未来碳排放量的平均增速约为1.8%,与之相比较的我国最近五年碳排放量的平均增速约为3%,碳排放量的增长速度明显放缓并且呈下降趋势,说明在双碳目标的背景下,我国的低碳发展已经初步取得了成效,我国有望在2030年实现碳达峰目标。
4" 结" 论
碳排放量的预测一般使用单项模型,但是考虑到不同的单项模型的适用性不同,单一的模型可能无法反映原始数据的全部信息,影响预测结果。所以利用组合模型来弥补单项模型的缺点,从而提高模型预测效果。
本文在支持向量机回归、岭回归和BP神经网络等单项模型的基础上,利用误差倒数法构建了一种变权组合模型,并利用组合模型对我国2022—2026年碳排放量进行预测。实证结果显示组合模型相较于单项模型精度更高,为碳排放预测模型提供了新的思路,预测结果显示未来几年我国低碳发展取得成效,碳排放量的年增长速率大约维持在1.8%,较目前有所减缓。
参考文献:
[1] 赵息,齐建民,刘广为.基于离散二阶差分算法的中国碳排放预测 [J].干旱区资源与环境,2013,27(1):63-69.
[2] 王宪恩,史记,王泳璇,等.吉林省能源消费碳排放变化趋势预测与影响因素分析 [J].环境科学与技术,2015,38(6):247-251.
[3] 王利兵,张赟.中国能源碳排放因素分解与情景预测 [J].电力建设,2021,42(9):1-9.
[4] TANG D C,MA T Y,LI Z J,et al. Trend Prediction and Decomposed Driving Factors of Carbon Emissions in Jiangsu Province during 2015—2020 [J].Sustainability,2016,8(10):1-15.
[5] WEN L,YUAN X Y. Forecasting CO2 Emissions in Chinas Commercial Department, through BP Neural Network Based on Random Forest and PSO [J].Science of the Total Environment,2020(718):137194.
[6] 金尚柱,李青霞.基于支持向量回归机的重庆市碳排放量预测研究 [J].重庆科技学院学报:自然科学版,2022,24(1):110-114.
[7] 卢奇,顾培亮,邱世明.组合预测模型在我国能源消费系统中的建构及应用 [J].系统工程理论与实践,2003(3):24-30.
[8] 罗曼,余彬,翁利国,等.基于组合预测模型的萧山碳排放预测 [J].节能,2022,41(4):75-80.
[9] 张新红,王瑞晓.我国上市公司信用风险预警研究 [J].宏观经济研究,2011(1):50-54.
[10] 吕欣曼,殷克东,李雪梅.灰色多元变权组合预测模型及其应用 [J].统计与决策,2022,38(14):25-29.
[11] 张鹏.组合预测中变权与定权的应用比较 [J].统计与决策,2018,34(17):80-82.
[12] 刘东君,邹志红.最优加权组合预测法在水质预测中的应用研究 [J].环境科学学报,2012,32(12):3128-3132.