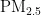
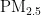
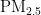
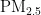
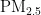
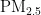
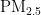
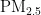
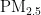
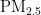
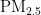
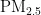
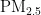
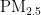
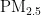
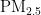
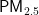
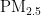
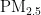
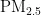
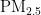
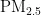
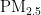
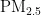
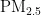
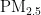
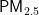
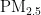
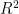
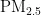
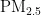
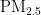
关键词: 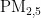 浓度;预测模型;PSO算法;BP神经网络
浓度;预测模型;PSO算法;BP神经网络
中图分类号:TP391.4;TP183 文献标识码:A 文章编号:2096-4706(2025)07-0047-06
Abstract:Aimingat the problem thatthe traditional BPNeural Network has slowconvergence speedand iseasyto fall into local optimal solution, this paper proposes a 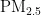 concentration prediction model based on Particle Swarm Optimization (PSO)algorithmoptimizedBPNeuralNetwork,whichcanquicklyconvergeandgettheglobal optimalsolution.Firstly,the pollutant indexes with high correlation with
concentration prediction model based on Particle Swarm Optimization (PSO)algorithmoptimizedBPNeuralNetwork,whichcanquicklyconvergeandgettheglobal optimalsolution.Firstly,the pollutant indexes with high correlation with 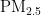 concentration are selected as input variables by Pearson correlation analysis. Secondly,thePSOalgorithmisusedtooptimizetheinitialweightsandthresholdsofBPNeuralNetwork,whichovercomesthe shortcomingsofBPNeuralNetwork,suchaseasytofallintolocaloptimumandslowconvergencespeed.Finally,themodel is trained and tested using air pollutant data from July 2O21 to June 2024 in Chengdu.Theresults show that the
concentration are selected as input variables by Pearson correlation analysis. Secondly,thePSOalgorithmisusedtooptimizetheinitialweightsandthresholdsofBPNeuralNetwork,whichovercomesthe shortcomingsofBPNeuralNetwork,suchaseasytofallintolocaloptimumandslowconvergencespeed.Finally,themodel is trained and tested using air pollutant data from July 2O21 to June 2024 in Chengdu.Theresults show that the 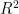 of the test setis 0.944,theMAEofthetestsetis4.231,andtheRMSEofthetestsetis6.364.ComparedwiththeunoptimizedBPNeural Network model,thePO-BPmodelhashgherpredictionaccuracyandfasterconvergencespeed,andcaneffctivelyprdictthe
of the test setis 0.944,theMAEofthetestsetis4.231,andtheRMSEofthetestsetis6.364.ComparedwiththeunoptimizedBPNeural Network model,thePO-BPmodelhashgherpredictionaccuracyandfasterconvergencespeed,andcaneffctivelyprdictthe 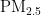 concentration of the next day in Chengdu.
concentration of the next day in Chengdu.
Keywords: 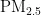 concentration,prediction model,PsO algorithm,BPNeural Network
concentration,prediction model,PsO algorithm,BPNeural Network
0 引言
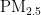 ,即细颗粒物,其尺寸微小且具有强烈的吸附能力,它们在大气中停留时间长,能远距离传输,并可通过呼吸深入人体肺部和血液[1]。这些颗粒物含有的重金属等有毒物质,会对呼吸系统、免疫系统和循环系统造成破坏,引发呼吸道疾病、心血管疾病,乃至肺癌等严重健康问题[2-3]。随着工业化和城市化进程的加快,空气污染问题日益严重,
,即细颗粒物,其尺寸微小且具有强烈的吸附能力,它们在大气中停留时间长,能远距离传输,并可通过呼吸深入人体肺部和血液[1]。这些颗粒物含有的重金属等有毒物质,会对呼吸系统、免疫系统和循环系统造成破坏,引发呼吸道疾病、心血管疾病,乃至肺癌等严重健康问题[2-3]。随着工业化和城市化进程的加快,空气污染问题日益严重, 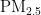 作为主要污染物之一,其直径越小,对人体和环境的危害越大[4。特别是在人口密集和经济发达地区,
作为主要污染物之一,其直径越小,对人体和环境的危害越大[4。特别是在人口密集和经济发达地区, 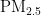 对人体健康的影响尤为显著[5]。因此,建立一个能够准确预测
对人体健康的影响尤为显著[5]。因此,建立一个能够准确预测 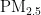 浓度的模型,对于大气污染防治和实现可持续发展至关重要。随着经济的增长,环境污染问题也日益凸显。汽车尾气、工业排放和取暖排放等活动导致空气中
浓度的模型,对于大气污染防治和实现可持续发展至关重要。随着经济的增长,环境污染问题也日益凸显。汽车尾气、工业排放和取暖排放等活动导致空气中 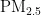 浓度增加,进而引发肺部疾病和心脑血管疾病,对人类健康构成威胁[2,5]。精准的
浓度增加,进而引发肺部疾病和心脑血管疾病,对人类健康构成威胁[2,5]。精准的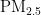 浓度预测对于提前采取防护措施、保护人类健康具有重要意义。本研究旨在通过粒子群优化 (PSO)算法优化的BP神经网络,提高
浓度预测对于提前采取防护措施、保护人类健康具有重要意义。本研究旨在通过粒子群优化 (PSO)算法优化的BP神经网络,提高 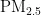 浓度预测的准确性,为环境管理提供科学依据,以减轻
浓度预测的准确性,为环境管理提供科学依据,以减轻 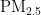 对公共健康的影响。
对公共健康的影响。
在环境科学和人工智能交叉的研究领域中,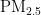 浓度预测对空气质量和人类健康有着显著影响,因此受到了众多学者的广泛关注[6-12]。张丹宁等[提出了基于BP神经网络的
浓度预测对空气质量和人类健康有着显著影响,因此受到了众多学者的广泛关注[6-12]。张丹宁等[提出了基于BP神经网络的 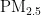 浓度预测模型,该模型利用西安市的大气污染物监测数据进行训练学习,并用后续数据进行测试和检验,建立了精度较高的
浓度预测模型,该模型利用西安市的大气污染物监测数据进行训练学习,并用后续数据进行测试和检验,建立了精度较高的 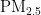 浓度预测模型,有效预测次日
浓度预测模型,有效预测次日 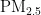 浓度值,并针对偏差较大的预测结果进行了成因分析和讨论。邸鹏等则基于BP神经网络建立了北京市
浓度值,并针对偏差较大的预测结果进行了成因分析和讨论。邸鹏等则基于BP神经网络建立了北京市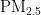 浓度预测模型,通过高精度拟合的BP网络预测模型,反映了北京市雾霾天气状况,为空气质量监测和预报提供了参考。彭豪杰等[1综合考虑深度学习与随机森林的特点,提出了基于深度学习与随机森林的
浓度预测模型,通过高精度拟合的BP网络预测模型,反映了北京市雾霾天气状况,为空气质量监测和预报提供了参考。彭豪杰等[1综合考虑深度学习与随机森林的特点,提出了基于深度学习与随机森林的 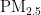 浓度预测组合模型,该模型在较少数据情况下具有较好的预测精度,尤其是在使用LSTM作为特征选择器、RF为回归器的组合模型中表现最优。张旭等提出了改进的PSO-GA混合算法对BP神经网络的初始权值和阈值进行设定,有效避免了陷入局部极小,提高了收敛速度,仿真结果表明改进的模型比PSO-BP预测模型收敛性更好。胡俊等建立了基于改进人工蜂群BP神经网络的
浓度预测组合模型,该模型在较少数据情况下具有较好的预测精度,尤其是在使用LSTM作为特征选择器、RF为回归器的组合模型中表现最优。张旭等提出了改进的PSO-GA混合算法对BP神经网络的初始权值和阈值进行设定,有效避免了陷入局部极小,提高了收敛速度,仿真结果表明改进的模型比PSO-BP预测模型收敛性更好。胡俊等建立了基于改进人工蜂群BP神经网络的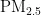 质量浓度预测模型,通过优化人工蜂群算法的寻优精度与收敛速率,提升了模型的稳定性和预测精准性。
质量浓度预测模型,通过优化人工蜂群算法的寻优精度与收敛速率,提升了模型的稳定性和预测精准性。
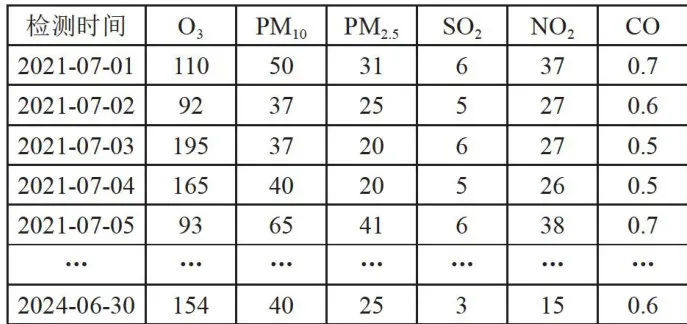 表1原始实验数据
表1原始实验数据
这些研究表明,尽管已有多种方法被提出以提高  浓度预测的准确性,但仍需进一步优化算法以增强模型的泛化能力和适应性,特别是在数据量较少或数据存在缺失时的预测性能。本研究旨在通过改进PSO算法优化BP神经网络,提高
浓度预测的准确性,但仍需进一步优化算法以增强模型的泛化能力和适应性,特别是在数据量较少或数据存在缺失时的预测性能。本研究旨在通过改进PSO算法优化BP神经网络,提高  浓度预测的准确性和鲁棒性,从而为大气污染防治提供更为可靠的决策支持。
浓度预测的准确性和鲁棒性,从而为大气污染防治提供更为可靠的决策支持。
1数据来源和分析
1. 1 数据来源
本研究选取四川省成都市作为研究对象,数据来源为四川省生态环境厅官方网站(https://sthjt.sc.gov.cn/sthjt/sjxz/list_w.shtml),涵盖了2021年7月至2024年6月期间的逐日大气污染物监测数据。研究涉及的污染物包括 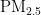 ,
, 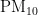 ,
, 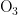 、
、 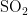 、CO和
、CO和 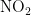 等关键指标,旨在通过这些数据预测成都市次日的
等关键指标,旨在通过这些数据预测成都市次日的 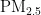 浓度值,为居民出行和健康防护提供科学依据。原始实验数据如表1所示。
浓度值,为居民出行和健康防护提供科学依据。原始实验数据如表1所示。
1.2 数据分析
为了降低模型预测误差,在模型构建之前,对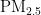 浓度与其他大气污染物浓度进行了相关性分析。在本研究中,我们采用了皮尔逊相关性系数进行分析。计算式为:
浓度与其他大气污染物浓度进行了相关性分析。在本研究中,我们采用了皮尔逊相关性系数进行分析。计算式为:
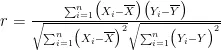
其中, r 为相关系数, n 为样本总数, X 和 Y 为两个变量, X 和 Y 分别为它们的均值。 Ψ, r 的取值范围在-1到1之间,其绝对值越接近1,表明变量间的线性关系越强。通过此分析,我们能够量化 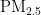 与其他污染物之间的相关性,为BP神经网络模型的输入变量选择提供依据。
与其他污染物之间的相关性,为BP神经网络模型的输入变量选择提供依据。
2 研究方法
2.1模型及算法原理
本研究构建的BP(BackPropagation)神经网络模型,旨在预测 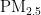 浓度,包含输入层、隐藏层和输出层。输入层接收经预处理的数据,隐藏层进行特征提取与非线性映射,输出层则产生预测结果。模型通过前向传播和反向传播机制进行学习与调整,其中误差通过反向传播修正网络的权重和偏置,直至达到预定的误差阈值[13]。选择合适的隐藏层神经元数量是关键,过多或过少均会影响模型性能。本研究依据经验式(2)确定隐藏层神经元数目,确保模型既能捕捉数据的复杂性,又避免过拟合或欠拟合。
浓度,包含输入层、隐藏层和输出层。输入层接收经预处理的数据,隐藏层进行特征提取与非线性映射,输出层则产生预测结果。模型通过前向传播和反向传播机制进行学习与调整,其中误差通过反向传播修正网络的权重和偏置,直至达到预定的误差阈值[13]。选择合适的隐藏层神经元数量是关键,过多或过少均会影响模型性能。本研究依据经验式(2)确定隐藏层神经元数目,确保模型既能捕捉数据的复杂性,又避免过拟合或欠拟合。
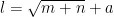
其中,1为隐藏层的节点数, m 为输入层的节点数,n 为输出层的节点数, a 为一个介于1到10之间的常数,用于调整隐藏层的节点数。
粒子群优化(particle swarmoptimization,PSO)算法是一种模拟鸟群社会行为的群体智能技术,用于解决复杂的优化问题[14]。该算法通过模拟鸟群捕食行为,让群体中的粒子在搜索空间中通过个体和群体经验协同搜索最优解。每个粒子根据自身经验和群体经验动态调整位置和速度,以探索潜在的解空间。假设有一个 d 维的目标搜索空间当中共有 m 个粒子,其中第 i 个粒子的位置和速度都是 d 维的空间向量 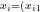 ,
, 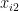 ,…,
,…, 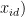 和
和 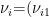 ,
, 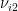 ,…,
,…, 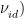 ,其中 i=1 ,2,…, ∇m 。每一次迭代后,速度和位置更新分别为:
,其中 i=1 ,2,…, ∇m 。每一次迭代后,速度和位置更新分别为:
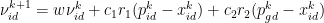
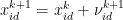
其中, 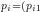 ,
, 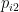 ,…,
,…, 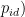 为第 i 个粒子目前搜索到的最优位置,
为第 i 个粒子目前搜索到的最优位置, 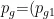 ,
, 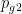 ,…,
,…, 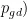 为目前整个粒子群搜索到的最优位置。
为目前整个粒子群搜索到的最优位置。 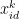 和
和 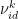 为第 i 个粒子在第k 次迭代飞行和第 i 维的位置和速度分量,
为第 i 个粒子在第k 次迭代飞行和第 i 维的位置和速度分量, 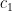 ,
, 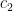 为粒子的学习因子,
为粒子的学习因子, 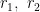 为[0,1]之间随机数, w 为惯性权重。这些更新规则确保粒子在保持多样性的同时,能够有效地向最优解靠近。通过迭代更新,PSO算法能够平衡全局搜索和局部搜索的能力,从而在多维空间中找到问题的最优或近似最优解。在本研究中,PSO算法被用于优化BP神经网络的参数,以提高
为[0,1]之间随机数, w 为惯性权重。这些更新规则确保粒子在保持多样性的同时,能够有效地向最优解靠近。通过迭代更新,PSO算法能够平衡全局搜索和局部搜索的能力,从而在多维空间中找到问题的最优或近似最优解。在本研究中,PSO算法被用于优化BP神经网络的参数,以提高 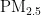 浓度预测的准确性和效率。
浓度预测的准确性和效率。
2.2 模型构建
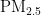 浓度预测模型的构建如图1所示。首先,对获取的原始数据进行相关性分析,以降低模型的预测误差。为了加快学习算法的收敛速度,然后将数据进行归一化处理,并将数据划分为训练集和测试集。在模型构建中,首先确定BP神经网络的层数及每层所需的神经元个数。为了提高收敛速度和精度,采用PSO算法优化BP神经网络的初始权重和阈值,具体优化流程如图2所示。然后,使用训练集构建
浓度预测模型的构建如图1所示。首先,对获取的原始数据进行相关性分析,以降低模型的预测误差。为了加快学习算法的收敛速度,然后将数据进行归一化处理,并将数据划分为训练集和测试集。在模型构建中,首先确定BP神经网络的层数及每层所需的神经元个数。为了提高收敛速度和精度,采用PSO算法优化BP神经网络的初始权重和阈值,具体优化流程如图2所示。然后,使用训练集构建 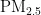 的预测模型,最后使用测试集来预测次日的
的预测模型,最后使用测试集来预测次日的 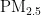 浓度。
浓度。
2.3 评价指标
在本研究中,我们采用均方根误差(RMSE)、决定系数 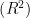 )和平均绝对误差(MAE)作为评价BP神经网络模型预测
)和平均绝对误差(MAE)作为评价BP神经网络模型预测 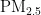 浓度精度的指标。具体计算式如式(5)至式(7)所示。
浓度精度的指标。具体计算式如式(5)至式(7)所示。
均方根误差(RMSE)衡量预测值与实际值偏差的平方和的平均数的平方根,公式为:
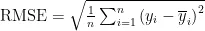
决定系数 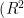 )反映模型对数据的拟合程度,公式为:
)反映模型对数据的拟合程度,公式为:
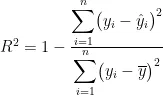
平均绝对误差(MAE)衡量预测值与实际值绝对偏差的平均值,公式为:
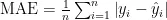
其中, 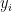 为实际观测值,
为实际观测值, 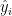 为预测值,
为预测值, 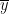 为实际观测值的平均值。这些指标综合评估模型的预测性能,RMSE和MAE越低表示预测误差越小,
为实际观测值的平均值。这些指标综合评估模型的预测性能,RMSE和MAE越低表示预测误差越小, 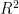 越接近1表示模型拟合度越好。
越接近1表示模型拟合度越好。
3 实验及结果分析
3.1 实验环境和设置
在实验中,操作系统环境是macOSSonoma14.6.1版本,处理器是AppleM1Pro,仿真平台是MATLABR2021b。实验过程如下:首先,本次数据选取成都市2021年7月至2024年6月的零时刻逐日数据,经过缺失值处理后,共计1087个样本。采用皮尔逊相关系数衡量指标间的线性关系,并通过双尾检验来确定 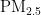 与其他指标的相关性是否显著;然后将数据划分为训练集和测试集,比例为8:2,分别对训练集和测试集进行mapminmax(归一化处理,将其归一化到[0,1]区间,得到无量纲数据,从而提升网络的收敛速度。
与其他指标的相关性是否显著;然后将数据划分为训练集和测试集,比例为8:2,分别对训练集和测试集进行mapminmax(归一化处理,将其归一化到[0,1]区间,得到无量纲数据,从而提升网络的收敛速度。
构建网络:对于 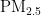 浓度预测,输入维度为5个,分别是
浓度预测,输入维度为5个,分别是 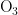 ,
, 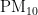 ,
, 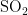 、
、 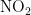 、CO,输出维度为
、CO,输出维度为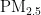 。因此,输入和输出神经元的节点数分别为5和1。再根据经验公式
。因此,输入和输出神经元的节点数分别为5和1。再根据经验公式 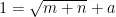 ,其中
,其中 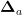 是[0,10]之间的常数,得到隐藏层节点数为5,从而BP神经网络结构为5-5-1。然后设置网络的超参数:最大训练次数为 1 0 0 0 ,目标误差为
是[0,10]之间的常数,得到隐藏层节点数为5,从而BP神经网络结构为5-5-1。然后设置网络的超参数:最大训练次数为 1 0 0 0 ,目标误差为 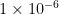 ,学习率为0.01。
,学习率为0.01。
为了加快网络收敛速度并防止陷入局部最优,对于本文提出的PSO-BP预测模型,粒子群参数设置如下:种群规模 S=5 0 ,惯性权重最大值 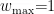 ,最小值
,最小值 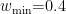 ,两个学习因子
,两个学习因子 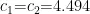 ,粒子位置范围[-1,1],速度范围[-1,1]。
,粒子位置范围[-1,1],速度范围[-1,1]。
3.2 实验结果与讨论
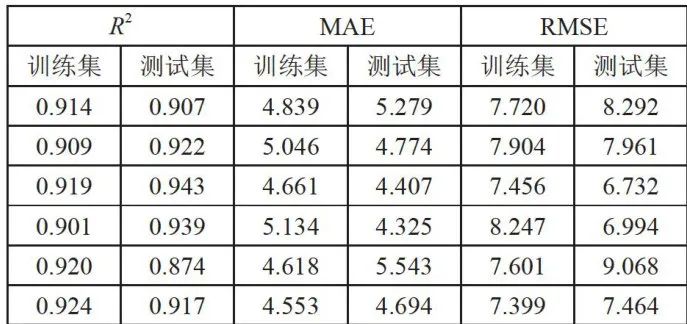
根据表2所示的实验结果,将经过预处理的数据输入到PSO优化的BP神经网络模型中,经过10次随机实验,模型在测试集上展现了较高的预测精度。具体而言,测试集的 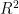 值达到0.944,表明模型解释了 9 4 . 4 % 的方差,显示出较强的解释能力。同时,测试集的平均绝对误差(MAE)为4.231,均方根误差(RMSE)为6.364,这些指标均表明模型具有较高的预测精度和较低的误差水平。结果表明,该模型在
值达到0.944,表明模型解释了 9 4 . 4 % 的方差,显示出较强的解释能力。同时,测试集的平均绝对误差(MAE)为4.231,均方根误差(RMSE)为6.364,这些指标均表明模型具有较高的预测精度和较低的误差水平。结果表明,该模型在 浓度预测任务中具有良好的拟合度和稳定性,为环境监测提供了一个有效的工具。
浓度预测任务中具有良好的拟合度和稳定性,为环境监测提供了一个有效的工具。
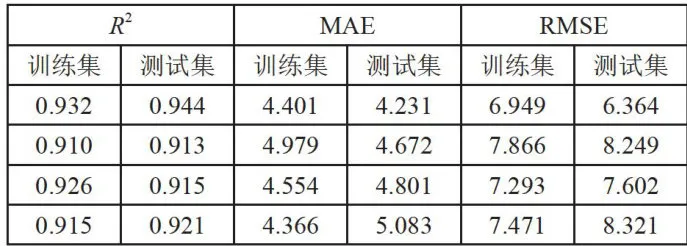 表2指标统计结果
表2指标统计结果(续表)
为了验证模型的拟合度,实验分别在训练集、验证集、测试集以及整体数据集上进行仿真。从图3可以看出,模型在训练集( 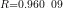 、验证集( ⋅ - 0 . 9 8 0 38)、测试集( R=0 . 9 7 3 8 8 )以及整体数据集( ( R = 0 . 9 6 5 24)上均展现出了较高的相关系数(R值),这表明模型具有很好的拟合能力。图中的拟合线(FT)与理想线( Y = T )非常接近,进一步证实了模型预测值与实际值之间的高度一致性。此外,输出方程中的常数项(0.017至0.014)表明模型在不同数据集上的预测偏差较小,这有助于提高模型的泛化能力。由此可见,PSO优化的BP神经网络模型在本研究中表现出了优异的预测精度和稳定性。
、验证集( ⋅ - 0 . 9 8 0 38)、测试集( R=0 . 9 7 3 8 8 )以及整体数据集( ( R = 0 . 9 6 5 24)上均展现出了较高的相关系数(R值),这表明模型具有很好的拟合能力。图中的拟合线(FT)与理想线( Y = T )非常接近,进一步证实了模型预测值与实际值之间的高度一致性。此外,输出方程中的常数项(0.017至0.014)表明模型在不同数据集上的预测偏差较小,这有助于提高模型的泛化能力。由此可见,PSO优化的BP神经网络模型在本研究中表现出了优异的预测精度和稳定性。
图4展示了模型在迭代过程中的适应度变化情况。可以观察到,适应度值在初始几次迭代中迅速下降,从约0.0442降至0.0430左右,并在随后的迭代中保持稳定。这表明PSO算法能够快速找到较优的参数配置,并在较少的迭代次数内实现收敛。该结果验证了PSO优化策略在提升BP神经网络模型预测精度方面的有效性。
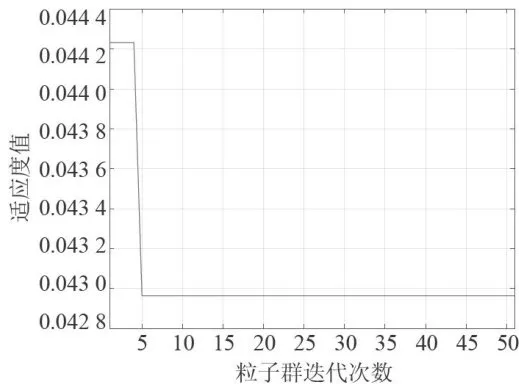 图4粒子群优化模型迭代误差变化曲线
图4粒子群优化模型迭代误差变化曲线图5展示了测试集中预测值与真实值的对比,其中星号代表真实值,圆圈代表预测值。图中的RMSE(均方根误差)为6.3644,这一较低的误差值表明模型具有较高的预测精度。从图中还可以观察到,大多数预测值与真实值紧密对应,尽管在某些样本点上存在一定的偏差。这种偏差可能是由于数据的内在噪声或模型的泛化能力限制所导致的。然而,整体上,预测曲线与真实曲线的趋势保持一致,验证了PSO-BP模型在处理复杂非线性关系时的有效性。
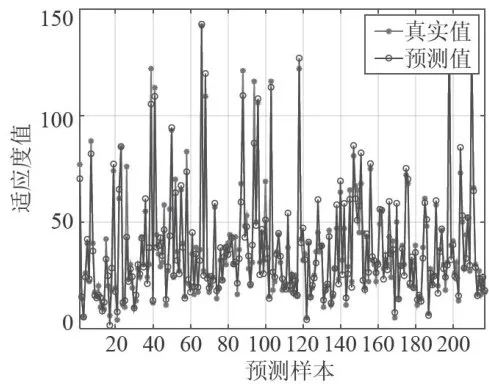 图5测试集预测结果对比
图5测试集预测结果对比图6展示了模型在训练、验证和测试过程中的均方误差(MSE)变化情况。可以观察到,随着训练轮数的增加,MSE迅速下降并趋于稳定,最佳验证性能在第40个Epoch达到0.0010664。这一结果表明,PSO优化的BP神经网络模型能够有效地学习数据特征,并在验证集上实现低误差。图中显示的训练、验证和测试误差曲线接近,说明模型具有良好的泛化能力,未出现明显的过拟合现象。此外,误差曲线的稳定性进一步证实了模型的鲁棒性。总体而言,本研究的模型在测试集上展现了较高的预测精度,为相关领域的预测任务提供了一种有效的解决方案。
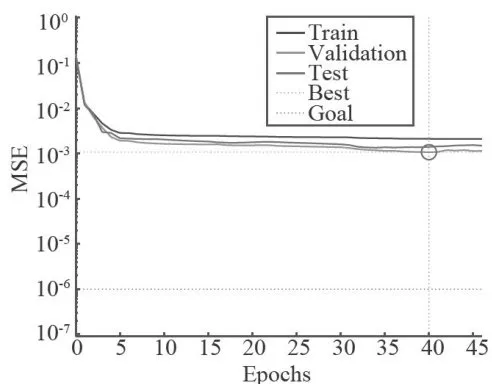 图6均方误差变化曲线
图6均方误差变化曲线4结论
为了准确预测空气中的 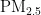 浓度,本文在粒子群优化(PSO)寻优精度和效率的基础上,设计了一种优化的BP神经网络模型,进而构建新的
浓度,本文在粒子群优化(PSO)寻优精度和效率的基础上,设计了一种优化的BP神经网络模型,进而构建新的 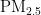 浓度预测模型。具体而言,利用粒子群优化机制对BP神经网络层次间的权值和阈值进行优化,克服其易于陷入局部最优、收敛速度慢的不足。最后,通过配置最优参数的神经网络进行
浓度预测模型。具体而言,利用粒子群优化机制对BP神经网络层次间的权值和阈值进行优化,克服其易于陷入局部最优、收敛速度慢的不足。最后,通过配置最优参数的神经网络进行  浓度预测,有效避免神经网络训练时陷入局部最优,提升预测准确度。选取成都市2021年7月至2024年6月的大气污染物数据作为样本进行实验分析,结果表明,PSO-BP模型不仅收敛速度更快,而且预测精度更高。进一步的研究可以考虑引入莱维飞行和混沌映射,优化PSO粒子群的多样性,从而进一步提升
浓度预测,有效避免神经网络训练时陷入局部最优,提升预测准确度。选取成都市2021年7月至2024年6月的大气污染物数据作为样本进行实验分析,结果表明,PSO-BP模型不仅收敛速度更快,而且预测精度更高。进一步的研究可以考虑引入莱维飞行和混沌映射,优化PSO粒子群的多样性,从而进一步提升 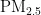 浓度预测的精度。未来的工作可以探索该模型在不同数据集上的表现,并进一步优化算法参数以提升性能。
浓度预测的精度。未来的工作可以探索该模型在不同数据集上的表现,并进一步优化算法参数以提升性能。
参考文献:
[1] ZHOUBH,WANGJ,LIUSX,etal.Extrapolationofan Thropogenic Disturbances on Hazard Elements in 
InatypicalHeavy IndustrialCityinNorthwestChina[J].Environmental Scienceand Pollution Research International,2022,29(43):64582-64596.
[2]吴婷婷.兰州市城区大气 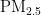 对心血管疾病入院人数的影响及对心肌细胞损伤机制研究[D].兰州:兰州大学,2022.
对心血管疾病入院人数的影响及对心肌细胞损伤机制研究[D].兰州:兰州大学,2022.
[3]YIYANGHU,HAIBINLIAO,LIYUAN,etal.MTLPM:ALong-TermFine-Grained 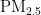 PredictionMethod Based on Spatio-Temporal Graph Neural Network [J].Environmental Monitoring and Assessment,2024,196(12):1240-1240.
PredictionMethod Based on Spatio-Temporal Graph Neural Network [J].Environmental Monitoring and Assessment,2024,196(12):1240-1240.
[4]杨新兴,冯丽华,尉鹏.大气颗粒物 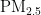 及其危害[J]前沿科学,2012,6(1):22-31.
及其危害[J]前沿科学,2012,6(1):22-31.
[5]刘晓剑,吴永胜,付英斌,等.深圳市空气 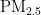 与心脑血管疾病死亡的广义相加模型分析[J].中华疾病控制杂志,2016,20(2):207-209.
与心脑血管疾病死亡的广义相加模型分析[J].中华疾病控制杂志,2016,20(2):207-209.
[6]王媛媛,沈俞,陈秀川,等.基于改进时空因果卷积网络的"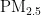 "浓度预测[J].自动化技术与应用,2025,44(2):21-25.
"浓度预测[J].自动化技术与应用,2025,44(2):21-25.
[7]丁成亮,郑洪波.基于改进机器学习的"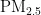 "浓度预测模型研究[J].大连理工大学学报,2024,64(4):353-360.
"浓度预测模型研究[J].大连理工大学学报,2024,64(4):353-360.
[8]林买金,张露露,唐友兵,等.基于CNN-GRU-SSA组合模型的"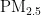 "浓度预测[J].科学技术与工程,2024,24(31):13269-13276.
"浓度预测[J].科学技术与工程,2024,24(31):13269-13276.
[9]张丹宁,吴巧丽,张博.基于BP神经网络的"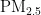 "浓度值预测模型[J].建材技术与应用,2023(2):9-13.
"浓度值预测模型[J].建材技术与应用,2023(2):9-13.
[10]ZHANGSQ,ZHOUHY.BeijingPopulation Migration Analysis Based on WPD-BP Neural Network[C]// ProceedingsVolume 12510, International Conference on Statistics, DataScience,and Computational Intelligence(CSDSCI 2022). Chongqing:SPIE,2023:1-5.
[11]彭豪杰,周杨,胡校飞,等.基于深度学习与随机森林的"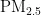 "浓度预测模型[J].遥感学报,2023,27(2):430-440.
"浓度预测模型[J].遥感学报,2023,27(2):430-440.
[12]郑俊褒,华思洁.基于GA-BPNN的"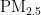 "浓度预测模型[J].软件导刊,2021,20(9):28-32.
"浓度预测模型[J].软件导刊,2021,20(9):28-32.
[13] TIANJW,LIUY,ZHENG WF, et al. SmogPredictionBasedontheDeepBelief-BPNeuralNetworkModel(DBN-BP)[J/OL].UrbanClimate,2022,41:101078[2024-10-20].https://doi.org/10.1016/j.uclim.2021.101078.
[14]KENNEDYJ,EBERHARTR.ParticleSwarmOptimization[C]//ProceedingsofICNN95-InternationalConferenceonNeuralNetworks.Perth,1995,4:1942-1948.
作者简介:李佳林(1987—),男,汉族,四川内江人,讲师,博士在读,研究方向:智能计算和深度学习;侯利明(1987一),男,汉族,河南新乡人,副教授,博士,研究方向:深度学习;张聪(1992一),男,汉族,四川自贡人,工程师,硕士在读,研究方向:机器学习。