陆春华 李 虹 易卓睿
1(交通银行博士后科研工作站,上海 200336) 2(北京大学经济学院,北京 100871)
引 言中国经济进入发展新阶段以来,促进全要素生产率提升被视为实现经济高质量增长的主要着力点[1,2]。党的十九大报告中指出“提高全要素生产率”,党的二十大报告强调“加快建设现代化经济体系,着力提高全要素生产率”。碳交易政策作为一种市场型环境规制手段,在直接促进减排的同时,更高层面的政策目标则是服务我国经济高质量发展[3,4],经济高质量发展的重要体现是全要素生产率提升。目前我国地方碳试点覆盖电力、钢铁、水泥、石化和医药等20 多个高排放、高能耗行业的3000 余家企业,一些行业如石化、电力更是高度关系着国计民生的基础性支柱产业,相关行业和地区的全要素生产率提升对于实现经济高质量发展具有重要意义。那么,碳交易政策是否促进了相关行业和地区的全要素生产率增长呢?在我国经济进入发展新阶段以及碳市场建设加速推进的背景下,对于此问题的研究具有重要意义。
本文关心的另外一个议题则是全要素生产率的变动来源。一般认为,技术进步、技术效率和规模效率是全要素生产率的重要增长来源[5,6]。近年来,许多研究表明我国不同地区、行业在不同时期的全要素生产率增长来源存在较大的差异性,如郑循刚(2010)[7]发现2000 ~2007 年间中国西部农业生产全要素生产率增长的最主要推动力量是技术进步,技术效率和规模效率改进所作的贡献相对有限。牛泽东等(2012)[8]发现1998 ~2009年间中国各地区装备制造业的全要素生产率增长主要来自技术进步,技术效率的贡献相对有限,且规模效率的下降阻碍了全要素生产率增长。那么,如果碳交易试点政策促进了地区工业全要素生产率增长,技术进步、技术效率和规模效率等不同潜在增长因素对全要素生产率增长所作的贡献分别如何? 在不同时间阶段又呈现出怎样的变动特征? 这亦是本文研究的重点。
本文考虑到地区全要素生产率是一个相当宏观的概念,涉及到地区各行各业如农业、工业、服务业等所有的投入产出,在这些行业中,一些行业如农业、服务业并非我国碳交易试点政策所覆盖的行业。当前,我国碳交易试点政策所覆盖的企业大多数是工业企业,为更有针对性的考察碳交易试点政策对其主要覆盖行业的政策效应,本文将以地区的工业行业为研究对象,分析碳交易试点政策是否促进了地区工业全要素生产率的增长以及地区工业全要素生产率的变动来源,对上述问题的讨论有助于厘清我国碳交易试点政策对地区工业全要素生产率的影响效果和实现机制,对于在未来有针对性的完善我国碳市场的政策制度体系,以更好发挥碳交易促进全要素生产率提升、服务经济高质量发展的政策效果具有重要的理论和现实意义。
1 文献综述与本文相关的文献主要有3 类: (1) 关于碳交易政策对技术进步、技术效率和规模效率变动等全要素生产率潜在增长来源的影响; (2) 碳交易政策对全要素生产率的影响; (3) 关于全要素生产率的增长来源分析。
在碳交易政策对技术进步、技术效率和规模效率等全要素生产率潜在增长来源的影响方面,已有文献主要基于实证模型分析了碳交易政策在技术层面的政策效果,但鲜有文献讨论碳交易政策对规模效率的影响。代表性文献如周朝波和覃云(2020)[9]选取2008 ~2016 年间我国30 个省(区、市)数据,基于双重差分法发现我国碳交易试点政策诱发了西部地区的低碳技术进步。王为东等(2020)[10]选取2004 ~2016 年我国282 个城市的面板数据,基于合成控制法发现我国碳交易试点政策诱发了碳试点地区的低碳技术创新活动。曹翔和苏馨儿(2023)[11]选取2009 ~2019 年城市面板数据,基于双重差分法发现我国碳试点政策显着促进了碳试点地区的碳中和技术创新。
在碳交易政策对全要素生产率的影响方面,已有文献主要研究了碳交易政策对地区宏观全要素生产率或绿色全要素生产率的影响,在对宏观全要素生产率的影响层面,如贾智杰等(2023)[12]基于双重差分法发现中国碳交易试点政策在全国层面促进了宏观全要素生产率增长。在对绿色全要素生产率层面,如Feng 等(2021)[13]使用全国及省(区、市)层面的面板数据,基于双重差分法发现我国碳交易试点政策促进了全国绿色全要素生产率的提升。任亚运和傅京燕(2019)[14]、Li 等(2022)[15]和Zhang 等(2021)[16]使用我国省级面板数据,基于双重差分法发现碳交易试点政策促进了碳试点地区绿色全要素生产率提升。总体上,目前以地区工业行业为研究对象的文献较少,且已有文献在讨论了碳交易政策对全要素生产率的影响后,均未对全要素生产率的变动来源进行分析。
在全要素生产率的增长来源分析方面,目前已有一些文献分析了我国不同地区、不同行业在不同时期的全要素生产率增长来源,结论呈现出较大的差异性。已有文献对全要素生产率增长率的分解主要是在两种框架下进行,一种是基于地区或者行业整体的投入产出,使用结合Malmquist指数的DEA 或SFA 方法测算出全要素生产率的变动情况后,基于Malmquist 指数方法进一步分解得到技术效率、技术进步、规模效应等不同因素对全要素生产率变动所起的作用,如袁小慧和范金(2019)[17]发现我国自建国以来,技术效率改善和技术进步提高是推动东、中部地区全要素生产率增长的主要因素,规模效率提升所作的贡献最低。第二种则是基于微观企业数据按一定的加权方式求得加总全要素生产率后,再通过一定方式将加总全要素生产率的变化分解为企业生产率变化、企业间资源配置效率变化等不同部分,如杨汝岱(2015)[18]发现在1998 ~2007 年这10 年间,我国制造业加总全要素生产率增长的约56%贡献来自企业自身生产率提升,企业间资源配置效率提高所作的贡献约为31%,剩余贡献来自于企业的进入和退出。
已有文献表明,我国不同行业或地区在不同时间阶段的全要素生产率增长来源存在相当大的差异性。目前我国碳交易试点覆盖了20 多个高排放、高能耗行业的3000 余家企业,这些企业绝大多数是属于关系国家发展命脉的重要工业部门,在全国碳交易市场已覆盖2200 多家电力企业且在加速建设进程的背景下,厘清碳试点政策冲击下碳试点地区工业全要素生产率的变化情况,并进一步分析清楚其变动来源,对于未来通过完善地方碳试点和加快全国碳市场建设来推进我国工业全要素生产率提升具有重要理论参考价值。
2 研究设计2.1 方法选取与模型构建我国各碳交易试点启动时间并不一致,本文构建多期双重差分模型评估碳交易试点政策对碳试点地区工业全要素生产率增长的影响。具体地,将碳交易试点地区视为处理组,将非碳交易试点地区视为对照组,构建如下多期双重差分模型:
式(1) 中,TFPit为被解释变量,表示地区i在时间t的工业全要素生产率较上一年的增长率。DIDit为多期双重差分变量,用以区分地区i在时间t是否实施了碳交易试点政策。Xit表示与被解释变量相关的一系列控制变量。μi表示地区固定效应,νt表示时间固定效应,εit表示误差项。β是本文关注的核心系数。若β为正值,则表示碳交易政策促进了碳试点地区的工业全要素生产率增长,反之,则表示碳交易政策抑制了碳试点地区工业全要素生产率增长。
2.2 变量选取2.2.1 被解释变量
目前全要素生产率及其增长率的主流测算方法有索洛残差法、隐性分析法,以及将SFA、DEA方法与Malmquist 指数结合的前沿分析法等。由于基于DEA-Malmquist 指数的测算方法具有不需要事先设定生产函数从而避免了因生产函数设置不当带来的误差、通过尽可能利用统计数据信息进行计算从而减少了人的主观意识干扰,以及具有对全要素生产率增长率进一步分解的功能扩展性等优势[19,20],近年来得到了广泛应用。本文亦使用基于DEA-Malmquist 指数的测算方法对工业全要素生产率的增长率进行测算。
(1) DEA-Malmquist 指数方法的基本原理
假设共有w个决策单元(Decision Marketing Units,DMU),每个DMU 在第t期都使用m种投入获取n种产出,其中第i个DMU 在t期的投入向量为,产出向量为,则可根据DEA 方法基本原理[21]构建第t期的生产可能集:
其中,当δ=0 时,St为满足规模收益不变(CRS)的生产可能集; 当δ=1 时,St为满足规模收益可变(VRS)的生产可能集。
DEA-Malmquist 指数方法则是将Malmquist 指数和DEA 理论结合起来,以投入距离函数或产出距离函数为基础定义全要素生产率在不同时期的相对变化[22]。以用产出距离函数为基础定义全要素生产率的增长率为例,t期、t+1 期相邻两期交叉参比Malmquist 指数可表示为:
式(3) 的表达式即为全要素生产率在时间t到时间t+1 期的增长率,其中,分别为地区i在t和t+1 期的投入、产出向量组合。和为产出距离函数,和受到式(2) 中的生产可能集St约束,表示特定时期既定投入向量下产出向量扩张的最大程度,以为例,其表达式为:
(2) 投入产出指标选取
本文采用2003~2022 年我国30 个省(区、市)(基于数据的可获得性,不包括西藏和港、澳、台地区)的工业投入与产出平衡面板数据,使用基于产出导向的相邻两期交叉参比DEA-Malmquist 指数方法计算各地区工业全要素生产率的增长率,测算软件为MAXDEA.9。基于数据的可获得性,本文借鉴李鑫等(2013)[23]、向小东和森健(2018)[24]的做法,采用地区规模以上工业企业代表地区工业行业,具体选用指标如下: ①产出指标: 目前,产出指标一般选取工业总产值[25,26]或者工业增加值[23],本文选取后者,具体使用地区规模以上工业企业的增加值作为产出指标,并根据全国工业品出厂价格指数平减至2000 年水平; ②投入指标: 对于劳动投入,本文参考李鑫等(2014)[23]的做法,采用地区规模以上工业企业年平均用工人数作为投入指标; 对于资本投入,本文参考戴平生(2009)[26]的做法,采用地区规模以上工业固定资产净值年平均余额作为投入指标,并根据历年固定资产投资价格指数进行平减。
2.2.2 核心解释变量
核心解释变量为多期双重差分变量DIDit,用以区分地区i在时间t是否实施了碳交易试点政策。若地区i在时间t实施了碳交易试点政策,则DIDit=1,反之DIDit=0。由于我国7 个地区碳交易市场的启动时间依次为: 2013 年11 月(北京)、2013 年12 月(天津、上海、广东)、2014 年4 月(湖北)、2014 年6 月(重庆)、2016 年12 月(福建),因此DIDit的具体取值规则如下: 当i为北京、天津、上海、广东且t≥2013,或i为重庆、湖北且t≥2014,或i为福建且t≥2016 时,DIDit=1; 除此之外,DIDit=0。
2.2.3 控制变量
本文参考任亚运和傅京燕(2019)[27]、曾诗鸿等(2022)[28]的研究,选取一系列与地方工业经济发展相关的指标作为控制变量。具体包括以下指标: (1) 经济发展水平: 采用地区实际GDP(Rgdp)和人均实际GDP(Prgdp)作为衡量指标,实际GDP 计算基期为2000 年,其中实际GDP 用以反映地区经济发展规模,人均实际GDP 用以反映地区经济发展质量; (2) 城镇化水平: 采用地区城镇化率(Ur)作为衡量指标,计算方式为地区城镇人口数与总人口数之比; (3) 研发投入水平:采用地区研发投入强度(Rd)作为衡量指标,计算方式为地区R&D 经费投入与GDP 之比; (4) 对外开放程度: 采用地区进出口额占GDP 比重(Ie)作为衡量指标; (5) 能源消费水平: 采用地区能源消费总量(Ec)作为衡量指标,能源消费量以标准煤消耗量表示; (6) 能源消费水平: 采用地区的煤炭消耗量占比(Es)作为衡量指标,计算方式为地区煤炭消耗量与能源消耗总量之比; (7) 污染治理投入: 采用地区环境污染治理投资额与GDP 之比(Pa)作为衡量指标; (8) 产业结构: 采用产业高级化程度(Is)作为衡量指标[29],计算方式为地区第三产业增加值与第二产业增加值之比。
具体变量及定义见表1 所示。
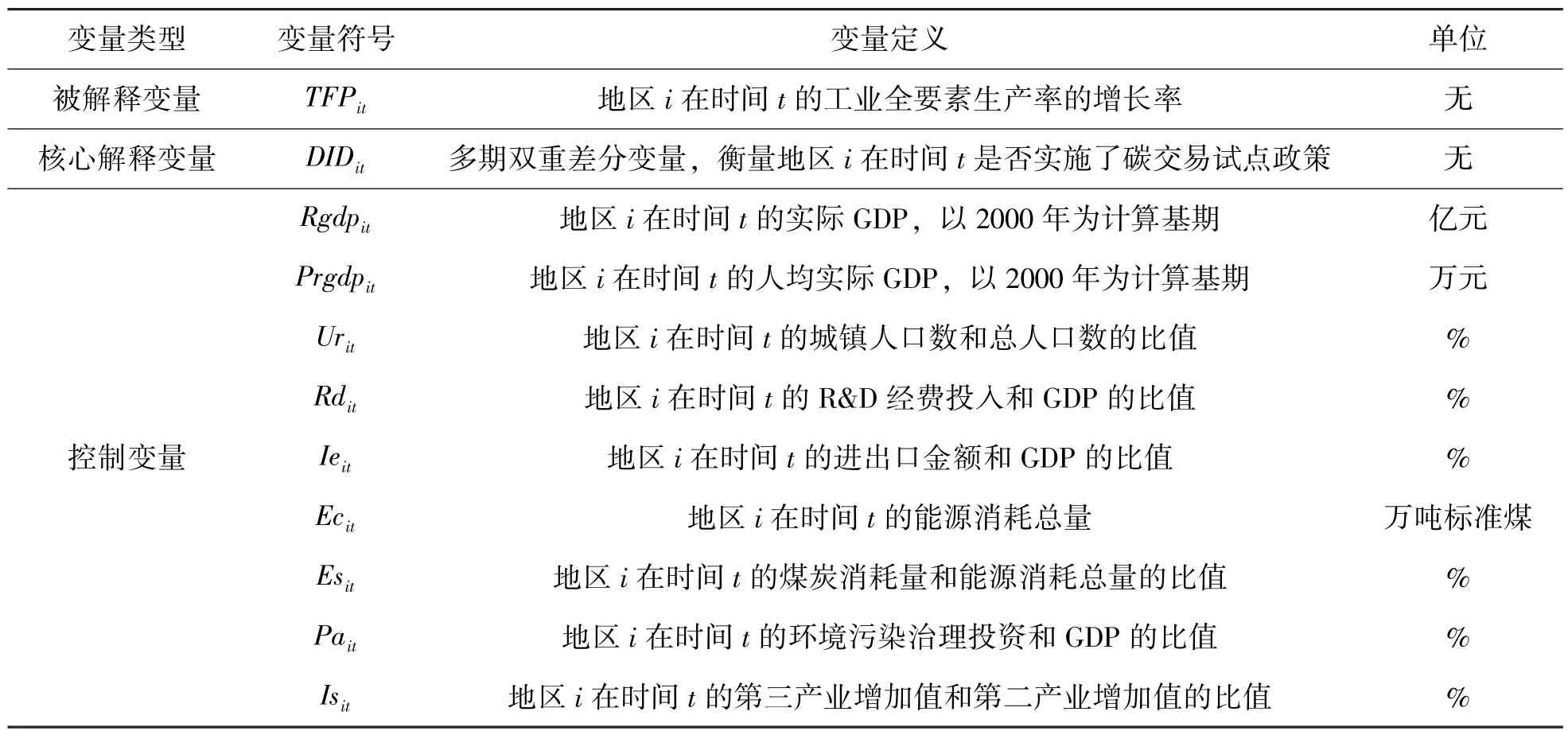
表1 变量选取及定义
2.3 数据来源与说明本文采用2003~2022 年我国30 个省(区、市)(基于数据的可获得性,不包括西藏和港、澳、台地区)的平衡面板数据,数据来自于《中国统计年鉴》、《中国能源统计年鉴》、《中国环境统计年鉴》、《中国科技统计年鉴》 以及各地区统计年鉴和公报。我国先后在北京、上海、天津、重庆、湖北、广东、深圳和福建8 个省(区、市)开展了碳交易试点工作,由于《中国能源统计年鉴》 数据为省级层面,缺少深圳市数据,故本文处理组为北京市、天津市、上海市、重庆市、湖北省、广东省和福建省7 个碳交易政策试点地区(未考虑深圳市),控制组为我国其他省(区、市)。
3 实证结果与分析——碳交易试点政策对地区工业全要素生产率的影响3.1 基准回归结果本文基于式(1) 考察了碳交易试点政策对碳试点地区工业全要素生产率增长率的影响,回归结果见表2,回归(1) 为未添加控制变量的回归结果,回归(2)~(4) 为添加部分控制变量的回归结果,回归(5) 为添加所有控制变量的回归结果,所有回归都控制了地区固定效应和时间固定效应。可以看出,各回归中DID项的回归系数均至少在5%水平上显着为正,表明碳交易试点政策促进了碳试点地区工业全要素生产率增长。
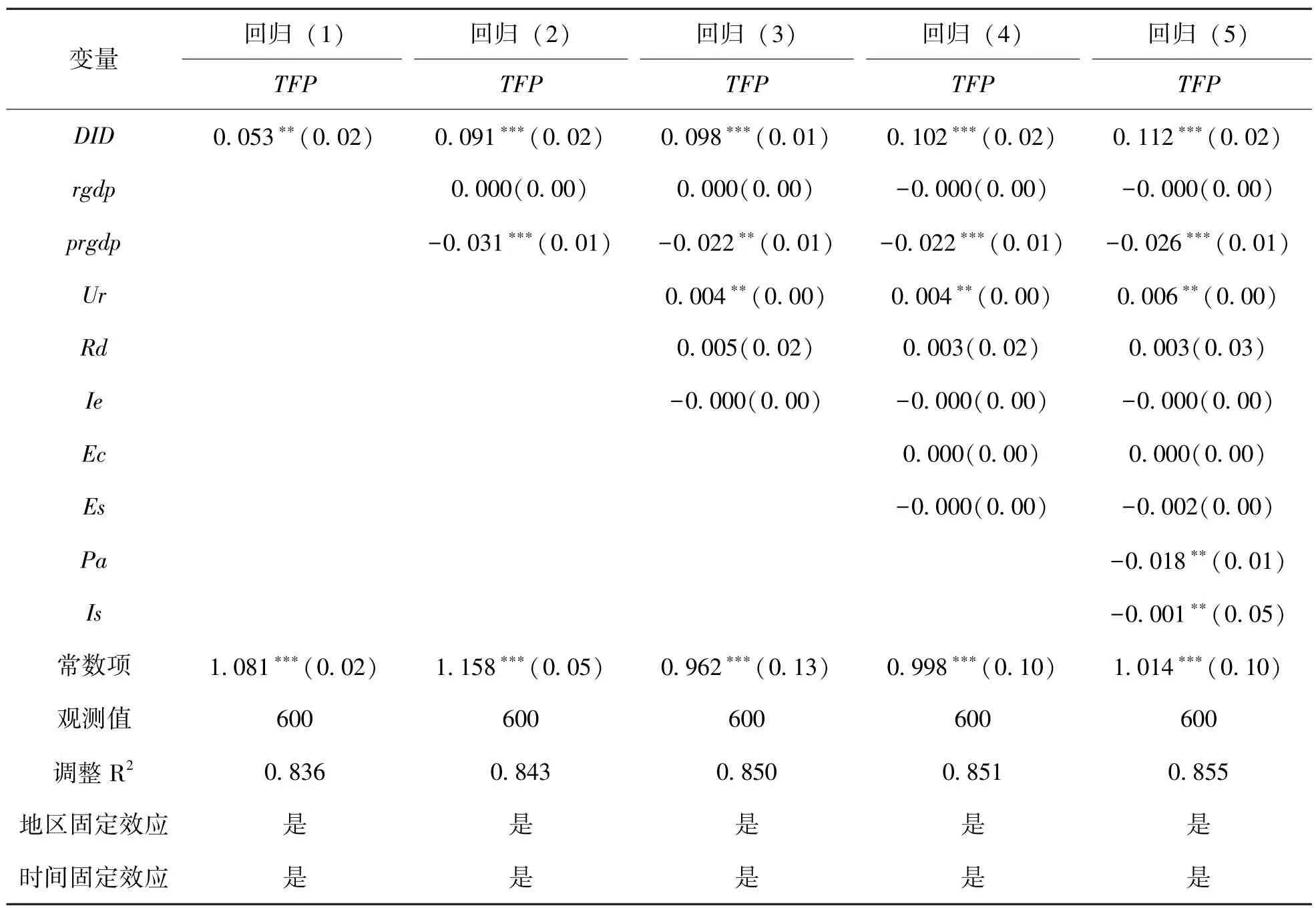
表2 全样本基准回归结果
3.2 稳健性检验①(1) 平行趋势检验
双重差分估计量的一致性需要平行趋势假设成立,即处理组和对照组应在事件发生之前有一致的变动趋势。本文借鉴吴茵茵等(2021)[30]的做法,采用事件研究法来验证平行趋势假设,以碳市场启动之前4 年、启动当年、启动之后4 年的年份虚拟变量与政策虚拟变量的交互项作为自变量来构建模型:
模型(5) 中,DIDipre_s、DIDicurrent、DIDipost_s分别代表碳市场启动之前、启动当年以及启动之后的政策虚拟变量与年份虚拟变量的交互项,βpre_s、βcurrent、βpost_s为对应的系数。由于本文事件研究选取的基准年为政策执行时点的前一年,因此模型(5) 中不存在自变量βpre_1。当βpre_4-βpre_2不显着时,说明处理组地区和对照组地区工业全要素生产率的增长率在碳交易政策执行前的变化趋势相同,模型满足平行趋势假设。
(2) 安慰剂检验
为检验碳试点地区工业全要素生产率的增长率变化主要来源于碳交易试点政策影响,而非由其他不可观测因素导致,本文参考曾诗鸿等(2022)[28]的处理方法进行安慰剂检验,即随机生成碳交易政策执行时间,重复随机抽样1000 次后得到DID项的P 值-系数散点图,观察碳交易政策促进碳试点地区工业全要素生产率提升的政策效应是否依然存在。
(3) PSM-DID 检验
为降低样本选择偏差所造成的内生性问题,本文采用PSM-DID 方法对模型进行稳健性检验。具体思路是: 采用Logit 模型,以政策虚拟变量Policy 为被解释变量,以表1 中的控制变量作为相应的匹配变量,然后采用1 ∶4 近邻匹配的方法进行样本匹配。在进行配对之后,将匹配后的观测值重新进行估计。
(4) 工具变量检验
为解决潜在的内生性问题,本文采取工具变量法进行检验,具体参考Hering 和Poncet (2014)[31]的做法,采用空气流通系数(ACC)作为碳交易政策的工具变量。当空气污染物排放相同时,空气流通系数越低的省(区、市),其污染物监测浓度越大,倾向于采取更为严格的环境规制,其入选碳交易试点的概率越大,满足工具变量相关性假设; 另外,空气流通系数等于风速乘以边界层高度,其大小取决于区域的气象条件和地理环境,与碳排放和环境规制等不存在直接关联,满足工具变量外生性假设。空气流通系数具体数据基于欧洲中级天气预报中心ERA 数据集与中国各省(区、市)经纬度匹配得来。
(5) 样本缩尾截尾检验
为避免变量中因存在极端值而影响回归结果的稳健性,本文对样本分别做了1%分位上的双边缩尾和截尾处理。
(6) 处理效应异质性检验
Goodman-Bacon (2021)[32]指出,多期DID方法存在潜在的异质性处理效应,即同一处理对于不同个体存在差异化效果,这种差异可能表现在接受处理后的时长或者不同时点接受处理的组别两个维度,此时利用传统双向固定效应模型估计量会存在潜在偏误。本文通过Bacon 分解法[32]对处理效应异质性问题进行检验。
4 碳交易试点地区工业全要素生产率增长来源分析前文分析表明,碳交易试点政策促进了碳试点地区工业全要素生产率增长。那么,各潜在增长因素对地区工业全要素生产率增长所作贡献如何? 对此,本文对地区工业全要素生产率的增长率作了进一步的分解以得出结论。
4.1 基于DEA-Malmquist 指数的全要素生产率分解方法DEA-Malmquist 指数方法可以通过进一步的分解来分析技术进步、技术效率、规模效应等不同因素对全要素生产率增长所作的贡献。目前,基于DEA-Malmquist 指数的全要素生产率分解方法主要有4 种,分别是FGLR分解法[33]、FGNZ分解法[25]、RD分解法[34]和ZOFIO分解法[35]。上述4 种方法中,FGLR分解法方法最为基础且未考虑规模效率变化,分解相对粗糙;FGNZ分解法、RD分解法和ZOFIO分解法均考虑规模效率变化,而ZOFIO分解法又包含了FGNZ分解法和RD分解法的所有元素,分解得最为彻底,故本文使用ZIFIO分解法对各碳试点地区的工业全要素生产率增长率进行分解。
ZOFIO分解法下,Malmquist 指数被分解为纯技术进步变化(PTC)、纯技术效率变化(PEC)、规模技术效率变化(SEC)和规模技术进步变化(STC)4 部分,表达式为:
4.2 样本选取由于福建试点启动时间(2016 年)明显晚于其它试点的启动时间(2013 ~2014 年),故本文未将福建试点纳入讨论,仅讨论北京市、天津市、上海市、重庆市、湖北省和广东省6 个试点地区在2013~2022 年的工业全要素生产率变动情况。
4.3 碳交易试点地区工业全要素生产率及其分解指标的总体增长情况本文基于ZIFIO分解法对各碳试点地区历年工业全要素生产率(为方便表述,下文用TFP代表全要素生产率)的增长率进行了分解后,计算了各碳试点地区在2013~2022 年间工业TFP增长率及其分解指标的累积变化(见表3)。
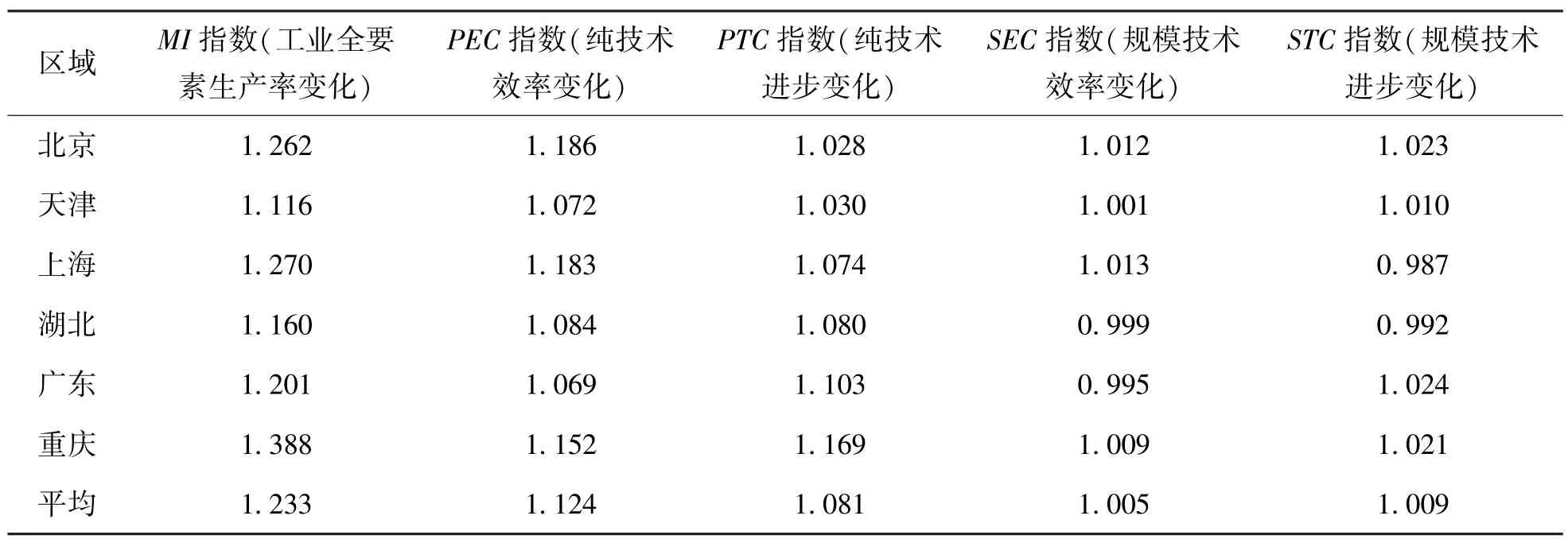
表3 各试点地区工业全要素生产率及其分解指标的累积变化(2013~2022 年)
对于碳试点地区工业TFP的变动,从表3 可以看出,各碳试点地区在2013 ~2022 年间MI指数的平均累积变化为1.233,即各碳试点地区在2013~2022 年工业TFP的平均累积增幅为23.3%。对于各项分解指标的变动,从表3 可以看出,在2013~2022 年间各试点地区纯技术效率水平的平均累积增幅为12.4%,纯技术进步变化水平的平均累积增幅为8.1%,规模效率水平与规模技术水平的平均累积增幅分别为0.5%和0.9%。
上述结果表明,在碳交易政策实施后的2013~2022 年间,各碳试点地区的工业TFP平均实现了23.3%的累计增幅,在各分解指标中,纯技术效率水平的增长情况优于其他分解指标,表明纯技术效率水平提升对碳试点地区工业TFP增长的贡献最高。
4.4 各分解指标对碳交易试点地区工业全要素生产率的增长贡献及变化趋势上文分析结果初步表明,在2013 ~2022 年整个样本期内,纯技术效率水平提升对碳试点地区工业TFP增长的贡献最高。那么,各分解项所作的贡献具体占比以及动态变化趋势如何? 为探究上述问题,有必要以更为量化的方式计算各分解指标对地区工业TFP增长的贡献度。
(1) 贡献度计算方法
根据式(6),ZOFIO分解法将代表全要素生产率变化率的MI指数分解成了PEC指数、PTC指数、SEC指数和STC指数4 个因子的乘积。当一个数是若干因子的乘积时,可以基于乘积因子分解法计算出各因子对乘积的增长贡献,代表性方法有拉氏指数分解法、迪氏指数分解法等,其中对数平均迪氏指数分解法(LMDI分解法)由于具有完全分解和结果唯一性等优势,成为近年来最为流行的分解方法之一[36]。LMDI分解方法的核心表达式如下[37]:
假设在时期t,整体指标V可表达为k个因子指标的乘积:
以RATIOV表示整体指标V在时期t到时期t+n的增长率:
那么在时期t到时期t+n,整体指标V的增长率RATIOV可以分解到每个因子指标上:
式(13) 中,加权系数WEIGHTi即第i个因子指标的贡献比例,具体取第i个因子Xi变化比值的自然对数除以整体指标V变化比值的自然对数,表达式为:
(2) 各分解指标对碳试点地区工业全要素生产率增长贡献
本文基于表3 的结果,使用LMDI分解法测算了2013~2022 年间各分解指标对碳试点地区工业TFP增长的累积贡献,计算结果见表4。可以看出,在碳交易试点政策启动后的2013 ~2022 年间的整个样本期内,技术进步、技术效率以及规模效率提升均对碳试点地区工业TFP增长作出了积极的贡献,但从贡献的比例来看,试点地区工业TFP增长的主要来源是纯技术效率提升和纯技术进步水平提升,其中纯技术效率对各碳试点地区工业TFP增长的平均贡献为56.8%,纯技术进步所作的平均贡献为36.9%,二者合计贡献为93.7%。规模效率变化所作出的增长贡献则相对有限,其中规模技术效率所作的平均贡献为1.8%,规模技术进步所作的平均贡献为4.5%,二者合计贡献为6.3%。
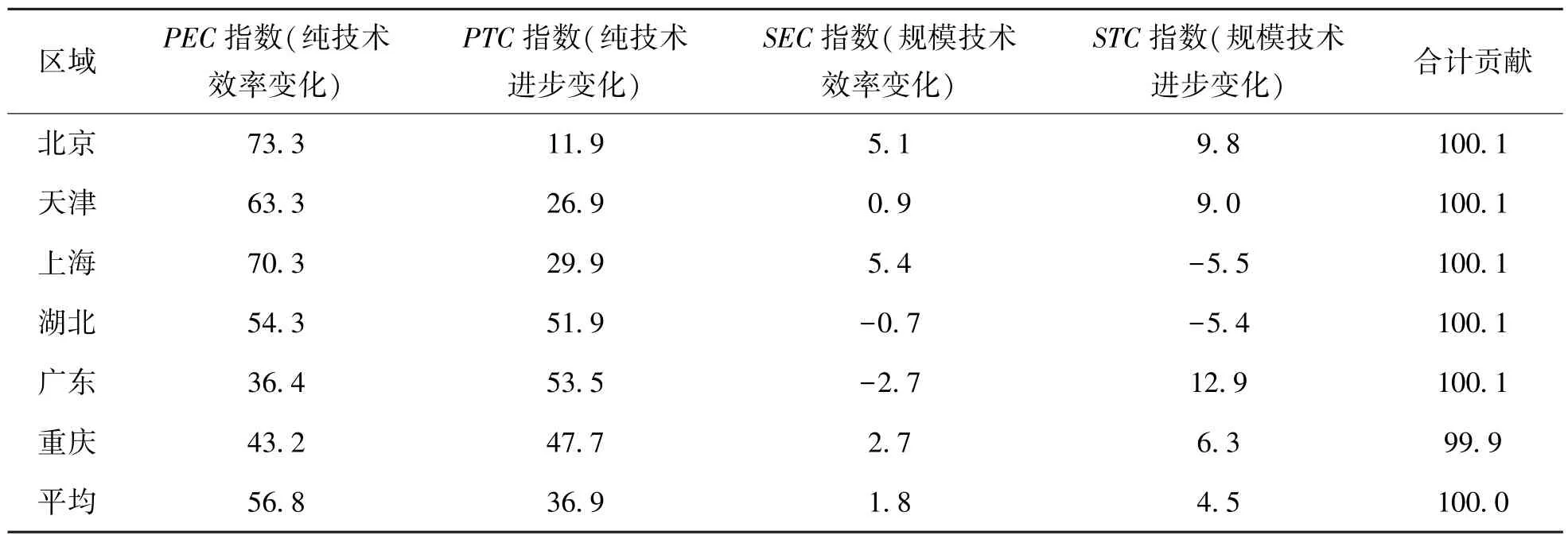
表4 分解指标对试点地区工业全要素生产率增长的累积贡献率(2013~2022 年)单位:%
为进一步分析各分解指标对碳试点地区工业TFP增长所作贡献的动态变化,本文按照测算表4 中2013~2022 年平均贡献率的方法,测算了不同样本期内分解指标对碳试点地区工业TFP增长的平均累积贡献率,具体结果见表5。可以看出随着样本区间的不断缩短,呈现的总体规律是规模效率指标(SEC指数与STC指数)所贡献的权重越来越大,纯技术进步变化所贡献的权重越来越小,纯技术效率变化具体的所贡献的权重则稳定在40%~60%之间。以上结果反映出近年来碳试点地区工业TFP的增长仍然主要依赖纯技术效率水平的提升,但是从动态变化上看,纯技术进步所作的贡献呈下降趋势,规模效率变化所作的贡献呈增加趋势,在2019~2022 年、2020~2022 年以及2021~2022 年3 个样本期内,规模效率(SEC指数与STC指数)提升所作的平均贡献均超过了20%。

表5 分解指标在不同时期内对试点地区工业全要素生产率增长的平均累积贡献率单位:%
4.5 指标变化解读本文的研究结果表明,在碳交易试点政策启动后的2013~2022 年间的整个样本期内,各碳试点地区的工业全要素生产率平均实现了23.3%的累计增幅,且增长主要来源于纯技术进步和纯技术效率提升,规模效率提升的贡献相对较低。具体的,在2013~2022 年间,纯技术效率、纯技术进步和规模效率所作的平均贡献分别为56.8%、36.9%和6.3%。但是近年来,纯技术进步发挥的作用呈下降趋势,规模效率提升所发挥的作用在稳步提升,在2019~2022 年、2020 ~2022 年以及2021 ~2022 年3 个样本期内,规模效率提升所作的平均贡献均超过了20%。
回到各分解指标定义,纯技术进步水平反映了在既定的要素投入水平下,最优生产前沿面整体向外移动的能力,纯技术进步水平提升意味着社会潜在最大产能的提升。纯技术效率水平体现的是生产部门在既定技术水平下,在给定要素投入条件下实现最大产出,或者在给定产出水平下实现最小要素投入的能力,主要反映了要素资源在生产部门内的利用效率,体现了社会潜在最大产能实际得以释放的能力。本文研究结果表明,在2013~2022 年整个样本期内,碳试点地区工业全要素生产率的增长主要依赖于纯技术水平进步和纯技术效率水平提升,即在样本期内,纯技术水平进步提升了碳试点地区的潜在最大工业产能;另外,纯技术效率水平提升促进了碳试点地区的潜在最大工业产能的释放,二者共同促进了碳试点地区工业全要素生产率的提升。
规模效率反映的则是生产部门实际规模与最优生产规模的差距,即生产部门多大程度在最优规模上组织生产,体现的是不同生产部门根据自身生产效率调整生产规模的能力,亦是资源在不同生产部门间配置效率的重要体现。本文研究结果表明,在2013~2022 年整个样本期内,从变化趋势来看,近年来碳试点地区依赖于纯技术效率提升和纯技术进步实现工业全要素生产率增长的空间在不断缩小,亟待依托规模效率改善的新的增长模式,即将更多的资源配置到生产率更高的生产部门,缩小高效率生产部门实际生产规模与最优生产规模的差距。
5 研究结论与政策建议本文基于DEA-Malmquist 指数方法测算了我国各省(区、市)2003 ~2022 年的工业全要素生产率,基于多期双重差分法研究发现碳交易试点政策有助于促进碳试点地区工业全要素生产率增长。本文同时基于DEA-Malmquist 指数方法分析了碳试点地区工业全要素生产率的增长来源,发现在2013~2022 年间,碳试点地区工业全要素生产率的增长主要来源于纯技术进步和纯技术效率提升,规模效率提升的贡献相对较低。但是从变化趋势来看,近年来碳试点地区依赖于纯技术效率提升和纯技术进步实现工业全要素生产率增长的空间在不断缩小,规模效率提升所发挥的作用在稳步增强,未来碳试点地区工业全要素生产率增长将愈发依托规模效率改善的增长模式。
基于本文研究结论有以下思考和建议: (1)本文的研究表明碳交易政策可显着促进碳试点地区的工业全要素生产率提升,因此建议继续扩大被纳入地方碳试点的企业范围,并做好和全国碳市场的衔接,尤其是目前全国碳市场仅覆盖电力行业,有必要进一步丰富全国碳市场的交易主体和交易品种,逐步纳入石化、有色、钢铁等高排放行业的企业; (2) 本文的研究表明近年来纯技术进步和纯技术效率提升对碳试点地区工业全要素生产率增长的贡献呈下降趋势,而能反映资源配置效率改善的规模效率提升所发挥的作用在稳步增强,未来地区工业全要素生产率增长将愈发依托规模效率改善的增长模式,因此建议在碳交易政策实施过程中,不断完善能影响资源配置效率的碳价制定和碳配额分配等机制,让各减排主体能更好的依据碳价这一价格信号确定碳排放要素资源在生产中的配置,以进一步发挥碳交易政策改善资源配置效率的政策效果,更好促进全要素生产率提升和服务经济高质量发展。
注释:
①限于本文篇幅,稳健性检验的具体计算结果留存备索。