陈青兰林冠华魏秋建
1(厦门理工学院,厦门 361024)2(台湾南亚科技公司,台湾 33383)3(台湾中华大学,台湾 30012)
项目组合选择研究 :基于模糊理论的模型建构及验证
陈青兰1林冠华2魏秋建3
1(厦门理工学院,厦门 361024)2(台湾南亚科技公司,台湾 33383)3(台湾中华大学,台湾 30012)
项目组合的选定与企业经营息息相关,然而传统的选择方法存在许多限制。本文应用模糊理论建构一个项目组合的决策模型,模型中纳入了成本、利润及风险等3个决策因子,探讨在资源有限的情况下项目成本及获利的交互影响关系 ,并利用模糊归属函数建构一个数学规划模型。为了验证模型的有效性,用此模型与传统模型进行求解比较,证实了所提出模型的实用性。
项目组合选择 交互影响 模糊归属函数 模糊理论
引 言如何在资源有限条件下选择适当的项目组合,实现绩效最大化,是每个组织的重要目标[1]。项目组合选择及绩效的相关研究经历了从单一标准到多标准,从较少考虑资源限制到纳入资源限制考量的发展历程。项目的选择最初只考虑单一目标 ,以成本/效益方法作为评估标准[2]。其后的研究提出了打分 (Scoring)方法[3,4]和优先级 (Ranking)方法[5],二者均考虑到项目组合时需同时纳入成本、利润、风险等多重衡量标准,以打分或者评级方法提升项目组合绩效。随着竞争加剧,学术界意识到资源的稀缺性成为竞争的瓶颈,此后研究开始将资源上限问题纳入重点考量[6,7]。然而,尽管相关文献已经考虑了多目标和资源稀缺性,以上项目组合选择的研究均未考虑拟组合项目之间的交互作用。学者指出,项目之间存在交互影响[8]。企业在同时间内所进行的项目不只一个,所以应考虑如何将有限的资源有效地分配给什么样的项目组合,因此后续研究提出权重配置的项目组合选择模型[9],但其缺点是权重配置本身存在主观性。为此近期的研究开始以模糊 (FUZZY)理论建构决策模型,旨在以模糊理论解决权重的主观性问题[10-14]。
纵观以上相关研究,虽然当前文献已经提供了一些项目组合选择的决策模型,然而这些方法仍有前述的许多限制,如,忽视了资源稀缺性,项目间相互关系的线性假设也广为诟病,无法将相关项目选择标准合并为单一目标,即便后期的多目标模型也往往忽略软件及硬件资源在多项目中的分享,而权重配置更是决策的重点。现有研究已经从不同角度力图突破上述限制,但是,在全面考虑这些假设的基础上建构一个较为完整条件下的项目组合选择决策模型,这类研究当前还较少见。本研究探讨在资源限制下,同时有多项目进行且项目彼此存在交互影响时,组织该如何进行项目组合的选定 ,为了解决权重配置的主观性问题,本文利用FUZZY理论建构项目组合选择模型,目标如下:考虑项目间的交互影响 ,为项目的组合构建一个多目标数学模型,并利用FUZZY理论对模型进行简化,将项目选择的多标准合并为单一目标,最后比较及验证传统线性模型与FUZZY理论数学模型所选择的项目组合绩效。
1 问题定义本模型目标函数包含:利润最大化;风险最小化;成本最小化。
1.1 利润函数
利润为完成项目所获得的利润。研究假设,执行两个或两个以上相关项目所获得的利润会超过它们个别执行所获得的利润。即Pij>Pi+Pj,Pijk>Pi+Pj+Pk,依此类推。利润函数如式 (1),其中ZP代表利润的目标函数,Pi、Pij分别指 “单独执行项目i”和 “同时执行项目i和j”可能产生的利润值,Pijk表示同时执行项目i、j及k所产生的利润。
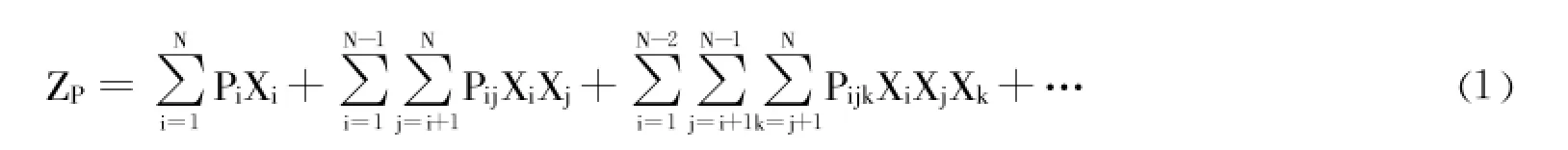

1.2 成本函数
项目成本是完成项目所需要投入的成本。研究将成本划分为硬件成本、软件成本、其他成本[10],其他成本包含了开发成本,如计算机测试成本等。成本函数如式 (2),其中ZC代表成本的目标函数,Ci指执行项目i可能需要承担的成本,Cij表示资源被项目i和项目j共享所需程度的成本。以此类推。
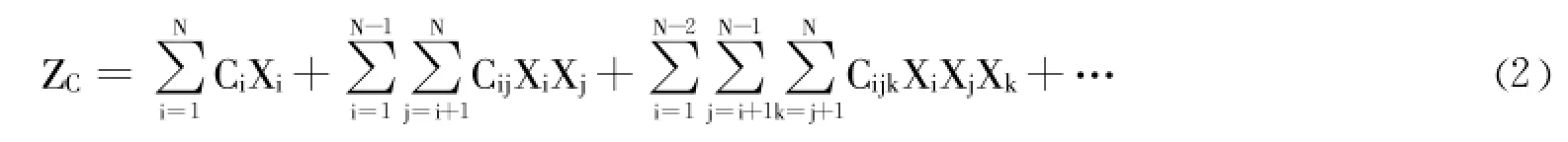
1.3 风险函数
研究为每一个项目进行风险评分,评分以项目的科技环境、项目大小以及先前相似项目的经验为依据。项目风险分数介于0~15分,分数愈高表示组合中所需承担的项目风险也愈高。风险函数如式 (3),其中ZR代表成本的目标函数,Ri指执行项目i可能发生的风险值,Rij表示当同时执行项目i和项目j可能产生的风险值,以此类推。
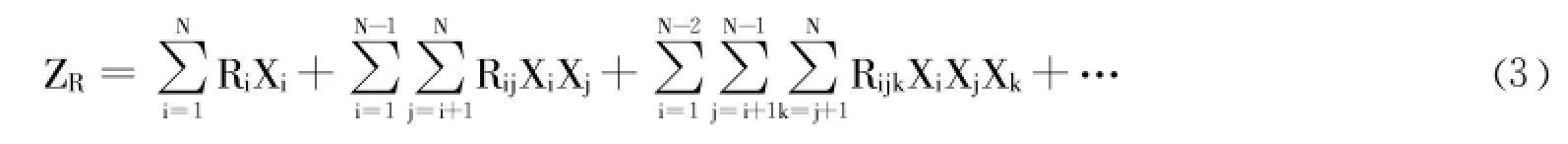
1.4 项目间关系
项目彼此间的关系式如方程 (4)。
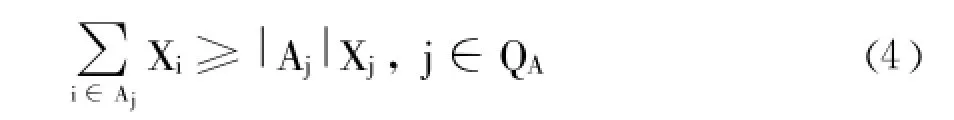
其中,X代表项目,Xi与Xj分别代表项目i和项目j,而Aj为所有项目的集合,QA为被选中要执行的项目的子集合。
2 基于FUZZY理论的数学模型1965年,为将人类的主观判断中的不确定性予以量化,加州大学Zaden教授提出了FUZZY集合。尔后,在多位研究者的努力下于1970年开始了FUZZY理论。1980年,丹麦Smidth公司开发了FUZZY控制器,自此 FUZZY走向了实用路线。FUZZY理论主要用以处理涉及面大且复杂的决策问题,在做决策时,模型可判断所涉及的所有信息,并组合这些信息以获得各种为达成目标的组合方案。其目标式以组合方案的目标达到程度来表示,因此决策的最优解会出现在所有的归属函数及限制式的交点。本研究根据FUZZY理论,利用归属函数做出下列的定义。
元素X所有集合中,FUZZY子集合M其定义为:
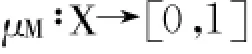
此为归属函数μM(X)表示X于M的归属度。若μM(X)的值愈趋近于1,表示X于M的归属度愈大。反之亦然,若μM(X)的值愈趋近于0,表示X于M的归属度愈小。
2.1 寻找上下界
针对每一项目标方程式寻找其上界 (UK)及下界 (LK),即,当目标函数的得分低于下界时,则目标函数及其归属程度为0;当目标函数的得分低于下界时,则目标函数其归属程度为1。本研究目标式的上界为UC,UR,UP;下界为LC,LR,LP,分别代表了成本 (Cost)、风险 (Risk)、利润(Profits)的上下界值。
2.2 定义各目标式的归属函数关系式
2.2.1 利润
利润代表所执行的项目所获利润的总数,企业目标是获取更高的利润,故利润的归属函数图为非递减函数。见图1。
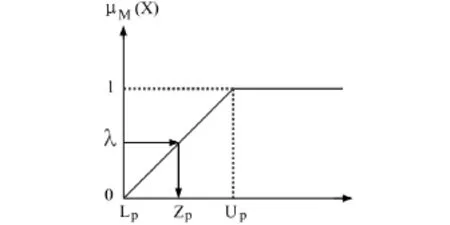
图1 项目利润归属函数
由图1中两个相似三角形的比例关系 ,可以求得当ZP介于LP与UP之间时其λ值如公式 (5):
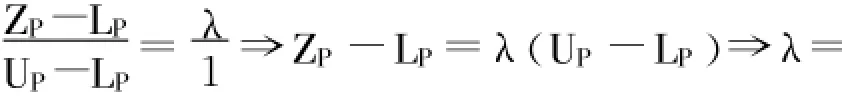

而利润归属函数式如方程式 (6)所示:
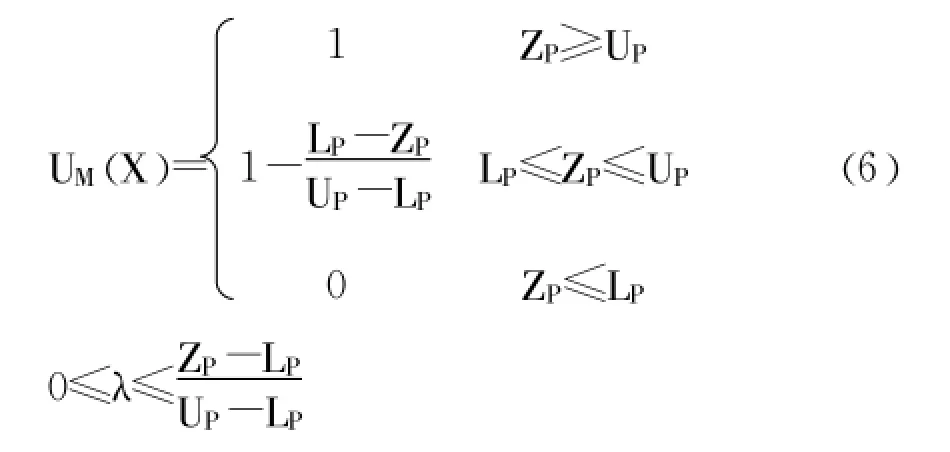
2.2.2 成本
成本为执行项目所需要的费用,其中包含了软件、硬件费用以及其他费用,成本越小越好,为非递增函数。见图2。
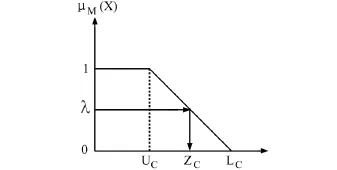
图2 项目成本归属函数
由图2中两个相似三角形的比例关系 ,可以求得当ZC介于LC与UC之间时其λ值如公式 (7):
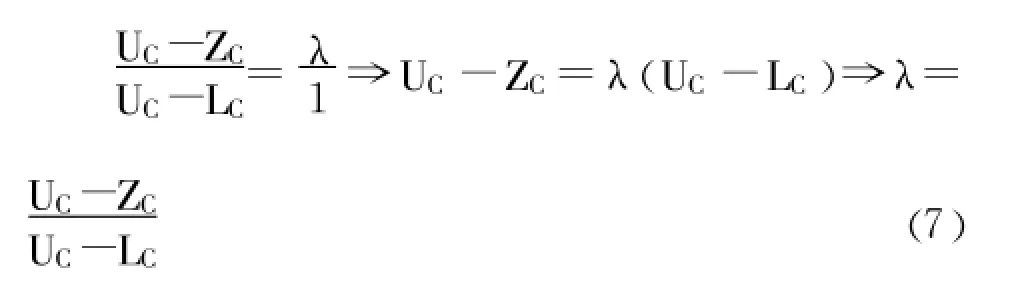
而成本归属函数式如方程 (8)所示。
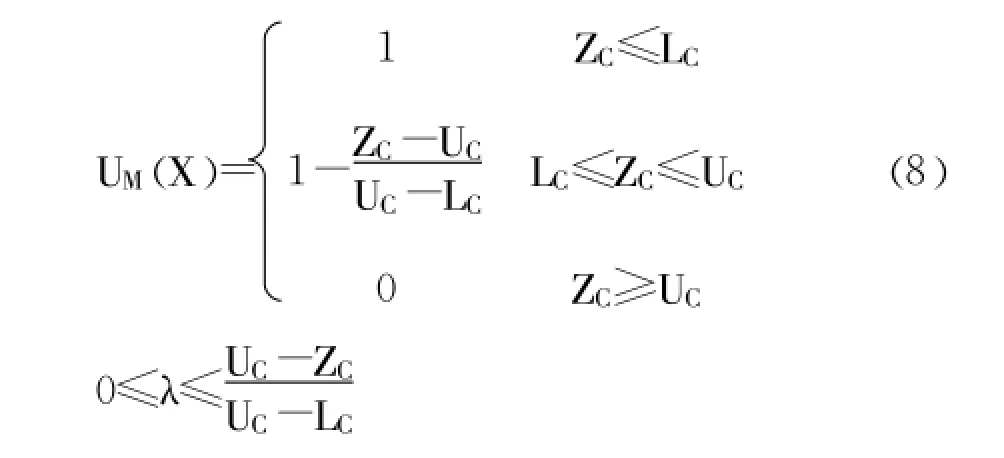
2.2.3 风险
风险代表所执行的项目所获风险的总数,企业所承担的风险越小越好,故风险的归属函数图为非递增函数。见图 (3)。
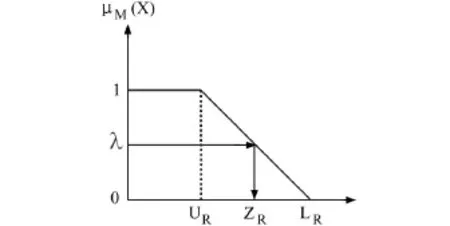
图3 项目风险归属函数
由图3中两个相似三角形的比例关系 ,可以求得当ZR介于LR与UR之间时其λ值如公式 (9):
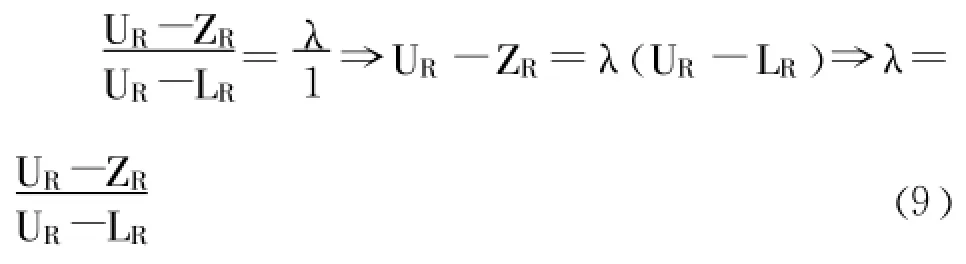
而风险归属函数式如方程 (10)所示。
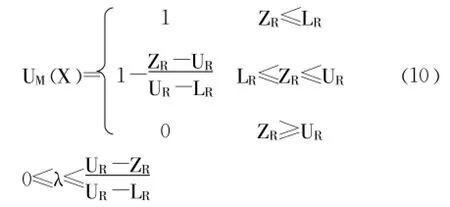
2.3 构建FUZZY线性模型
最后将上述的3个目标式,利用FUZZY理论组合成一个目标式如方程式 (11)所示 (同时考虑项目成本含硬件、软件、其他成本)。
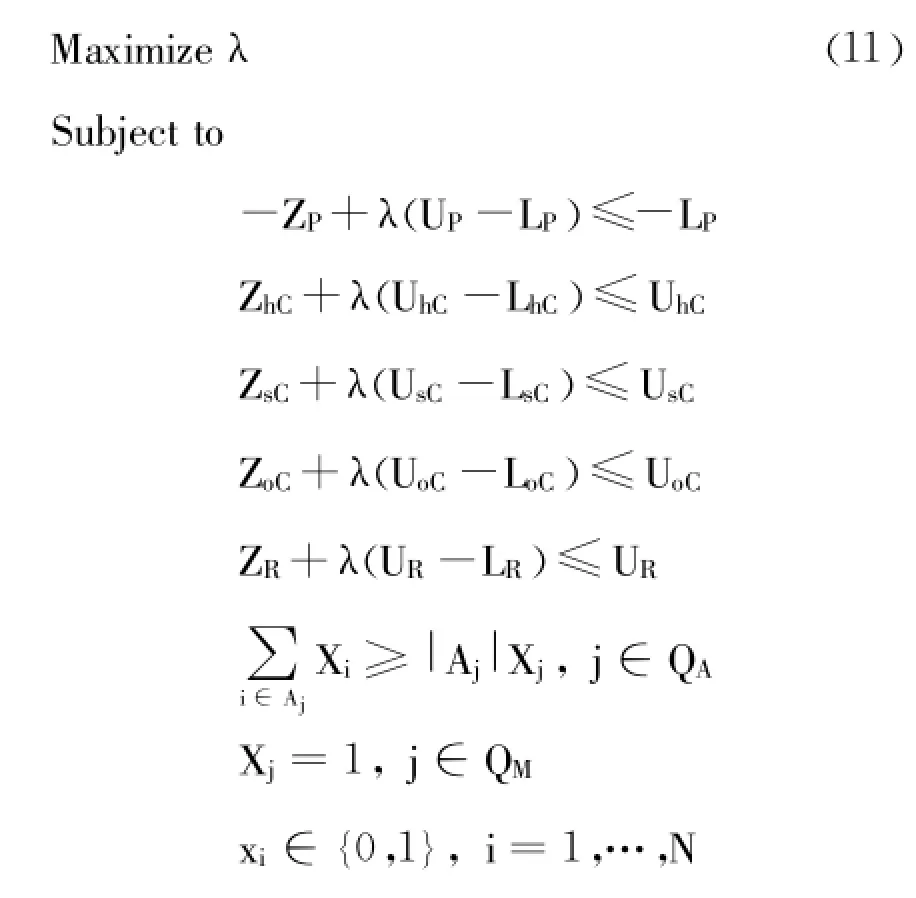
其中,ZhC,ZsC,ZoC分别表示执行项目的硬件成本、软件成本和其他成本。
3 FUZZY模型与传统线性模型之比较为了验证本模型的有效性,我们引用文献[9]中的一个实例进行测试,并将结果与文献[9]中利用传统模式计算出的结果进行比较。篇幅所限,该文献中计算的过程不再赘述,仅以最后结果做比较。
利用本研究所提出的模型来对这个实例求解,其中 ,ZP,ZhC,ZsC,ZoC,ZR的数值如表1所示。
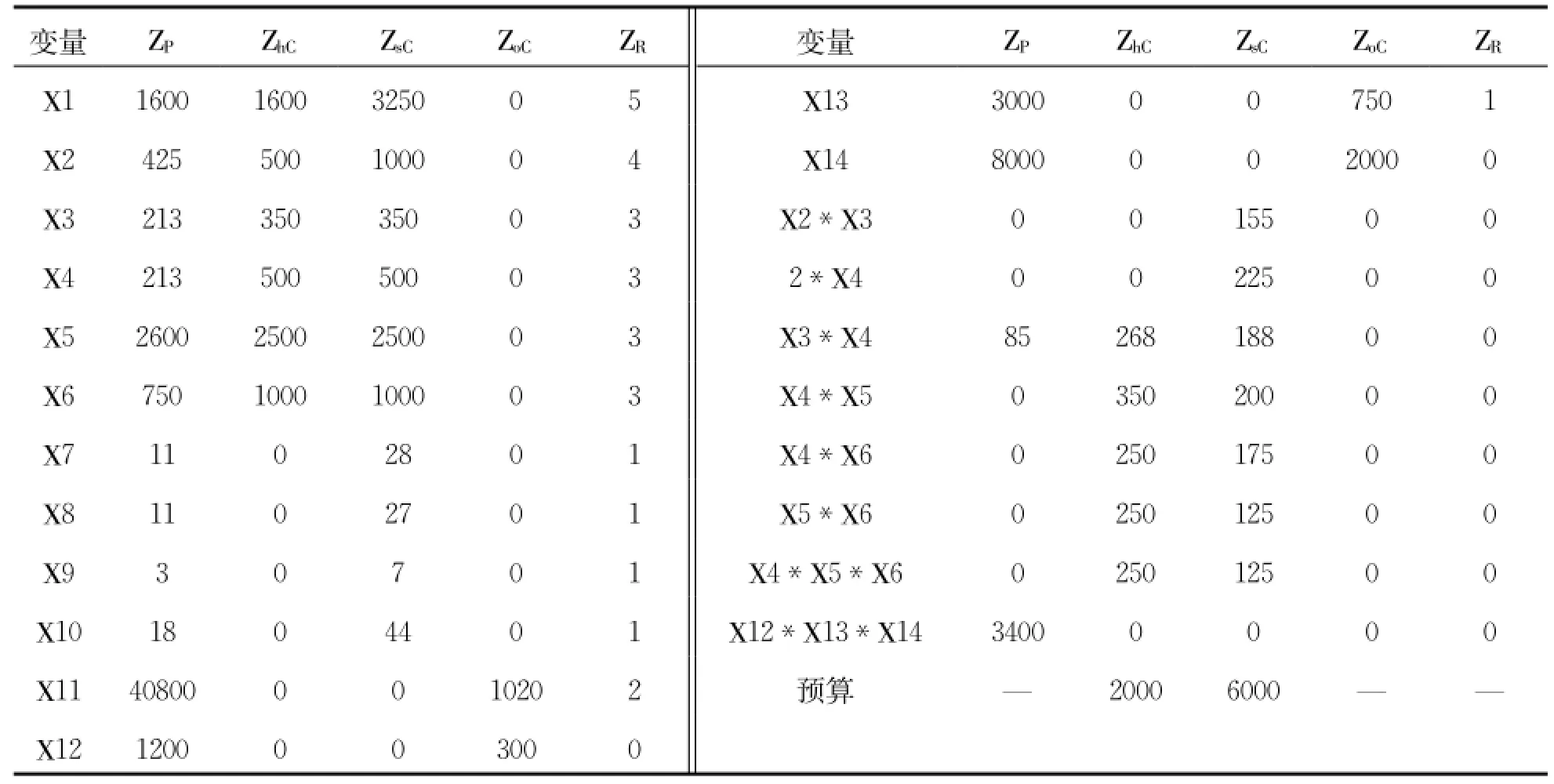
表1 本研究模型基本资料千元
最后利用LINGO软件执行上述的FUZZY非线性规划模型。为了比较本模型与传统线性模型的差别,表2将二者所选出的项目的组合绩效进行比较。从表2中P/ZoC一列所表达的项目组合绩效来看,灰色底纹所在行的FUZZY方法所选出的项目组合效益,优于或者等同于文献[9]所提线性模型结果的效益,其中有5组的组合绩效明显更优,表明本研究所提的FUZZY模型为更优决策方式。
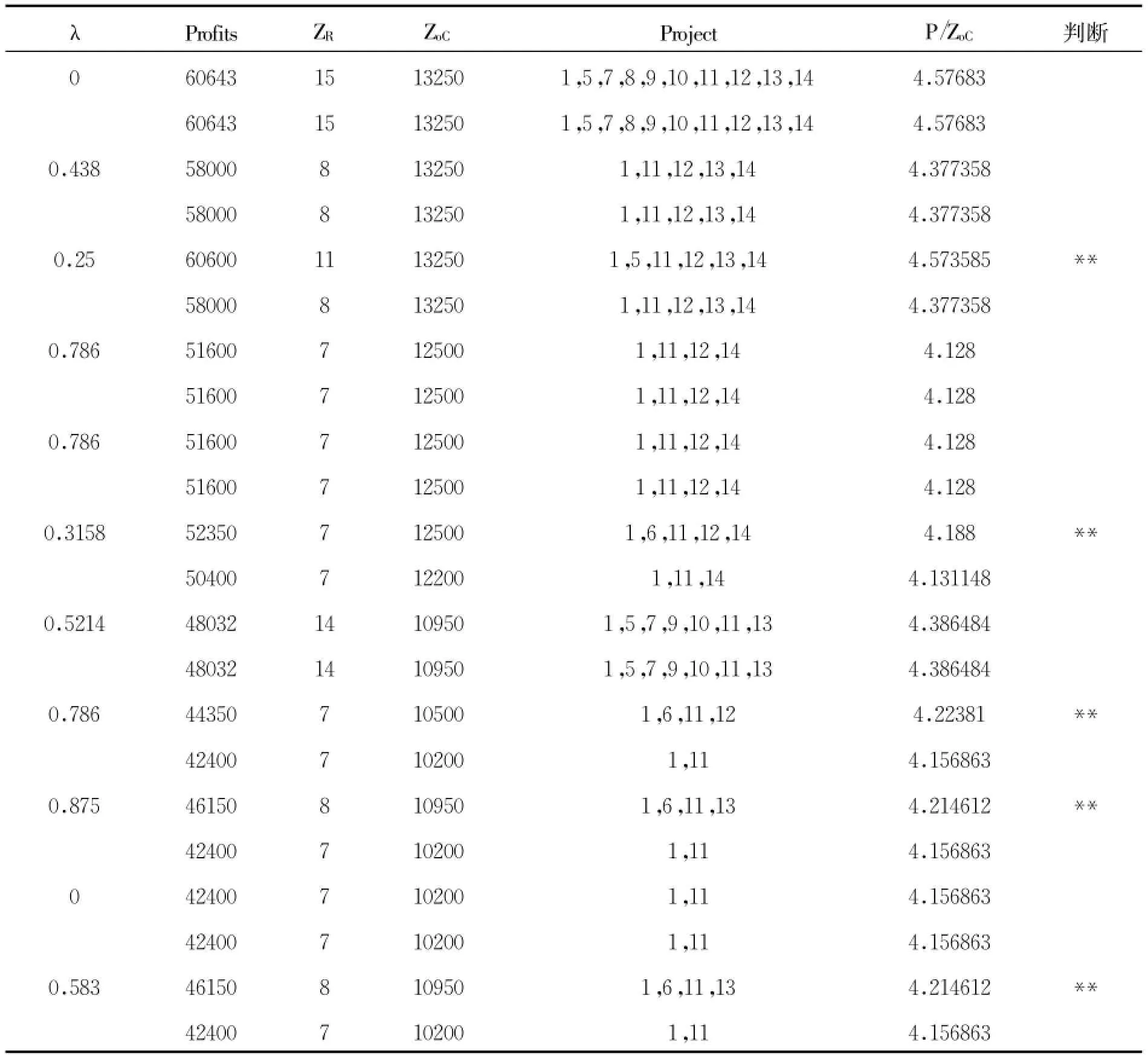
表2 本研究模型与传统模型的项目组合绩效比较
4 结 语本研究利用FUZZY理论建构多目标方程式,以便企业进行多目标下的项目组合选择。为了评估我们所建构的FUZZY模型与传统线性模型所得到的项目组合,研究以利润/其他成本(P/ZoC)作为评估的准则,运行结果表明,我们利用FUZZY理论建构的模型所选出的项目组合的绩效均大于或等于传统线性模型所选出的项目组合。研究为企业的项目组合选择提供了一种可行的思路。
[1]杨颖 ,刘娟娟 ,李兴国.创新项目组合管理绩效关键影响因素的实证研究[J].工业技术经济,2016,35(2):9~17
[2]KING,John Leslie;SCHREMS,Edward L.Cost-benefit Analysis in Information Systems Development and Operation[J].ACM Computing Sur-veys(CSUR),1978,10(1):19~34
[3]LUCAS,Henry C.;MOORE,John R.A Multiple-criterion Scoring Approach to Information System Project Selection[M].New York University,Graduate School of Business Administration,1976
[4]MELONE,N.P.;WHARTON,T.J..Strategies for MIS Project Selection [J].Journal of Systems Management,1984,35(2):26~33
[5]BUSS,M.D..How to Rank Computer Projects[J].Harvard Business review,1982,61(1):118~125
[6]SCHNIEDERJANS,Marc J.;SANTHANAM,Radhika.A Multi-objective Constrained Resource Information System Project Selection Method [J].European Journal of Operational Research,1993,70(2):244~253
[7]SANTHANAM,R.;MURALIDHAR,K.;SCHNIEDERJANS,M.A Zero-one Goal Programming Approach for Information System Project Selection[J].Omega,1989,17(6):583~593
[8]AAKER,David A.;TYEBJEE,Tyzoon T.A Model for the Selection of Interdependent R&D Projects[J].Engineering Management,IEEE Transactions on,1978,(2):30~36
[9]SANTHANAM,Radhika;KYPARISIS,Jerzy.A Multiple Criteria Decision Model for Information System Project Selection[J].Computers& Operations Research,1995,22(8):807~818
[10]张树山,郭坤 ,孙毅.全球供应链系统环境下科技协同创新伙伴关系模糊组合评估方法[J].中国软科学 ,2014,(5):164~172
[11]CHANG,Ping-Teng;LEE,Jung-Hua.A FUZZY DEA and Knapsack Formulation Integrated Model for Project Selection[J].Computers &Operations Research,2012,39(1):112~125
[12]KHALILI-DAMGHANI,Kaveh;SADI-NEZHAD,Soheil;TAVANA,Madjid.Solving Multi-period Project Selection Problems with FUZZY Goal Programming Based on TOPSIS and a FUZZY Preference Relation [J].Information Sciences,2013,252:42~61
[13]TAN,Yong-tao,et al.Construction Project Selection Using FUZZY TOPSIS Approach[J].Journal of Modelling in Management,2010,5 (3):302~315
[14]AMIRI,Morteza Pakdin.Project Selection for Oil-fields Development By Using the AHP and FUZZY TOPSIS Methods[J].Expert Systems with Applications,2010,37(9):6218~6224
Portfolio Selection:Model Construction and Verification Based on Fuzzy Theory
Chen Qinglan1Lin Guanhua2Wei Qiujian3(1.Xiamen University of Technology,Xiamen 361024,China;2.Nanya Technology Corporation,Taiwan 33383,China;3.Chung Hua University,Taiwan 30012,China)
Portfolio selection is vital to the enterprises,however,there are many limitations of traditional portfolio selection methods.Therefore,a decision model to select portfolio based on fuzzy theory is build in this research,with key decision factors,costs,profits and risks involved.This paper builds a mathematical programming model with fuzzy membership function in the context of limited resources,considering the interactions effect of costs and profits among projects.In order to verify the validity of the model,comparison between the proposed model and the traditional model is launched,which confirms the applicability of the proposed model.
portfolio selection;interaction;fuzzy membership function;fuzzy theory
(责任编辑:王 平)
10.3969/j.issn.1004-910X.2016.08.008
F224
A
2016—04—02
国家自然科学基金项目 “倒向协同创新项目治理网络研究”(项目编号 :71572094)。
陈青兰 ,厦门理工学院经济与管理学院副教授 ,管理学博士。研究方向 :项目管理、战略管理。林冠华 ,台湾南亚科技股份有限公司经济师 ,管理学硕士。研究方向:项目管理。魏秋建,台湾中华大学管理学院教授。研究方向:项目管理、知识管理。