我国超大城市碳排放与经济增长关系的实证研究

李云燕　赵国龙

(北京工业大学，北京　100124)

我国超大城市碳排放与经济增长关系的实证研究

李云燕赵国龙

(北京工业大学，北京100124)

〔摘要〕城市经济发展离不开能源消费，而能源消费直接导致大量的碳排放，深入研究碳排放与经济增长之间关系对超大城市实施节能减排、发展低碳经济具有重要意义。本文分别选取了上海市、北京市、天津市和重庆市1995～2014年碳排放和经济增长的相关数据，对两者的脱钩关系和格兰杰因果关系进行实证研究，得出长期内实施碳减排政策不会阻碍超大城市经济增长的结论。因此，超大城市应该积极推动低碳城市建设，不断推动产业结构升级，改善能源消费结构，积极实施节能减排政策和倡导低碳生活。

〔关键词〕超大城市碳排放经济增长脱钩状态格兰杰因果检验

全球气候变暖问题已引起国际社会的广泛关注，《联合国气候变化框架公约》第21次缔约方会议于2015年11月在法国巴黎举行，顺利达成全球气候变化新协定——《巴黎协定》(近200个缔约方一致同意通过)，并对2020年后全球应对气候变化行动作出安排。该协定主要包括目标、适应、减缓、技术、资金、透明度、损失损害、能力建设、全球盘点等29条内容，与会各国均作出碳减排目标的承诺。

自改革开放30多年来，中国城市化和工业化的快速推进，造成能源大量消耗和污染物过度排放，中国经济社会发展与资源环境约束之间的矛盾愈发显现，生态环境问题突出。城市能源消费量占到全球能源消耗的75%以上，温室气体排放量也占到全球近80%。国务院在2014年11月印发《关于调整城市规模划分标准的通知》，将城市划分为5类7档，其中超大城市划分的依据是指城区常住人口1000万以上(注：城区包括市辖区、不设区的市，以及区、市政府连接到的居民委员会所辖区域等)。根据新标准，人口在1000万以上的城市有6个(即北京、上海、天津、重庆、广州、深圳)。这类城市对城市建设要求很高，其发展水平基本达到国际化水准，不仅在区域经济增长方面发挥引擎作用，而且在控制碳排放方面发挥突出作用。在超大城市范围内，推行清洁生产、循环经济、节能减排、低碳城市建设等低碳发展路径，有助于解决当前城市面临的能源危机、环境危机，显着提高超大城市的国际影响力和竞争力。目前，我国经济社会发展已进入新常态，呈现出经济增长速度适宜、结构优化、社会和谐等趋势。超大城市在保持城市经济社会发展的同时，提出一系列减碳政策并制定行动计划，在碳排放方面也取得了卓有成效的成果。本文研究超大城市碳排放与经济增长内在关系，主要考虑到低碳经济未来国际发展新趋势，以及超大城市在目前中国经济社会发展中扮演的重要角色，加强低碳城市建设，实现经济社会的可持续发展。

20世纪70年代发生的石油危机引起专家学者对能源消费与经济增长关系的研究，随着环境污染问题突出和公众环保意识增强，碳排放引起国内外专家学者的关注，能源消费、碳排放与经济增长三者之间的关系受到重视。

1.1理论研究方面

Galeottia和Lanza在内生技术进步的经济增长框架下研究了100多个国家近25年的统计数据，探究技术进步、生态污染与经济增长三者之间的关系，得到二氧化碳排放与经济增长两者之间的环境库兹涅茨曲线，根据曲线特征并提出了经济增长的最优路径[1]。20世纪90年代，Grossman，Kruege最早提出经济增长对环境效益影响的3种路径，即规模效应、结构效应和技术效应。其中，规模效应是指随着经济增长要求各类能源、资源的大量投入，但化石能源的大量消耗导致污染物的过度排放；结构效应是指经济持续增长将促使产业结构和能源消费结构发生变化，而不同的产业结构和能源消费结构对环境影响差别很大；技术效应是指环境保护产业将吸收更多的资源来促进经济增长，同时污染处理的技术水平得到提高[2]。

1.2实证研究方面

受计量经济学的发展局限，各阶段实证研究所采用的方法有所不同：最初，在VAR研究模型基础上，运用传统格兰杰Granger和质谱分析Sims等因果检验方法，例如Kraft等学者采用双变量Sims因果检验方法[3]，结果表明美国(1947～1974)存在从经济增长到能源消费单向因果关系，即经济增长可能导致碳排放量增加。之后，协整理论和误差纠正模型被应用到能源消费和经济增长关系的实证检验。例如，Yu和Jin研究美国1974～1990年间两者能源消费和经济增长关系时采用季度数据，运用E-G两步法，结果表明两者之间不存在任何方向因果关系[4]；Glasure等选取韩国和新加坡1961～1990年的年度数据，运用了双变量误差纠正模型，最终表明两国能源消费和经济增长两者具有双向因果关系[5]；Soytas和Sari[6]构建了能源消费和生产总值双变量误差纠正模型，结果发现16个国家的能源消费和生产总值之间具有非固定性关系，但也表现出显着差异性，有7个国家具有固定线性协整关系，各国碳排放与经济增长之间格兰杰因果关系检验结果并不一致。Asafu-Adjaye研究了亚洲部分发展中国家的能源价格、能源消费量和经济增长三者之间的关系，得出印度和印尼两国能源消费到经济增长存在单向因果关系，但泰国和菲律宾两者具有双向因果关系[7]。2005年之后，面板单位根检验、协整检验和因果关系检验等方法被采用。面板数据计量方法不仅提高样本数据容量和自由度，还能减轻异方差和共线性等影响，提高数据估计有效性。Lee根据18个发展中国家1975～2001年的统计数据，采用异质面板协整和因果检验方法，研究得出：无论从长期还是短期考虑，这些发展中国家的能源消费到经济增长都具有单向因果关系[8]。

国内外研究碳排放与经济增长关系大都基于一个国家或特定地区，但不同国家或地区经济总量和经济社会发展水平差异性较大，同样的研究思路和方法可能得出相反的研究结论。Richmond、Marzio Galeotti等均采用CKC曲线模拟、检验和分析了经济合作发展组织(OECD)国家。Soytas等研究美国能源消费、收入和碳排放之间的关系，得出能源消费直接导致了二氧化碳碳排放增加，但经济增长不一定引起二氧化碳碳排放增加[9]。基于某个国家的实证研究，由于统计数据便利性、一致性，很多学者主要选取一个国家进行经济计量统计研究。由于各个国家有不同的经济发展特征，也会造成碳排放与经济增长关系之间不同的研究结论，甚至处于同一经济发展水平的国家，长期来看两者之间也会有不同的经济动态作用。

2.1碳排放与经济增长脱钩模型构建

2.1.1脱钩模型的构建

常见的两种脱钩模型：Tapio模型和OECD模型。Tapio模型有关弹性指数的划分更为精细，更清晰地反映经济增长与碳排放在不同地区不同时间或同一地区不同时间表现的脱钩状态，且Tapio模型对时间基期选择要求低，且不易受指标量纲的影响。因此，本文构建Tapio模型研究4个超大城市碳排放和经济增长之间的脱钩关系，即：

(1)

该式中，wn是脱钩弹性指数，RΔC是碳排放量增长率，即碳排放水平第n年相对于第n-1年的变化率，RΔGDP则指某超大城市第n年的地区生产总值相对第n-1年的变化率。

2.1.2脱钩状态的表示

根据脱钩弹性指数的不同特征，Tapio将脱钩状态划分为8种类型[10]，如表1，转化到空间直角坐标为图1。我国正处于经济快速发展过程中，经济增长率一定大于零，因此脱钩只会位于第一、四象限，存在强脱钩、弱脱钩、增长连结和扩张负脱钩4种脱钩状态。

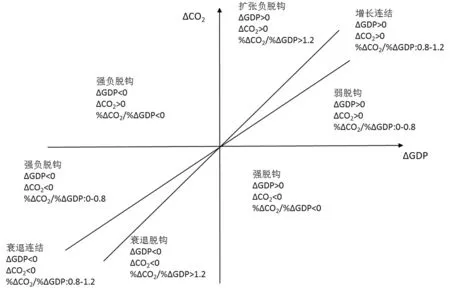
图1　经济增长与碳排放的脱钩状态

2.2格兰杰因果关系检验模型

2.2.1单位根检验

单位根检验的目的是检查时间序列的平稳性，避免分析中伪回归发生，它也是分析各变量之间是否存在协整关系和进行格兰杰因果关系的前提。本论文采用ADF检验方法，该方法是由DF检验(Dickey-Fuller检验)基础上发展而来，DF检验仅适用于1阶自回归过程的检验，ADF检验能够适用于多阶AR(p)过程的平稳性检验。

ADF检验原理，以1阶自回归序列为例：xt=φxt-1+αt

该序列特征方程为：λ-φ1=0

当特征根φ1在单位圆内时，该序列是平稳的；反之，则说明该序列是非平稳的。

原假设H0：序列xt是非平稳的；备泽假设H1：序列xt是平稳的。

(2)

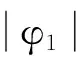
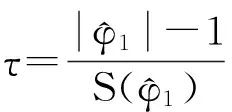
在进行ADF检验之前，可先对时间序列进行初步判断，可用时序图初步判断时间序列是否不平稳，为避免数据较大程度的波动性，容易得出平稳序列，本论文可以将生产总值GDP和二氧化碳排放CO2分别取对数，可分别记为LNCO2和LNGDP。本论文采用Eviews 8软件进行ADF检验。

2.2.2协整检验

协整检验是对非平稳序列的因果关系检验，协整即存在共同随机性趋势，对序列进行协整处理主要是检验变量之间是否存在稳定的关系，防止非平稳序列引起的伪回归。1978年，Engle和Granger提出协整理论[11]，如果两个随机游走的变量序列的某个线性组合为稳定的，则这两序列是协整的，两个序列单整阶数相同，是两序列之间存在协整性的必要条件。

若已知两个序列xt和yt为非平稳的，但都是d阶单整序列，那么就可以用协整回归方程(OLS)：xt=α+βyt+εt的残差εt是否存在平稳的检验判断xt和yt协整性，若xt和yt不存在协整，则其任意一个线性组合均为非平稳，即残差εt必然也是非平稳。所以，若检验表明残差εt为平稳的，那么我们可以认为xt和yt之间具有协整关系。

2.2.3格兰杰因果关系检验

格兰杰检验仅是对平稳时间序列的一种预测，假设有两个经济变量C(碳排放量)和G(GDP)，在同时包含两者信息的条件下，对于变量C的预测效果，一般优于仅单独由C过去信息来对C的预测效果，即变量G有助于改善对变量C的解释和预测准确性，那么则认为变量X和Y之间存在格兰杰因果关系。两变量的自回归模型为：

(3)

(4)

要对βi(i=1，2，…，m)=0进行检验，即“G不是导致C变化的原因”，同样拒绝βi(i=1，2，…，m)=0原假设，也就是肯定了从G到C的格兰杰因果关系；同理，βj(j=1，2，…，m)=0假设则是验证Y到X的格兰杰因果关系。

此外，我们必须注意到格兰杰因果关系检验仅仅是进行统计意义上的判断，并不代表真正意义上的因果关系，因此不是简单地肯定或否定最终因果关系的依据[12]。格兰杰因果关系检验的前提是只能用于平稳序列的检验，其结论并非保证实际存在的因果关系，但仍有重要参考价值，尤其在与经济预测方面起到很大的作用。

2.3二氧化碳碳排放测算方法

基于能源消费的碳排放核算方法有很多，常用的有3类：基于能源平衡表、基于一次能源消费量和基于终端能源消费量的能源消费碳排放核算方法，不同的能源碳排放方法将导致最终的核算结果出现很大差异，主要原因在于排放因子选择、碳氧化水平及加工转换过程的不确定性影响[13]。

根据IPCC提供的碳排放计算公式，并结合超大城市能源统计数据特点，本文基于一次能源消费量的碳排放核算方法，采用以下公式计算碳排放量：

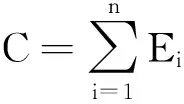
(5)

式中，C代表碳排放总量，单位104t；Ei代表能源i的消费量，根据不同能源计量标准核算，Ci为能源i的二氧化碳排放系数(表略)；i为能源种类。本论文在计算碳排放时不将电力、热力纳入核算范围，只考虑一次能源的碳排放。

3.1超大城市经济增长比较分析

本文选取上海、北京、天津、重庆4个超大城市作为研究对象，如图2，各城市之间地区GDP差距较大，2014年上海市GDP是重庆市的近2倍，而上海市和北京市总量相当，天津市和重庆市总量相当。如图3，各城市历年GDP增长率，总体处于较高水平，但各年增长率都处于较大波动，自2010年开始4个城市增长率均出现不同程度下降，上海市和北京市自2012年开始增长率进入8%以下，但经济增量依然很大；相比，天津市和重庆市增长率仍然处于高位，大大高于全国平均水平。

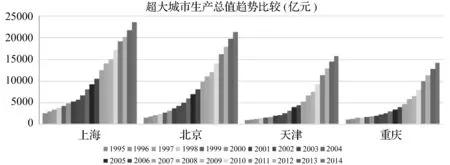
图2　超大城市地区GDP趋势(1995～2014)

3.2超大城市碳排放比较分析

本文采用一致的碳排放测算方法，主要基于一次能源中主要能源消费品种的碳排放系数换算得来。如图4，上海市二氧化碳排放量最高，这与能源消费总量变化趋势基本一致，而北京市二氧化碳排放量整体变化不大，主要源于能源结构的改善，二氧化碳排放系数较高的煤炭、焦炭、燃料油消费量下降明显，天然气消费量上升明显(约是天津的2.5倍)；天津市二氧化碳排放水平高于北京、重庆的原因，在于以煤炭、焦炭、原油等高排放为主的能源消费结构；重庆市二氧化碳排放低于天津市的原因，在于焦炭使用量不高，由于统计口径或数据缺陷原因，重庆市原油使用量极其少，这是造成其二氧化碳排放水平较低的主要原因。如图5，4个城市单位GDP碳排放量逐年减少，北京市下降幅度最为明显，由1995年6.45吨/万元下降到2014年的1.28吨/万元，是目前单位GDP碳排放最小的城市，其次是上海市、重庆市和天津市，其中天津市单位GDP碳排放一直处于较高水平。

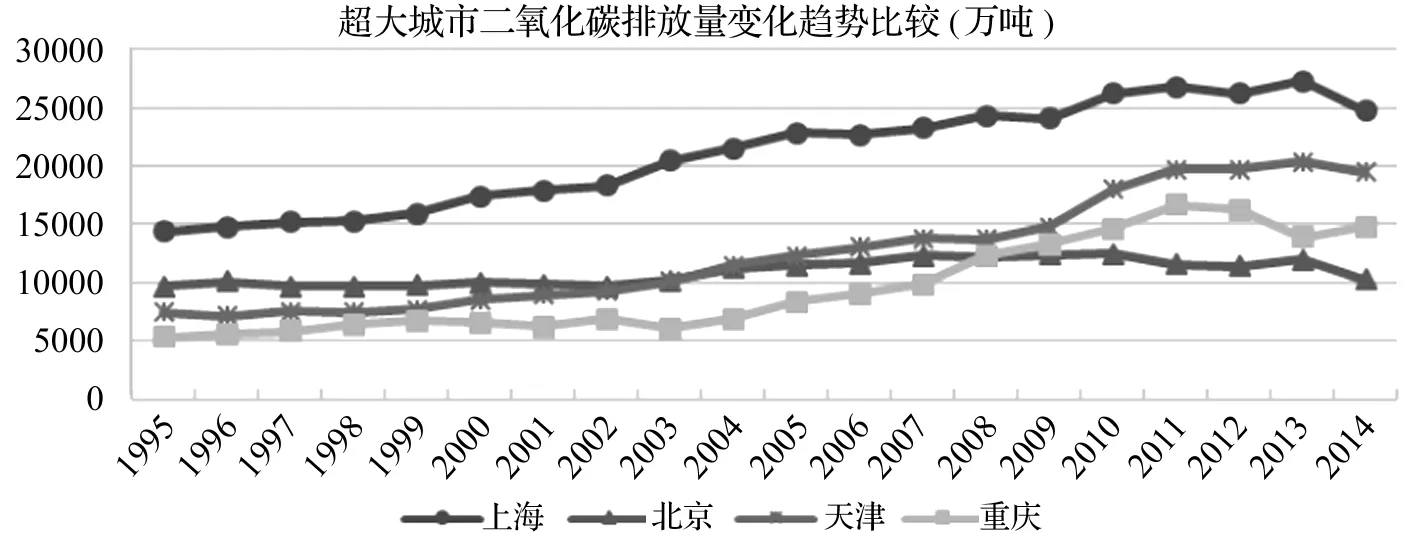
图4　超大城市历年二氧化碳排放量变化趋势(1995～2014)

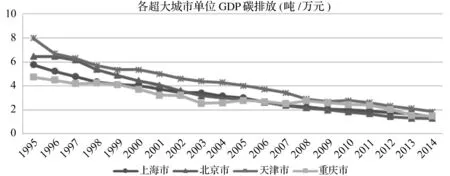
图5　超大城市单位GDP碳排放变化趋势(1995～2014)

基于统一的碳排放计算公式和各城市常住人口总数可以得出人均二氧化碳排放量，如图6，重庆市人均二氧化碳排放量最低，但近几年呈现不断上涨趋势，(1)重庆市常住人口基数大，近20年变化不明显；(2)总体经济体量近几年增长速度快，带动能源消费量不断攀高，但碳排放水平仍处于较低水平，若考虑重庆市森林碳汇，其人均二氧化碳排放量还会更低；近年来，天津市人均二氧化碳排放量处于较高水平，主要在于煤炭、焦炭等碳排放系数较高的能源消费增长过快，这与天津市三次产业中第二产业比重近50%有关，而能源消费占比中第二产业超过70%。

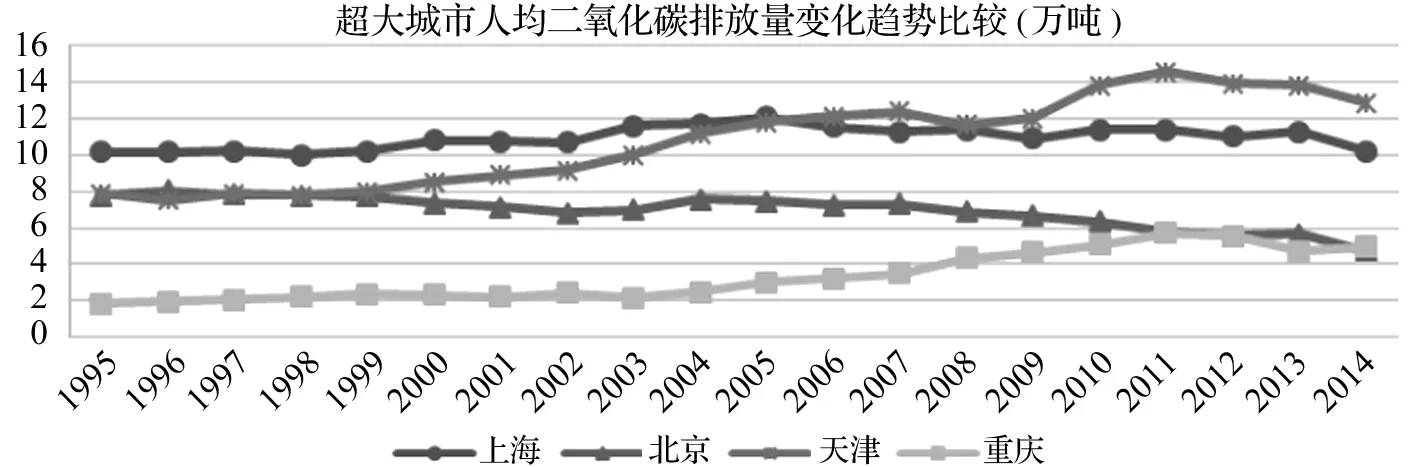
图6　超大城市人均二氧化碳排放量变化趋势比较(1995～2014)

4.1碳排放与经济增长脱钩分析

根据上述脱钩模型分别计算得到上海市、北京市、天津市和重庆市1995～2014年间碳排放与经济增长脱钩状态图7～10，4个超大城市大部分年份位于弱脱钩状态，表示经济增长的速度明显快于碳排放增加速度。其中，北京市脱钩状态最好，强脱钩年份较多，且其脱钩弹性系数较小，从时间序列来看，脱钩呈现良好势头发展，自2008年以来强脱钩年份增加，说明北京市节能减排政策取得良好效果。而上海市的脱钩状态与北京市类似，历年脱钩状态均位于弱脱钩和强脱钩区域，说明经济的高速增长并未带来碳排放量的过快增长。

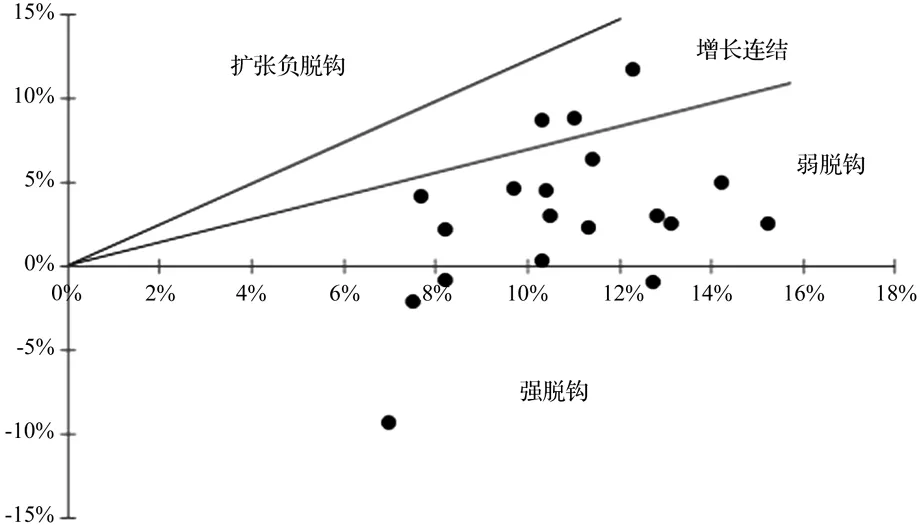
图7　上海市1995～2014年碳排放与经济增长脱钩状态

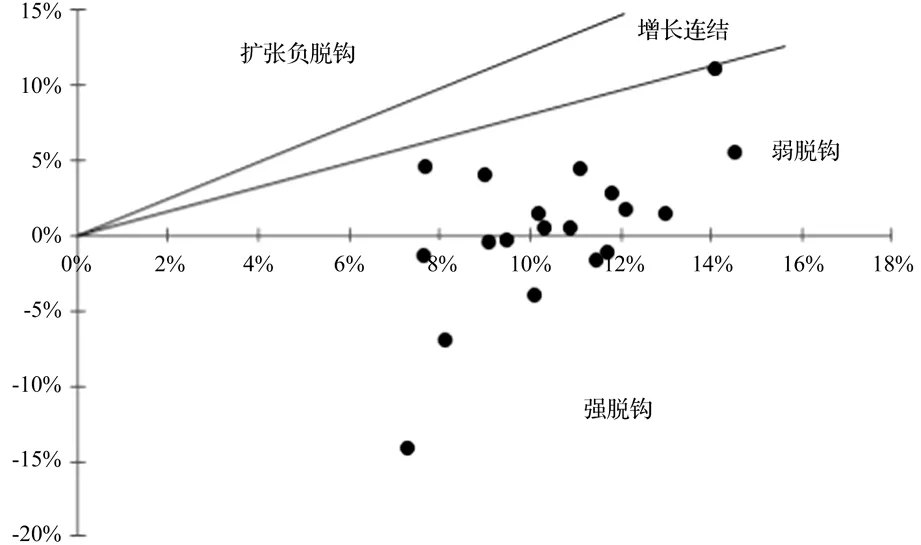
图8　北京市1996～2014年碳排放与经济增长脱钩状态

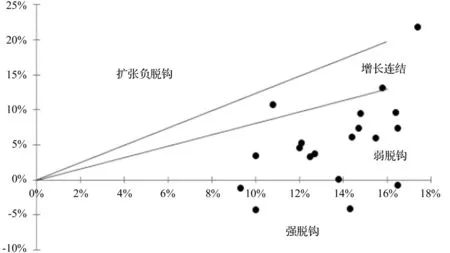
图9　天津市1994～2014年碳排放与经济增长脱钩状态

天津市和重庆市的脱钩状态较为一致，从时间序列上看脱钩状态年际变化大；从整体分布上看，大部分年份弱脱钩状态表现并不明显，脱钩系数值较大，说明经济增长同时伴随碳排放量增加。这与两座城市正处于快速发展的时期有关，也与三次产业中第二产业比重占有重要位置有关，而第二产业是能源消费的主要来源，也是导致碳排放增加的根源。

4.2格兰杰检验

4.2.1单位根检验(ADF检验)——以上海市为例

(1)根据4个超大城市碳排放与经济增长时间序列数据得到各城市GDP与CO2时间序列图，可以看出1995～2014年间各城市经济均处于高速增长水平，但碳排放年际变化差异较大，其中北京市碳排放量波动较小，且处于下降趋势。

(2)为保证时间序列数据的平稳性，分别对4个超大城市LNCO2和LNGDP进行平稳性检验，本文采用ADF检验方法，滞后期数为2，检验原理参照前述要求。例如表2为上海市ADF单位根检验结果，在5%的显着水平下t统计量为0.992746，其P值大于显着性水平α，所以接受原假设，即GDP时间序列数据为非平稳序列，且LNGDP一阶差分后仍然接受原假设。当对LNGDP进行二阶差分时，5%显着水平下的t统计量为-5.647835，小于显着性水平α，拒绝原假设，即LNGDP为二阶单整序列，显着性水平为1%。同理，LNCO2为二阶单整序列，显着性水平为1%。

续　　表

同理，得到北京市在1%显着水平下，LNGDP和LNCO2均为二阶单整序列。天津市在1%的显着水平下，两者均为二阶单整序列。重庆市LNGDP为二阶单整序列，LNCO2为一阶单整序列。

4.2.2协整检验分析——以上海市为例

根据ADF检验结果，若LNGDP和LNCO2在不同显着性水平下为平稳时间序列，说明可能存在协整的长期稳定均衡关系，因此可以对其进行协整检验分析。其中上海市协整回归结果如表3，用Eviews软件对LNGDP和LNCO2时间序列数据做协整分析，以为LNCO2因变量，LNGDP为自变量，进行OLS(最小二乘估计)回归分析得到协整回归方程为：

LNCO2=6.845602+0.348285LNgdp+ut

R2=0.96，F=416.84，DW=0.875660，自变量的系数通过检验，说明回归方程具有较高的显着性。从协整方程来看，经济总值GDP增长的估计系数是0.348285，表示GDP每增加一个单位，二氧化碳CO2排放会增加0.348285。对残差进行ADF检验，结果表明残差序列 为平稳序列，Eviews软件操作结果如表3和表4。

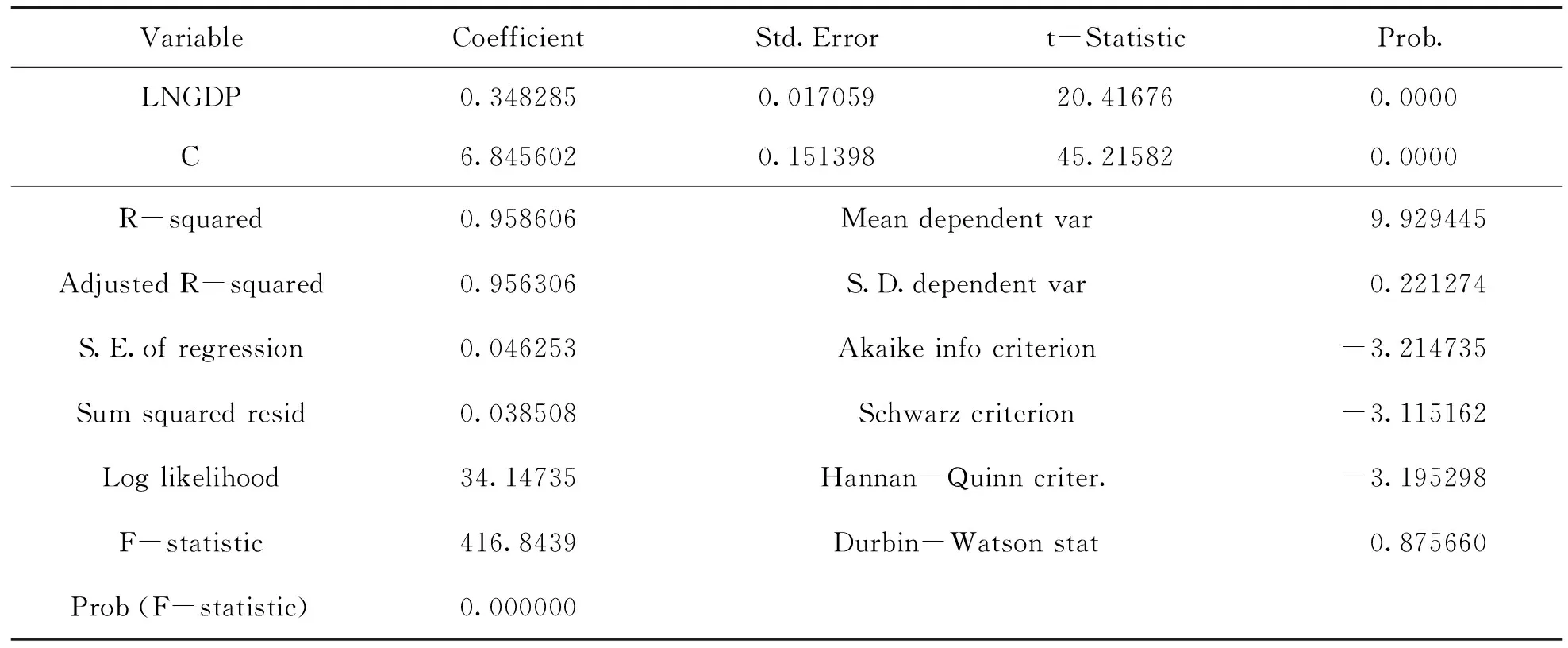
表3　上海市碳排放量与GDP协整回归结果

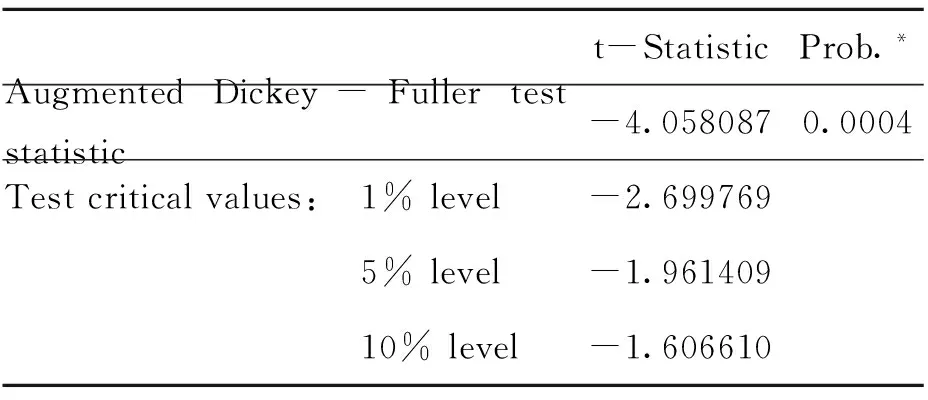
表4　上海市碳排放量与GDP协整回归残差的ADF检验结果

4.2.3格兰杰因果关系检验

根据前述原理，分别对4个城市LNCO2和LNGDP进行格兰杰因果性检验，遵从SC和AIC最小化准则，我们确定格兰杰因果性检验的滞后期为2，检验结果如表5所示，上海市的两个假设的显着性概率均大于0.05，接受原假设，即上海市经济增长GDP和二氧化碳排放之间不具有因果关系。同时，反映出上海市经济增长处于可持续发展路径上，经济的持续增长不会引起二氧化碳排放量的增加，二氧化碳的排放也不会导致经济增长。北京市检验结果与上海市类似，而天津市和重庆市检验结果一致，即存在经济增长到碳排放的单向格兰杰因果关系，经济增长是二氧化碳排放的格兰杰原因，反之则不成立，实施碳减排措施，长期来看并不会阻碍经济的增长。

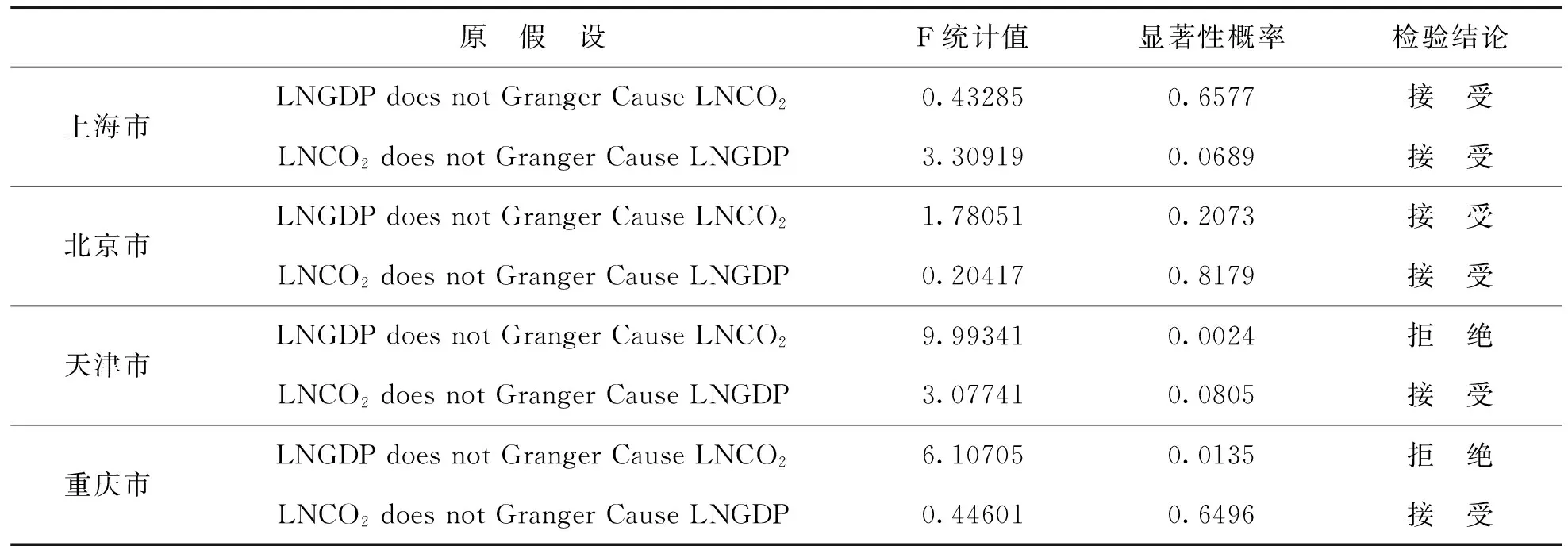
表5　格兰杰因果关系检验结果

(1)通过比较分析和实证研究，4个超大城市的碳排放与经济增长脱钩状态以弱脱钩为主，其中北京市脱钩状态最佳，脱钩趋势逐渐由弱脱钩向强脱钩转变，天津市和重庆市各年脱钩状态变化较大。通过格兰杰因果关系检验发现，上海市和北京市检验结果较为一致，表明碳排放和经济增长两者不具有格兰杰因果关系，而天津市和重庆市表现出经济增长到碳排放的单向格兰杰因果关系，说明长期来看，碳排放的增长并不会导致经济的增长，即实施强有力的节能减排措施，长期内不会导致经济下滑。

(2)通过超大城市内部经济结构和碳排放的差异分析，经济的快速增长并不一定引起能源消费量的增加，主要在于产业结构是否合理、能源效用效率是否不断提高，上海市和北京市经济发展水平较高，更加注重经济发展质量。能源消费量的增加并不一定导致碳排放增加，主要在于能源消费结构是否改善，天津市和重庆市以煤炭为主的能源消费结构，势必导致碳排放的大量增加。

(3)城市是中国经济发展和人们生活最为集中的区域，同样也是能源消费和污染物排放最为集中的区域，因此，发展低碳经济就需要重视低碳城市建设。其中，政府在低碳城市建设中起到主体作用，也是经济结构转型推广低碳经济的推动者。实现城市的低碳化，必须努力从推行低碳经济和实现低碳生活这两个方面入手。实现城市经济发展的低碳化，可以从经济发展方式转变、经济发展结构调整、经济发展能源以及节能减排新技术的政策扶持等4个方面进行努力；实现城市社会生活的低碳化，必须要积极宣传普及低碳生活的理念，实现低碳城市规划，推广建筑节能实现绿色建筑，加强城市的绿化建设来提高城市森林覆盖率[15]。

(4)我国超大城市在引领区域经济社会发展中起到风向标的导向作用，建设低碳城市是一项系统性工程，需要政府、企业和公众的广泛深层次参与。超大城市应明确自身经济发展总体定位，构建完善的城市发展体系，科学规划城市发展路线，积极合理建设超大城市交通体系，实现与周边地区的良性经济互动，引领周边城市群的低碳建设之路。通过调整能源消费结构、优化产业结构、提高资源使用效率，能够最大限度的降低碳排放水平。要不断加强新能源开发利用，提高可再生能源的比率，例如推进供热煤改气等清洁转型，鼓励可再生能源技术研发和应用[16]。同时，完善节能减排相关政策法规和标准，建立健全超大城市调控和决策机制，例如加强节能减排目标的考核和监督力度，建立区域能源管理联动机制和消费总量预测预警机制。

参考文献

[1]Galeotti M,Lanza A.Desperately Seeking Environmental Kuznets[J].Environmental Modelling & Software.2005,20(11):1379～1388

[3]Kraft J,Kraft A.On the Relationship Between Energy and GNP[J].Journal of Energy and Development，1978，(3):401～403

[4]Yu,H E S,Choi,et al.The Causal Relationship Between Energy and GNP:An International Comparison[J].Journal of Energy and Development，1985,10(2):249～272

[5]Glasure,U.Y,Lee,et al.Cointegration,Error-correction,and the Relationship Between GDP and Electricity:The Case of South Korea and Singapore[J].Resource and Energy Economics，1997,20:17～25

[6]Soytas U,Sari R.Energy Consumption and GDP:Causality Relationship in G-7 Countries and Emerging Markets[J].Energy Economics，2003,25(1):33～37

[7]Asafu-Adjaye J.The Relationship Between Energy Consumption,Energy Prices and Economic Growth:Time Series Evidence from Asian Developing Countries[J].Energy Economics，2000,22(6):615～625

[8]Lee C.Energy Consumption and GDP in Developing Countries:A Cointegrated Panel Analysis[J].Energy Economics，2005,27(3):415～427

[9]Soytas U,Sari R,Ewing B T.Energy Consumption,Income,and Carbon Emissions in the United States[J].Ecological Economics，2007,62(3-4):482～489

[10]Tapio P.Towards a Theory of Decoupling:Degrees of Decoupling in the EU and the Case of Road Traffic in Finland Between 1970 and 2001[J].Transport Policy，2005,12(2):137～151

[11]Engle R F,J G C.Cointegration and Error Correct Ion:Representation,Estimation,and Testing[J].Econometria，1987,55:251～276

[12]武红，谷树忠，关兴良，等.中国化石能源消费碳排放与经济增长关系研究[J].自然资源学报，2013,(3):381～390

[13]刘竹，耿涌，薛冰，等.城市能源消费碳排放核算方法[J].资源科学，2011，(7):1325～1330

[14]王小斌，邵燕斐．中国城镇化、能源消耗与二氧化碳排放研究——基于1995～2011省级面板数据[J]．工业技术经济，2014，(4)：115～123

[15]李云燕，赵国龙.中国低碳城市建设研究综述[J].生态经济，2015，(2):36～43

[16]吴振信，万埠磊.基于环境库兹涅茨曲线的北京市碳排放与经济增长相关性研究[J].经济研究导刊，2012，(14):61～64

(责任编辑：史琳)

The Empirical Study on the Relationship between Carbon Emissions and Economic Growth in Megacity Behemoths

Li YunyanZhao Guolong

(Beijing University of Technology，Beijing 100124，China)

〔Abstract〕The development of city economy depends on huge exhaustion of energy,but it can directly lead to the increase of carbon emissions.The empirical study on the relationship between carbon emissions and economic growth is of great significance for megacity behemoths to implement energy conservation and emissions reduction,development of low carbon economy.This paper selects the Shanghai-Beijing-Tianjin-Chongqing data on carbon emissions and economic growth from 1995 to 2014,to study their decoupling relations and granger causality.It is concluded that implementation of carbon reduction policy will not hinder economic growth of the megacity behemoths in the long term.Therefore,megacity behemoths should actively promote low-carbon urban construction,constantly promote the upgrading of industrial structure,improve energy consumption structure,active implementation of energy conservation and emissions reduction policy and advocate low carbon life.

〔Key words〕megacity behemoths;carbon emission;economic growth;decoupling relations;Granger causality test

〔中图分类号〕F290

〔文献标识码〕A

DOI：10．3969/j．issn．1004-910X．2016．10．018

作者简介：李云燕，北京工业大学循环经济研究院教授，博士，博士生导师。研究方向：环境经济学、环境管理与规划。赵国龙，通讯作者，北京工业大学循环经济研究院硕士研究生。研究方向：环境经济学。

基金项目：国家社科基金项目“基于DPSIR模型框架的京津冀雾霾成因分析及综合治理对策研究”(项目编号：15BJY059)；北京市社科基金项目“京津冀地区PM2.5污染控制政府绩效评估模式的构建”(项目编号：14JGB036)。

收稿日期：2016—05—15