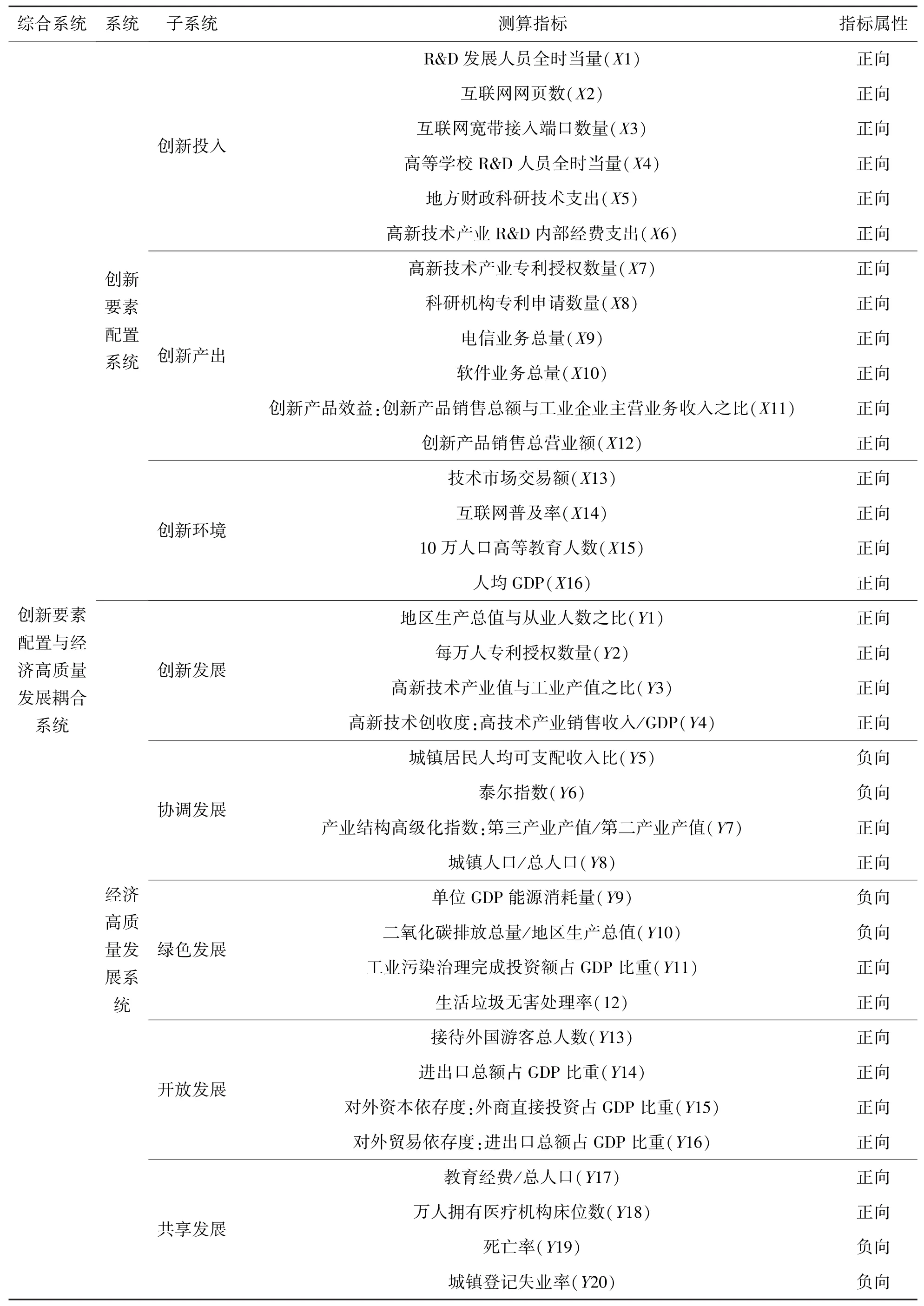
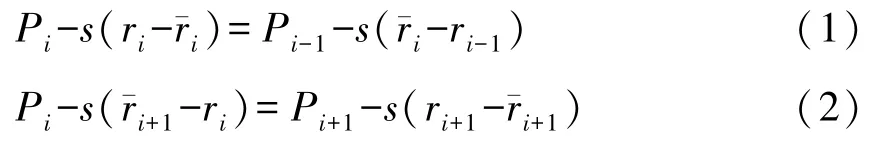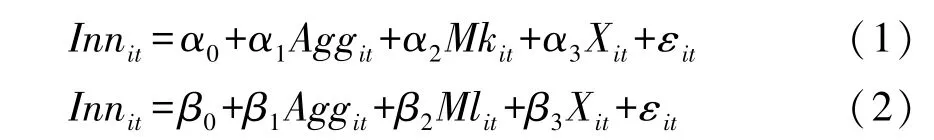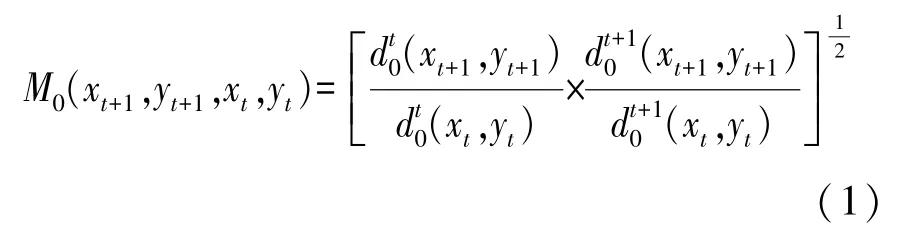苏 华 王威华 肖 飒
(兰州大学经济学院,兰州 730000)
黄河流域是我国重要的经济地带,也是打赢脱贫攻坚战的重要区域,要促进全流域高质量发展,就需要构建高质量发展的动力系统。高质量发展意味着经济运行必须是效率和质量导向的,即体现质量第一、效率优先的原则[1]。关于高质量发展的路径,习总书记在中央财经委员会第五次会议上强调,“要发挥各地区比较优势,促进各类要素合理流动和高效集聚,增强创新发展动力”。而长期以来,由于我国行政区域的割裂和地方政府竞赛的特征事实,生产要素流动受到限制[2]。为促进区域经济协调发展,实现地区之间的生产要素自由流通,国家相继规划了多项发展战略。继粤港澳大湾区和长江经济带一体化后,黄河流域生态经济带也步入国家战略规划的范畴,以生态保护和高质量发展作为其发展的主旋律。由此可见,如何利用要素集聚推动黄河流域生态经济带的高质量发展亟待研究。基于此背景,本文试图构建黄河流域生态经济带要素集聚与高质量发展的Cobb-Douglas模型,分析要素集聚对黄河流域经济带高质量发展的作用机制,在此基础上运用该地区2003~2018年地级市面板数据对其进行实证检验,以期为黄河流域经济带的高质量发展决策提供参考。
1 文献综述经济集聚已成为工业革命以来普遍的生产活动。 自 Krugman Paul(1991)、 Fujita 和 Mori(2005)新经济地理学派和罗默卢卡斯等新增长学派将外部性引入集聚的分析框架中以来,经济集聚研究得到了充分发展[3,4]。 Henderson (1997) 更进一步将外部性分为产业专业化和产业多样化,其中产业专业化也被称为 “Marshall-Arrow-Romer型外部性”,而产业多样化则被称为“Jacobs型外部性”[5]。在认识到集聚经济所具有的外部性后,部分学者开始将集聚与经济增长联系起来,探讨集聚与经济增长之间的作用机制。具体来说,集聚对经济增长的作用机制大致可以分为两个方面: (1)经济集聚可以通过溢出效应从而推动技术创新,进而起到促进经济增长的作用,如Martin和Ottaviano(1999)、 Fujita和 Thisse (2003)、 Dupont (2007)的研究多强调集聚的溢出效应[6-8],如人力资本等因素的作用; (2)经济的空间集聚引起的交易成本降低和要素流动提高了要素利用效率,如Krug⁃man Paul(1991)、 Puga(1998) 的研究成果[3,9]。
而在实证方面的研究也证明了集聚对经济增长有正向的促进作用。如Ciccone和Hall(1996)、Ciccone(2002)、范剑勇 (2006)使用反应经济集聚度的就业密度与和经济增长相关的劳动生产率验证了集聚对经济增长的作用大小[10-12]。 Otta⁃viano和Pinelli(2006)以人口密度来衡量经济集聚水平,并对地区收入进行回归,同样得出了相同的结论[13]。 Henderson (2003) 以城市化水平作为经济集聚的衡量标准,采用跨国数据实证发现了经济集聚对发展中国家经济增长的促进作用的事实[14]。当然,也有研究从产业集聚作为切入点,实证探讨产业集聚对经济增长的作用,如Mitra和Sato (2007)[15]、 韩峰和柯善咨 (2012)[16]、 张海峰和姚先国(2010)[17]、 原毅军和宋洋(2011)[18]、曹聪丽和陈宪 (2017)[19]。这些研究无一例外,认为经济集聚对经济增长具有促进作用。
随着研究的深入,部分学者发现集聚对经济增长并非总是促进关系。经济集聚同时存在溢出效应与拥挤效应。初期,当拥挤效应小于溢出效应时,反映为集聚对经济增长的正向作用,由于集聚往往具有循环累积的效应,当集聚所产生的交通拥挤、房价提升等负效应大于外溢效应时,集聚便阻碍了经济增长[20]。因此,区域内集聚效应与拥挤效应二者的均衡会最大程度发挥集聚的优势[21]。孙浦阳等 (2011)采用国别数据证明了集聚的外部性大小会随着国家经济的发展而逐渐减弱,进而提出处于发展初期的国家更应该支持经济集聚的建议[22]。随后刘修岩等 (2012)采用我国地级市的数据再次验证了该观点,得出当前我国经济集聚存在着不经济的现象[23]。蔡武等 (2013)通过在城市函数中引入空间集聚外部性,探讨了产业集聚和劳动力流动影响城乡收入差距的内在机理和具体路径,并验证发现了农村劳动力影响城乡收入差距的轨迹伴随城市产业集聚规模的变化呈现出倒 “U” 型的特征[24]。
通过对文献的梳理不难发现,国内产业集聚已经成为经济发展过程中的一个典型化事实[25-28]。然而,在实证研究方面,针对集聚与我国经济增长的研究表明,两者关系十分复杂,且研究产业集聚的相关文献偏多,而侧重要素集聚的研究,集聚的指标选取多偏向就业密度、人口密度等衡量指标,对集聚的衡量并不十分全面和准确。且考虑到高质量发展,国内已有部分学者进行了深入细致的研究,并认为创新驱动和劳动生产率的提升是衡量高质量发展的标准[29,30]。因此,创新一时成为热点话题。由于创新的基础在于人力资本,因此各地纷纷上演轰轰烈烈的 “抢人大战”。创新应符合自身的禀赋条件[31],各地区由于自身禀赋条件不同,高质量发展的涵义也应有所区别。因此,本文选取人力资本集聚和要素禀赋集聚作为集聚的代理变量,充分考虑人均物质资本存量对地区高质量增长的影响。本文的研究范围是黄河流域生态经济带,探究黄河流域生态经济带内要素集聚对高质量发展的作用机理,对促进黄河流域区域经济一体化、缩小区域发展不平衡有重要意义。
2 模型的构建2.1 理论模型的构建本文利用Cobb-Douglas模型对要素集聚与经济增长进行研究,假定要素集聚所产生的外部性将作用于模型的全要素生产率,理论模型设计如下:

其中Y表示总产出,H是人力资本集聚指标,k则表示禀赋集聚指标。从式 (1)中可以发现,全要素生产率受到人力资本集聚和基础禀赋集聚两方面的影响,该影响体现于式中A(H,k)一项,为满足生产函数的规模报酬递增性质,该式将全要素生产率定义为希克斯中性。
Benhabib和Spiegel(1994)将全要素生产率的变动归结为地区的技术创新行为和其对技术领头地区先进技术的追赶行为[32]。人力资本对技术创新的作用已经得到学界广泛的认可,而技术追赶行为,则表现为对技术先进地区的技术模仿。当然,一个地区的创新结构应与其自身的禀赋结构相匹配,否则若盲目地进行模仿创新,企业只会在市场上失去自生能力[31],从而背离了高质量发展的初衷。故本文选择人力资本集聚表征当地的创新产出水平,用基础禀赋表征当地对其他地区先进技术的吸收效应。
借鉴 Hulten 等 (2006)[33]、 刘生龙和胡鞍钢(2010)[34]的研究成果, 本文假定式 (1) 中希克斯效率项及其组成部分可以进行多元组合,因此,可将式 (1)改写成如下形式:
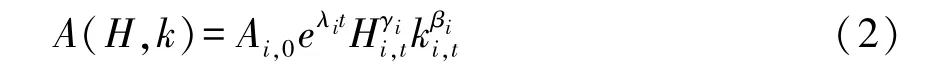
将式 (2)带入式 (1)中,便可得到:
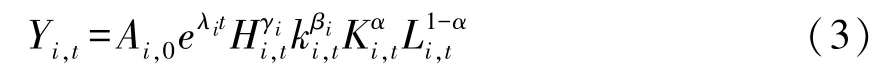
其中,式 (3)中的i表示不同的区域,而t则表示时间因素。Ai,0代表初始的生产效率,λi用来代表外生的技术变迁作用,而参数γi代表人力资本集聚对经济效率作用,βi则表示要素禀赋集聚对经济效率的作用。其中,γi和βi是需要关注的主要参数。
将式 (3) 两边同时除以F(Ki,t,Li,t), 得到如下结果:
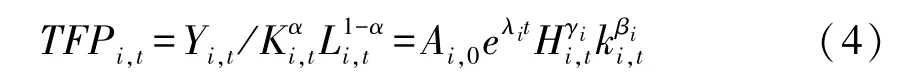
将式 (4)两边同时取自然对数,得到人力资本集聚和自然禀赋集聚作用于全要素生产率的方程:
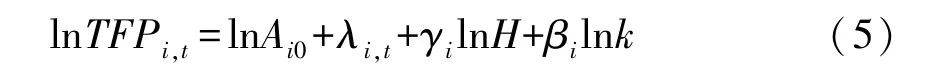
考虑到其它变量也会对全要素生产率产生影响,因此本文在式 (5)的基础上,加入控制变量,得到如下计量模型:
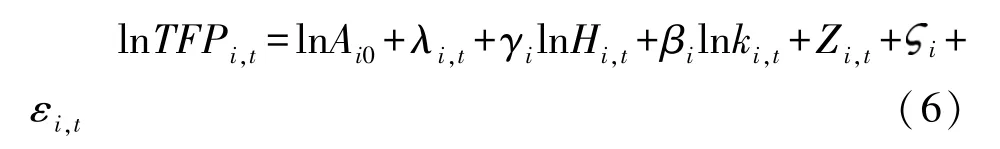
式 (6)中,全要素生产率TFP为被解释变量,人力资本集聚H和基础禀赋集聚k是本文的核心解释变量,ζ表示个体固定效应,ε表示随机干扰项,Z是可能影响全要素生产率的控制变量,包括地区开放程度、政府规模和产业结构等。
本文之所以使用TFP作为高质量发展的代理指标,是因为一般在经济体发展的初期,经济发展多依赖于要素投入,此时大量的农村剩余劳动力进入工业产业中,加上大规模的投资等行为,经济总量飞速增长。但要素驱动型的增长并不可持续,生产要素的浪费、生态环境的恶化等问题会使经济高速增长受到掣肘。因此,提高生产要素的利用率便成为当下高质量发展的核心之一。经济活动内部生产率水平的提升和要素的合理流动与有效配置是提高生产要素利用率的有效途径[35],而二者都可以通过全要素生产率反映出来。
2.3 指标的度量2.3.1 全要素生产率
TFPi,t和物质资本的测算借鉴张军和施少华(2003)[36]的计算方法, 公式如下:
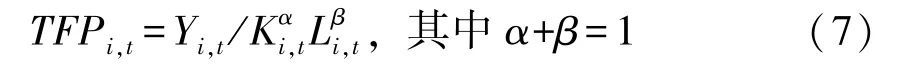
要得到全要素生产率的具体数值,必须计算出物质资本和劳动力的具体存量。参考张军等(2004)[37]的做法,利用永续盘存法计算各地级市的物质资本存量,折旧率选取9.6%,然而省级层面以下的固定资产形成总额没有公开数据。但由于固定资产投资总额和固定资本形成总额之间存在线性关系,因此,在综合考虑后,本文借鉴王艺明等 (2016)[38]的做法,利用各地级市当年的固定资产投资总额 (Total Investment in Fixed Assets,TIFA)占其所在省份当年的固定资产投资总额 (Province Total Investment in Fixed Assets,PTIFA)的比例构建固定资本系数Ri,然后利用省级的固定资本形成总额 (PGFCF)对所在地级市进行估计。其具体计算公式如下:
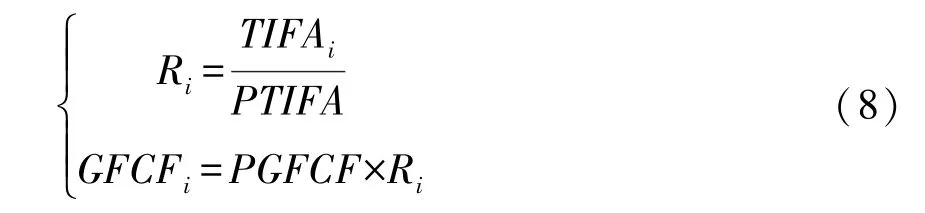
劳动力投入的测算。劳动力的投入较难识别,因此本文延续刘秉镰和李清彬 (2009)[39]的研究,采用 《中国城市统计年鉴》中年末单位从业人员数与城镇私营和个体从业人员的加总作为劳动力投入指标。
2.3.2 人力资本集聚 (H)
人力资本要素集聚指标同样由各地区平均受教育年限给出,标准的平均受教育年限的计算公式为:
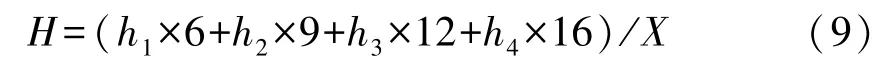
其中,h1、h2、h3、h4和X分别表示地区受小学教育总人数、受中学教育总人数、受高中教育总人数以及受大学教育总人数和地区的总人口数。但地级市层面只记录了当年各阶段学生在读人数,且高中在读人数只有2007年以后的数据,由此,受限于地级市层面数据的缺失,地区内各阶段受教育人数精确到省级层。考虑到各教育阶段在读人数与地区各阶段受教育人数存在相应的线性关系,且本文构造的是人力资本集聚变量,只需关注该变量的相对量即可。因此,本文人力资本具体的衡量方式为:
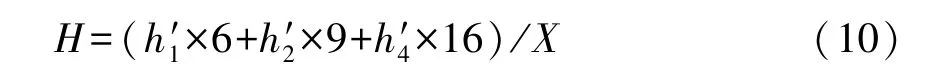
其中,h′1、h′2、h′4分别表示小学、 初中和大学阶段学生在读人数。
2.3.3 基础要素禀赋集聚 (k)
要素禀赋集聚是一个地区的基础禀赋约束,在高质量发展的背景下,要素禀赋应与该地区的发展阶段相匹配,符合比较优势的发展方式才能实现高质量发展约束下的高速发展[31],因此本文采用地区物质资本存量与劳动力要素投入的比值作为其代理变量。其计算公式为:

其中,物质资本存量K和劳动力投入L均已在前文给出。
2.3.4 控制变量的选取
地区开放水平 (open)。由于资本具有溢出效应,理论上讲,一个地区对外开放程度越高,则越容易接触到附着于资本之上的技术,考虑到地级市数据的可得性,本文选取年度利用外资额与地区生产总值的比值作为地区开放水平的代理变量。政府规模 (GOV)。政府规模对地区全要素生产率的作用比较复杂。政府可以通过提供公共基础设施,减少要素流动的摩擦力,从而提升全要素生产率;政府也可能为提升本地经济水平从而盲目吸引产业进驻,造成资源的浪费和无效率,从而降低全要素生产率。本文采用政府当年财政支出与地区生产总值之比作为政府规模的代理变量。产业结构 (IS)。对于产业结构的选取众说纷纭,分别选取第二产业占总产值的比重 (IS2)和第三产业占总产值的比重 (IS3)作为产业结构的代理变量。
2.4 数据的选取范剑勇等 (2014)认为集聚的研究层面应当较低,集聚层面太高无法准确反映出其具体的集聚情况[40]。考虑到数据的可得性,本文采用黄河流域生态经济带6个省份的83个地级市作为基本研究单位①,最终确定83个地级市,所选取的时间段为2003~2018年,数据均通过平减换算为2003年为基期的可比价格。所需数据均来自 《中国城市年鉴》和 《中国统计年鉴》。
3 实证结果3.1 基准模型回归结果3.1.1 基础模型回归
表1报告了面板模型的基准回归结果,模型1和模型2分别表示随机效应和固定效应的回归结果。同时,Hausman检验结果表明,固定效应模型对数据更有解释力,因此选择固定效应模型。
根据固定效应模型的回归结果,人力资本集聚 (H)和基础要素禀赋集聚 (k)对全要素生产率 (TFP)的提升具有显着的促进作用,二者均在5%水平上显着,这表明在样本区间范围内,基础禀赋和人力资本的聚集对高质量发展具有重要的提升作用。
控制变量中,政府规模 (GOV)对全要素生产率 (TFP)的作用在1%的水平下显着为正,肯定了地方政府对高质量发展的促进作用。政府通过提高基础设施建设水平以减小要素流动的摩擦促进区域经济高质量发展。产业结构 (IS2、IS3)对全要素生产率的作用效果都为正,且结果都非常显着。从二者的系数来看,第二产业对全要素生产率的弹性系数为0.2944,大于第三产业的系数0.1503,这表明在当前黄河流域生态经济带内第二产业仍然具有相当的发展潜力。对外开放水平 (OPEN)对全要素生产率的作用为负,这与预期相反,可能是由于FDI的技术封锁阻碍了FDI的溢出效应,同时由于其占据了一定的生产要素,阻碍了部分生产要素的流通[41]。
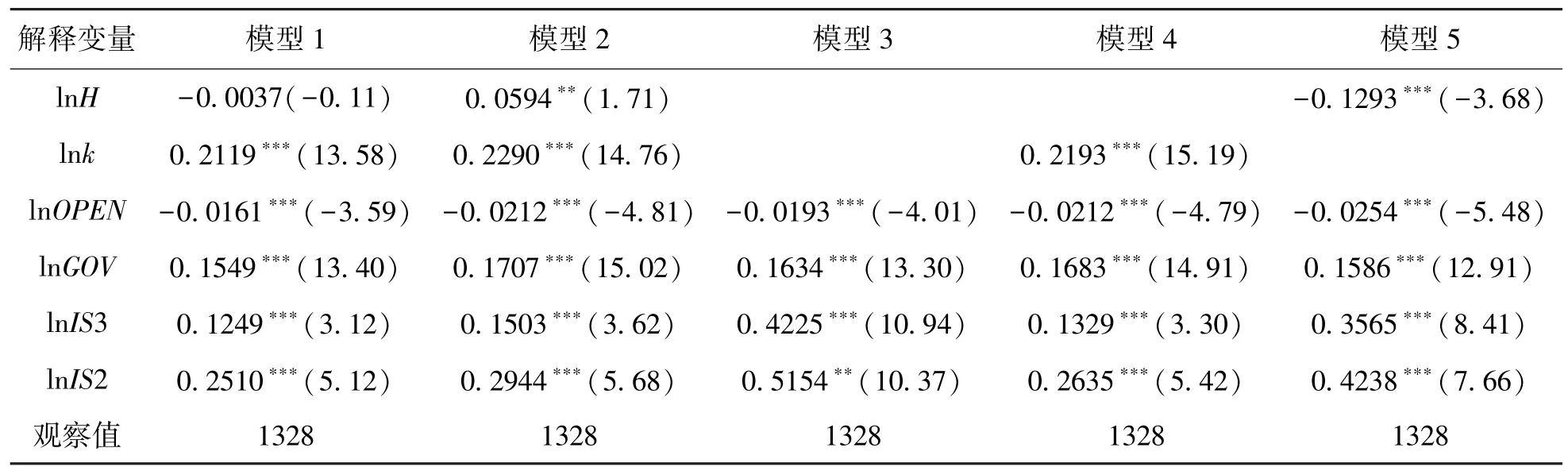
表1 基准回归结果
模型3代表了控制变量对全要素生产率的回归结果,模型4和模型5则分别代表了在控制变量的基础上加入任意一个核心解释变量的回归结果。从模型2~5回归的显示结果来看,当核心变量为只有基础要素禀赋k时,对全要素生产率的作用弹性显着为正;然而,当核心解释变量只有人力资本集聚H时,其回归结果反而变成负数,综合对比模型3~5可以发现,加入基础要素禀赋集聚后,人力资本集聚变量则变正且更加显着,由于基础要素禀赋对地区发展模式具有决定性作用[31],因此,当核心变量缺少基础要素禀赋集聚时,会出现严重的遗漏变量偏误,导致人力资本集聚对全要素生产率的作用效果并不显着。
3.1.2 集聚的异质性讨论
在表1的基准回归中显示,人力资本集聚与基础要素禀赋集聚对总体上全要素生产率表现出显着的促进作用,应该从地区和时间异质性的角度对计量模型进行重新估计。
(1)按照黄河流域的地理位置划分,将青海、甘肃、宁夏、四川、内蒙古划分为黄河上游,将山东、河南、山西和陕西归入黄河中下游,分别对两个地区进行回归,其中黄河上游共33个城市,黄河中下游共50个城市。得到核心解释变量结果如表2所示。
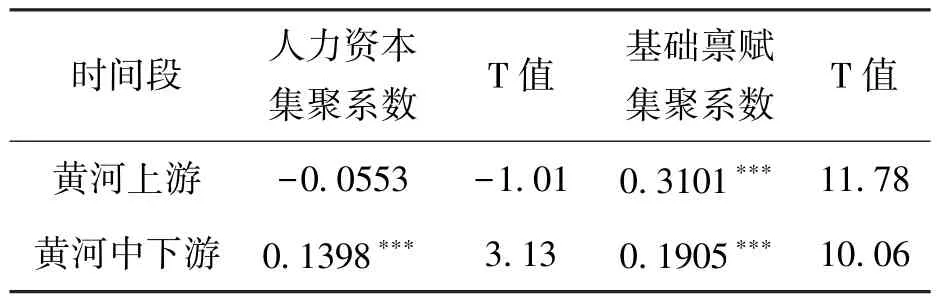
表2 分流域的主要估计结果
从表2人力资本集聚一栏来看,黄河中下游地区人力资本集聚对全要素生产率的作用效果较为显着,人力资本集聚对其全要素生产率的弹性为0.1398,相较而言,黄河上游地区人力资本集聚对全要素生产率的弹性为负,且并不显着。表明人力资本集聚对黄河中下游的作用要显着高于上游地区。从表2的基础禀赋集聚这一栏来看,黄河中下游流域和上游流域基础禀赋对全要素生产率的作用效果均在1%的水平下显着为正。在对全要素生产率的弹性大小上,黄河中上游地区的基础禀赋集聚作用于全要素生产率的系数要显着大于黄河中下游地区。基础禀赋集聚对黄河上游的效应要显着大于中下游地区。结合黄河流域经济带的实际情况,由于我国长期处于区域发展不均衡的局面[42],而黄河中下游地区所属省份多为东部和中部省份,经济发展水平很高,这些城市对基础要素投入的依赖逐渐降低,人力资本对全要素生产率的作用逐渐凸显出来。而黄河上游流域所属省份多位于我国西部地区,经济发展水平相较于东部地区稍弱,经济发展模式仍处于要素投入的阶段,基础禀赋集聚对全要素生产率的弹性非常高,但对人力资本的要求并不高,对人力资本的过分追求反而会导致地区资源的浪费,反而不利于经济的高质量发展。
(2)将黄河流域按照时间划分回归结果,同分地域估计情况类似,当按照时间划分对黄河流域生态经济带进行重新估计时,不同时间段的各个人力资本集聚系数差异很大。在人力资本方面,人力资本集聚在第1个时间段 (即2003~2010年,下同)对全要素生产率的作用系数在10%的显着水平下为负,而在第2个时间段 (即2011~2018年,下同),人力资本集聚对全要素生产率的作用系数变为0.0982,人力资本集聚对全要素生产率的作用效果变为正。这表明人力资本对经济发展的作用逐渐体现了出来。从基础禀赋集聚系数来看,两个阶段基础禀赋集聚系数对全要素生产率的作用效果皆显着为正。基础禀赋集聚系数从第1个阶段的0.3723降低至0.1997,表明整体上,黄河流域经济带对基础要素的依赖有所降低,但仍然对当前黄河流域生态经济带的高质量发展起着重要的作用。
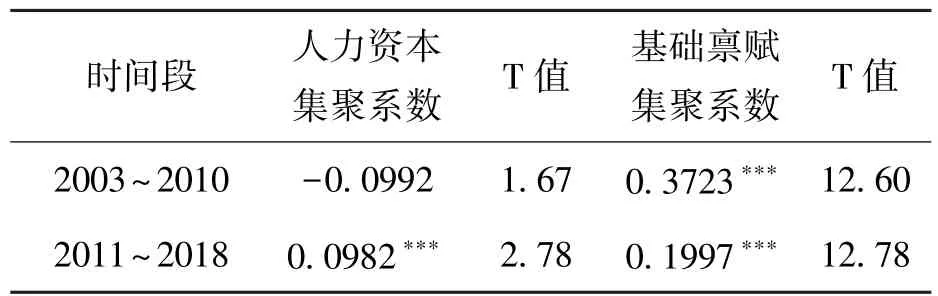
表3 分时间段回归的主要估计结果
3.2 进一步讨论近年来,越来越多的研究发现集聚具有非经济效应,随着集聚的累积,会产生集聚不经济的后果。因此在高质量发展的背景下,研究最适集聚水平对黄河流域生态经济带的发展规划具有重要的战略意义。通过上面的讨论,本文发现经济集聚呈现出显着的异质性特点,为了进一步验证黄河流域经济带的经济集聚作用效应,本文在式(6) 的基础上引入 Hansen (1999)[43]提出的面板门槛模型来衡量该效应。最终得到的面板门槛模型如下:
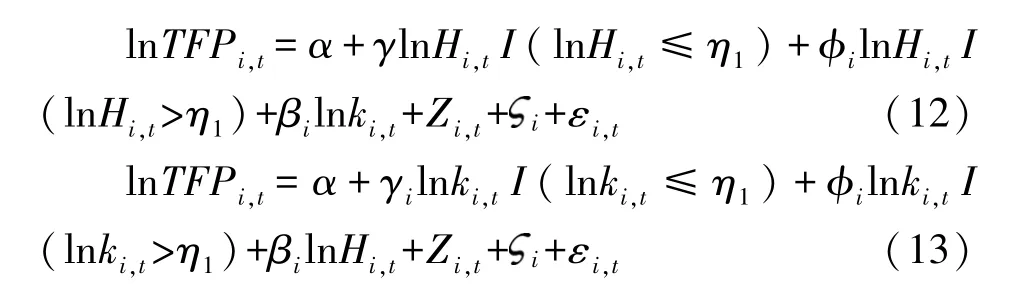
其中I(·)为示性函数,人力资本集聚为门槛变量,η为待估的门槛值。
根据上文所设定的面板门槛模型,本文首先进行门槛效应检验,将Bootstrap迭代次数设为300,Grid为400,得到的结果如表4所示,人力资本集聚通过了单一门槛的显着性检验。门槛值结果如表5所示,门槛值大小为0.7860。

表4 门槛值的显着性检验

表5 门槛值结果
表6提供了面板门槛回归模型的估计结果,可以看到人力资本对全要素生产率具有单阶门槛效应,当人力资本集聚小于0.7860时,人力资本集聚对全要素生产率的作用水平为负,但结果并不显着,当人力资本集聚水平大于0.7860时,人力资本集聚对全要素生产率的作用方式由负转正,其弹性系数为0.2854。基础禀赋集聚对全要素生产率的作用弹性为正。
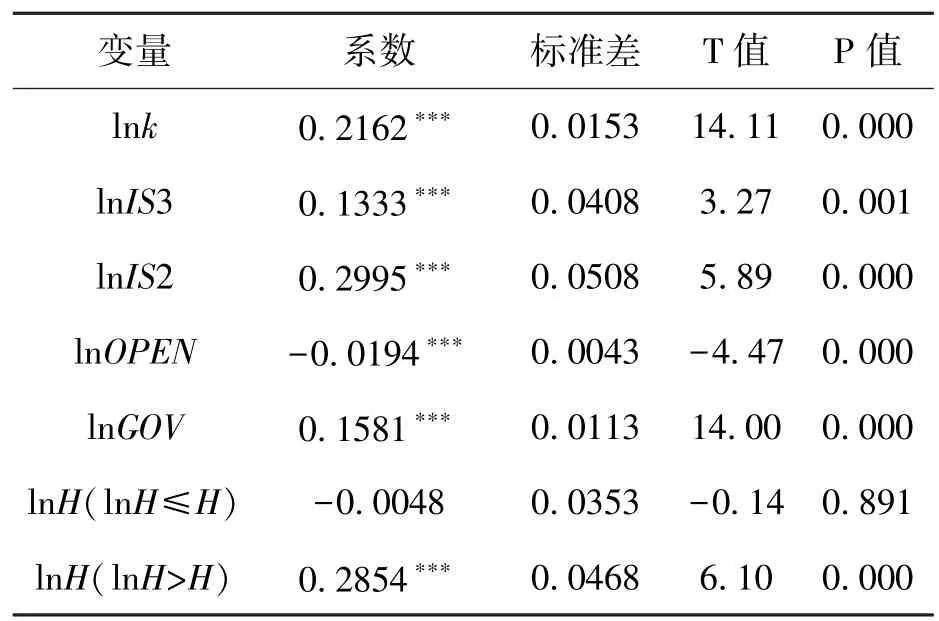
表6 面板门槛模型的估计结果
表7列举了人力资本集聚大于门槛值的部分地级市,可以发现,人力资本集聚高于门槛值的地区皆属于省会地区,其分布多位于黄河流域生态经济带的中下游地区。这是因为在一般情况下,省会城市本身就具有比其他地级市更丰富的资本要素,同时,劳动力对省会城市的偏好也促进更多人力资本在省会城市的集聚[44],更多人才的集聚加快了产业的转型升级,经济发展水平的提高又吸引了更多的要素禀赋,最终形成了发展的良性循环。
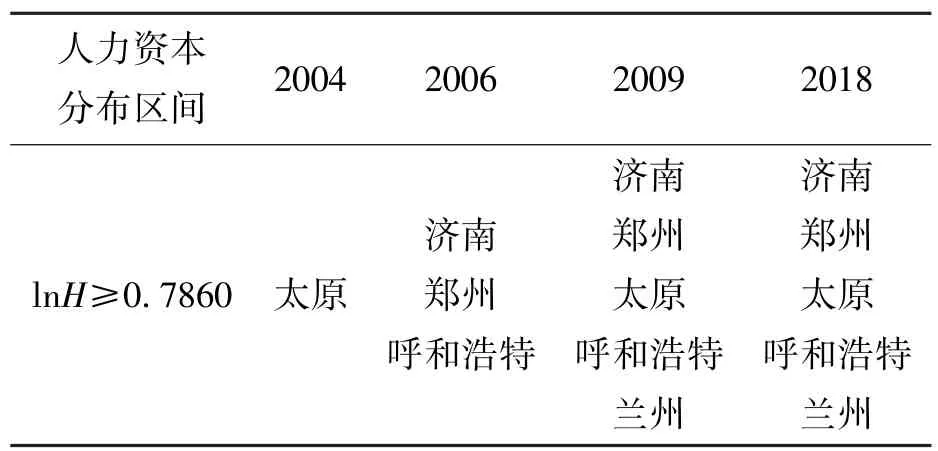
表7 部分年份黄河流域生态经济带人力资本集聚情况
4 研究结论与建议本文通过Cobb-Douglas生产函数重新构建了要素集聚对高质量发展的理论框架,并以黄河流域生态经济带2003~2018年地级市的面板数据实证分析了要素集聚对高质量发展的异质性,并最终得到以下结论:(1)总体上人力资本集聚和基础要素禀赋集聚对区域内全要素生产率具有显着的正向促进作用。要素集聚对黄河流域生态经济带高质量发展具有提升作用;(2)在不同的时间和空间上,人力资本要素集聚及基础要素禀赋集聚对全要素生产率的作用效果具有显着的异质性。具体表现为从地域来看,黄河中下游地区人力资本集聚对全要素生产率的作用弹性要高一些,黄河上游区域基础要素禀赋集聚对全要素生产率的作用效果则更高;从时间来看,人力资本集聚对全要素生产率的影响随着时间的推移由负转正。各地区应遵从自身禀赋水平,合理引导不同要素集聚,以促进黄河流域生态经济带的高质量发展;(3)人力资本集聚对全要素生产率具有一阶门槛效应,随着人力资本集聚水平跨越门槛值,人力资本集聚水平对全要素生产率的效应逐渐变为显着。同时,人力资本集聚对经济高质量发展起到促进作用的城市主要为省会城市。
中国经济正处于结构升级换挡的新常态时期,在这一背景下,黄河流域生态经济带的提出对落实高质量发展具有重要的战略意义。黄河流域横跨中国版图,长期以来我国面对着区域发展失衡问题,因此,对于实现黄河流域生态经济带的高质量发展,地区应严格按照自身的条件合理安排要素集聚,对于黄河上游地区,应以吸引基础要素禀赋集聚为主,而对于黄河中下游地区,应充分发挥人力资本集聚的比较优势。只有在适合自己自身禀赋条件下的发展才能实现资本的最快速积累,从而以最快速度提升自己的经济发展水平[31]。人力资本集聚的前提是人力资本存量的提升,而人力资本存量的提升又是一个非常缓慢的过程。因此,对于黄河中下游等人力资本相对富裕的地区,应尽可能加大人力资本投入,为高质量发展提供稳定的技术保障。而对于人力资本存量相对薄弱的黄河上游地区而言,对人力资本的投入应当适量,以避免教育资源的过度浪费、结构性失业以及人才外流问题,从而阻碍地区的高质量发展。
政府对区域内高质量发展具有相当重要的意义,它通过提供公共基础设施从而为要素集聚提供了坚实的保障。但也应处理好政府与市场的关系,以避免无序集聚情况的发生。
注释:
①部分地级市存在个别数据缺失的情况,本文采用插值法予以补全,而对于个别数据缺失严重的地级市予以舍弃,最终确定为83个地级市。