从模型、影响因素和实证误差原因看我国可转债定价研究

王予瞻，郭真华（博士生导师）

可转换公司债券（简称“可转债”）是由上市公司发行、股价达到一定条件时可以转换为发行公司普通股的一种特殊的有价证券。自1992 年11 月宝安转债成为我国第一只公募转债以来，历经试水、探索和成长等阶段，我国沪深两市可转债规模已近9000 亿元（截至2023 年8 月末）。国内可转债市场的繁荣发展有力推动了可转债定价理论的研究。当前，国内可转债定价研究主要不足表现为：一是文献主要研究内容分类不清晰，模型和参数仅做细微改动就自称创新，用很少的数据量做实证就断言有改进，缺乏与前人模型方法基于大量数据的真实效果对比，定价精度是否提升无从知晓；二是中国特色可转债制度因素、市场条件与经典理论模型适配程度不够；三是对“部分经典定价模型假定无法优化、部分客观影响因素不好度量”的难题缺乏解决办法。

对可转债定价研究而言，最重要的就是缩小计算出的理论价值与实际市场价格间的差距，差距越小，理论价值才越有现实指导和参考意义。在具体研究过程中，理论模型如同大树的主干，模型参变量如同主干上的枝条，理论价值如同花果，实证就是要找到理论价值之“花果”与市场价格之“花果”间的差异原因；修整主干和枝条有利于花果的生长，改进模型设计和影响因素的测度方法也能使估算出来的可转债的理论价值更贴近实际市场价格。理论价值与实际市场价格虽必定存在误差，但通过对误差的可能原因进行分析和针对性改进，可转债的估价精度就有望不断提高。基于此，本文拟从模型、影响因素和实证误差原因三个维度对我国可转债定价研究予以综述。

模型选择是可转债定价工作的第一步。经过前人探索，当前可用于转债定价的模型众多。这些模型分类方式大致有三种：一是依据模型中考虑的参数个数（这些参数通常包括股票价格、公司价值、利率、波动率、信用风险等），分为单因素模型、双因素模型和三因素模型；二是基于模型对主参数的选择，分为基于公司价值和基于股票价格两大类；三是根据解的表达式能否直接写出，分为可得出显式解的解析法和即便解存在也写不出显式解的数值法两大类。参考“参数个数”的方法（第一种）算不上严格意义上的分类，基于公司价值和对理论价值进行调整为可转债定价的方法（第二种）可操作性较差，而解析法和数值法（第三种）则明确对应了各种模型方法适用于定价的期权种类，应用起来十分方便。因此，本文倾向于在第三种分类方式下对可转债定价模型进行重点梳理。

为解决期权定价问题，Black 和Scholes 于20 世纪70 年代提出了著名的Black-Scholes 公式。Brennan 和Schwartz（1977）以及Ingersoll（1977）作为最早在转债定价中尝试应用B-S 期权定价模型的学者，认为可转债价值是公司市场价值与时间的函数，他们假设公司价值服从几何布朗运动，采用风险对冲和风险中性定价，运用B-S 模型推导出可转债满足的偏微分方程；再结合可转债的内嵌期权特征，利用无套利原理确定可转债的最优转换和赎回策略，由此确定偏微分方程的边界条件和终值条件；最后利用数值方法计算可转债的价值。

国内学者中，郑振龙和林海（2004）主要基于B-S模型估计各内嵌条款的价值，分析各条款对可转债整体价值的影响。张卫国等（2010）在传统B-S 定价理论中考虑股价波动、无风险利率等因素的模糊不确定性，给出具有三角模糊数形式的可转债定价公式。樊鹏英等（2014）按照“对参数方法进行非参数修正”的思路，建立Ad hoc BS 模型为可转债定价。由于所需变量易得、计算过程简便，B-S模型逐渐成为实际操作中最常用的期权定价方法。

随着研究的推进，学者们逐渐发现B-S 模型只适用于欧式期权、正股不发放股利、有效市场和市场无卖空以及股价波动遵循几何布朗运动等情境，前提假定过于严格，并做了针对性的改进尝试。此外，只能对每个期权单独定价，也是B-S 模型一个极为明显的硬伤。对于可转债这样各条款有机结合的情形，各内嵌期权定价后的简单加总无法等同于可转债的整体价值。因此严格意义上来说，B-S 只适用于无路径依赖条款和无股利发放的可转债（蒋殿春和张新，2002）。

为何有如此多缺陷的B-S 模型依然被广泛采用呢？一方面，将可转债的价值划分为债券价值和期权价值，投资者理解起来比较容易，可以较为清楚地判断可转债的下跌空间有多大、所含期权的价值是否合理。另一方面，B-S模型还是有很多适用情形，例如为初始上市的可转债定价（因为各内嵌条款只有在6个月或者更长时间之后才能实施，选择此时点就大大简化了定价过程），或为我国的分离交易可转债定价（闻岳春和邱小平，2009）。

1.二叉树模型。Cox 等（1979）基于风险中性理论和数值法建立了二叉树定价模型。该模型不仅能够通过树图直观形象地呈现股价路径信息，还能较为合理地融入无风险收益率的利率期限结构。但是，该模型有三个缺陷：一是从模型原理上，仅用两种状态来近似模拟标的变量未来的变化显得过于简单。马长福等（2019）还认为，所有叉树类模型均存在前期节点太少易引入误差、后期节点过多易导致大量冗余计算的问题。二是在模型假定中，二叉树模型需满足与B-S 模型相同的、我国市场暂不符合的有效市场假定。三是从模型实操看，为了还原现实中连续的股票价格变动情境，需要将二叉树模型拓展到n期，这样做将导致树图趋近于多条连续曲线，中间路径信息丧失，仅能观察到期日的股票终值，将不再适合含路径依赖特性的可转债内嵌期权，且当n→∞时计算复杂程度将变得相当高（龚朴等，2004）。孙卿东和朱海洋（2010）、谢百帅等（2013）提出可以改用三叉树模型以提高模型精度，但二叉树模型的上述缺陷仍未根本克服。

2.Monte Carlo 方 法 和LSM 模 型。Monte Carlo 模拟是一种基于已知概率分布的随机抽样方法，常被用于构造符合一定规则的随机数以解决数学上的各种问题。Buchan（1997）首次将Monte Carlo 模拟方法应用到可转债定价中。熊思灿和杨志辉（2008）用Monte Carlo 模拟股价运动并基于简化的AFV 模型得到了样本可转债的价格。利用Monte Carlo 模拟为可转债定价的缺陷是：它只选取了每条路径到期日的股价终值进行贴现，仅适用于欧式期权而不能为美式期权和路径依赖期权定价。基于此，Longstaff 和Schwartz（2001）提出了最小二乘蒙特卡罗模拟方法（Least Squares Monte Carlo Simulation，LSM）。

与Monte Carlo 模拟一样，LSM 也是通过计算机产生一系列的股价正态分布随机数，根据剩余期限的不同和要求精度的不同选取股价波动的步长和路径数；不同之处在于，LSM 对各路径各时点的期权利用普通OLS 从后往前仿真回归，计算其后续持有价值在当前时点条件期望值的拟合值——预期持有价值。在具体比较预期持有价值和即期执行支付的过程中，可以充分考虑各隐含期权之间、期权与债券之间价值的相互影响，作出当下应继续持有可转债还是执行各类期权的判断，直至初始时点。这样一来，可转债存续期各时点的现金流已知，通过现金流折现即可得到需要的定价时点的可转债价值。如此，LSM 不仅能发挥Monte Carlo 模拟股价路径的优势，而且弥补了其不能为美式期权和路径依赖型期权等奇异期权定价的缺点，可以更加准确地评估可转债的价格。唐文彬和张小勇（2008）还认为，LSM 能有效克服因步长太短所带来的计算量呈几何级数增加的缺陷，从而提高模型的执行效率。

针对从后往前逆推时回归方法的选用问题，部分学者认为兼具适用性广泛、定价结果准确、计算速度快等优点的LSM 方法仍有许多可以改进的地方。如张卫国等（2011）使用能同时考虑解释变量和被解释变量的TLS 回归方法，并利用方差减小技术有效降低了LSM估计结果的误差。

3.其他数值方法。有限元方法将求解范围离散成有限个连结在一起的单元，将无限连续自由度问题简化为离散的有限自由度问题，通过在每个单元内假设近似函数来分片表达求解域上的未知场函数，插值计算出各场函数的近似值，最后得到整个求解区域上的近似解。有限差分法主要是利用网格线将定解区域化为离散点集，通过构造差分格式将原来的偏微分方程定解问题化为代数方程组，通过解代数方程组得到由定解问题的解在离散点集上的近似值组成的离散解，应用插值方法便可从离散解得到定解问题在整个定解区域的近似解。龚朴等（2004）认为，有限元方法对整个求解区域进行求解，可以更容易地处理不规则的区域，能够得到精确的对冲比，能够更灵活地处理终端条件以及边界条件，较有限差分法更具优势。

可转债定价工作的第二步就是要甄别并计算影响因素。主要影响因素有以下四种：

稀释效应，是指大量可转债投资者将可转债在短时间内转换为发行公司普通股时，发行公司总利润无变化而总股本激增导致每股收益（EPS）降低，市场投资者负面情绪上升，最终致使股价走低的现象。当前对如何处理稀释效应存在两种观点：一种认为考虑稀释效应既麻烦又没有必要，因为早在可转债发行之初股票投资者就应预期到未来转股的可能，稀释效应已在开始的股价波动中被充分消化，不应再产生后续影响。另一种则坚持定价中应当考虑稀释效应，认为稀释效应会影响转股后的股东权益和股票价格，不考虑稀释效应会明显高估可转债的价值。具体而言，可基于转股仅是公司资本结构的调整、转股前后公司价值不变这一事实，求解出转股后的股价（Hull等，2022）。

此外，在可转债定价过程中还有一些与稀释效应有关的观点需要考虑。闻岳春和邱小平（2009）指出，考虑到转股时间的不确定和转股价下修的可能，可转债的稀释效应应强于股本权证的稀释效应。冯建芬等（2018）研究发现，尽管稀释效应会使可转债的价值降低，却不会影响投资者行使转股权的概率和平均时点。赵旭（2011）研究发现，股价波动率和企业价值波动率的差异会随着稀释效应的增强而变大，因此强稀释效应下不能简单地用前者代替后者。

在计算可转债的理论价值尤其是其中期权部分的价值时，除非使用Canonical 这样可直接利用标的资产的历史收益数据为期权定价的非参数方法，能够规避对波动率的估计（余喜生，2009），否则波动率几乎是必须考量的因素。根据计算方法不同，波动率分为隐含波动率和历史波动率。

1.隐含波动率。隐含波动率需要将市场上已有标的股票的期权价格代入Black-Scholes 模型，反推出标的股票的波动率数值，其计算要求具备一个相对成熟的股票期权市场，这样计算出的波动率才有参考价值。然而，我国证券市场一直没有场内个股期权，期权市场价格受过度投机影响而严重偏离理论价值的情况又时有发生，这些均使得隐含波动率的计算更加困难，常用的退而求其次的方法是用可转债中内嵌期权反推隐含波动率（倪武帆和李明生，2023）。

2.历史波动率。历史波动率依据历史股价（去除派息、送股、增发、配股等影响）估计，反映的也是股票市场的历史信息，其计算主要以标准法（Hull，2022）和Bollerslev（1986）的GARCH 模型两种方式为代表。前者假设波动率为固定值，具有计算简便的优势；后者更加符合实际股价的运动方式，能够更好地刻画金融变量的厚尾特征。

值得注意的是，可转债发行本身会对股价波动率产生影响，一般会使得股价波动率降低。因此，需要在发行之前的历史波动率基础上，综合分析可转债发行对波动率的可能影响及平均幅度，并做出相应的调整（廖萍康等，2012）。

对于可转债定价模型是否要考虑信用风险存在两种观点：郑振龙和林海（2004）、闻岳春和邱小平（2009）认为我国的信用风险溢酬不高，可转债的信用风险可以忽略；而王新哲和周荣喜（2006）则认为，既然可转债是公司债券，那么信用风险的考量就十分必要。

作为最常见的信用风险表现形式，信用风险溢价被广泛讨论。如郑振龙和林海（2003）采用样条函数法估计公司债券收益率期限结构，再减去同一时期的市场利率水平，即为公司的违约风险溢酬；直接利用企业债风险利率折现也未尝不可，但所选企业债要与样本可转债评级相同、剩余期限相近，若发行公司有满足条件的普通债券则更加合适。程志富和胡昌生（2020）则是假设公司信用风险溢价遵循一个Guass-Wiener 增量过程，将其加入构建的交换期权模型中，计算出可转债的无套利价格。

信用风险溢价并非可转债违约风险的唯一表现形式。如岳喜伟等（2006）、谢百帅等（2013）、王力（2018）分别在二叉树定价模型中引入可转债转股概率、违约强度、发行人破产率，帮助判断每个股价路径节点是否转股；宋殿宇等（2011）、乔高秀和潘席龙（2013）分别采用信用监控模型（KMV）、Ayache 违约风险简化模型考虑了跳扩散过程下可转债的违约风险；马长福等（2019）以可转债违约概率与回收率的乘积度量投资者的违约风险损失；常竞文和王永茂（2020）认为转债的瞬时违约风险遵循泊松过程，并以此求出违约前后组合价值的变化。

已有研究普遍认为，违约风险会拉低可转债的理论价值和实际市场价格。如王乐乐和边保军（2010）、杨立洪等（2010）发现仅当违约强度趋近于0 时，具有信用风险的可转债价格才趋向于无信用风险的可转债价格；刘郁和田乐蒙（2021）研究发现，倘若发行人被市场认为具有实际违约风险、有降级风险或出现影响较大的负面事件，可转债甚至存在跌破债底的可能。

无风险利率取值方法主要分为三类：第一类是设定无风险利率为常数；第二类会尽量选择违约风险小、流通性强、市场化程度高、不存在市场分割的利率，如国债到期收益率、银行定期存款利率、上海银行间同业拆借利率等；第三类则是估算利率期限结构，并从中选取所需期限的利率值。此外，蒋殿春和张新（2002）和岳喜伟等（2006）认为，利率的选取还受可转债能否转股的影响。不同的是蒋殿春和张新（2002）认为若能转股则取短端利率，不能转股则取长端利率，不确定时应用二者加权值贴现；岳喜伟等（2006）却觉得，若能转股则用无风险利率贴现，不能转股则需用与转债评级相同的债券风险利率贴现，不确定时要用转股概率作为权重对二者加权贴现。

可转债定价工作的第三步就是要计算理论价值之“花果”与实际市场价格之“花果”间的误差，分析误差原因并据此做出后续改进安排。从现有研究来看，误差原因主要包括主观、客观以及其他三个方面。

基于影响因素的角度，实证误差原因的主要主观原因包括稀释效应、波动率、信用风险和红利等。如在稀释效应方面，王新军和张双（2009）认为，考虑稀释效应后的可转债理论价值误差显著减小。在波动率方面，使用隐含波动率往往较历史波动率更能降低定价误差，不同金融产品、不同影响因素波动率间的相关关系也应纳入定价考量范畴。在信用风险方面，采用利率期限结构优于采用特定利率，考虑信用风险优于不考虑信用风险。在红利方面，发行时若无红利支付转股价修正规定，有必要在模型中加入对红利影响的单独处理（谢百帅等，2013）。

从市场角度看，实证误差原因主要跟市场完善程度、制度规定等因素相关。一是市场的完善程度。早期可转债市场规模小、资金少、流动性差，投资者主要是散户，股市监管缺失等均导致可转债价格被低估；股票市场不够有效，也使可转债的市场价格不能客观反映其实际价值。二是市场交易规则的限制。吴小瑾等（2005）、王静和王敏（2008）分别从无套利机会获取和对股市波动性的影响角度分析了卖空限制导致低估的原因。三是独特的制度规定。如李汉军等（2014）通过多元回归侧面证实，随着股权分置改革的推进和流通A 股比例的提高，更加有效的市场在价格中能够更加充分地体现可转债的内在价值，可转债的折价幅度也大大降低。

从投资者角度看，实证误差原因主要跟投资预期、知识储备、市场教育等因素相关。如王静和王敏（2008）认为可转债的市场价格主要由投资者行为主导，投资者行为由预期指导，而预期往往受到宏观经济环境、金融环境、市场环境及个人因素共同影响，最终又会影响对可转债价格的精确度量。

从发行公司角度看，实证误差原因主要跟发行决策相关。如郑振龙和林海（2004）认为，发行公司的主要问题在于其决策并不可控，发行公司推迟赎回时间或降低回售价格幅度过大，就会导致“公司最优决策”模型假设不成立，进一步导致可转债理论价值上升（在原本低估的基础上更加低估）。刘亮（2008）融合委托代理理论发现，公司的代理成本越高、产出水平越低时，可转债的低估程度越小，使得误差减小。

其他客观原因主要聚焦在三个方面，即样本区间正股表现、可转债是否已进入转股期以及可转债存续期限均会影响实证结果。以正股表现为例，李汉军等（2014）发现可转债的折价现象较溢价更为普遍，多元回归结果显示折价幅度与（股价/转股价）2正相关，说明我国资本市场中可转债的发行可能确实与增发新股类似。王茵田和文志瑛（2018）针对溢价现象仅在“牛市”出现，认为股票市场的繁荣会拉升对可转债的需求，提升可转债的市场价格，导致本就高估的定价误差进一步提升。岳喜伟等（2006）认为，股市表现不佳时，可转债价格会因内嵌期权价值被低估而下降。赖其男等（2005）却认为，股市表现不佳时，因投资者转向固定收益类投资产品，可转债市场价格恰恰可能上浮。刘亮（2008）与Carayannopoulos（1996）指出，可转债的低估程度在可转债处于极度虚值和极度实值时较小，随着可转债的股性增强，低估程度并非线性增加，而是呈现先增大后减小的抛物线状（与期权定价中的“期权微笑”现象相似），且Carayannopoulos（1996）发现低估程度最严重也并非发生在可转债双平状态时。上述研究具体观点总结如表1所示：

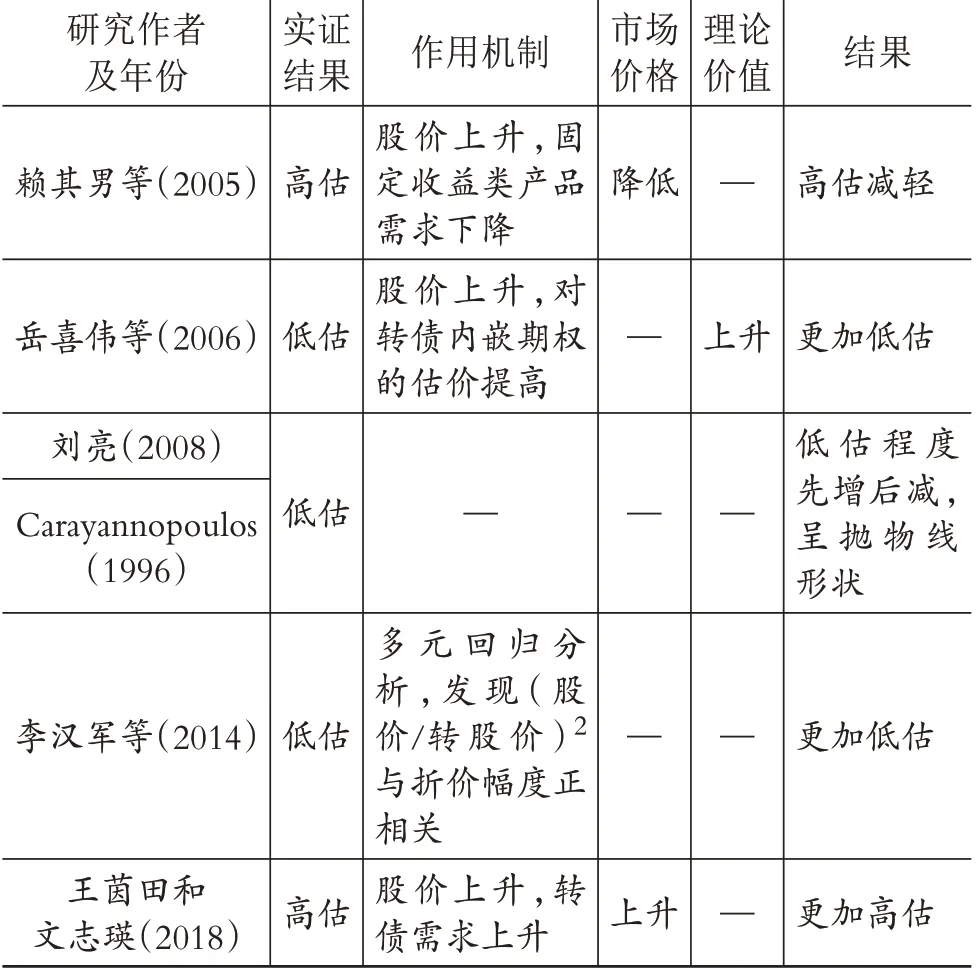
表1 关于正股表现的部分研究成果

其一，一些学者认为他们省略计算的一些要件可能影响理论结果的准确性。例如：程志富等（2013）在研究中忽略了下修条款；吴小瑾等（2005）为简化模型及求解过程，未考虑除转股条款外的其他条款，也未考虑公司发放股利的情形。其二，有的研究会出现模型前提假定与现实情况不符的状况。如吴小瑾等（2005）在根据股价波动率推导公司价值波动率时，假定发行公司除可转债外无其他债务，这种理想化假定在现实中不太可能实现，用基于该假定测算出的波动率计算可转债理论价值，自然也会产生一定程度的误差。

需要说明的是，限于篇幅，文章对部分内容进行了删减，留存备索。

可转债定价研究的重点在于理论模型、影响因素以及实证误差原因分析，从工作流程角度，三者渐次展开；从逻辑角度，三者则是“树干”“枝叶”和“对果树种植效益评价”的关系。

就模型而言，综合考虑定价公式表达的直观性和用以定价期权的复杂程度，在解析法和数值法二者间进行模型类别选择，具体选用什么模型要看对于该模型的缺陷能否接受或做出改进。但无论是B-S 期权定价模型、二叉树模型，还是Monte Carlo 方法和LSM 模型等，均面临中国特定可转债制度下赎回、回售、下修条款差异化处理的问题。

就影响因素而言，稀释效应、波动率、信用风险和贴现率等是当前研究文献讨论的重点主观影响因素（之所以成为重点影响因素，主要基于上述因素易度量并能极大限度地帮助提升理论模型的定价效果），需在众多度量方式中选择合适的方式进行计算。投资者预期、发行公司决策、市场完善程度与交易规则限制等客观因素因无法度量，其影响需要借助数学、金融知识和计算工具进行分析预测。

就实证误差原因分析而言，当前可转债定价误差分析主要聚焦于对理论模型前提假定合理性的质疑、对主观影响因素度量方式优劣的争论、对客观影响因素度量的困难以及对市场行情及产品状态的欠缺关注等方面。

如何让今后的可转债定价研究推陈出新呢？针对当前国内可转债定价研究的主要不足，笔者认为可从以下几个方面加以改进：

针对当前可转债定价研究文献主要内容分类不清晰、同类内容各说各话等问题，本文已按照理论模型、影响因素以及实证误差原因分析等可转债定价的环节进行重点梳理。这可为今后可转债券定价研究和论述提供依托和基础，同类内容兜圈子、对模型和参数仅做细微改动就自称创新的现象可能不再出现。

针对中国特色可转债制度因素、市场条件与经典理论模型适配程度不够的问题，后续可转债定价研究应立足时代背景，充分考虑我国可转债投资者结构、发行公司结构（包括信用评级、行业、资本市场层级等）以及市场制度等影响因素。应进一步打开思路，尝试脱离经典范式的局限，以开拓性的眼光思考是否有“新”可为，不断优化模型方法设定，提高定价精度，提升可转债研究对实务的指导价值，努力回应发行公司、投资者和监管部门对筹资成本、投资价值与系统性风险防控的关切。

针对现有研究对“部分经典定价模型假定无法优化、部分客观影响因素不好度量”的困难办法不多的问题，应适当放宽可转债定价模型假设，借助先进计算工具，允许“黑箱”定价，在积累可转债定价实务经验的基础上，再寻求理论的改进和突破。

【 主要参考文献】

常竞文，王永茂.随机利率模型下基于Tsallis熵分布的可转债定价［J］.运筹与管理，2020（7）：189 ～197.

程志富，胡昌生.杠杆交易限制下可转债的交换期权定价模型［J］.管理工程学报，2020（1）：195 ～199.

程志富，林勇，李巍.中国可转债的美式交换期权定价与实证研究——基于非线性最小二乘蒙特卡洛模拟方法（NLS-MC）［J］.武汉金融，2013（1）：30 ～33.

樊鹏英，吴武清，李楠等.稀释效应、非参数修正和中国股本权证的定价［J］.数理统计与管理，2014（2）：371 ～380.

冯建芬，周轩宇，段梦菲.可转债期权条款设计与影响分析［J］.管理评论，2018（8）：58 ～68.

龚朴，赵海滨，司继文.可转换债券定价的有限元方法［J］.数量经济技术经济研究，2004（2）：104 ～110.

蒋殿春，张新.可转换公司债定价问题研究［J］.国际金融研究，2002（4）：16～22.

赖其男，姚长辉，王志诚.关于我国可转换债券定价的实证研究［J］.金融研究，2005（9）：105 ～121.

李汉军，罗长林，马书博.中国可转债折价成因分析［J］.中央财经大学学报.2014（2）：44 ～50.

廖萍康，张卫国，谢百帅等.含股权稀释效应和债务杠杆作用的可转债定价［J］.系统工程，2012（6）：59 ～64.

刘亮.可转换债券市场异常现象的理论研究——基于委托代理问题的资产定价模型［J］.中国管理科学，2008（2）：14 ～19.

刘郁，田乐蒙.中国可转债投资手册［M］.北京：中国经济出版社，2021.

马长福，许威，袁先智.基于双因子柳树的中国可转换债券定价研究［J］.系统工程理论与实践，2019（12）：3011 ～3023.

倪武帆，李明生.可转换债券隐含波动率测度及其内在价值评估——以上市商业银行可转换债券为例［J/OL］.价格理论与实践：1 ～4［2023-10-11］.http：//kns.cnki.net/kcms/detail/11.1010.F.20230707.0845.002.html.

乔高秀，潘席龙.跳扩散模型下考虑不同违约回收率的可转债定价［J］.系统工程，2013（3）：1 ～7.

宋殿宇，金华，刘善存.双指数跳扩散过程下带违约风险的可转债定价［J］.系统工程，2011（6）：60 ～64.

孙卿东，朱海洋.三叉树模型在可转债定价中的应用［J］.科学技术与工程，2010（9）：2267 ～2270.

唐文彬，张小勇.LSM 可转债定价模型及其应用研究［J］.财经理论与实践，2008（4）：50 ～53.

王静，王敏.基于集对论的可转换债券定价模型［J］.商业研究，2008（4）：1～8.

王乐乐，边保军.约化框架下带有信用风险的永久可转债定价［J］.同济大学学报：自然科学版，2010（6）：935 ～940.

王力.巨灾可转换债券的定价模型研究［J］.保险研究，2018（6）：56 ～65.

王新军，张双.基于蒙特卡罗方法的权证定价［J］.统计与决策，2009（24）：128 ～130.

王新哲，周荣喜.基于利率期限结构模型的中国可转换债券定价分析［J］.管理科学，2006（2）：78 ～82.

王茵田，文志瑛.向下修正条款对中国可转债定价的影响［J］.清华大学学报：自然科学版，2018（1）：108 ～112.

闻岳春，邱小平.我国可转债定价模型探讨［J］.商业经济与管理，2009（8）：63 ～70.

吴小瑾，陈晓红，张泽京.基于公司价值的可转债定价实证研究［J］.系统工程，2005（10）：29 ～33.

谢百帅，张卫国，廖萍康等.基于三叉树模型带信用风险的可转债定价［J］.系统工程，2013（9）：18 ～23.

熊思灿，杨志辉.可转债的定价模型及数值解法［J］.统计与决策，2008（21）：42 ～44.

杨立洪，蓝雁书，曹显兵.一般Levy过程下带违约风险的可转换债券定价模型［J］.系统工程理论与实践，2010（12）：2184 ～2189.

余喜生.一种新非参数方法在可转债定价中的应用［J］.统计与决策，2009（19）：150 ～151.

岳喜伟，张永任，赵海焰.可转债定价的二叉树法［J］.统计与决策，2006（3）：124 ～125.

张卫国，史庆盛，肖炜麟.中国可转债模糊定价及其算法研究［J］.系统工程学报，2010（2）：241 ～245.

张卫国，史庆盛，许文坤.基于全最小二乘拟蒙特卡罗方法的可转债定价研究［J］.管理科学，2011（1）：82 ～89.

赵旭.分数布朗运动下B-S 权证定价模型的修正［J］.统计与信息论坛，2011（2）：12 ～19.

郑振龙，林海.中国可转换债券定价研究［J］.厦门大学学报（哲学社会科学版），2004（2）：93 ～99.

郑振龙，林海.中国违约风险溢酬研究［J］.证券市场导报，2003（6）：41 ～44.

Bollerslev T..Generalized autoregressive conditional heteroskedasticity［J］.Journal of Econometrics，1986（3）：307 ～327.

Brennan M.J.，Schwartz E.S..Convertible bonds：Valuation and optimal strategies for call and conversion［J］.The Journal of Finance，1977（5）：1699 ～1715.

Buchan M.J..Convertible bond pricing：Theory and evidence［M］.Cambridge：Harvard University Press，1997.

Carayannopoulos P..Valuing convertible bonds under the assumption of stochastic interest rates：An empirical investigation［J］.Quarterly Journal of Business and Economics，1996（3）：17 ～31.

Cox J.C.，Ross S.A.，Rubinstein M..Option pricing：A simplified approach［J］.Journal of Financial Economics，1979（3）：229 ～263.

Hull J.C..Options，futures，and other derivatives（Eleventh edition）［M］.New York：Pearson Education Inc.，2022.

Ingersoll J.E..A contingent-claims valuation of convertible securities［J］.Journal of Financial Economics，1977（3）：289 ～321.

Longstaff F.A.，Schwartz E.S..Valuing American options by simulation：Asimple least-squares approach［J］.The Review of Financial Studies，2001（1）：113 ～147.