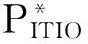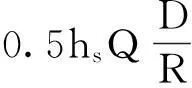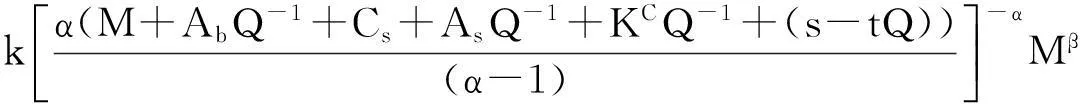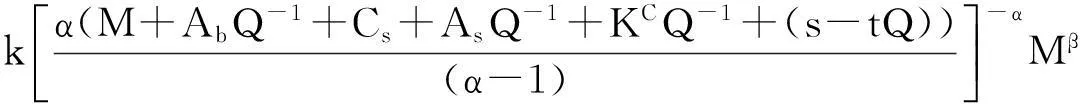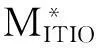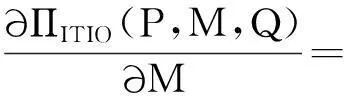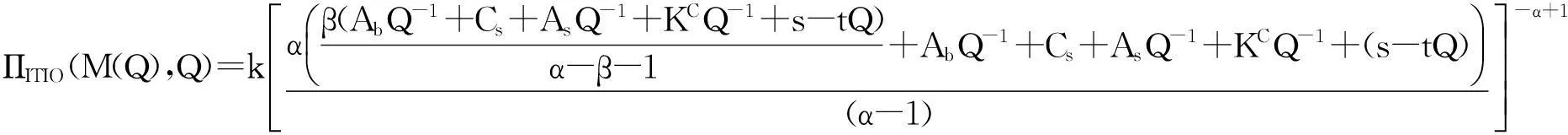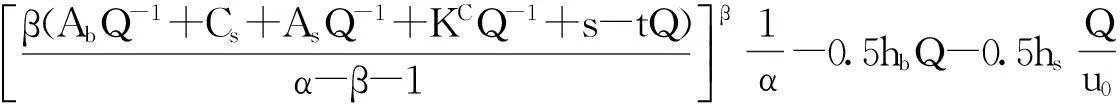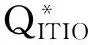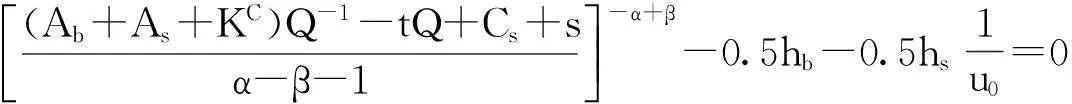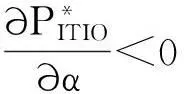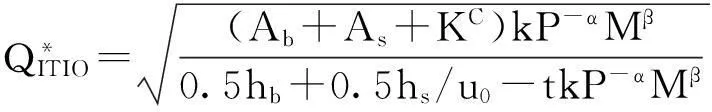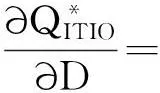考虑营销成本的库存与运输联合优化三阶段决策模型研究

李富昌

(云南师范大学，昆明　650500)



考虑营销成本的库存与运输联合优化三阶段决策模型研究

李富昌

(云南师范大学，昆明650500)

摘要〔〕一般来说，个体最优和整体最优是不一致的，二者之间存在着偏差，这一偏差就是分散优化带来的效率损失。库存与运输联合优化(ITIO)将物流系统中的库存控制和运输管理融合到一个大问题中，去寻求这一联合问题而非单个问题的最优解决方案，可以最优化整个配送系统的运营成本。本文在考虑营销成本条件下，建立ITIO三阶段决策模型，并求解分析模型性质。研究表明：ITIO零售价和营销成本与需求的营销成本弹性、零售商订购成本、供应商生产启动成本、供应商生产成本、运输固定成本和运输可变成本正相关；与需求函数的价格弹性和订货批量负相关；当订购数量相同时，零售商单独优化的营销成本大于ITIO联合优化的营销成本。

关键词〔〕营销成本库存运输联合优化零售商供应商

前言

自从Harris(1913)对供应链整合的开创性研究以来，有许多学者对不同类型供应链的物流成本整合优化模型进行了研究[1]。其中把库存成本和运输成本整合起来的研究最受瞩目，这一研究的目的在于寻找最小化库存和运输总成本的运输策略。这是一个非常有趣且有现实意义的问题，因为降低运输成本的时候，会导致库存成本增加，而降低库存成本的候也会导致运输成本增加，运输成本和库存成本存在着彼此消减的关系。对这类库存运输整合优化的早期研究，Bramel和Simchi-Levi(1997)和Campbell等(1998)进行了综述[2，3]。在之后的研究中，Bard等(1998)构建了求解库存运输联合优化问题的分解算法，把求解方法分解成两个步骤：第一步确定需要访问的客户；第二步确定供应商给该客户配送的最佳策略[4]。Berman和Larson(2001)使用随机动态规划方法研究了库存运输优化问题，求出其配送策略[5]。Jaillet等(2002)设计了增量成本近似估计用于求解最小年库存配送期望成本[6]。Bertazzi等(2002)，Campbell和Savelsbergh(2004)的研究表明，同时考虑库存控制和运输决策可以极大地降低物流系统成本[7，8]。Gaur和Fisher(2004)研究了Albert Heijn超市供应链库存和运输联合优化问题，他们的研究假设由零售商也就是超市拥有供应链网络，模型结论在Albert Heijn超市的应用证明了把库存成本和运输成本整合到一个系统中进行最小化，可以让企业取得很大的竞争优势[9]。Bertazzi(2008)研究了一对多配送系统中，多产品无限周期库存运输联合优化问题，并分析了直接配送策略的绩效影响[10]。Chen和Lin(2009)建立了基于对冲和随机需求的库存运输联合优化模型，研究了有限运输能力和时间约束下的多产品、多周期补货策略问题。他们的研究达到了3个目标：第一是使用GARCH模型预测来最小化需求波动；第二是在最大化每个消费者长期净现值基础上找出最优的短期多产品补货策略；第三是最小化库存和运输成本[11]。国内也有部分学者对库存运输联合优化进行了研究，叶志坚等(2003)讨论了VMI模式下供应商自身库存补充和配送的整合优化问题，通过构建(0，Q)库存补充策略，使长期期望平均运作总成本最小的优化模型来确定系统最佳库存补充量和配送周期[12]。李富昌(2012)采用讨价还价框架研究了零售商和供应商库存运输联合优化(ITIO)利润分配问题[13]。肖继先等(2013)根据最大最小运送周期定义，建立最大最小运送周期库存与运输模型以降低两级供应链成本[14]。葛显龙等(2014)利用改进的云遗传算法对库存与运输整合优化模型进行求解[16]。

这些研究没有研究需求函数的具体形态，只是假设需求函数为确定性需求和随机需求，然后建立模型，设计相应算法对模型进行求解。本文假定需求函数为零售价格和营销成本的函数，并且考虑运输能力柔性对运输成本的影响，建立两级供应链系统库存运输联合优化模型，并对模型进行求解。本文的另一个创新之处在于决策变量有多个，一般库存运输联合优化研究都是研究单决策变量的，而本文选取零售价、订货批量和营销成本3个变量作为决策变量。

1模型描述

1.1模型假设

假设供应链系统由一个供应商和零售商组成，供应商生产成品，决定零售商的配送批量，然后给零售商送货，零售商收到供应商配送的商品后，需要花费一定的营销成本用于产品的销售。供应商在正式生产之前，需要花费一定的生产准备成本，用于调整机器、培训员工和整理原材料。供应商在给零售商配货时，需要花费固定运输费用和可变运输费用，固定运输费用与运输数量无关，仅与配送次数有关。比如车辆启动费，司机的工资费用都可以纳入固定运输费用范畴。市场需求是商品零售价和营销成本的函数，设α和β分别为需求价格弹性和需求营销成本弹性，零售商可以通过α和β了解市场需求。不允许缺货，因此要求生产率大于或等于市场需求率，我们假定生产率和市场需求率的关系由下式线性决定。

R=u0D(P，M)，u0≥1

(1)

其中R为生产率，D为需求率，P为零售价，M市场营销费用，u0表示生产安全系数。

为了模型分析更为简便，我们假定供应商和零售商的订货批量是一样的，即供应商决定的订货批量就是零售商接受的订货批量。

1.2决策变量

Q为零售商订货批量

P为零售商的零售价

M为零售商市场营销成本

1.3输入变量

V为供应商给零售商的批发价

k为需求函数系数(k>0)

u0为生产函数系数(u0≥1)

hb为零售商单位商品库存成本

hs为供应商单位商品库存成本

α为需求的价格弹性，其中α>1

β为需求的营销成本弹性，满足0<β<1，β+1<α

Ab为零售商订购成本(￥/每次订购)

As为供应商生产启动成本(￥/每次启动)

Cs为供应商生产成本，包括材料和零部件等采购成本(￥/每单位产品)

R为供应商生产率(/单位时间)

D(P，M)为市场需求率(/单位时间)，与Lee和Kim(1993)一样[17]，我们假设

D(P，M)=kP-αMβ

(2)

其中，P为零售商向消费者销售产品的价格，M为零售商市场营销成本。

KC为运输固定成本

n=s-tQ为运输可变成本，其中s和t为大于零的系数，t越小，表示供应商运输能力柔性越强。

1.4供应商和零售商利润函数

1.4.1零售商利润函数

本文的模型是建立在Esmaeili等(2009)基础之上的，他们的研究假定库存持有成本是产品价值的线性函数，用一个比率i(0

此外他们的研究忽略了运输成本，事实上运输成本是产品总成本的一个重要组成部分，尤其在一些生鲜果蔬类产品中，运输成本和库存成本占了产品成本的主要部分。产品的运输成本分为两个部分，第一部分是固定运输成本，比如车辆启动费、发车费、维护保养费等成本，这部分成本与产品的数量无关，在我们的研究中用KC表示。另一类是可变运输成本，这部分成本与产品的运输数量相关，我们假定单位运输可变成本与运输数量的关系为n=s-tQ，其中n为单位运输可变成本，Q为运输数量(批量)，s、t为大于零的系数。

由以上分析可知，零售商的利润可以表示如下：零售商的的利润函数=产品销售收入-产品购买成本-营销成本-订货成本-库存成本，或用数学符号表示为：

(3)

1.4.2供应商收益函数

我们接着分析供应商的利润函数和最优策略，供应商的利润函数由以下基本部分组成，它们之间的关系为：供应商利润=销售收入-生产成本-生产准备成本-库存成本-运输成本(运输可变成本+运输固定成本)，把相应的数学表达式代入，供应商利润可以表示为：

(4)

2ITIO整合优化模型

前一部分建立了供应商和零售商的利润函数，以这些利润函数为基础，得出自己的最优决策。但是这只是双方各自的个体最优策略。一般来说，个体最优和整体最优是不一致的，他们之间存在着一个偏差，这一偏差就是分散优化带来的效率损失。为了克服这种效率损失，达到全局最优，我们引入整合供应商和零售商的库存运输联合优化模型。

我们把整个供应链看成一个系统，站在整个系统的角度来进行决策，假设有一个决策中心负责整个供应链的运作，那么这一决策中心的利润函数可以表示为：库存运输联合优化利润=销售收入-营销成本-订购成本-零售商库存成本-生产成本-生产准备成本-供应商库存成本-运输可变成本-运输固定成本，把相应的表达式代入，可以得到ITIO联合优化利润函数：

把需求函数D(P，M)=kP-αMβ代入上式，可化为：

(5)

(6)

由一阶条件，可以求解出：

(7)

对(5)进行整理，可变形为：

将(7)式代入(5)式，可将(5)式化为：

化简为：

(8)

(9)

将P*代入上式，可以求出：

(10)

将(10)式代入(7)式，可以把P*化简为：

(11)

决策中心利润函数可以化为：

将(10)式代入(8)时，决策中心利润函数变为：

(12)

化简为：

(13)

3ITIO结论分析

由前面部分对两级供应链系统库存运输联合优化的分析，我们可以得到如下一些结论。

命题1：库存运输联合优化的产品零售价格与需求的营销成本弹性、零售商订购成本、供应商生产启动成本、供应商生产成本、运输固定成本和运输可变成本正相关；与需求函数的价格弹性和订货批量负相关。

证明：命题结论比较明显，只有需求函数的价格弹性影响不太明显，因此我们着重研究需求价格弹性的影响。

命题2：库存运输联合优化的产品营销成本与需求的营销成本弹性、零售商订购成本、供应商生产启动成本、供应商生产成本、运输固定成本和运输可变成本正相关；与需求函数的价格弹性和订货批量负相关。

证明：因为其他参数的影响较为明显，我们仅分析β的影响。

命题3：库存运输联合优化的最优订货批量与零售商订购成本、供应商生产启动成本、运输固定成本和需求量正相关；与供应商单位库存成本、零售商单位库存成本和运输能力柔性负相关。

证明：将决策中心利润函数对Q求导：

求解得到：

命题4：当订购数量相同时，零售商单独优化的营销成本大于ITIO联合优化的营销成本。也就是说，联合优化可以节约零售商的营销成本。

4结论

在本文中，我们考虑了由供应商和零售商组成的两级供应链优化问题。供应商生产产品，并将产品销售给零售商，零售商再把产品销售给消费者。我们假定供应商的生产率是市场需求率的线性函数，并且我们把营销成本引入需求率当中，假设需求率是价格和营销成本的函数。

在库存运输联合优化模型中，决策中心联合作出订货量、零售价和营销成本决策。然后给出了库存运输联合优化最优策略的求解方法，并对模型进行了分析。

研究表明：库存运输联合优化的产品零售价格和营销成本与需求的营销成本弹性、零售商订购成本、供应商生产启动成本、供应商生产成本、运输固定成本和运输可变成本正相关；与需求函数的价格弹性和订货批量负相关；订货批量与零售商订购成本、供应商生产启动成本、运输固定成本和需求量正相关，与供应商单位库存成本，零售商单位库存成本和运输能力柔性负相关；当订购数量相同时，零售商单独优化的营销成本大于ITIO联合优化的营销成本。

参考文献

[1]Harris,F.W..How Many Parts to Make at Once[J].Factory,The Magazine of Management,1913，10(2)：135～136.Reprinted in Oper.Res,1990,38(6):947～950

[2]Bramel,J.,D.Simchi-Levi.The Logic of Logistics[M].Springer,New York,1997

[3]Campbell,A.M.,L.Clarke,A.Kleywegt,M.W.P.Savelsbergh.The Inventory Routing Problem[M].T.G.Crainic,G.Laporte,eds.Fleet Management and Logistics.Kluwer,Boston,1998：95～113

[4]Bard,J.,L.Huang,P.Jaillet,M.Dror.A Decomposition Approach to the Inventory Routing Problem with Satellite Facilities[J].Transportation Science，1998a，32：189～203

[5]Oded Berman·Richard C.Larson.Deliveries in an Inventory/Routing Problem Using Stochastic Dynamic Programming[J].Transportation Science，2001，35(2):192～213

[6]Patrick Jaillet·Jonathan F.Bard·Liu Huang·Moshe Dror.Delivery Cost Approximations for Inventory Routing Problems in a Rolling Horizon Framework[J].Transportation Science，2002，36(3):292～300

[7]Bertazzi,L.,Paletta,G.,Grazia,S.M..Deterministic Order up to Level Policies in an Inventory Routing Problem[J].Transportation Science,2002,36(11):119～132

[8]Campbell,A.,Savelsbergh,M.A Decomposition Approach for the Inventory-routing Problem[J].Transportation Science,2004b,38(4)：488～502

[9]V Gaur,M L.Fisher.A Periodic Inventory Routing Problem at a Supermarket Chain[J].Operations Research,2004,52(6):813～822

[10]Luca Bertazzi.Analysis of Direct Shipping Policies in an Inventory-Routing Problem with Discrete Shipping Times[J].Management Science,2008,54(4):748～762

[11]YM Chen,CT Lin.A Coordinated Approach to Hedge the Risks in Stochastic Inventory-routing Problem[J].Computers & Industrial Engineering,2009,56(3):1095～1112

[12]叶志坚，杜文，王清荣，等.供应商管理库存系统中库存和运输计划整合[J].交通运输系统工程与信息，2003,3(4):82～88

[13]李富昌.库存与运输联合优化利润分配研究[J].工业技术经济，2012，(11)：97～103

[14]肖继先，康玉茜，孔闪闪.最大最小运送周期下的库存与运输优化模型[J].辽宁工程技术大学学报(自然科学版)，2013，32(3):393～396

[15]李五四，张伟亮．构建反映和满足消费者需求的网络营销物流组合优化模型[J]．工业技术经济，2013，(5)：3～9

[16]葛显龙，辜羽洁，王伟鑫.供应链环境下的库存与运输整合优化模型及算法[J].系统工程，2014，32(1):26～32

[17]Lee,W.J.,Kim,D.Optimal and Heuristic Decision Strategies for Integrated Product and Marketing Planning[J].Decision Sciences,1993,24(6):1203～1213

Three-stage ITIO Decision-making Model Based on Marketing Cost

Li Fuchang

(Yunnan Normal University，Kunming 650500，China)

〔Abstract〕In general,the overall and individual optimization is inconsistent,there is a deviation between them,and this deviation lead to efficiency loss.Inventory-transportation integrated optimization(ITIO)integrating inventory and transportation costs into one problem,and finding the optimum solution of joint problem is rather than single problem,and can optimize the operating costs of the whole distribution system.Based on marketing cost,we establish three-stage ITIO decision-making model and analyze properties of the model.The study shows that:marketing cost elasticity of demand,order costs,start-up costs of production,production cost,variable costs and fixed costs of transportation have positive impact on retail price and marketing costs,while price elasticity of demand and the order quantity have negative impact.When order the same quantity,the marketing costs of ITIO is less than that of retailer-led separate optimization.

〔Key words〕marketing cost;ITIO;retailer;supplier

(责任编辑：王平)

作者简介：李富昌，云南师范大学经济与管理学院副教授，博士，硕士生导师。研究方向：物流管理。

基金项目：云南省中青年学术和技术带头人后备人才项目(项目编号：2014HB009)；国家自然科学基金资助项目(项目编号：71262031，71362029)；云南省级立项支持新增一级学科博士点学科建设规划(应用经济学)；云南师范大学“十二五”学科建设项目(一层次应用经济学)。

收稿日期：2015—10—23

中图分类号〔〕F830〔

文献标识码〕A

DOI：10．3969/j．issn．1004-910X．2016．02．006