孟群曜 芦俊杰 王佳辉 高宇辰 刘永露

摘 要:风流过一个通有电流的导体线圈,线圈的温度会降低。利用CFD计算技术,对由风速、线圈材料、线圈热功率等参数引起的温度变化进行了研究。在风速为1 m·s-1~50 m·s-1范围内,采用标准k-ε湍流模型,对通电线圈周围的热流场进行了数值模拟。结果表明:随着风速增大,线圈温度降低;随着线圈产热功率增加,线圈温度随之升高;线圈尺寸增大,温度升高;线圈材质对线圈温度没有影响。
关键词:风速;载流线圈;CFD
中图分类号:TJ206 文献标识码:A 文章编号:2096-4706(2021)02-0135-04
Abstract:When air flows through a conductor coil with current,the temperature of the coil will decrease. The temperature changes caused by the following parameters,such as wind speed,coil material,coil thermal power etc are studied by using CFD calculation technology. In the wind speed range of 1 m·s-1~50 m·s-1,the standard k-ε turbulence model is used to make numerical simulation on the heat flow field around the current coil. The results show that the coil temperature decreases with the increase of wind speed,the coil temperature increases with the increase of coil thermogenic power,the coil temperature increases with the increase of coil size,and the coil material does not affect the coil temperature.
Keywords:wind speed;current-carrying coil;CFD
0 引 言
热线风速仪由于检测元件小,热惯性小,灵敏度及空间分辨力高,对流态干扰小,能用于测量动态随机变量,是目前分析流体内部时空变化方面最为合适的量测仪器之一[1]。King提出了无限长线和流体之间的热对流理论[2]促使热线探头技术发展。这一理论是开发一些测控仪器,如热线风速仪等仪器的基本原理。探究并明确风速对线圈温度影响规律是开发这些测控仪器和设备的必要前提。在热线风速仪的设计与应用中,最为棘手的问题是流体的湍流对仪器测量精度的影响[3]。本文利用计算流体动力学(Computational Fluid Dynamics,CFD)技术,同时主要关注线圈的温度及周围传热情况,对湍流流体空气流经通电线圈这一过程进行模拟分析,为该过程提供了参考数据,有利于提高热线风速仪仪器的精度。CFD是近年来广泛应用的研究流体流动与传热的方法之一。国内外很多学者利用CFD相关理论知识[4,5],对传热线圈进行了深入的研究和分析。白云峰等[6]、张月红等[7]和吴坤等[8]采用数值模拟方法研究了线圈位置、感应加热系统精度等参数对温度场的影响;依据现有的研究结果,林志伟等[9]对恒功率式热膜风速计进行了设计。
CFD是通过计算机数值模拟求解流体力学控制方程,对流体流动等现象进行数值分析、研究和预测的学科[10]。
基于传热原理的理论分析可以得出风速与功率,温度差的关系满足:
式中:P为加热功率;I为加热电流;R为加热电阻;Tw为线圈表面温度;Tf是环境温度探头测得温度;A和B是与线圈材料和结构相关的常数;u为气体流速值。
由式(1)可以得出在导热功率恒定的情况下,线圈的温度差与气体的流速应该满足二次函数关系。本文利用计算流体动力学软件,研究了不同流速下,线圈加热功率、尺寸和材料对线圈温差的影响,探究二者在不同条件下的相关系数及估计标准误差。
1 模型及模拟方法
1.1 模型的建立
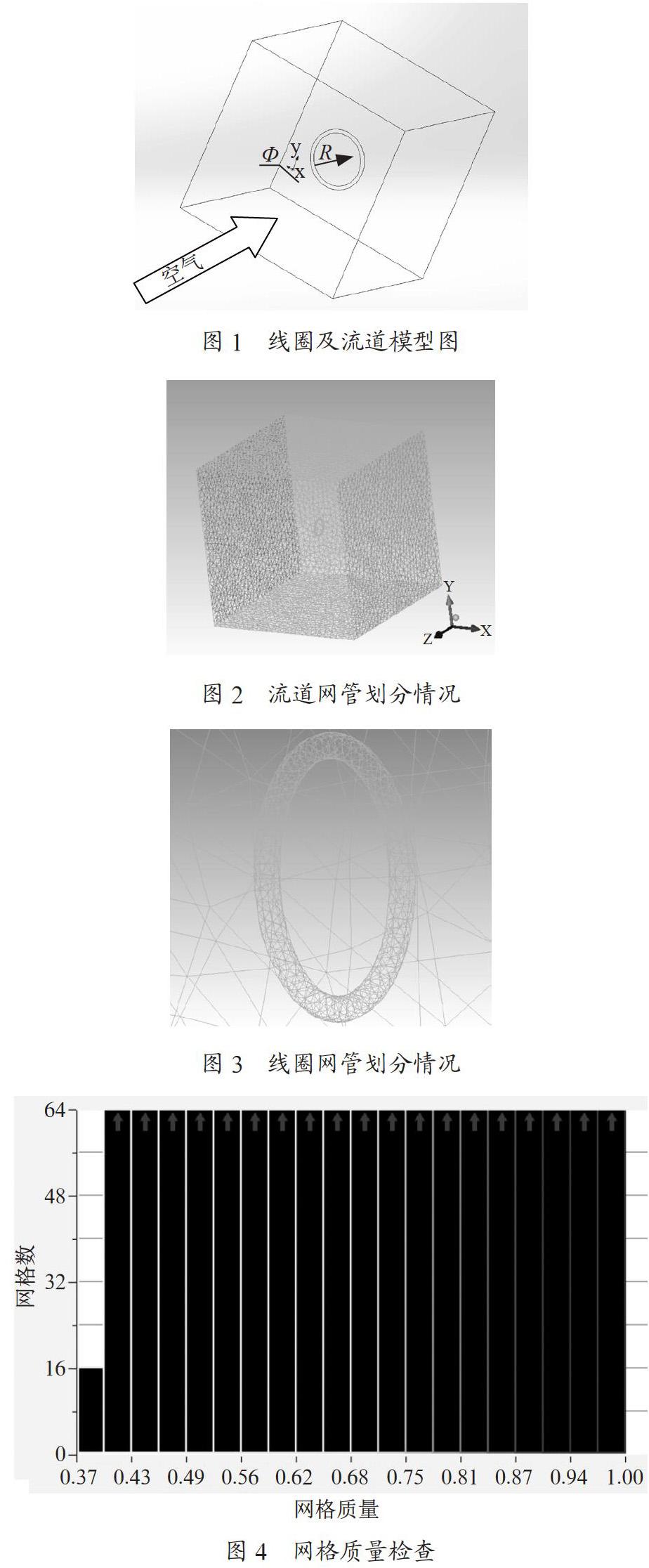
空气流通的通道为一正方体,圆环型线圈位于正方体中心。正方体流域的长宽高均为100 mm,线圈直径Ф=1 mm,1号圆环半径为R1=5 mm;2号圆环半径为R2=15 mm。通过改变进口风速、线圈尺寸及产热功率来计算不同参数下线圈的温度。计算模型如图1所示。
1.2 网格划分及网格独立性验证
采用正四面体非结构化网格对内置线圈的正方体流道进行了网格划分,为准确计算线圈附近的温度值,对线圈周围进行了网格加密处理。流道及线圈处网格如图2和图3所示。对通道网格整体的质量进行了检验,得到的网格质量值直方图如图4所示。由图4可见,网格质量大部分高于0.43,可认为网格质量良好。
为验证网格的独立性,排除网格的疏密程度对解的影响,对近线圈处进行了不同的加密处理,得到了5套节点数不同的网格。采用不同网格节点数目对线圈温度计算结果的影响如图5所示。由图5可见,当网格数量接近15万时,计算结果已与网格数量无关。综合考虑精度要求和计算资源,本文采用图中节点数为21万的网格进行计算。
1.3 控制方程及边界条件
本文采用标准k-ε湍流模型对内置产热线圈的正方体通道内的流体流动和传热进行了计算。稳态运行时的连续性方程、动量和能量守恒方程如式(2)~(8)所示。
式中:Gk为平均速度梯度引起的湍动能;Gb为浮力影响产生的湍动能;YM为可压缩湍流脉动膨胀对总耗散率影响的贡献;C1s、C2s、Cμ为常数。控制方程的边界条件及参数设定值如表1所示。采用速度和压力耦合求解方法,连续性方程、动量方程和能量方程的收敛条件为10-3、10-4和10-6,以空气为研究介质,改变入口速度计算不同条件下线圈的温度。
2 参数对线圈温度的影响
应用上述模型和计算方法,得到了如图6所示的流场温度等值线图,研究了风速、线圈尺寸及产热功率等多因素对线圈温度的影响。从图6可知,线圈温度远高于空气的温度,这是由于线圈内部有热量产生的缘故。线圈表面温度低于线圈内部温度,这是由于线圈表面有大量冷空气流动,线圈与冷空气之间进行的传导和对流传热降低了线圈的表面温度。
2.1 风速对线圈温度的影响
采用铝材质的线圈,在线圈直径为1 mm,圆环半径为5 mm,线圈产热功率P=1.0×107 W·m-3条件下,风速为1 m·s-1、5 m·s-1、10 m·s-1、20 m·s-1、30 m·s-1、40 m·s-1、50 m·s-1时,线圈的温度分别为376.0 K、347.6 K、338.8 K、332.9 K、329.0 K、325.5 K和322.7 K。以风速的平方根为横坐标,以线圈温度与空气温度差值的倒数为纵坐标,可得到如图7所示的线圈温度随风速的变化规律图。
从数据和图7可以看出,随着风速的提高,线圈温度降低,这是由于随着风速增大,线圈与空气之间的对流传热系数增大,单位之间传递的热量增多,因此在线圈加热功率恒定的条件下,风速越大,线圈表面温度就越低。从图7可以看出,风速的平方根与线圈温度和空气温度差值的倒数呈现一定的线性关系。利用线性回归可计算得到斜率b=0.004 8,截距a=0.009 4,相关系数η=0.991 5,说明二者线性相关。截距和斜率可用于计算式(1)中的常数。
2.2 线圈产热功率对线圈温度的影响
在线圈直径为1 mm,圆环半径为5 mm条件下,考察了线圈产热功率对线圈温度的影响。当线圈产热功率为P=1.5×107 W·m-3时,风速为1 m·s-1、5 m·s-1、10 m·s-1、20 m·s-1、30 m·s-1、40 m·s-1、50 m·s-1对应的线圈温度分别为420.1 K、367.0 K、356.7 K、349.3 K、343.6 K、338.3 K和334.1 K。产热功率对线圈温度的影响如图8所示。
参照2.1节中线圈产热功率P=1.0×107 W·m-3时线圈的温度,对比不同产热功率下线圈温度可知,相同气体流速时,线圈产热功率越大,其表面温度越高。这是由于当气体流速恒定时,线圈与空气之间的对流传热系数基本为一常数,由傅里叶传热公式Q=KAΔTm可知,当传热系数K和传热面积A一定时,增大传热量Q,传热温差会变大。因此当线圈产热功率变大时,线圈表面温度会升高。
利用线性回归计算出P=1.5×107 W·m-3时趋势线的斜率和截距,得斜率b=0.003 2,截距a=0.006 2,相关系数η=0.986 9。
由公式(1)可知,与线圈结构和材料相关的两个参数A和B分别正比于a×P,b×P,对不同产热功率下得到的数据进行整理,可得到如表2所示的对比结果。
由表2可见,本文所采用的两种功率下,b×P的值相同,a×P的值偏差为1%。说明本文模拟所取得的数据结果均符合理论公式,结果可靠。
2.3 线圈尺寸对线圈温度的影响
在线圈直径为1 mm,产热功率P=1.0×107 W·m-3时,考察了不同圆环半径对线圈温度的影响。当圆环半径R=15 mm时,风速为1 m·s-1、5 m·s-1、10 m·s-1、20 m·s-1、30 m·s-1、 40 m·s-1、50 m·s-1对应的线圈温度分别为661.1 K、453.9 K、413.1 K、373.4 K、356.5 K、346.6 K和340.2 K。结果如图9所示。
参照2.1节中R=5 mm时线圈的温度,对比不同产热功率下线圈温度可知,相同气体流速时,圆环半径越大,其表面温度越高。这是因为圆环半径增大,线圈产热功率增大,线圈产热功率与体积成正比,即Q与R成正比。虽然圆环半径增大,传热面积也增大,然而线圈与空气之间的传热面积A与R成正比。当风速一定时,线圈与空气之间的对流传热系数基本一定,因此由傅里叶传热公式可知,增大圆环半径,线圈温度增大。
利用线性回归计算出图9中趋势线的斜率和截距,得斜率b=0.003 6,a=-0.001 8,相关系数R=0.991 3。
2.4 线圈材质对线圈温度的影响
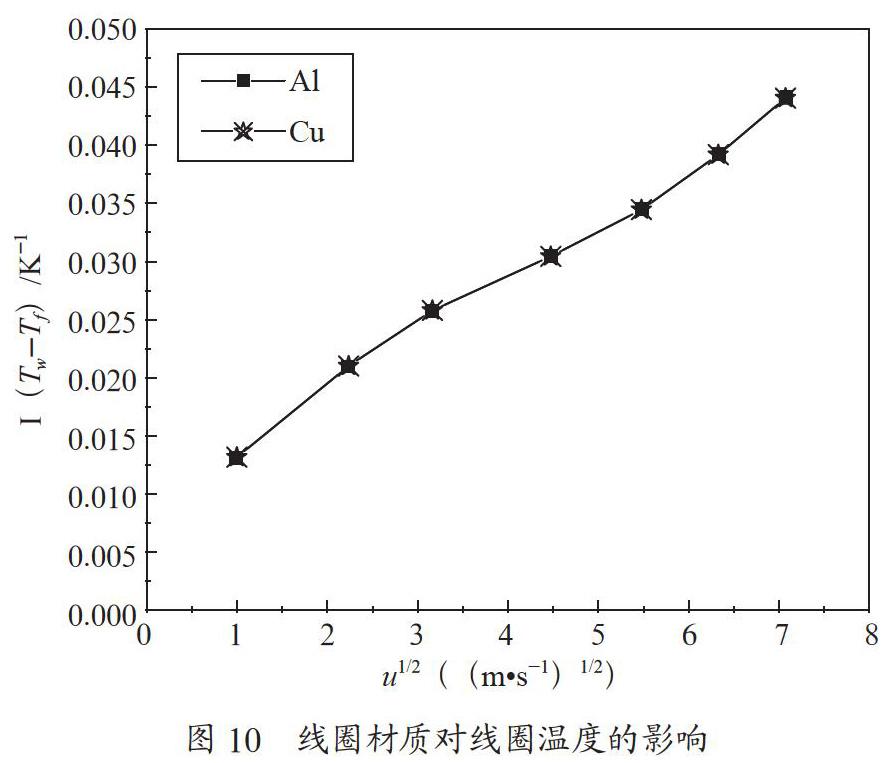
在线圈直径为1 mm,圆环半径R=5 mm,产热功率P= 1.0×107 W·m-3时,考察了不同材质对线圈温度的影响,结果如图10所示。
由图10可见,当产热功率和线圈尺寸相同时,线圈的材质对线圈温度几乎没有影响。这是因为尽管线圈材质不同,其导热系数差异较大,然而,在本文所研究的气速范围内,线圈与空气之间的传热主要由对流方式进行,而由传导方式传递的热量微乎其微。因此,尽管采用不同导热系数的材质进行模拟实验,在产热功率和线圈尺寸相同时,不同材质的线圈温度不会呈现出明显的差异。
3 结 论
本文采用CFD软件对正方形通道内风作用下的线圈温度进行了模拟计算,考察了风速、线圈产热功率、线圈尺寸和材质等多因素对线圈温度的影响。取得以下结论:
(1)利用数值模拟方法取得的线圈温度与空气温度差值的倒数与风速的平方根线性相关系数大于0.99;不同条件下得到的与线圈结构和材料相关的常数的偏差为1%;说明模拟结果可靠,所取得的数据可用于开发和设计与风作用下载流线圈温度变化相关的仪器设备。
(2)其他条件不变的情况下,增大风速,线圈温度降低;增大线圈产热速率,线圈温度升高;增大线圈尺寸,线圈温度升高;线圈材质对其温度几乎无影响。
参考文献:
[1] 刘祖唐,沈懋如.热线风速仪 [J].河海大学学报(自然科学版),1982(3):133-142.
[2] KING L V.On the Convection of Heat from Small Cylinders in a Stream of Fluid:Determination of the Convection Constants of Small Platinum Wires with Applications to Hot—Aire Anemometry [J].Philosophical Transactions of the Royal Society of London,1914,214(509-522):373-432.
[3] 韦青燕,张天宏.高超声速热线/热膜风速仪研究综述及分析 [J].测试技术学报,2012,26(2):142-149.
[4] 王福军.计算流体动力学分析:CFD软件原理与应用 [M].北京:清华大学出版社,2004.
[5] 韩占忠,王敬,兰小平.FLUENT:流体工程仿真计算实例与应用 [M].北京:北京理工大学出版社,2004.
[6] 白云峰.线圈接线位置对管坯感应加热温度场影响的数值模拟 [J].宝钢技术,2011(4):23-26.
[7] 张月红.感应加热温度场的实验与仿真研究 [J].企业科技与发展,2010(4):44-46.
[8] 吴坤.基于ANSYS的感应加热系统高精度仿真研究 [D].杭州:杭州电子科技大学,2014.
[9] 林志伟.恒功率式热膜风速计设计 [D].哈尔滨:哈尔滨理工大学,2014.
[10] 杨昂,张涛,卢学强,等.计算流体力学技术在膜分离过程中的应用与进展 [J].城市环境与城市生态,2013,26(6):20-23.
作者简介:孟群曜(2001—),男,满族,辽宁沈阳人,本科在读,研究方向:自动化;刘永露(1989—),男,汉族,重庆人,系副主任,副教授,博士,研究方向:电气控制。

