政府补贴、绩效激励与PPP模式的收益分配

肖 万 孔 潇

（华南理工大学工商管理学院，广州 510640）

PPP （Public－Private Partnership） 模式是政府和社会资本在公共服务领域建立的一种长期合作关系。这种合作关系，在降低政府财政负担和社会资本投资风险的同时［1，2］，也会在公私双方之间产生委托代理关系［3］。降低PPP模式的委托代理成本、设置有效的激励机制与收益分配机制，不仅关乎政府和社会资本方的利益，也是PPP项目持续健康运营的关键。

与一般合同相比，基础设施项目建设与运营的长期性、复杂性使得PPP合同更加不完备。因此，不断优化PPP合同条款的设计可以降低代理成本［4，5］。 但这些研究多是基于单一阶段， 缺乏对社会资本与政府长期合作关系不同阶段的研究，即这些研究的目标区间多为PPP项目整个特许期，没有考虑到特许期内的差异和风险变化。显然，不同的机制设计会对项目绩效、运营产生重要影响［6－9］。 而刘继才和刘珈琪 （2017）［10］、 范如国和杨洲 （2018）［11］将政府对社会资本的奖惩机制放大到政府与社会资本方的博弈，从一般原理或模型上分析了双方的博弈关系，但一定程度上脱离了PPP模式本身的差异与特点。

在PPP模式中，政府关注基础设施建设与社会福利，而私人部门关注自身的投资收益，两者的目标是不同的。如何保障社会资本方的利益，是确保PPP项目能否成功建设和持续运营的关键。 Ashuri等 （2002）［12］在二叉树定价模型的基础上通过计算公私双方的净现值，研究了政府的最低担保水平与私人部门的收益上限。吴孝灵等（2013）［13］以PPP项目实际收益与特许收益的差异为基准，研究了政府给予私人部门建设期和运营期的补偿值，并分析了政府的最优补偿机制。朱建波等 （2016）［14］研究发现，私人部门超额收益增加与政府监管成本上升都能推进合作，并研究了超额收益的最优分配系数。这些研究，在PPP模式治理机制以及收益分配量化研究中取得了重大进步，但依然有很多问题需要深入研究。本文在前人研究的基础上，深入分析了PPP模式激励机制设计对社会资本的作用，这种作用反过来会对政府补贴、社会资本收益以及政府补贴与超额收益分配的关系产生影响。为此，考虑到PPP模式生命周期长、经营风险大的特点，本文尝试将项目经营期分为补贴期、超额收益期，并构建两阶段委托代理模型与绩效激励模型，将社会资本努力水平纳入绩效考核体系，分析其对项目需求量、补贴时间的影响。在此基础上，本文研究了政府对社会资本补贴与分成比例之间的关系。

在PPP项目中，政府部门与社会资本的目标是不同的。社会资本的目标是在保证自身参与约束最低的情况下追求其收益目标函数的最大化。PPP项目风险高、生命周期长、投资额大，政府一般要向社会资本提供一定形式的担保、便利、补贴才能吸引到社会资本参与PPP项目，以使其达到参与约束的最低收益标准。同时，政府也可能限制社会资本的超额收益，以维护PPP项目的社会公益性质。如政府会对社会资本所获得超额收益进行分成，以此来平衡政府财政收支并在一定范围内将社会资本产生的外部性内部化。

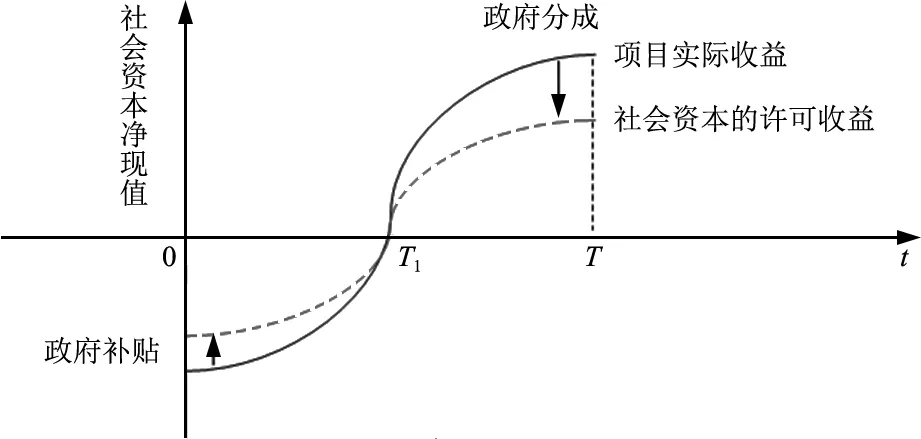
图1 社会资本净现值

对于政府而言，其与社会资本合作并主要为社会提供公共产品和服务，并不以自身的收益最大化为目标。因此，只要政府在PPP项目中为社会资本提供的补贴与从社会资本处获得的分成相等时，此PPP项目就是有价值且值得投资的。

构建该模型时以资产评估的收益法为基本原则，以社会资本为基础分析对象，采用现值的概念，以一定的折现率将社会资本的未来预期收支折算为评估基准日的现值，并将未来各期收支现值的算数和作为社会资本的净现值。通过上述方法综合分析PPP项目中社会资本的成本收益，并对不同阶段的情况进行具体研究。

假设1：PPP项目的运营分为政府补贴期和超额收益期两个阶段。假设收费价格是在运营期开始时 （t＝0）确定的，而此时，建设期的全部支出为已知，令其为C0。

假设2：社会资本以追求自身收益最大化为目标；政府部门主要为社会提供公共产品，只要为社会资本提供的补贴与从社会资本获得的分成相等，该项目就是物有所值（Value For Money，VFM）的。

假设3：社会资本确定收费价格时，政府部门与社会资本能够获得关于需求量与成本收益的相同信息，即双方的信息是对称的，但不一定是充分的。

假设4：收费价格p在整个特许期内保持不变，且第t年的需求量qt可表示为初始需求量q0与期望增长率∂的非线性函数。同时为了简化模型，假设PPP项目中不存在税收。

忽略PPP项目建设期的时间，PPP项目第t年的需求量可表示为关于q0与∂的非线性函数，将其定义为：

其中，初始需求量q0可通过历年需求量的数据分析确定；假设项目第t年需求量的近似值为Qt（t＝1，2，…，T）， 则需求量期望增长率∂的估计值为：

王卓甫等 （2017）［15］认为，随着运营过程的推进，项目运营成本下降，项目质量以及普及度、认可度进一步提升，因此每年的需求量将会持续增长。

第一阶段为政府补贴期。社会资本开始PPP项目的运营，此时消费者的支付意愿不高，市场的需求量相对较低。为防止社会资本现金流断裂乃至项目中止，同时也为社会资本收回投资提供保障，使社会资本能持续运营并改善项目质量，政府根据社会资本每年的净现金流量以α（0＜α≤1）的比例提供补贴。

假设政府补贴持续至第T1年，PPP项目的总特许经营期为T年。社会资本每年的成本、收益可表示为需求量qt的函数C（qt）、π（qt）， 即：

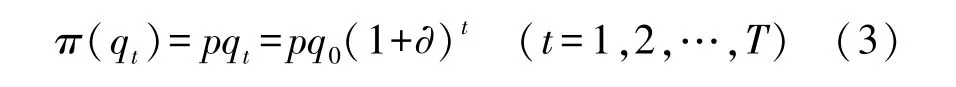
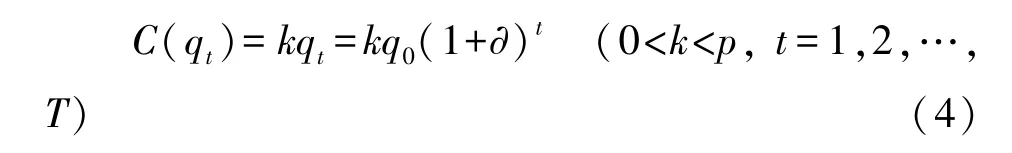
其中，k为社会资本的边际运营成本，k越大则每单位需求量增加所引起的运营成本的增加额越大。因为整个特许期内PPP项目的收费价格始终为p，因此，边际运营成本k低于收费价格p。

因此，政府补贴期内社会资本获得的补贴总额为：

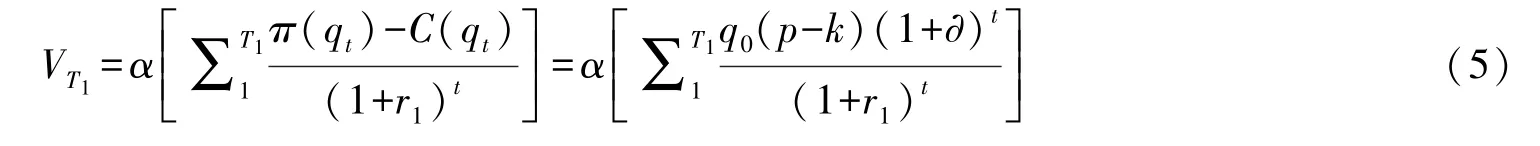
政府部门根据社会资本每年的净现金流量以α的比例进行补贴，但不对社会资本的初始建设成本C0提供补贴。

根据以净现值为基础的成本－收益分析法，第一阶段社会资本的利润函数ST1（若为负值则为亏损）可表示为：

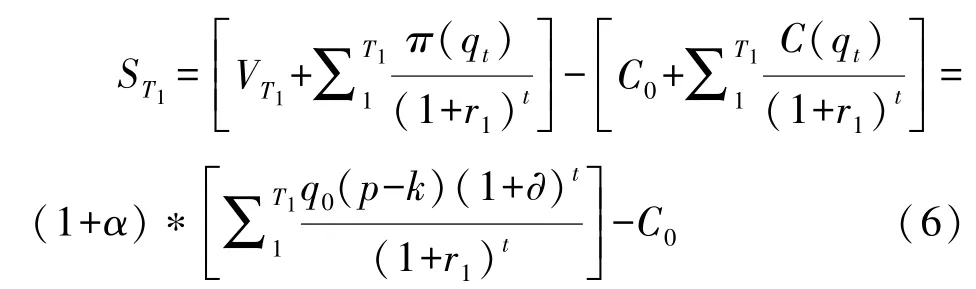
其中，r1为社会资本在补贴期内确定的折现率。

第二阶段为PPP项目的超额收益期。时间自第T1年至第T年。设第T1年时社会资本的净现值首次大于等于0，所获利润达到社会资本参与约束的标准。为了防止损害社会整体福利水平，也为了平衡政府整体的财政收支，政府对社会资本的超额收益部分以比例β（0＜β＜1）进行分成，那么，第二阶段超额收益的总分成额W可表示为：

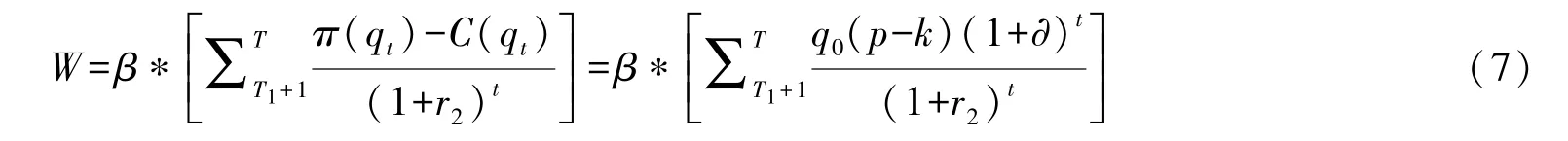
其中，r2为政府部门与社会资本经谈判所确定的超额收益期折现率。

第二阶段超额收益期中，社会资本所获得的实际利润因政府部门的分成而有所下降，因此，可将社会资本第二阶段的利润函数ST－T1表示为：

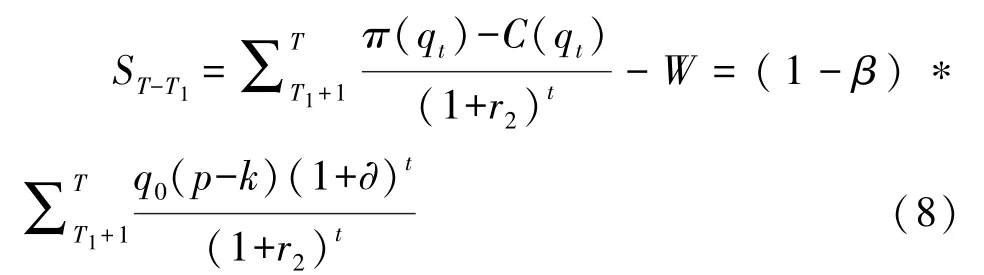
综上，社会资本在第一阶段政府补贴期的利润函数为ST1，第二阶段超额收益期的利润函数为ST－T1，故社会资本的总利润函数S可表示为：

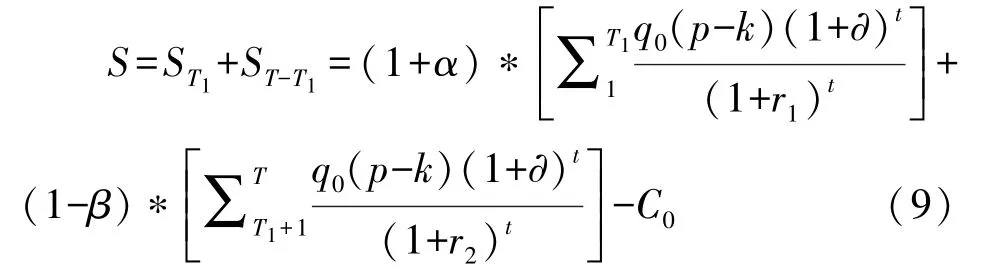
根据前述假设，政府只要在收付实现制的会计意义上实现了收支相等，即认为项目实现了物有所值。因此，对于政府部门，有下式成立：

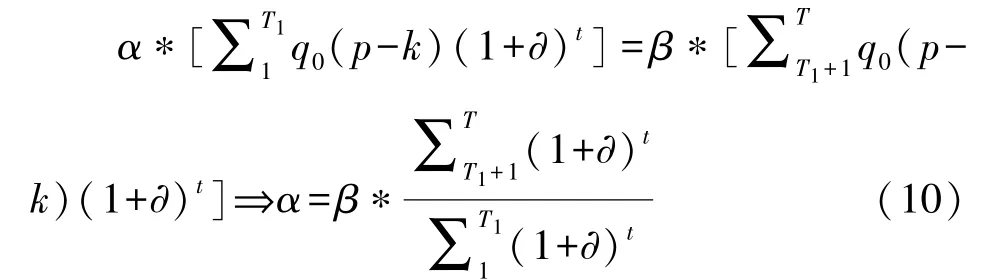
在不考虑政府部门与社会资本之间因委托代理产生代理成本的情况下，社会资本的总利润函数S可表示为：

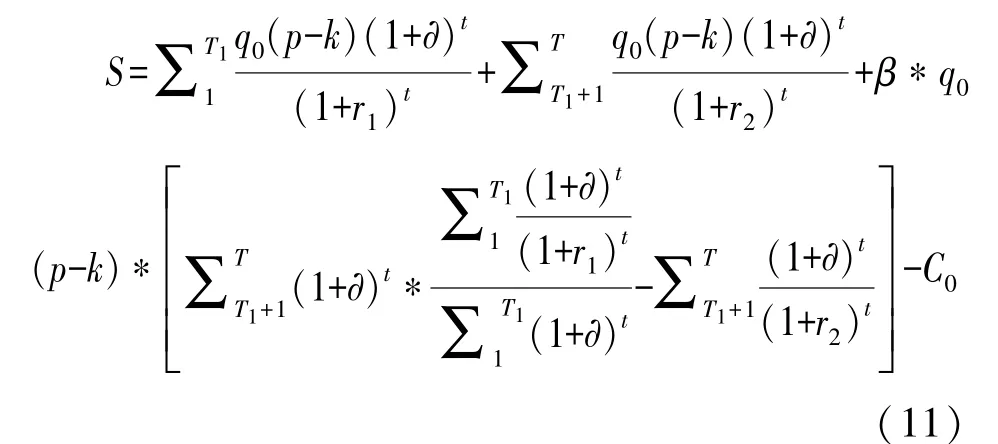
为了激励社会资本实现利润最大化，同时项目物有所值，可将其归纳为两个约束条件，即参与约束 （Individual Rationality Constraint，IR，也译为个人理性约束）和激励相容约束 （Incentive Compatibility Constraint， IC）［16］。

（1）参与约束 （IR），即社会资本参与PPP项目所获得的期望效用不小于未参与的效用时，社会资本才会选择参与PPP项目的建设与运营。社会资本不参与PPP项目时的最大效用一般是社会资本的最低保留效用，或可将其视为社会资本的机会成本，设为θ。当PPP项目的期望效用小于θ时，社会资本不会参与此PPP项目。因此，社会资本的参与约束 （IR）可以表示为：

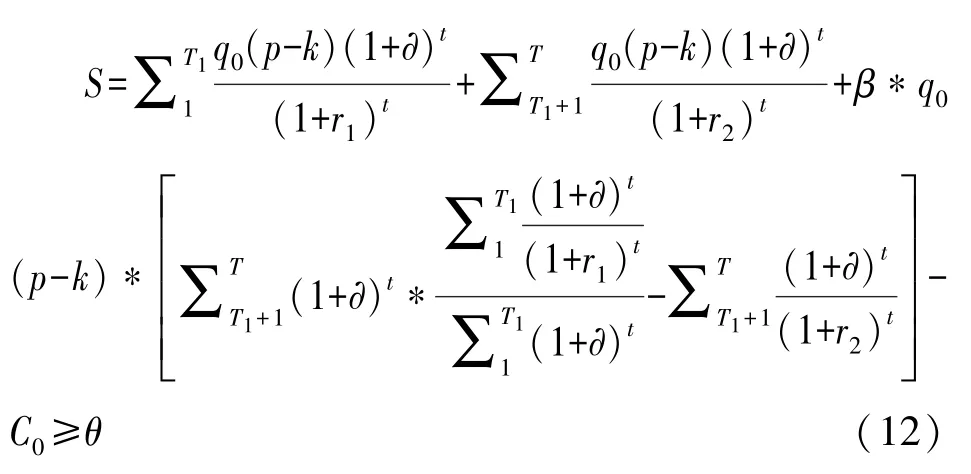
（2）激励相容约束 （IC），在信息不对称的情况下，政府部门会通过设计激励机制使社会资本实现利润最大化的同时实现物有所值的期望，此时社会资本的边际收益与边际成本相等。故激励相容约束 （IC）可表示为：

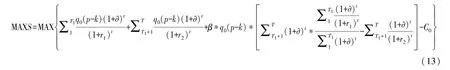
在两阶段委托代理模型中，当政府部门不追求自身的收益最大化，而仅追求物有所值时，社会资本的总利润函数S与分成比例β成线性关系，即当模型满足参与约束与激励相容约束的条件下，β（0＜β＜1）取其可行域内的最小值时，社会资本能够实现利润最大化。

（1）假设政府补贴期的折现率r1与超额收益期的折现率r2相等，令r1＝r2＝r，则社会资本的总利润函数S可以简化为：

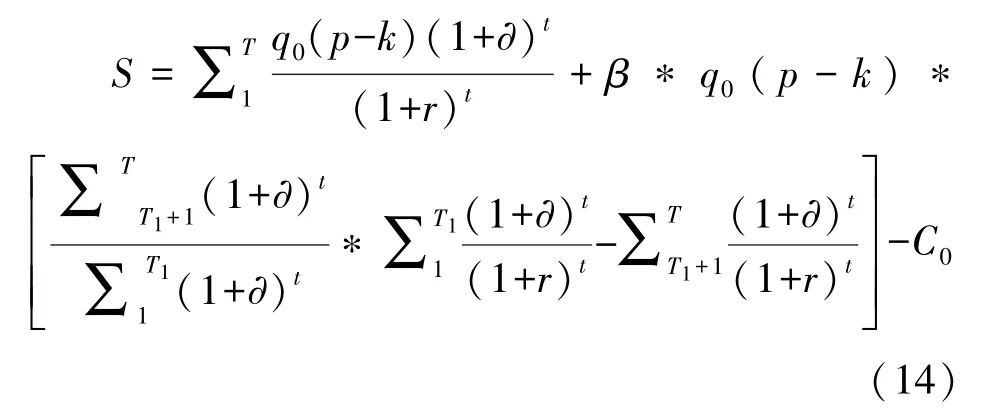
（2）考虑补贴比例α与分成比例β。当社会资本第一阶段所得利润与参与约束标准θ一致时，可通过表达式 （6）将补贴比例α表示为：

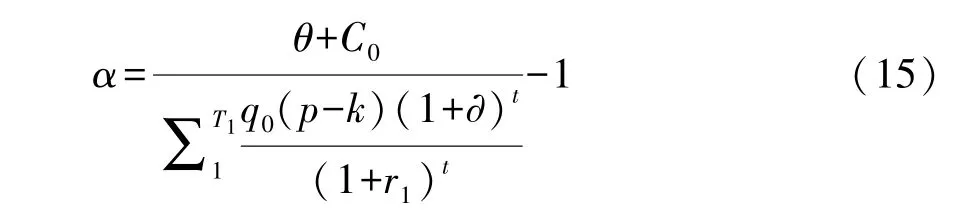
可见，补贴比例α由模型中多个变量共同决定。α与初始建设成本C0、折现率r1呈正相关关系，而与初始需求量q0、单位经营利润p－k、需求量增长率∂呈负相关关系。

当社会资本第二阶段的利润函数ST－T1＝φ时，根据表达式 （8）政府部门的分成比例β为：

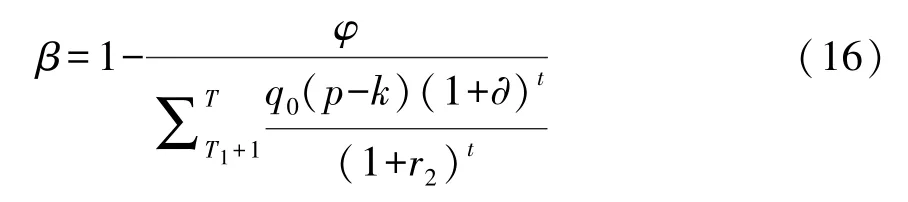
可见，类似补贴比例α，分成比例β由模型中同类变量决定，但与其正负相关关系不同。β与初始需求量q0、单位经营利润p－k、需求量增长率∂正向相关，而与折现率r2负向相关。

（3）考虑时间点T1的适用范围。当社会资本净现值首次不小于0的年份T1＞T时，即社会资本为收回投资且使净现值不小于0的时间超过了其特许经营期时，对社会资本而言，PPP项目的净现值为负，这显然不满足参与约束；当0＜T1≤T且社会资本总利润函数S≥θ时，社会资本的参与约束才能被满足，PPP项目才能够进行建设与运营。

在两阶段委托代理模型中，社会资本为了获取更多的利润可能会出现投机行为，如社会资本可能故意消极怠工、恶意增加成本或延长政府补贴期的时间。因此，在两阶段委托代理模型中不一定能够实现社会总体福利的最大化。政府部门为防止社会资本出现上述投机行为，考虑引入社会资本的努力水平，以原两阶段委托代理模型为基础，视原模型努力水平为0，并构建存在努力水平情况下的绩效激励模型。

社会资本的努力水平会影响PPP项目的效率，一定的努力水平能够提高项目经营质量并增加项目的额外收益，使公私双方均能从中受益。努力水平主要表现为社会资本在创新创造、技术研究、流程优化、服务提升等方面的努力程度。

具体而言，一定的努力水平会影响政府部门对社会资本的补贴比例和分成比例，影响政府补贴期的持续时间并增加PPP项目的需求量，从而提高社会资本的利润水平和整个社会的福利水平。

假设5：设h为社会资本的努力水平系数。h＞0时，表明社会资本付出正向努力以提升PPP项目的整体效率。

假设6：社会资本的努力水平会影响PPP项目的需求量， 参考 Taylor （2002）［17］的研究， 将PPP项目的需求量表示为关于努力水平h与需求量期望增长率∂的函数，则绩效激励模型中第t年的需求量可表示为t＝q0∗（1＋ah）（1＋∂）t。 其中，a为社会资本努力水平对需求量的影响系数，且a∈［0，1］， 同时满足（1＋ah）≥0。 因此， 在前述两阶段委托代理模型需求量q0（1＋∂）t的基础上，社会资本每单位努力水平的提升将带来q0∗（1＋a）（1＋∂）t单位需求量的增加。

假设7：社会资本付出努力以提高效率时会产生相应的努力成本。努力成本C（h）可表示为努力水平的函数， 令C（h）＝μh2／2 （μ＞0）， 满足C′（h）＞0，C″（h）＞0， 且μ为社会资本的努力成本系数，一般取大于0的常数。

假设8： 根据函数C（h）＝μh2／2的导函数可知，努力成本为边际递增的，一定存在最优的努力水平h∗（h∗＞0），使得社会资本达到利润最大化。因此，社会资本将选择h∗作为自身的最优努力水平。

假设9：假设政府部门为激励社会资本达到最优努力水平，会调整补贴比例α与分成比例β。设补贴比例和分成比例分别为、，且满足∈（0，1］、∈（0，1）。

社会资本的努力会提升项目效率，在同等条件下能够缩短政府补贴期的时间。在项目特许期T不变的情况下，第二阶段超额收益期将增长，从而增加PPP项目的总体利润，增强了对社会资本的激励程度。在社会资本以一定努力水平运营项目的情况下，第一阶段政府补贴期将缩短为Th：

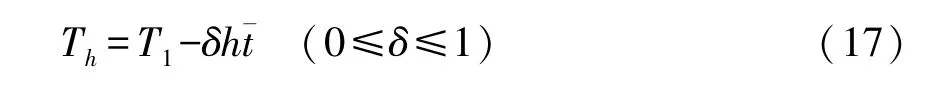
其中，T1为原两阶段委托代理模型中的政府补贴期，δ（0≤δ≤1）表示社会资本努力水平对PPP项目补贴期的影响系数，为绩效激励模型中可视为常数的单位时间。可见，社会资本所付出的努力能够使政府补贴期的时间缩短δh年。则PPP项目总特许期T不变，第一阶段政府补贴期缩短且至第Th年结束。

引入社会资本努力水平后，PPP项目两个期间的时间发生变化，根据假设6，绩效激励模型中PPP项目第t年的需求量t为：

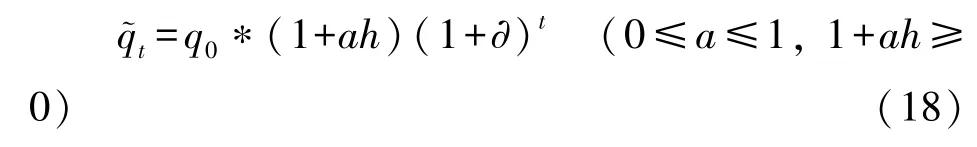
在收费价格p保持不变的情况下，社会资本第t年的收益为：

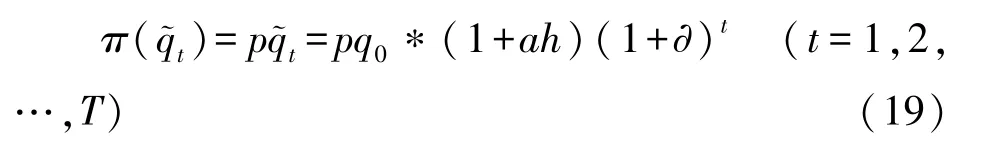
设社会资本第t年的运营成本与需求量t正相关，则社会资本第t年的运营成本C（）为：

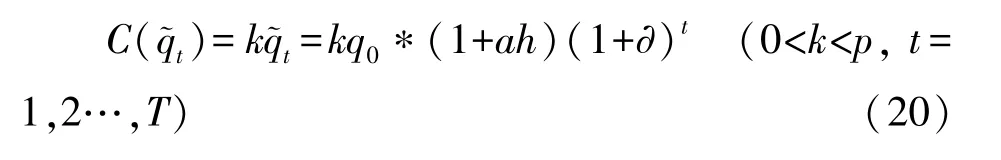
第一阶段政府补贴期中，根据假设9，政府将根据社会资本净现金流以（0＜≤1）的比例提供补贴。同时根据假设7，社会资本在PPP项目中付出的总努力成本为C（h）＝μh2／2 （μ＞0），每年的努力成本为C（h）的平均值，则社会资本在PPP项目特许期内每年的努力成本可表示为μh2／2T（μ＞0）。因此，社会资本在政府补贴期所获得的总补贴为：

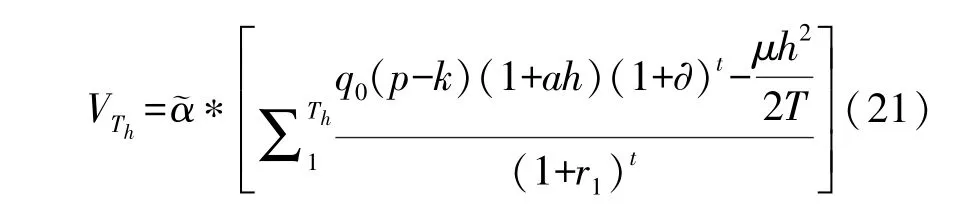
其中，社会资本因自身努力水平提升，所获得的利润增加，各年利润大于其努力成本。另外，在两阶段委托代理模型与绩效激励模型中，虽然二者补贴期的持续时间不同，但在补贴期末都实现了社会资本的净现值为0，即达到了社会资本参与约束的总利润标准θ，因此绩效激励模型中政府补贴期的折现率仍为r1。

在此情况下，第一阶段政府补贴期社会资本利润函数STh（若为负值则表示亏损）为：

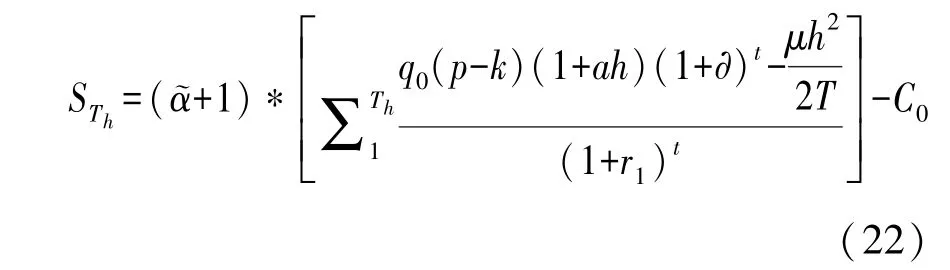
当社会资本的总利润达到参与约束标准θ，即自第Th＋1 年开始， 政府部门将以比例（0＜＜1）对社会资本的超额收益进行分成。因此，政府部门在超额收益期获得的总分成额可表示为：

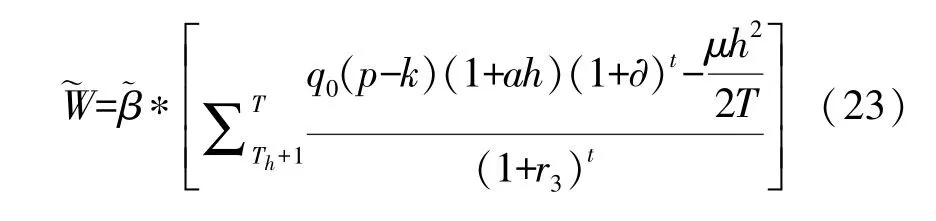
其中，r3为绩效激励条件下超额收益期内的折现率。

因此，社会资本在超额收益期内的利润函数ST－Th为：

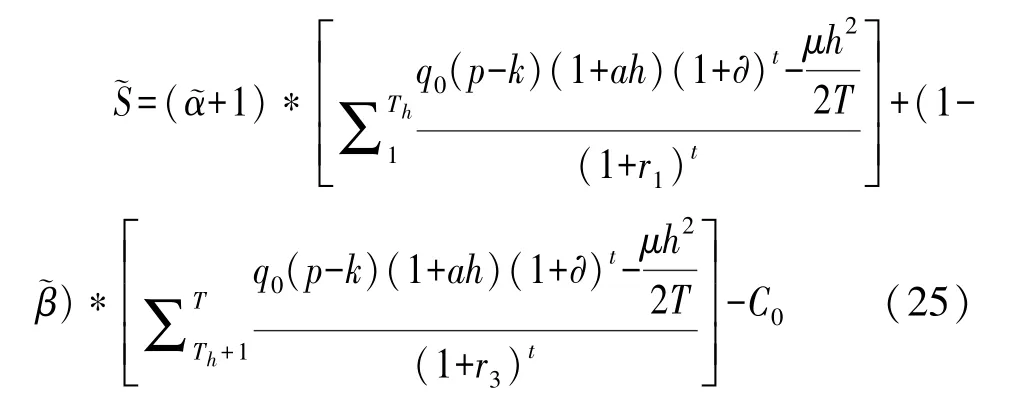
另外，PPP项目物有所值，则政府部门在整个项目中给予社会资本的补贴与从社会资本处获得的分成应相等，可将其表示为：

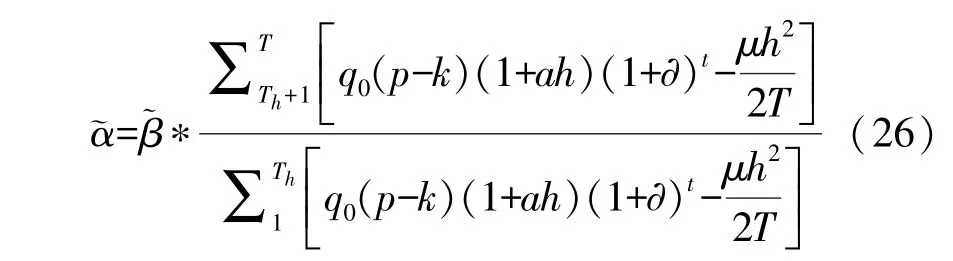
忽略政府部门与社会资本间因委托代理关系而产生的代理成本，则社会资本的总利润函数可表示为：

则上式可以简化表示为：

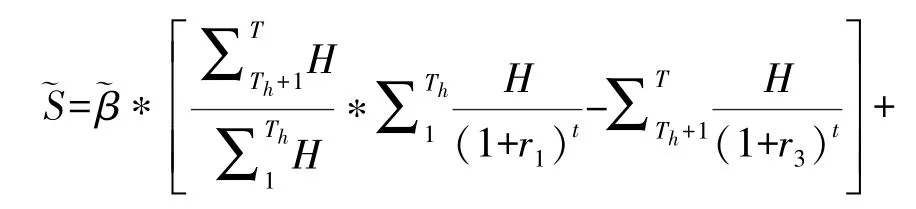
参考上述两阶段委托代理模型，得到绩效激励模型中的参与约束 （IR）与激励相容约束 （IC），可将其表示为：

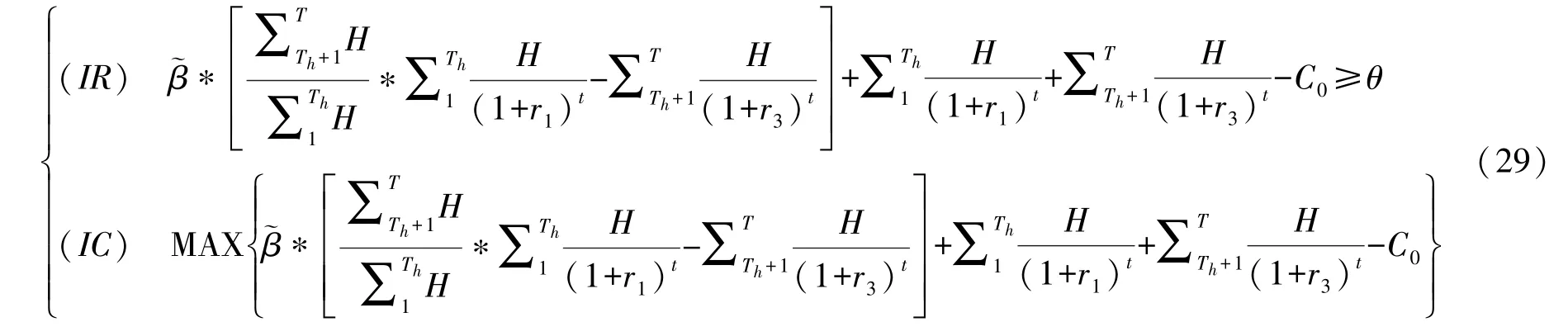
（1）假设在绩效激励模型中，社会资本在两个阶段的折现率r1与r3相等，取r1＝r3＝r，则社会资本的总利润函数可以简化表示为：

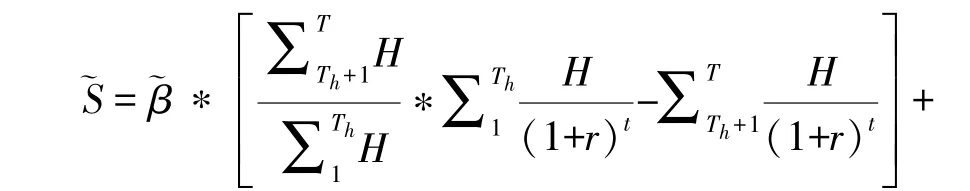
根据上述假设8，存在最优的努力水平h∗使社会资本实现利润最大化。因此，对社会资本总利润函数求努力水平h的偏导数，即令，可得最优的努力水平为：

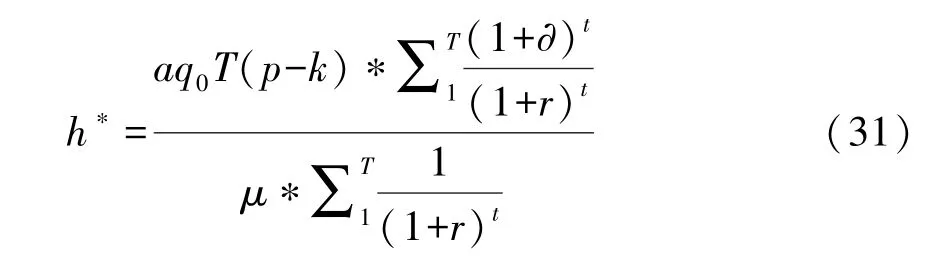
可见，社会资本的最优努力水平h∗由收费价格p、PPP项目特许期T、初始需求量q0、社会资本的努力成本系数μ、社会资本努力水平对需求量的影响系数a共同决定，且随需求量增长率∂与折现率r而变化。在未达到最优值的情况下，h与T、a成正比；h与μ成反比。

在社会资本选择最优努力水平h∗的情况下，绩效激励模型中参与约束 （IR）与激励相容约束（IC）可用下式表示：

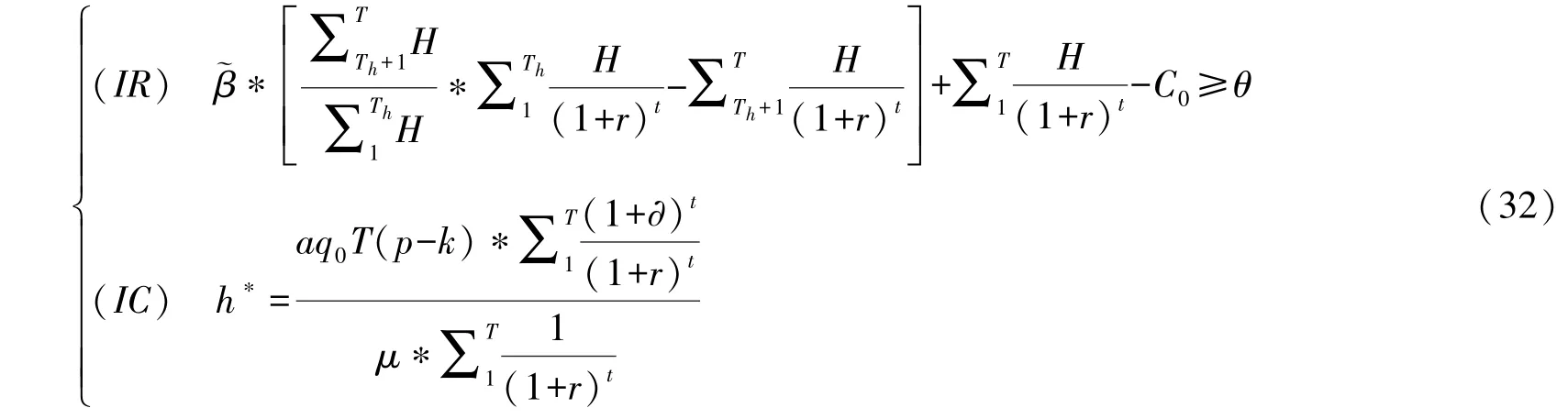
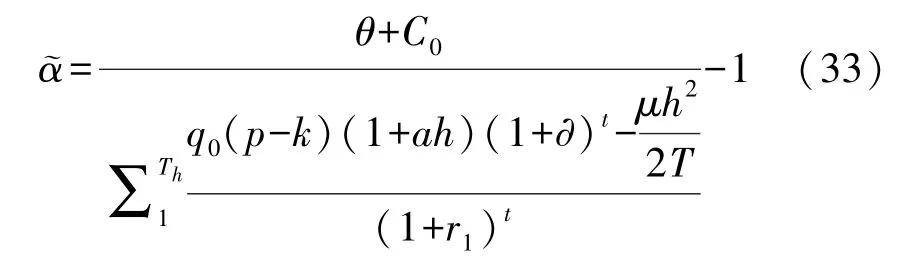
当社会资本超额收益期的利润函数ST－Th＝η时，根据式（24）可将分成比例表示为：

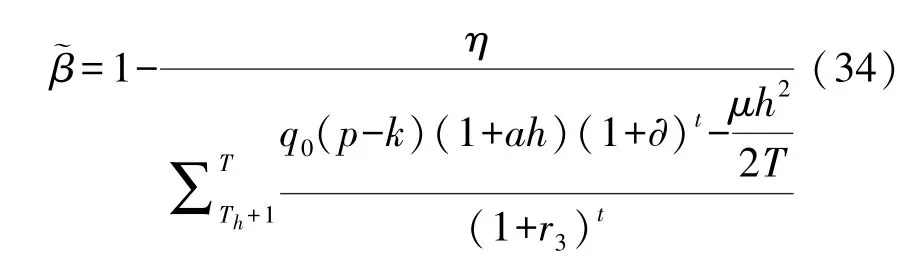
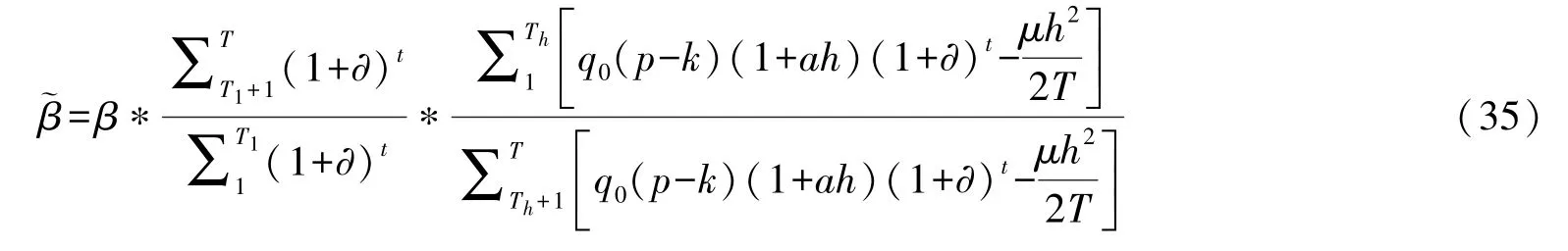
当绩效激励模型满足激励相容约束取最优努力水平h∗时，与β的关系式可转换为：

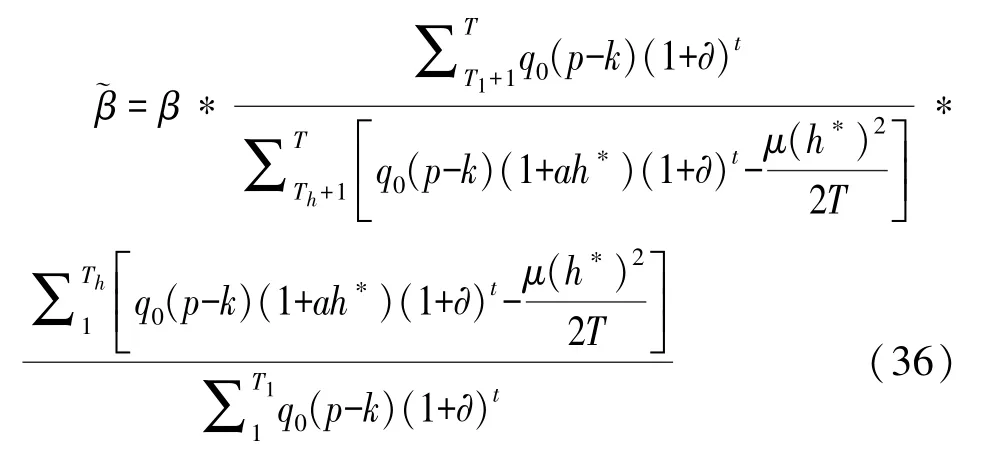
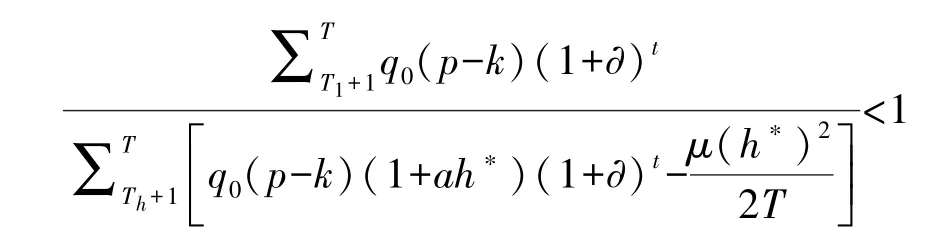
因Th＜T1，且在项目初期需求量指数型增长特征并不明显，在扣除努力成本后仅能保证每期运营利润为正，因此绩效激励模型小于两阶段委托代理模型在政府补贴期的运营利润，即：

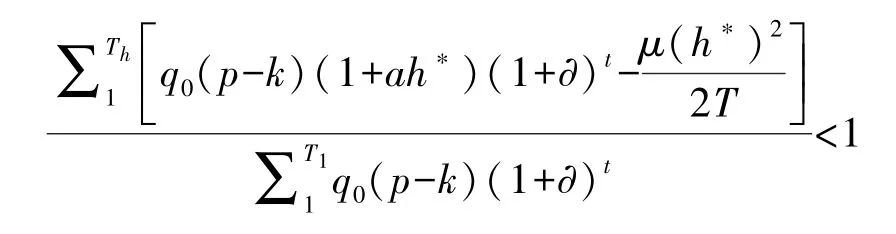
（4）考虑绩效激励模型中第t年的需求量。与无激励相比，绩效激励情况下PPP项目的需求量为前者的（1＋ah∗）倍。显然，社会资本的运营成本、收益也为原来的（1＋ah∗）倍。

（5）考虑社会资本的总利润。因为存在绩效激励，根据式 （14）与式 （30），社会资本总利润的差值为：

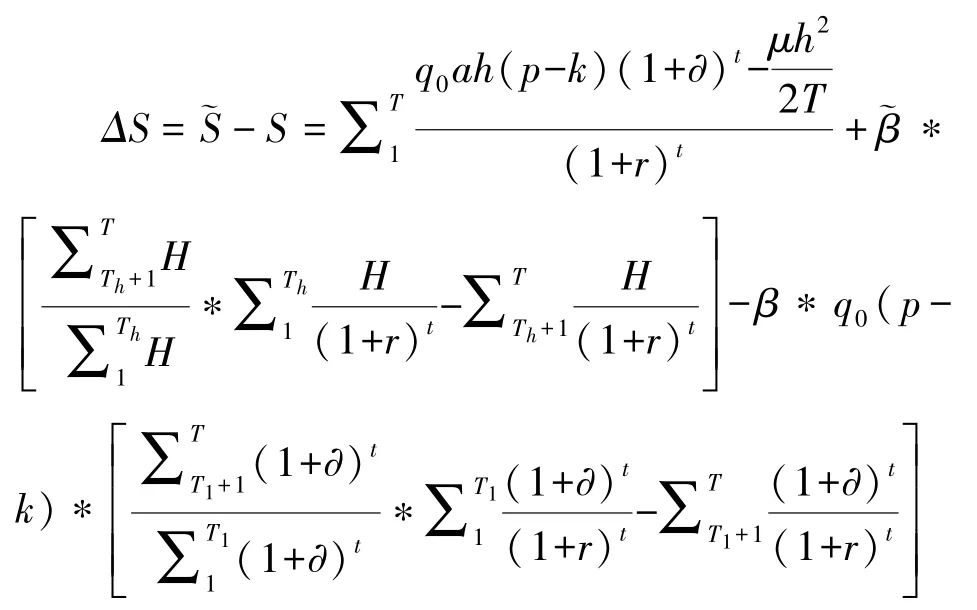
可见，在上述激励机制下，社会资本的总利润不低于两阶段委托代理模型中的总利润，即存在ΔS≥0，即社会资本能够实现项目运营的帕累托改进。

综合来看，当存在绩效激励且社会资本的努力水平达到h∗时，总利润达到极大值。所以，政府部门应通过激励机制的设计使社会资本的努力水平在项目特许期内达到h∗。但社会资本努力水平不易观测，因此，可通过PPP项目的需求量间接衡量社会资本努力水平。若第t年的项目需求量， 则说明社会资本付出的努力水平不小于最优努力水平h∗。但社会资本总是理性的，在其追求利润最大化的过程中，付出超过h∗的努力水平将使自身的总利润降低，因此，当社会资本的努力水平达到h∗时，其并不会继续提升努力水平。若第t年的项目需求量， 则说明社会资本实际付出的努力水平小于最优标准h∗，即当社会资本的努力水平h∈［0，h∗）时，由于努力成本函数C（h）的存在，社会资本的总利润函数将随努力水平的增加而呈曲线变化，总利润函数为二次函数。即在h∗之前，社会资本努力水平的提升使其获得利润的增加高于付出的成本。

另外，当社会资本的努力水平h＜0时，社会资本付出负的努力水平，即社会资本处于 “消极怠工”的状态，此时项目需求量将小于基础需求量q0∗（1＋∂）t，政府将对社会资本进行惩罚，取消对社会资本的所有补贴。而且，此时社会资本依靠项目运营收益将无法满足参与约束的最低保留效用θ，从而促使社会资本竭力提高自身的努力水平。

（6）考虑政府部门补贴比例与分成比例在模型中非固定的情况。存在绩效激励的情况下，假设与并非始终保持不变，而是根据社会资本每年的盈亏与程度大小进行阶段性设置。如将补贴比例设为3个值，将政府补贴期内社会资本的净现金流量对应分为3个阶段，净现金流量越大则获得的补贴比例也越大，从而提高了对社会资本的激励强度。

广东省中山市拟修建一条高速公路并采用PPP模式建设与运营。该高速公路全长40.7km，项目特许期为20年，社会资本初始建设成本为22.19亿元，初始交通通行量预计为4万辆／天，通行费用平均为10元／辆，通行量的年期望增长率为5%，项目边际运营成本为3元／辆。

（1）两阶段委托代理模型中政府补贴期为13年，折现率r1为5%；超额收益期为7年，折现率r2为10%。将上述指标代入式 （6），当社会资本净现值为0时，可得：

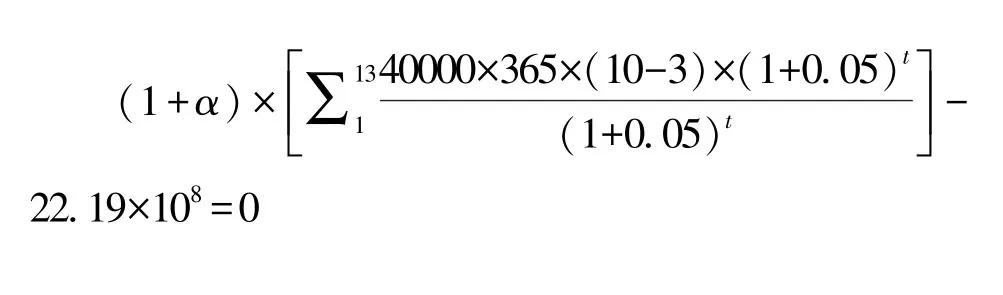
求解得：

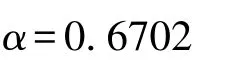
当补贴比例α为67.02％时， 根据补贴比例与分成比例的关系式（10），可得：

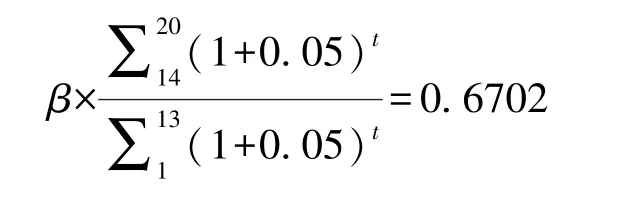
求解得：

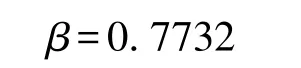
当不考虑政府与社会资本之间的代理成本时，根据式 （11），两阶段委托代理模型中社会资本总利润S为7394.92万元，则在满足上述约束条件下使得社会资本利润最大化的分成比例β为77.32%。

（2）在绩效激励模型中，努力水平对需求量的影响系数a为0.15，社会资本努力成本系数μ为0.5，努力水平对项目补贴期的影响系数δ为0.7，超额收益期折现率r3为12%，项目特许期仍为20年。由式 （31）可知社会资本的最优努力水平h∗为2.59， 则根据式 （18） 第t年的需求量可表示为：

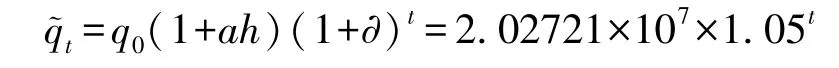
根据式 （17），政府补贴期Th变化为：

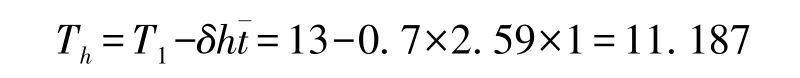
近似取Th为11年，则绩效激励模型中超额收益期为9年。

同理，在政府补贴期内，当社会资本净现值为0时，由式 （22） 可得：

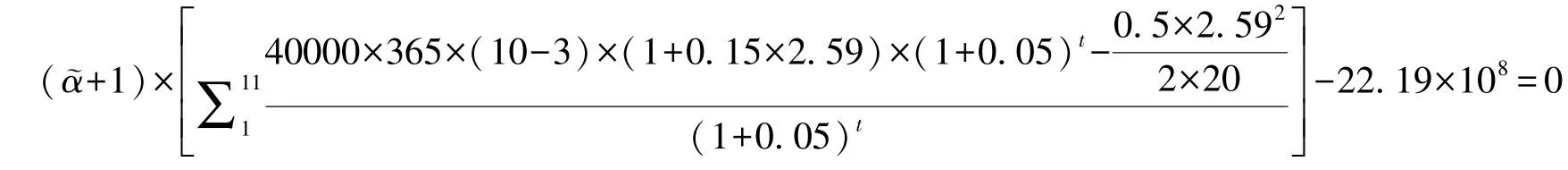
求解得：

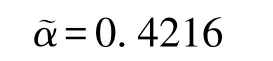
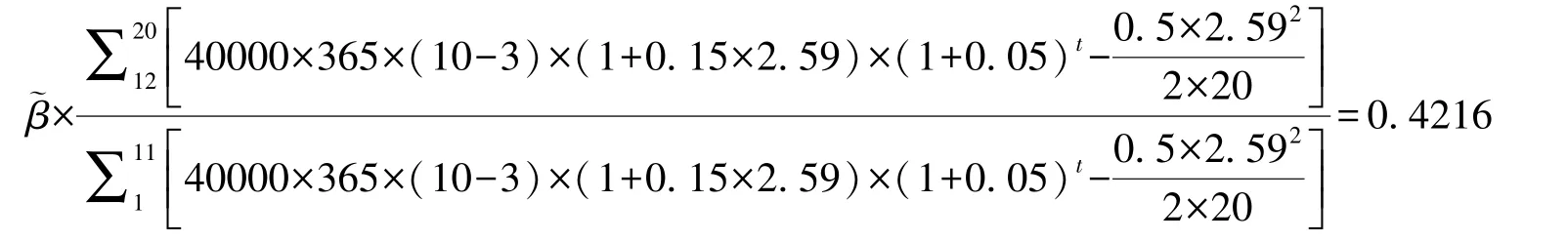
求解得：

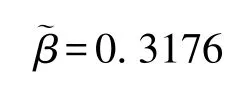
综上，由式 （27）可知，社会资本最优努力水平为h∗且分成比例为31.76%时，其总利润为3.147亿元。

（3）综合分析发现，绩效激励模型中社会资本的最优努力水平使政府、社会资本、项目本身和公众都获得了好处。这种对社会资本的激励，在缩短政府补贴时间的同时也使补贴比例下降，即＜α。而且，激励使项目的需求量增加且社会资本的超额收益期得到了延长，社会资本的总利润大幅上升，即＞S。另外，政府对社会资本的分成比例下降，即＜β，从而在两阶段委托代理模型的基础上进一步增大了激励强度，改善了PPP项目的效率，提升了社会资本的收益，这为PPP模式在全社会的持续运用创造了条件。

本文考虑了PPP模式中社会资本努力水平、努力成本、需求量期望增长率等因素，构建并对比了两阶段委托代理模型与绩效激励模型，量化分析了社会资本的最优努力水平与最大期望效用，并进一步讨论了政府对社会资本补贴比例、分成比例的确定方法、影响因素及其相互关系。研究发现，PPP模式中对社会资本进行的绩效激励，能使社会资本提高努力水平，延长超额收益期，还可以降低政府分成比例。对政府而言，虽然其分成比例降低了，但相应的其对社会资本的补贴期缩短且补贴比例降低。即因合同所确立的绩效激励制度，使社会资本、政府、社会公众均获得了效用的提升。

因此，为缓解PPP项目中社会资本参与度较低的问题，并优化公私双方的收益分配，本文提出下述建议：（1）完善激励机制与绩效考评机制的设计和实施。政府应避免频繁利用自身权力优势对社会资本进行过度约束，而应通过合理的机制设置激励社会资本提升努力水平、降低运营成本； （2）政府对社会资本的补贴要与从社会资本处获得的收益分成密切联系，从而降低政府的财政负担，使项目能通过 “物有所值（Value for Money，VFM）”评估。过高的补贴比例不仅会诱使社会资本为获取更高的补贴而不愿意付出努力，而且增加了政府的财政负担，降低了项目的价值，社会公众的福利与需求将不能得到满足。