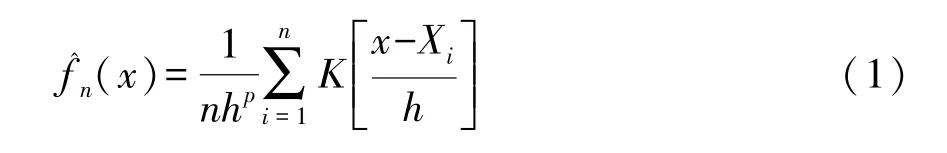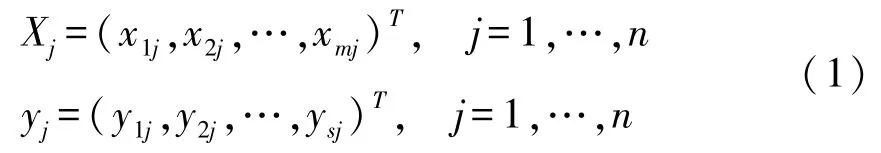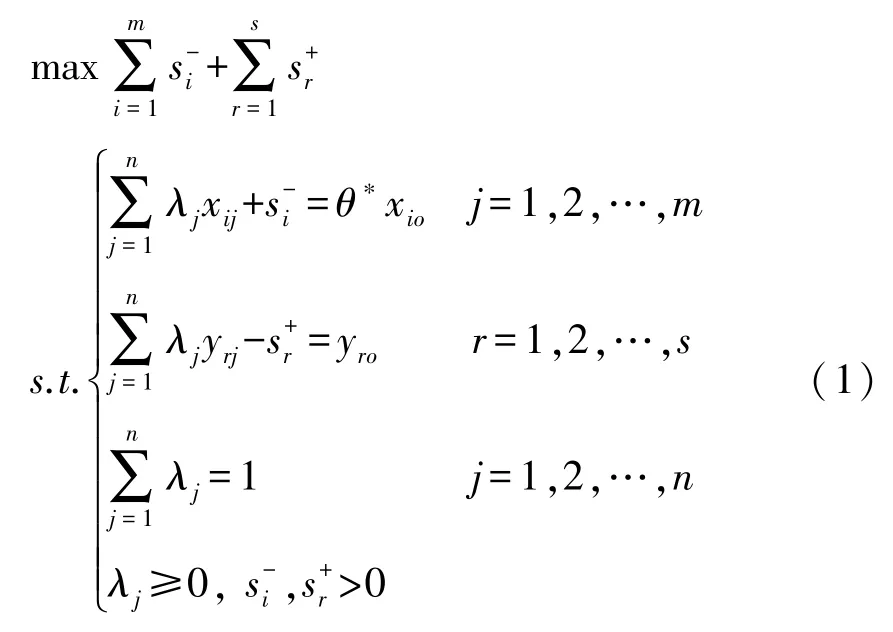粤港澳大湾区工业科技创新效率及其时空演变研究

1（华南师范大学经济与管理学院,广州 510006)

2（仲恺农业工程学院人文与社会科学学院,广州 510225)

具有国家 “世界级城市群”战略定位的粤港澳大湾区依托香港、澳门和广东三地，其吸纳就业、发展经济、整合创新资源、培育创新能力在全国范围内具有领先优势。其工业经济十分发达，2018年工业增加值占国内生产总值比重达21%以上。作为以创新为动力驱动经济发展的重点战略区域，大湾区工业科技创新效率处于何种水平、抑制工业科技创新效率提升的原因有哪些、空间分布情况如何，本文将重点围绕这三大问题展开研究。

科技创新效率是指创新活动中的技术效率。赵传松等［1］筛选出衡量科技创新水平的指标，但并未给出度量科技创新效率的方法。关于科技创新效率度量的方法主要有两种： （1）参数方法，即随机前沿分析 （SFA）； （2）非参数方法，即数据包络分析 （DEA）。 SFA由Aigner等［2］于1977年提出，基本思路是依据随机前沿生产函数扰动项中的技术损失误差项来计算创新主体的技术非效率。目前SFA模型常被用于效率的度量及影响因素分析，如叶祥松和刘敬［3］通过随机前沿模型测算科技创新效率，运用面板门槛模型检验了政府和技术市场发展在科技创新中的作用。余泳泽［4］将科技创新主体分为大学、科研机构和企业，在采用随机前沿分析各创新主体科技创新效率的基础上，运用空间面板计量模型，主要探究创新要素和政府支持对各创新主体科技创新效率的作用。SFA模型只能用于测量具有单一产出的技术效率，对于科技创新活动而言，单一创新产出显然是不现实的，因此大多数学者常用数据包络分析 （DEA）度量科技创新效率。

Charnes等［5］于1978年提出DEA模型，其基本思想是根据多投入指标和多产出指标构成的投入可能性集或生产可能性集，基于距离函数对效率值进行测算，是一种有效的综合评价法。已有学者将DEA方法用于企业、行政区域和产业科技创新效率的评价，熊飞等［6］运用CCR和BCC模型测算科技创新效率，从综合效率、纯技术效率和规模效率3个不同的角度对北京市丰台科技园42家高科技企业进行评价。杜娟和霍佳震［7］认为科技创新是城市创新能力的外在表现，将人才培养输出作为科技创新的人力资源投入，从而构建两阶段DEA模型评价重点城市整体创新能力，并进一步得出子阶段科技创新效率。Wang等［8］选取2009～2013年中国38家能源企业，将科技创新分为研发和市场化，构建两阶段非径向DEA模型研究能源企业科技创新效率。为验证科技创新能否有效驱动经济发展，王慧艳等［9］构建网络WSBM模型对中国各省科技创新促进经济发展绩效水平进行评价。Li等［10］通过三阶段DEA模型测度2009～2014年中国半导体产业的创新效率。Liu等［11］采用K均值聚类法将中国2008～2016年高科技产业分为4类，考虑到环境污染和随机因素的影响，构建SBM-DEA模型测算不同区域的绿色科技创新效率。DEA用于评价具有多投入多产出的决策单元相对效率时，不需要设定具体的生产函数形式，结果更客观、可靠，因而被大多数学者所接受。但DEA方法只能度量相同时期不同决策单元的效率值，结果是静态的，无法对跨期效率的动态变化进行分析。

为了解决这一问题，Fare等［12］将 Malmquist指数应用于效率评价。DEA-Malmquist模型不仅能分析效率的动态变化，还可以进一步探究全要素生产率变动的原因，因此逐渐被学者接受并应用，朱鹏颐等［13］运用超效率DEA视窗模型测算出福建省9个地级市的科技创新效率，进一步联合Malmquist指数考察效率动态变化的原因。晏蒙和孟令杰［14］采用DEA模型和Malmquist指数对中国各省市的工业科技创新效率进行纵横双向对比分析。吴传清等［15］运用DEA-Malmquist模型分析长江经济带科技创新效率，发现上、中、下游效率呈 “V”型分布。郭淑芬和张俊［16］采用DEAMalmquist模型测度中国31个省市的科技创新效率，对冗余情况进行了详细分析。Wang等［17］采用Malmquist-DEA模型测算中国284个城市的能源效率；Luo等［18］以中国战略性新兴产业子行业为研究对象，构建DEA-Malmquist模型将全要素生产率分解为技术效率变化和技术进步，以考察绿色技术创新效率变动的原因。

现有文献丰富了科技创新效率的研究成果，但在研究对象、研究方法等方面也存在一定的不足：（1）以区域城市工业科技创新系统为研究对象的文献较少；（2）在研究方法上，传统的DEA模型只能评价静态的效率，难以分析效率的动态变化；（3）从时空视角来看，现有研究注重时间维度的研究，忽视了研究对象在空间上的变化。

因此，本文以粤港澳大湾区工业科技创新系统为研究对象，采用超效率SBM （Slacks-Based Measure）-Malmquist模型，动静结合揭示科技创新效率变化的深层次原因；运用GIS（Geographic Information System）技术探寻科技创新效率的空间分布规律，更有助于实际问题的解决。

Tone［19］基于松弛变量提出测度效率的SBM模型。与传统DEA模型采用径向投影测度效率且非效率决策单元同比例缩减 （或扩大）投入 （产出）相比，SBM模型采用非径向投影估计效率。对技术有效的决策单元，Tone［19］进一步提出超效率SBM模型进行区分，较传统的DEA模型具有更强的分辨能力。本文假设规模报酬不变，以产出导向的超效率SBM模型测算科技创新效率。

假设有n个决策单元DMUj（x0，y0） （j＝1，2，…，n）， 每个决策单元j有m项投入xij（i＝1，2，…，m），s项产出yrj（r＝1，2，…，s）；X＞0，Y＞0，si、、Aj分别为第j个决策单元的第i项投入松弛、第r项产出松弛以及其影子价格。

2.1.1 SBM 模型［19］

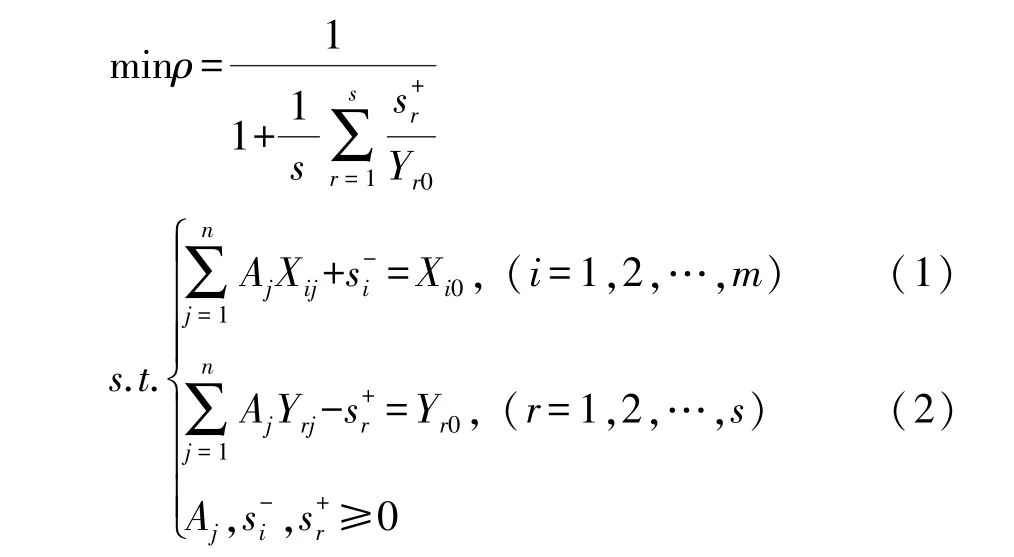
ρ即为所求科技创新效率值，其取值范围：0＜ρ≤1， 式 （1） 表示DMU（x0，y0）实际投入值相对于最优投入存在投入冗余，冗余量为； 式 （2）表示DMU（x0，y0）实际产出相对于最优产出存在产出不足，短缺量为；当时，ρ＝1，DMU（x0，y0）是有效的。对上述模型的求解，可采用Charnes和Cooper［20］的方法转化为线性规划求解。

2.1.2 SBM超效率模型

若上述最优解ρ*＝1的DMU（x0，y0）有多个，SBM模型无法对有效的DMU（x0，y0）进行区分。因此，本文进一步采用 Tone［19］拓展的产出导向SBM模型对超效率部分进行分析，假设决策单元的生产可能性集为P（x0，y0）， 将不包括（x0，y0）的生产可能集定义为P＼（x0，y0）＝｛（，）≥，由于X＞0且Y＞0，非空子集（x0，y0）＝P＼（x0，y0）∩｛≥x0，≤y0｝，基于距离函数的（x0，y0）到（，）∈（x0，y0）的距离即为（x0，y0）的超效率， 记为δ＝

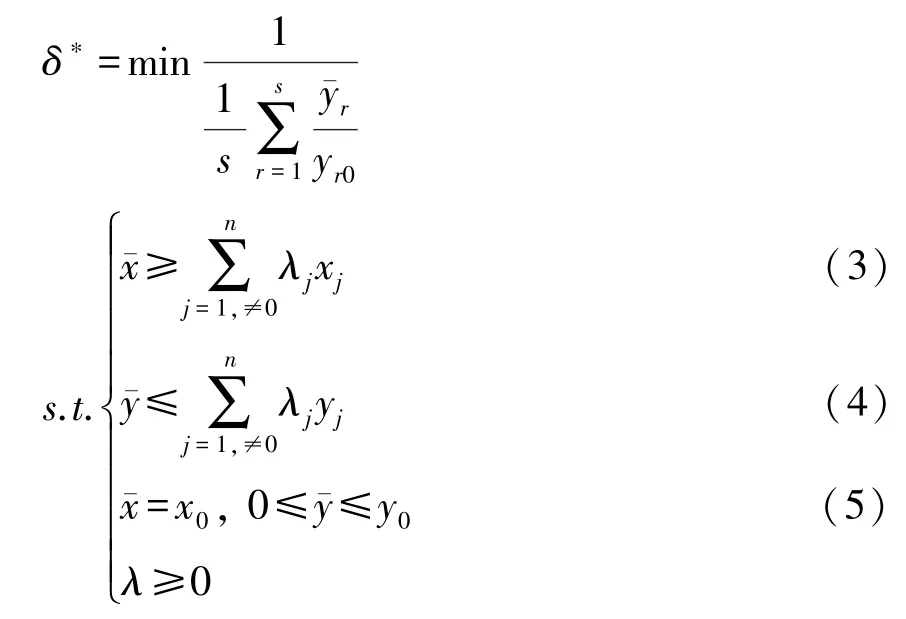
求解方法同上，超效率值δ*≥1，式 （3）和式 （4）表示对生产条件的约束，式 （5）表示从产出角度测算超效率值。

Fare等［12］将Malmquist指数与DEA方法结合，构建DEA-Malmquist模型用于全要素生产率的测算，后被广泛应用。Malmquist指数根据产出距离函数计算生产率的变化，有如下计算公式：

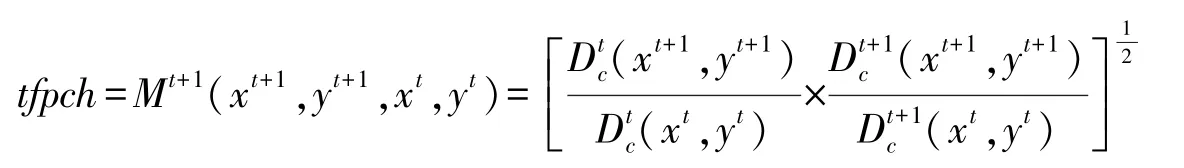
（xt，yt）、 （xt+1，yt+1）分别表示第t期和第t+1期的投入、产出，表示规模报酬不变时，基于第t期 （第t+1期）技术水平来衡量产出效率的距离函数。Mt+1表示从t到t+1期生产率变化程度，Mt+1＞1表示科技创新生产率提高，Mt+1＝1表示科技创新生产率不变，Mt+1＜1表示科技创新生产率下降。Mt+1可以进一步分解为技术效率指数 （effch）和技术进步指数 （techch），计算公式为：

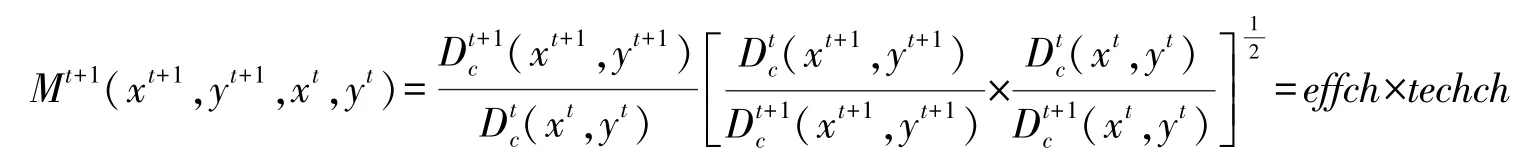
当规模报酬可变时，技术效率指数 （effch）又可以进一步分解为纯技术效率指数 （pech）和规模指数 （sech），计算公式如下：

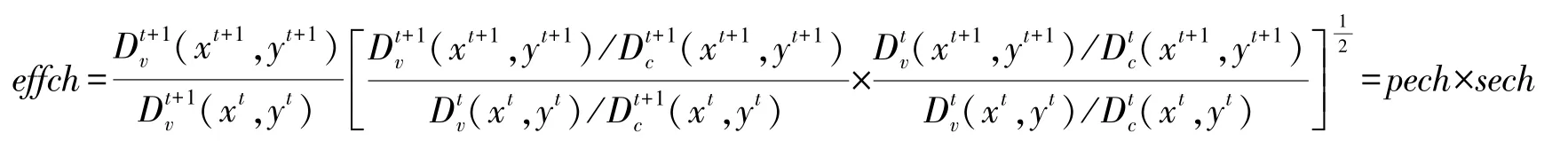
最终，科技创新生产率计算公式：

tfpch＝techch×pech×sech

科技创新系统是一项多投入、多产出的复杂生产活动，根据生产理论，在现有技术水平下，科技创新生产过程需要劳动要素和资本要素的投入，科技成果的产出由劳动投入量、资本投入量和技术水平共同决定。如郭淑芬和张俊［16］在评价中国31省的整体科技创新效率时，从劳动、资本和技术水平3个方面选取投入指标；在短期，技术进步来不及实现，因此通常技术水平保持不变，朱鹏颐等［13］、 吴传清等［15］从劳动和资本两方面选取科技创新投入指标，从科技活动的中间产出和最终产出过程选取产出指标。科技创新效率反映的是科技产出与科技投入之间的关系，因此，投入产出指标的选取直接关系到研究结果的可靠性。

本文在现有研究的基础上，从投入产出角度，谨慎地借鉴吴传清等［15］学者的评价指标，科技劳动要素投入选取规模以上工业企业R＆D活动人员指标，科技资本要素选取规模以上工业企业R＆D经费内部支出作为投入指标；科技创新产出包括直接产出和间接产出，选取专利申请授权量作为科技创新直接产出指标，直接反映科技研发人员的知识转化成果，从最终产品市场化获得经济效益的角度，间接产出选取规模以上工业企业新产品销售收入和规模以上工业增加值反映工业科技创新活动市场化产出成果，如表1所示。

表1 工业企业科技创新效率投入产出指标

本文以粤港澳大湾区10个城市的工业企业为研究对象 （澳门经济发展主要是由以博彩业为主的服务业带动，工业占比极小，可忽略不计，故从研究样本中剔除），考虑到科技创新活动投入产出具有一定的时滞性，根据现有研究成果，将滞后期定为1年，即投入指标时间为2010～2017年，产出指标为2011～2018年，所有数据来源于《广东统计年鉴》、《广东科技年鉴》、《香港统计年刊》及各地市统计公报。其中，规模以上工业企业R＆D经费内部支出指标以2010年为基期，采用研发价格指数［13］进行平减得到，规模以上工业企业新产品销售收入和规模以上工业增加值指标也以2010年为基期，采用工业生产者出厂价格指数 （PPI）进行平减，将可变价格转换成可比价格以消除通货膨胀等价格波动的影响。

4.2.1 科技创新效率分析

本文基于粤港澳大湾区2010～2018年科技创新投入指标和产出指标的面板数据，求解上述SBM模型和SBM超效率模型，分别解出小于1和大于1的效率值，将结果汇总得到粤港澳大湾区各城市科技创新效率值，如表2所示。

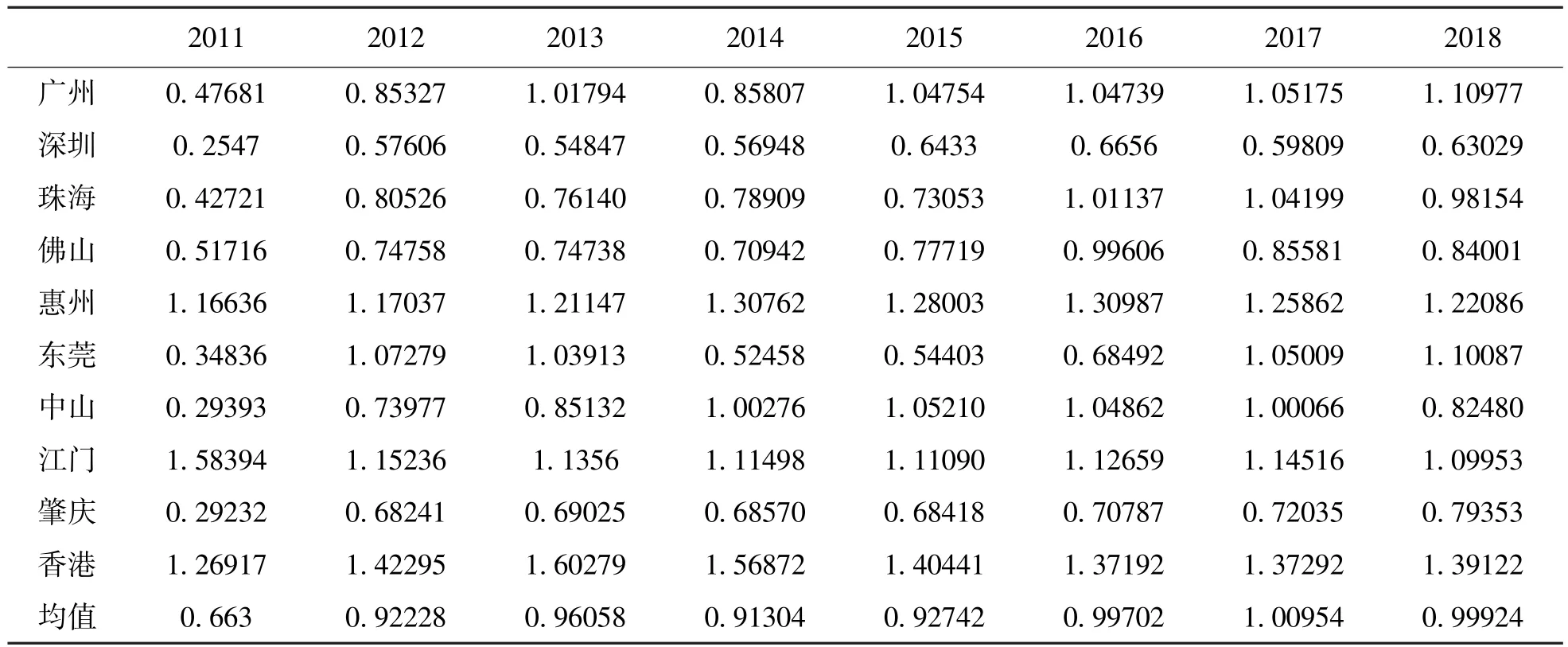
表2 2011～2018年粤港澳大湾区工业科技创新效率

由表2可知，科技创新效率均值呈波动上升趋势，这表明粤港澳大湾区整体科技创新活动资源利用能力处于提高状态，但大湾区内各城市科技创新效率存在较大差距。香港、惠州、江门3个城市产出完全有效，且香港科技创新效率值最大、惠州次之、江门最低，表明香港具有较强的科技资源转化能力，重视产品研发和技术应用，这与创新型城市的定位相符，惠州和江门的资源投入规模一般，却表现出产出有效，说明其科技创新系统规模较小，创新体制机制完善、技术管理水平较佳，对新技术能较好的吸收转化。另外，深圳、佛山和肇庆3个城市产出虽完全无效，效率值却缓慢提升，值得注意的是，深圳有多家高科技企业，科技产出较其他城市应该具有领先优势，但科技创新效率却表现不佳。广州、珠海、东莞和中山4个城市产出有效状态不稳定，4个城市有可能处于调整阶段。

4.2.2 基于Malmquist指数的动态分析

运用Malmquist指数对粤港澳大湾区各城市科技创新效率进行全要素生产率分解，进一步挖掘科技创新效率变化的深层次原因。各城市的Malmquist指数及其分解结果，如表3所示。

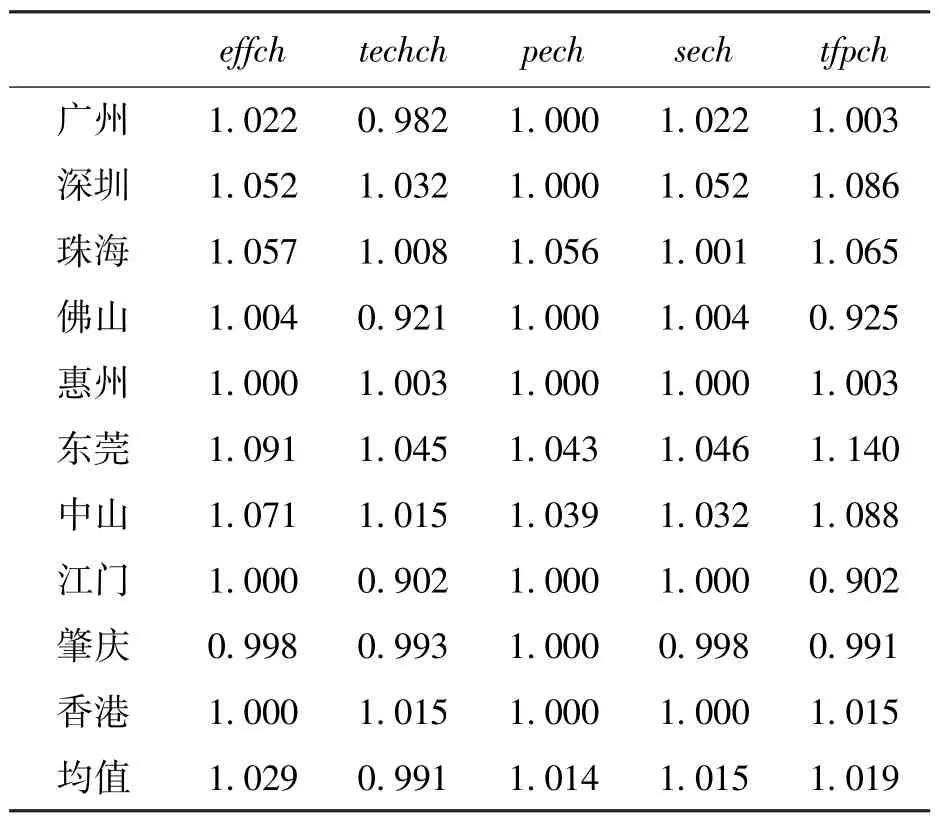
表3 2011～2018年粤港澳大湾区工业科技创新平均Malmquist指数

由表3可知，2011～2018年粤港澳大湾区各城市科技创新全要素生产率 （tfpch）区域差异较大，大多数城市的tfpch呈上升趋势，年均上升了1.9%。从Malmquist指数的分解效率来看，全要素生产率的上升是技术效率指数 （effch）促进的结果，技术效率指数年均提升了2.9%，其上升是纯技术效率 （pech）和规模效率 （sech）共同作用的结果，分别上升了1.4%和1.5%，这表明各城市不仅注重科技创新组织内部创新制度的完善和管理水平的提升，而且加强了外部科技创新资源投入。技术进步指数年均降低了0.9%，技术进步是抑制全要素生产率提升的主要因素。

从总体来看，大湾区有7个城市工业科技创新生产率呈上升趋势，上升幅度最大的是东莞，tfpch提升了14%，其次是中山，tfpch提升了8.8%。在这7个城市中，工业科技创新生产率的提升主要源于3个方面：（1）技术效率指数和技术进步指数共同驱动，有深圳、珠海、东莞和中山4个城市；值得注意的是，东莞的全要素生产率不仅在这4个城市中表现较佳，而且是大湾区城市中效率提升最大的城市，tfpch上升了14%，技术效率指数和技术进步指数分别上升了9.1%和4.5%，纯技术效率提高了4.3%，规模效率提高了4.6%，说明东莞具有较好的工业发展基础，另外，无论是在组织架构、内部管理、企业规模还是技术创新方面的先进经验，都值得其他城市的工业企业学习、借鉴；（2）技术效率指数促进，技术进步指数抑制，只有广州；广州的规模效率提升了2.2%，说明工业企业内部结构的调整使企业逐渐处于递增规模，引起的技术效率提升效应大于技术发展停滞带来的不利影响，最终使全要素生产率得以提升；（3）技术效率指数不变，技术进步指数促进，包括香港和惠州；香港的技术进步指数上升了1.5%，其他指数均为1，说明香港在其他方面经验丰富，已无提升空间，只有通过R＆D创新这一途径，才能提高全要素生产率；惠州的技术进步指数上升了0.3%，表明惠州在技术创新方面具有发展潜力。

另外，佛山、江门、肇庆三个城市的工业科技创新生产率呈下降趋势，导致下降的原因包括3个方面：（1）技术效率指数无影响，技术进步指数抑制，如江门；（2）技术效率指数和技术进步指数共同抑制了全要素生产率的提升，如肇庆；（3）技术效率指数促进，技术进步指数抑制，只有佛山。从表3可以看出，技术进步是抑制佛山、江门和肇庆全要素生产率提升的关键因素，技术进步指数分别下降7.9%、9.8%、0.7%，因此，提高R＆D创新能力是改善全要素生产率的有效途径。

4.2.3 科技创新效率时空演变

从时空视角来看，本文分别选取2011年、2013年、2015年和2018年作为时间节点，采用Arc-GIS绘图软件里的自然间断法，将由超效率SBM模型得到的科技创新综合效率分为5类。利用ArcGIS 10.5绘制出科技创新效率的时空演变图（图1），从时间序列来看，大湾区整体的科技创新效率不断提高；从空间分布来看，科技创新效率高的地区向东部和中部集中，西部效率低但处于追赶阶段，深圳效率最低。

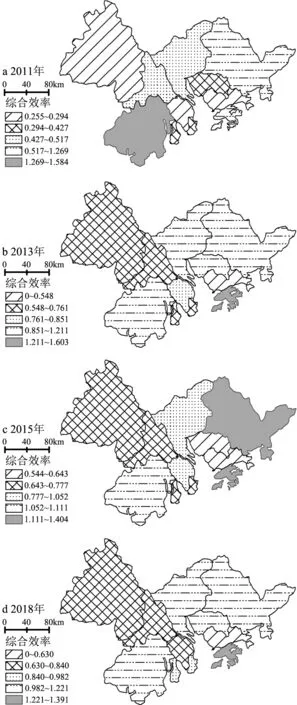
图1 粤港澳大湾区工业科技创新效率分布格局

从2011年科技创新效率分布的五大区域来看，以广州为中心，大湾区东部和西南部的科技创新效率表现较好，中部、西部和东南地区具有一定差异，其中西部和东南地区效率较低。2013年中部和西部的效率得到提高，东南地区内部差异较大，香港科技创新效率较高，深圳最低。到2015年，大湾区东部科技创新效率进一步提高，中部地区存在波动，2018年大湾区工业科技创新效率空间分布格局基本形成，西部和南部效率低，西南和东部效率高，东南地区差异明显，深圳最低。

有关科技创新效率的研究中，评价指标和评价模型的选取对研究结果具有十分重要的影响。在模型的选择上，随机前沿分析需要假设生产函数的具体形式，存在函数形式的设定误差，影响结果的可信度，因而DEA模型常被用于评价科技创新效率。传统的DEA模型在提高非有效单元科技创新效率时，采用径向的方法对投入或产出进行调整，灵活度较低；SBM模型基于松弛变量测算科技创新效率，可以非径向调整非有效单元的投入或产出，但对有效单元无法进行区分，在这种情况下，超效率SBM模型被提出。超效率SBM模型无法分析科技创新效率的动态变化，更不能探究其空间分布及演变过程。

为了解决上述问题，本文以粤港澳大湾区工业科技创新系统为研究对象，运用超效率SBM模型评价2011～2018年各城市工业科技创新系统的相对有效性。从动态视角联合Malmquist指数分析科技创新效率的变化，并将科技创新生产率进一步分解为技术效率指数和技术进步指数，深挖抑制大湾区工业科技创新生产率提升的原因。随后，从空间维度采用GIS技术研究科技创新综合效率的空间分布及其变化规律。研究发现： （1）工业科技创新有效城市占比增大，非有效城市效率值逐渐增大，整体上，大湾区工业科技创新系统呈优化提升状态； （2）技术效率上升使广州、深圳、珠海、东莞、中山5个城市的全要素生产率得以提高，技术进步制约是江门、肇庆和佛山科技创新生产率下降的主要原因；（3）从空间分布格局来看，同一类工业科技创新效率逐渐呈现连片化趋势，大湾区东部效率明显优于西部。